Cómo aumentar la precisión de una red neuronal de capa oculta

En este artículo, realizaremos algunos experimentos de clasificación y recopilaremos datos sobre la relación entre la dimensionalidad de la capa oculta y el rendimiento de la red.

En este artículo, aprenderá a modificar una capa oculta para mejorar la precisión de la red neuronal mediante una implementación de Python y problemas de ejemplo.

Sin embargo, antes de pasar a ese tema, considere ponerse al día con las entradas anteriores de esta serie sobre redes neuronales:

1. Cómo realizar la clasificación mediante una red neuronal:¿Qué es el perceptrón?
2. Cómo utilizar un ejemplo de red neuronal de Perceptron simple para clasificar datos
3. Cómo entrenar una red neuronal de perceptrón básica
4. Comprensión del entrenamiento de redes neuronales simples
5. Introducción a la teoría del entrenamiento para redes neuronales
6. Comprensión de la tasa de aprendizaje en redes neuronales
7. Aprendizaje automático avanzado con el perceptrón multicapa
8. La función de activación sigmoidea:activación en redes neuronales de perceptrones multicapa
9. Cómo entrenar una red neuronal de perceptrón multicapa
10. Comprender las fórmulas de entrenamiento y la retropropagación para perceptrones multicapa
11. Arquitectura de red neuronal para una implementación de Python
12. Cómo crear una red neuronal de perceptrón multicapa en Python
13. Procesamiento de señales mediante redes neuronales:validación en el diseño de redes neuronales
14. Conjuntos de datos de entrenamiento para redes neuronales:cómo entrenar y validar una red neuronal Python
15. ¿Cuántas capas y nodos ocultos necesita una red neuronal?
16. Cómo aumentar la precisión de una red neuronal de capa oculta

El número de nodos incluidos en una capa oculta influye en la capacidad de clasificación y la velocidad de una red neuronal Perceptron. Vamos a realizar experimentos que nos ayudarán a formular una intuición incipiente sobre cómo encaja la dimensionalidad de la capa oculta en el intento de diseñar una red que entrene en un período de tiempo razonable, produzca valores de salida con una latencia aceptable y cumpla con los requisitos de precisión. .

Evaluación comparativa en Python

El código Python de la red neuronal presentado en la Parte 12 ya incluye una sección que calcula la precisión mediante el uso de la red entrenada para clasificar muestras de un conjunto de datos de validación. Por lo tanto, todo lo que tenemos que hacer es agregar un código que informará el tiempo de ejecución para el entrenamiento (que incluye la operación de retroalimentación y la propagación hacia atrás) y para la funcionalidad de clasificación real (que incluye solo la operación de retroalimentación). Usaremos time.perf_counter () función para esto.

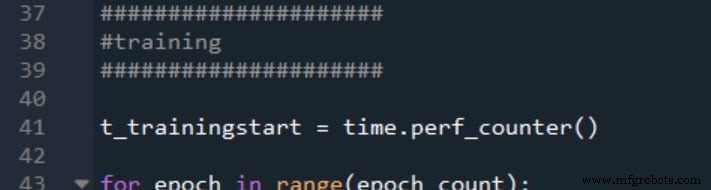
Así es como marco el inicio y el final de la formación:

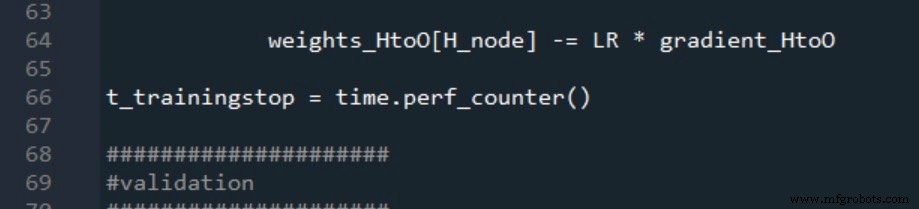
Los tiempos de inicio y finalización de la validación se generan de la misma manera:

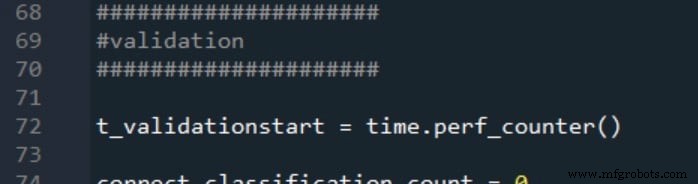
Las dos mediciones del tiempo de procesamiento se informan de la siguiente manera:

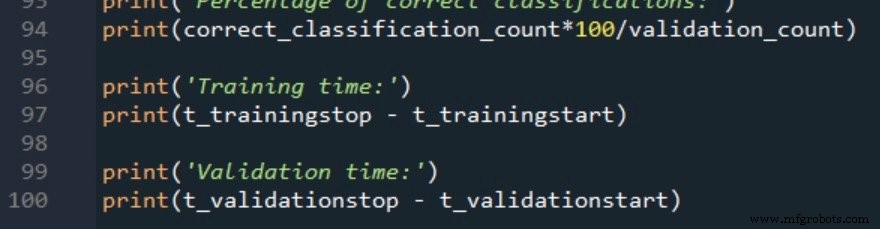
Procedimiento de medición y datos de entrenamiento

La red neuronal realizará una clasificación de verdadero / falso en muestras de entrada que constan de cuatro valores numéricos entre –20 y +20.

Por lo tanto, tenemos cuatro nodos de entrada y un nodo de salida, y los valores de entrada se generan con la ecuación de Excel que se muestra a continuación.

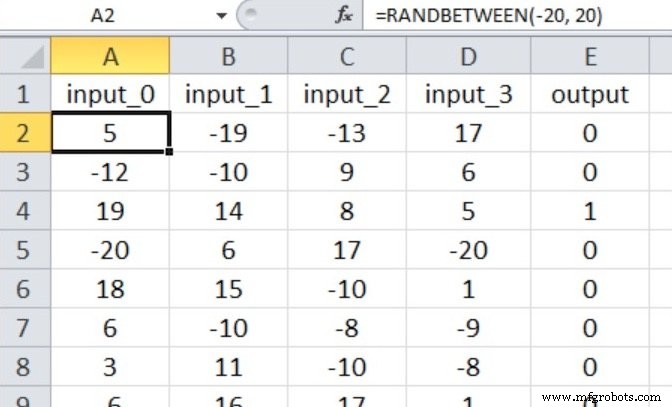
Mi conjunto de datos de entrenamiento consta de 40.000 muestras y el conjunto de validación tiene 5000 muestras. La tasa de aprendizaje es de 0,1 y estoy realizando solo una época de entrenamiento.

Realizaremos tres experimentos que representan las relaciones de entrada y salida con diversos grados de complejidad. La np.random.seed (1) La declaración está comentada, por lo que los valores de peso iniciales variarán y, por lo tanto, también lo hará la precisión de la clasificación.

En cada experimento, el programa se ejecutará cinco veces (con los mismos datos de entrenamiento y validación) para cada dimensionalidad de capa oculta, y las mediciones finales de precisión y tiempo de procesamiento serán la media aritmética de los resultados generados por las cinco ejecuciones separadas. .

Experimento 1:un problema de baja complejidad

En este experimento, la salida es verdadera solo si las primeras tres entradas son mayores que cero, como se muestra en la captura de pantalla de Excel a continuación (tenga en cuenta que la cuarta entrada no tiene ningún efecto en el valor de salida).

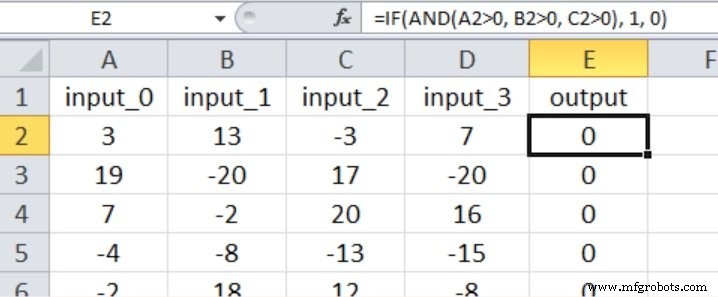
Creo que esto califica como una relación entrada-salida bastante simple para un perceptrón multicapa.

Basado en las recomendaciones que proporcioné en la Parte 15 con respecto a cuántas capas y nodos necesita una red neuronal, comenzaría con una dimensionalidad de capa oculta igual a dos tercios de la dimensionalidad de entrada.

Como no puedo tener una capa oculta con una fracción de un nodo, comenzaré en H_dim =2 . La siguiente tabla presenta los resultados.

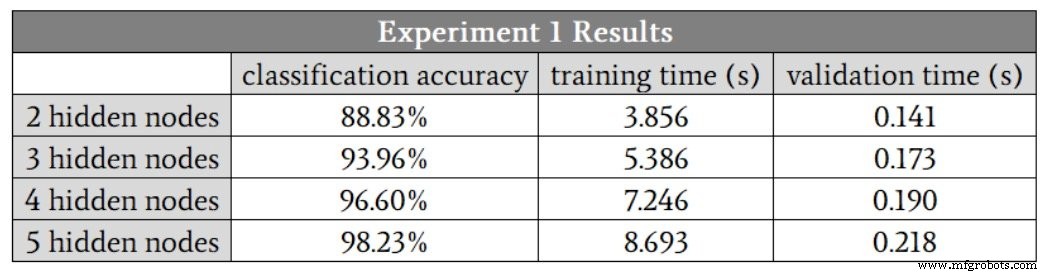
Vemos una mejora en la clasificación hasta cinco nodos ocultos. Sin embargo, creo que estos números exageran el beneficio de aumentar de cuatro a cinco nodos, porque la precisión de una de las ejecuciones de cuatro nodos ocultos fue del 88,6%, y esto redujo el promedio.

Si elimino esa ejecución de baja precisión, la precisión promedio de cuatro nodos ocultos es en realidad un poco más alta que el promedio de cinco nodos ocultos. Sospecho que en este caso, cuatro nodos ocultos proporcionarán el mejor equilibrio entre precisión y velocidad.

Otra cosa importante a notar en estos resultados es la diferencia en cómo la dimensionalidad de la capa oculta afecta el tiempo de entrenamiento y el tiempo de procesamiento. Pasar de dos a cuatro nodos ocultos aumenta el tiempo de validación en un factor de 1,3, pero aumenta el tiempo de entrenamiento en un factor de 1,9.

El entrenamiento es significativamente más intensivo desde el punto de vista computacional que el procesamiento anticipado, por lo que debemos ser particularmente conscientes de cómo la configuración de la red influye en nuestra capacidad para entrenar la red en un período de tiempo razonable.

Experimento 2:un problema de complejidad moderada

La captura de pantalla de Excel muestra la relación entrada-salida para este experimento. Las cuatro entradas ahora influyen en el valor de salida y las comparaciones son menos sencillas que en el Experimento 1.

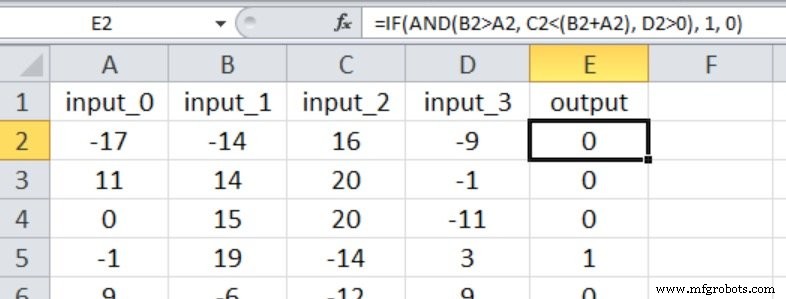
Empecé con tres nodos ocultos. Estos son los resultados:

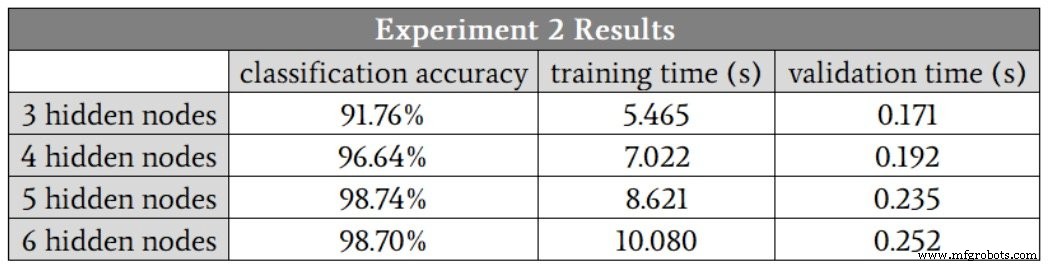
En este caso, sospecho que cinco nodos ocultos nos darán la mejor combinación de precisión y velocidad, aunque una vez más, las ejecuciones de cuatro nodos ocultos produjeron un valor de precisión que fue significativamente más bajo que los demás. Si ignora este valor atípico, los resultados para cuatro nodos ocultos, cinco nodos ocultos y seis nodos ocultos se verán muy similares.

El hecho de que las ejecuciones de cinco nodos ocultos y seis nodos ocultos no generaron ningún valor atípico nos lleva a un posible hallazgo interesante:tal vez aumentar la dimensionalidad de la capa oculta hace que la red sea más robusta frente a condiciones que, por alguna razón, hacen que el entrenamiento se deteriore. ser particularmente difícil.

Experimento 3:un problema de alta complejidad

Como se muestra a continuación, la nueva relación entrada-salida incluye nuevamente los cuatro valores de entrada, y hemos introducido la no linealidad elevando al cuadrado una de las entradas y tomando la raíz cuadrada de otra.

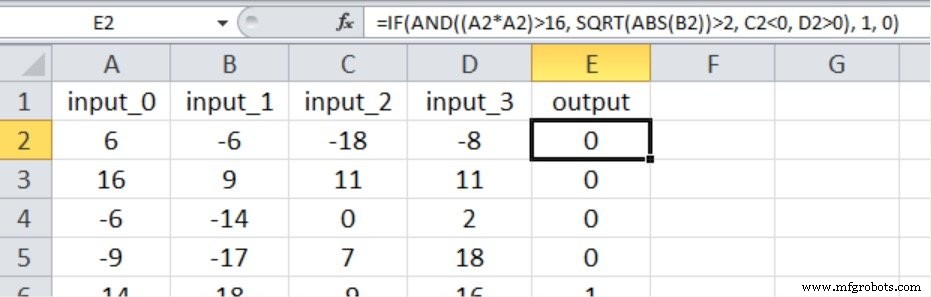
Estos son los resultados:

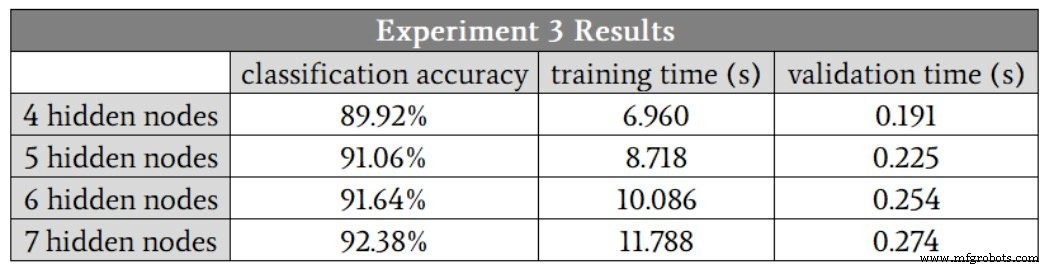
La red definitivamente tuvo más dificultades con esta relación matemática de mayor complejidad; incluso con siete nodos ocultos, la precisión fue menor que la que logramos con solo tres nodos ocultos en el problema de baja complejidad. Estoy seguro de que podríamos mejorar el rendimiento de alta complejidad modificando otros aspectos de la red, por ejemplo, incluyendo un sesgo (consulte la Parte 11) o recociendo la tasa de aprendizaje (consulte la Parte 6).

Sin embargo, mantendría la dimensionalidad de la capa oculta en siete hasta que estuviera completamente convencido de que otras mejoras podrían permitir que la red mantuviera un rendimiento adecuado con una capa oculta más pequeña.

Conclusión

Hemos visto algunas mediciones interesantes que pintan una imagen bastante clara de la relación entre la dimensionalidad de la capa oculta y el rendimiento del Perceptron. Ciertamente, hay muchos más detalles que podríamos explorar, pero creo que esto le brinda información fundamental sólida a la que puede recurrir cuando experimente con el diseño y la capacitación de redes neuronales.