Cómo entrenar una red neuronal de perceptrón básico

Este artículo presenta código Python que le permite generar pesos automáticamente para una red neuronal simple.

Bienvenido a la serie de AAC sobre redes neuronales Perceptron. Si desea comenzar desde el principio para obtener antecedentes o avanzar, consulte el resto de los artículos aquí:

1. Cómo realizar la clasificación mediante una red neuronal:¿Qué es el perceptrón?
2. Cómo utilizar un ejemplo de red neuronal de Perceptron simple para clasificar datos
3. Cómo entrenar una red neuronal de perceptrón básica
4. Comprensión del entrenamiento de redes neuronales simples
5. Introducción a la teoría del entrenamiento para redes neuronales
6. Comprensión de la tasa de aprendizaje en redes neuronales
7. Aprendizaje automático avanzado con el perceptrón multicapa
8. La función de activación sigmoidea:activación en redes neuronales de perceptrones multicapa
9. Cómo entrenar una red neuronal de perceptrón multicapa
10. Comprender las fórmulas de entrenamiento y la retropropagación para perceptrones multicapa
11. Arquitectura de red neuronal para una implementación de Python
12. Cómo crear una red neuronal de perceptrón multicapa en Python
13. Procesamiento de señales mediante redes neuronales:validación en el diseño de redes neuronales
14. Conjuntos de datos de entrenamiento para redes neuronales:cómo entrenar y validar una red neuronal Python

Clasificación con un perceptrón de capa única

El artículo anterior introdujo una tarea de clasificación sencilla que examinamos desde la perspectiva del procesamiento de señales basado en redes neuronales. La relación matemática requerida para esta tarea fue tan simple que pude diseñar la red con solo pensar en cómo un cierto conjunto de pesos permitiría que el nodo de salida categorizara correctamente los datos de entrada.

Esta es la red que diseñé:

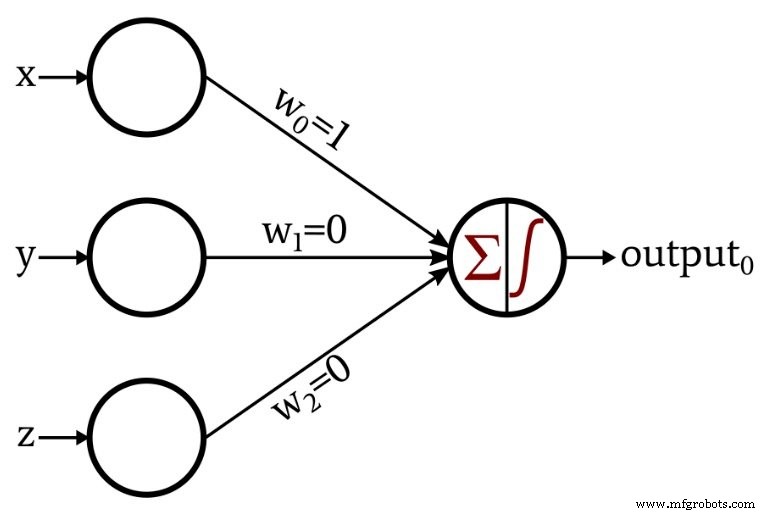
La función de activación en el nodo de salida es el paso unitario:

\ [f (x) =\ begin {cases} 0 &x <0 \\ 1 &x \ geq 0 \ end {cases} \]

La discusión se volvió un poco más interesante cuando presenté una red que creaba sus propios pesos a través del procedimiento conocido como entrenamiento:

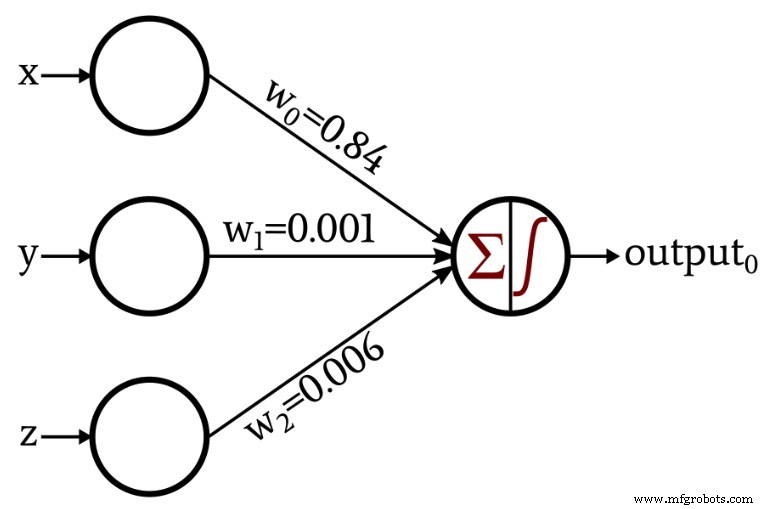
En el resto de este artículo, examinaremos el código Python que utilicé para obtener estos pesos.

Una red neuronal Python

Aquí está el código:

 importar pandas importar numpy como np input_dim =3 tasa_de_aprendizaje =0.01 Pesos =np.random.rand (input_dim) #Weights [0] =0.5 #Weights [1] =0.5 #Weights [2] =0.5 Training_Data =pandas.read_excel ("3D_data.xlsx") Expected_Output =Training_Data.output Training_Data =Training_Data.drop (['salida'], eje =1) Training_Data =np.asarray (Training_Data) training_count =len (Training_Data [:, 0]) para la época en el rango (0,5):para datum en rango (0, training_count):Output_Sum =np.sum (np.multiply (Training_Data [datum ,:], Weights)) si Output_Sum <0:Output_Value =0 demás:Output_Value =1 error =Expected_Output [datum] - Output_Value para n en el rango (0, input_dim):Weights [n] =Weights [n] + learning_rate * error * Training_Data [datum, n] print ("w_0 =% .3f"% (Pesos [0])) print ("w_1 =% .3f"% (Pesos [1])) print ("w_2 =% .3f"% (Pesos [2])) 

Echemos un vistazo más de cerca a estas instrucciones.

Configuración de la red y organización de datos

 input_dim =3 

La dimensionalidad es ajustable. Nuestros datos de entrada, si recuerda, constan de coordenadas tridimensionales, por lo que necesitamos tres nodos de entrada. Este programa no admite varios nodos de salida, pero incorporaremos la dimensionalidad de salida ajustable en un experimento futuro.

 tasa_de_aprendizaje =0.01 

Hablaremos de la tasa de aprendizaje en un artículo futuro.

 Pesos =np.random.rand (input_dim) #Weights [0] =0.5 #Weights [1] =0.5 #Weights [2] =0.5 

Normalmente, los pesos se inicializan a valores aleatorios. La función numpy random.rand () genera una matriz de longitud input_dim poblado con valores aleatorios distribuidos en el intervalo [0, 1). Sin embargo, los valores de peso iniciales influyen en los valores de peso final producidos por el procedimiento de entrenamiento, por lo que si desea evaluar los efectos de otras variables (como el tamaño del conjunto de entrenamiento o la tasa de aprendizaje), puede eliminar este factor de confusión configurando todos los pesos a una constante conocida en lugar de un número generado aleatoriamente.

 Training_Data =pandas.read_excel ("3D_data.xlsx") 

Utilizo la biblioteca de pandas para importar datos de entrenamiento desde una hoja de cálculo de Excel. El próximo artículo entrará en más detalles sobre los datos de entrenamiento.

 Expected_Output =Training_Data.output Training_Data =Training_Data.drop (['salida'], eje =1) 

El conjunto de datos de entrenamiento incluye valores de entrada y valores de salida correspondientes. La primera instrucción separa los valores de salida y los almacena en una matriz separada, y la siguiente instrucción elimina los valores de salida del conjunto de datos de entrenamiento.

 Training_Data =np.asarray (Training_Data) training_count =len (Training_Data [:, 0]) 

Convierto el conjunto de datos de entrenamiento, que actualmente es una estructura de datos de pandas, en una matriz numerosa y luego miro la longitud de una de las columnas para determinar cuántos puntos de datos están disponibles para el entrenamiento.

Cálculo de valores de salida

 para época en el rango (0,5):

La duración de una sesión de entrenamiento se rige por la cantidad de datos de entrenamiento disponibles. Sin embargo, puede continuar optimizando los pesos entrenando la red varias veces usando el mismo conjunto de datos; los beneficios del entrenamiento no desaparecen simplemente porque la red ya ha visto estos datos de entrenamiento. Cada pasada completa a través de todo el conjunto de entrenamiento se denomina época.

 para datum en rango (0, training_count):

El procedimiento contenido en este ciclo ocurre una vez para cada fila en el conjunto de entrenamiento, donde "fila" se refiere a un grupo de valores de datos de entrada y el valor de salida correspondiente (en nuestro caso, un grupo de entrada consta de tres números que representan x, y y componentes z de un punto en el espacio tridimensional).

 Output_Sum =np.sum (np.multiply (Training_Data [datum ,:], Weights)) 

El nodo de salida debe sumar los valores entregados por los tres nodos de entrada. Mi implementación de Python hace esto al realizar primero una multiplicación por elementos de la matriz Training_Data y los pesos matriz y luego calcular la suma de los elementos en la matriz producida por esa multiplicación.

 si Output_Sum <0:Output_Value =0 demás:Output_Value =1 

Una declaración if-else aplica la función de activación de paso unitario:si la suma es menor que cero, el valor generado por el nodo de salida es 0; si la suma es igual o mayor que cero, el valor de salida es uno.

Actualización de pesos

Cuando se completa el primer cálculo de salida, tenemos valores de peso, pero no nos ayudan a lograr la clasificación porque se generan de forma aleatoria. Convertimos la red neuronal en un sistema de clasificación eficaz modificando repetidamente los pesos de modo que reflejen gradualmente la relación matemática entre los datos de entrada y los valores de salida deseados. La modificación del peso se logra aplicando la siguiente regla de aprendizaje para cada fila del conjunto de entrenamiento:

\ [w_ {new} =w + (\ alpha \ times (salida_ {esperada} -salida_ {calculada}) \ veces entrada) \]

El símbolo \ (\ alpha \) denota la tasa de aprendizaje. Por lo tanto, para calcular un nuevo valor de peso, multiplicamos el valor de entrada correspondiente por la tasa de aprendizaje y por la diferencia entre la salida esperada (que es proporcionada por el conjunto de entrenamiento) y la salida calculada, y luego se suma el resultado de esta multiplicación. al valor de peso actual. Si definimos delta ( \ (\ delta \) ) como (\ (salida_ {esperado} - salida_ {calculado} \)), podemos reescribir esto como

\ [w_ {new} =w + (\ alpha \ times \ delta \ times input) \]

Así es como implementé la regla de aprendizaje en Python:

 error =Expected_Output [datum] - Output_Value para n en el rango (0, input_dim):Weights [n] =Weights [n] + learning_rate * error * Training_Data [datum, n] 

Conclusión

Ahora tiene un código que puede usar para entrenar un perceptrón de una sola capa y un solo nodo de salida. Exploraremos más detalles sobre la teoría y la práctica del entrenamiento de redes neuronales en el próximo artículo.