Comprender los mínimos locales en el entrenamiento de redes neuronales

Este artículo analiza una complicación que puede evitar que su Perceptron logre una precisión de clasificación adecuada.

En la serie de redes neuronales AAC, hemos cubierto una amplia gama de temas relacionados con la comprensión y el desarrollo de redes neuronales de Perceptron multicapa. Antes de leer este artículo sobre mínimos locales, póngase al día con el resto de la serie a continuación:

1. Cómo realizar la clasificación mediante una red neuronal:¿Qué es el perceptrón?
2. Cómo utilizar un ejemplo de red neuronal de Perceptron simple para clasificar datos
3. Cómo entrenar una red neuronal de perceptrón básica
4. Comprensión del entrenamiento de redes neuronales simples
5. Introducción a la teoría del entrenamiento para redes neuronales
6. Comprensión de la tasa de aprendizaje en redes neuronales
7. Aprendizaje automático avanzado con el perceptrón multicapa
8. La función de activación sigmoidea:activación en redes neuronales de perceptrones multicapa
9. Cómo entrenar una red neuronal de perceptrón multicapa
10. Comprender las fórmulas de entrenamiento y la retropropagación para perceptrones multicapa
11. Arquitectura de red neuronal para una implementación de Python
12. Cómo crear una red neuronal de perceptrón multicapa en Python
13. Procesamiento de señales mediante redes neuronales:validación en el diseño de redes neuronales
14. Conjuntos de datos de entrenamiento para redes neuronales:cómo entrenar y validar una red neuronal Python
15. ¿Cuántas capas y nodos ocultos necesita una red neuronal?
16. Cómo aumentar la precisión de una red neuronal de capa oculta
17. Incorporación de nodos de sesgo en su red neuronal
18. Comprensión de los mínimos locales en el entrenamiento de redes neuronales

El entrenamiento de redes neuronales es un proceso complejo. Afortunadamente, no tenemos que entenderlo perfectamente para beneficiarnos de él:las arquitecturas de red y los procedimientos de capacitación que utilizamos realmente dan como resultado sistemas funcionales que logran una precisión de clasificación muy alta. Sin embargo, hay un aspecto teórico de la formación que, a pesar de ser algo abstruso, merece nuestra atención.

Lo llamaremos "el problema de los mínimos locales".

¿Por qué los mínimos locales merecen nuestra atención?

Bueno, no estoy seguro. Cuando aprendí por primera vez sobre las redes neuronales, me quedé con la impresión de que los mínimos locales son realmente un obstáculo importante para el éxito del entrenamiento, al menos cuando nos enfrentamos a relaciones complejas de entrada y salida. Sin embargo, creo que las investigaciones recientes están minimizando la importancia de los mínimos locales. Quizás las estructuras de red y las técnicas de procesamiento más nuevas han mitigado la gravedad del problema, o quizás simplemente tenemos una mejor comprensión de cómo las redes neuronales realmente navegan hacia la solución deseada.

Revisaremos el estado actual de los mínimos locales al final de este artículo. Por ahora, responderé mi pregunta de la siguiente manera:los mínimos locales merecen nuestra atención porque, primero, nos ayudan a pensar más profundamente sobre lo que realmente está sucediendo cuando entrenamos una red a través del descenso de gradiente, y segundo, porque los mínimos locales son:o al menos fueron —Considerado como un impedimento significativo para la implementación exitosa de redes neuronales en sistemas de la vida real.

¿Qué es un mínimo local?

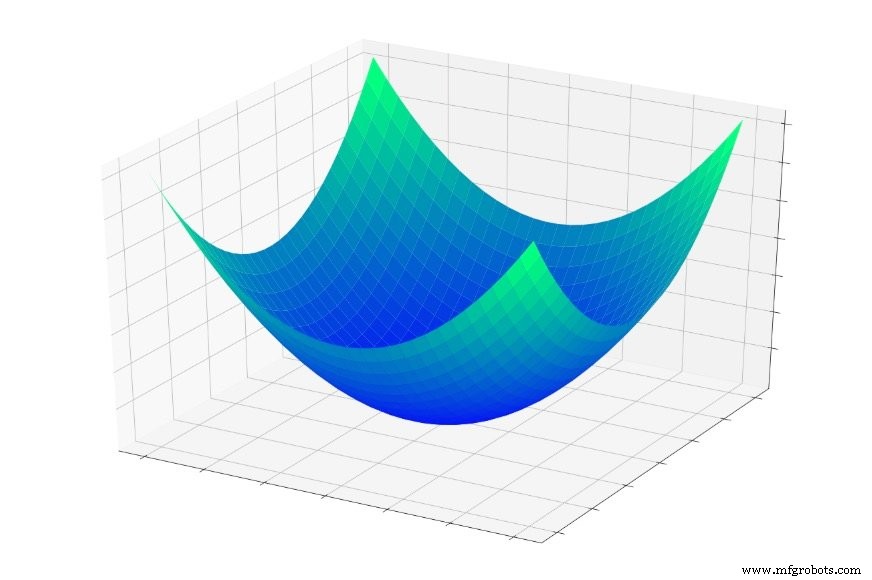
En la Parte 5, consideramos el "tazón de error" que se muestra a continuación, y describí el entrenamiento como esencialmente una búsqueda del punto más bajo en este tazón.

( Nota :A lo largo de este artículo, mis imágenes y explicaciones se basarán en nuestra comprensión intuitiva de las estructuras tridimensionales, pero tenga en cuenta que los conceptos generales no se limitan a las relaciones tridimensionales. De hecho, con frecuencia usamos redes neuronales cuya dimensionalidad excede con mucho dos variables de entrada y una variable de salida.)

Si tuvieras que saltar a este cuenco, te deslizarías hasta el fondo, todo el tiempo. No importa por dónde empiece , terminará en el punto más bajo de toda la función de error. Este punto más bajo es el mínimo global . Cuando una red ha convergido en el mínimo global, ha optimizado su capacidad para clasificar los datos de entrenamiento y en teoría , este es el objetivo fundamental del entrenamiento:seguir modificando pesos hasta alcanzar el mínimo global.

Sin embargo, sabemos que las redes neuronales son capaces de aproximar relaciones de entrada-salida extremadamente complejas. El tazón de error anterior no encaja exactamente en la categoría "extremadamente complejo". Es simplemente una gráfica de la función \ (f (x, y) =x ^ 2 + y ^ 2 \).

Pero ahora imagina que la función de error se parece a esto:

O esto:

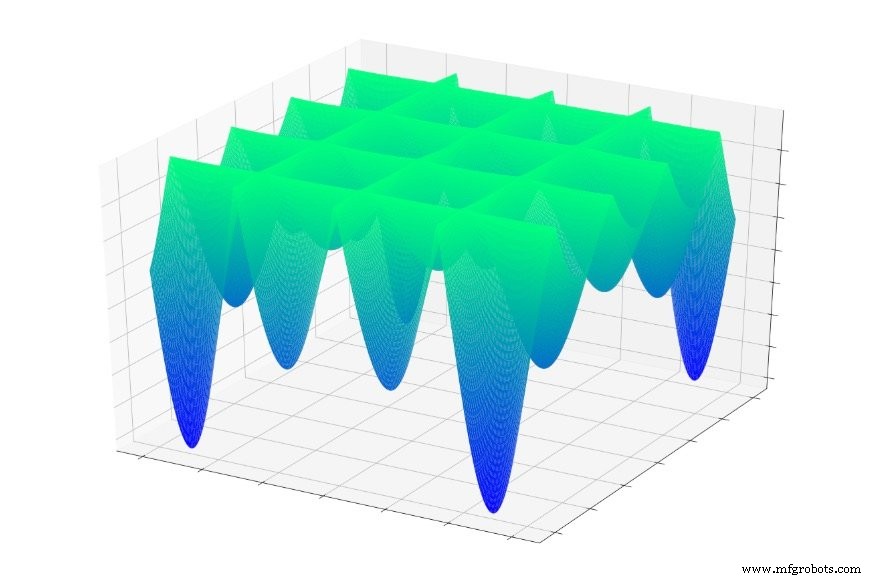
O esto:

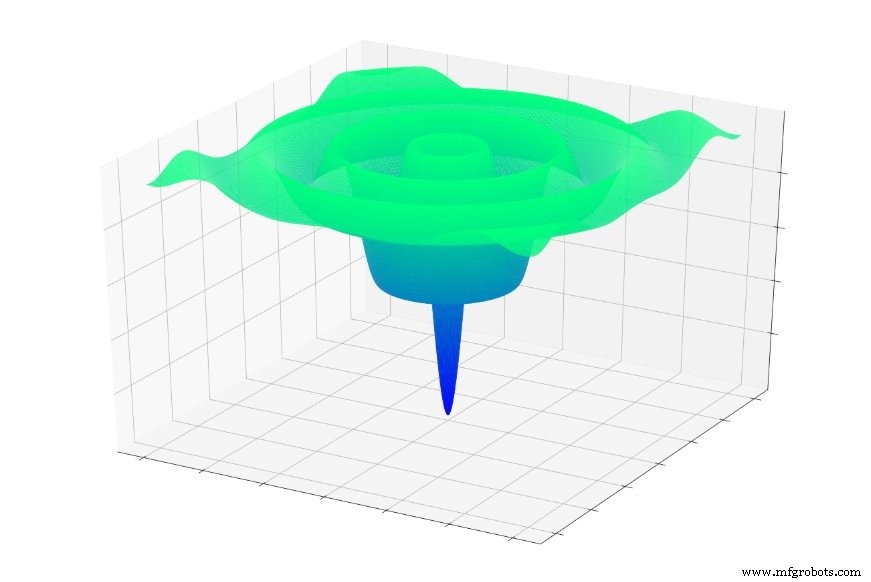
Si saltó al azar a una de estas funciones, a menudo se deslizaría hacia un mínimo local. Estaría en el punto más bajo de una parte localizada del gráfico, pero es posible que no esté cerca del global mínimo.

Lo mismo le puede pasar a una red neuronal. El descenso de gradientes se basa en local información que, esperamos, guíe una red hacia el global mínimo. La red no tiene conocimiento previo sobre las características de la superficie de error general y, en consecuencia, cuando alcanza un punto que parece el fondo de la superficie de error basado en información local , no puede sacar un mapa topográfico y determinar que necesita volver cuesta arriba para encontrar el punto que en realidad es más bajo que todos los demás.

Cuando implementamos el descenso de gradiente básico, le decimos a la red:"Busque el fondo de una superficie de error y quédese allí". No estamos diciendo:"Encuentra la parte inferior de una superficie de error, anota tus coordenadas y luego sigue subiendo y bajando hasta que encuentres la siguiente. Avísame cuando hayas terminado ".

¿Realmente queremos encontrar el mínimo global?

Es razonable suponer que el mínimo global representa la solución óptima y concluir que los mínimos locales son problemáticos porque el entrenamiento podría "estancarse" en un mínimo local en lugar de continuar hacia el mínimo global.

Creo que esta suposición es válida en muchos casos, pero una investigación bastante reciente sobre superficies de pérdida de redes neuronales sugiere que las redes de alta complejidad en realidad pueden beneficiarse de los mínimos locales, porque una red que encuentra el mínimo global estará sobreentrenada y, por lo tanto, será menos efectivo al procesar nuevas muestras de entrada.

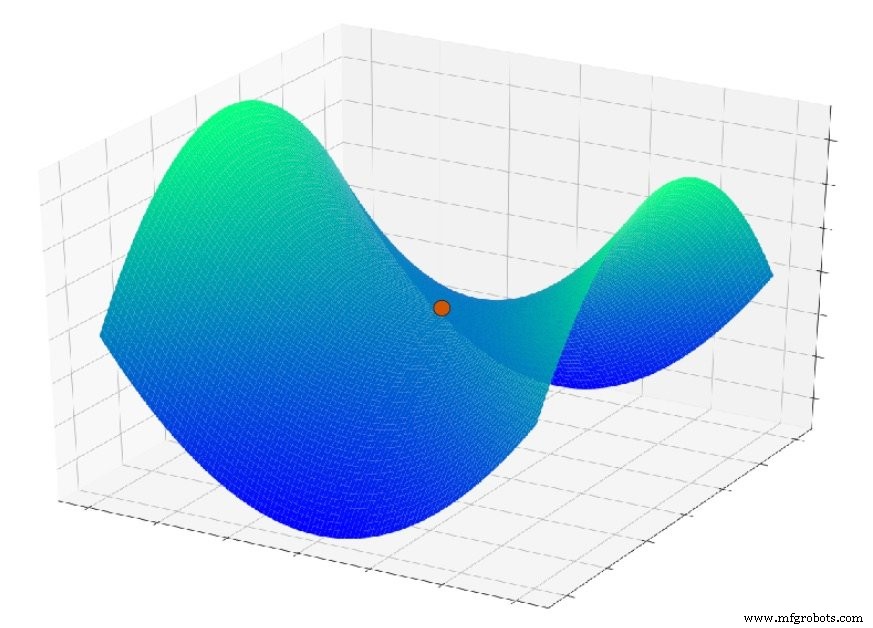
Otro problema que entra en juego aquí es una característica de superficie llamada punto de silla; puede ver un ejemplo en el gráfico a continuación. Es posible que en el contexto de aplicaciones reales de redes neuronales, los puntos de silla en la superficie de error sean de hecho una preocupación más seria que los mínimos locales.

Conclusión

Espero que haya disfrutado de esta discusión sobre mínimos locales. En el próximo artículo, analizaremos algunas técnicas que ayudan a una red neuronal a alcanzar el mínimo global (si es que eso es lo que queremos que haga).