Cómo crear un codificador automático variable con TensorFlow

Aprenda las partes clave de un codificador automático, cómo mejora un codificador automático variacional y cómo crear y entrenar un codificador automático variacional con TensorFlow.

A lo largo de los años, hemos visto muchos campos e industrias aprovechar el poder de la inteligencia artificial (IA) para ampliar los límites de la investigación. La compresión y reconstrucción de datos no es una excepción, donde la aplicación de inteligencia artificial se puede utilizar para construir sistemas más robustos.

En este artículo, veremos un caso de uso muy popular de IA para comprimir datos y reconstruir los datos comprimidos con un codificador automático.

Aplicaciones del codificador automático

Los codificadores automáticos han llamado la atención de muchas personas en el aprendizaje automático, un hecho que se hizo evidente a través de la mejora de los codificadores automáticos y la invención de varias variantes. Han producido algunos resultados prometedores (si no de vanguardia) en varios campos, como la traducción automática neuronal, el descubrimiento de fármacos, la eliminación de ruido de imágenes y varios otros.

Partes del codificador automático

Los autocodificadores, como la mayoría de las redes neuronales, aprenden propagando gradientes hacia atrás para optimizar un conjunto de pesos, pero la diferencia más notable entre la arquitectura de los autocodificadores y la de la mayoría de las redes neuronales es un cuello de botella. Este cuello de botella es un medio de comprimir nuestros datos en una representación de dimensiones inferiores. Otras dos partes importantes de un codificador automático son el codificador y el decodificador.

La fusión de estos tres componentes forma un codificador automático "básico", aunque los más sofisticados pueden tener algunos componentes adicionales.

Echemos un vistazo a estos componentes de forma independiente.

Codificador

Esta es la primera etapa de compresión y reconstrucción de datos y en realidad se ocupa de la etapa de compresión de datos. El codificador es una red neuronal de avance que toma características de datos (como píxeles en el caso de la compresión de imágenes) y genera un vector latente con un tamaño que es menor que el tamaño de las características de datos.

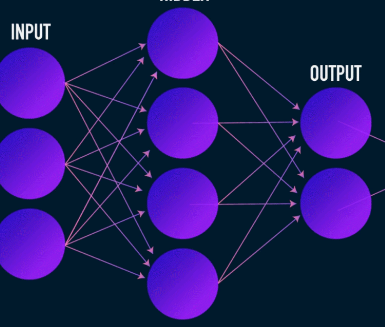
Imagen utilizada por cortesía de James Loy

Para que la reconstrucción de los datos sea robusta, el codificador optimiza sus pesos durante el entrenamiento para exprimir las características más importantes de la representación de los datos de entrada en el vector latente de pequeño tamaño. Esto asegura que el decodificador tenga suficiente información sobre los datos de entrada para reconstruir los datos con una pérdida mínima.

Vector latente (cuello de botella)

El cuello de botella o el componente vectorial latente del autocodificador es la parte más crucial, y se vuelve más crucial cuando necesitamos seleccionar su tamaño.

La salida del codificador es lo que nos da el vector latente y se supone que contiene las representaciones de características más importantes de nuestros datos de entrada. También sirve como entrada a la parte del decodificador y propaga la representación útil al decodificador para su reconstrucción.

Elegir un tamaño más pequeño para el vector latente significa que obtenemos una representación de las características de los datos de entrada con menos información sobre los datos de entrada. La elección de un tamaño de vector latente mucho más grande minimiza la idea de la compresión con codificadores automáticos y también aumenta el costo computacional.

Decodificador

Esta etapa concluye nuestro proceso de reconstrucción y compresión de datos. Al igual que el codificador, este componente también es una red neuronal de retroalimentación, pero se ve un poco diferente estructuralmente del codificador. Esta diferencia proviene del hecho de que el decodificador toma como entrada un vector latente de menor tamaño que el de la salida del decodificador.

La función del decodificador es generar una salida del vector latente que está muy cerca de la entrada.

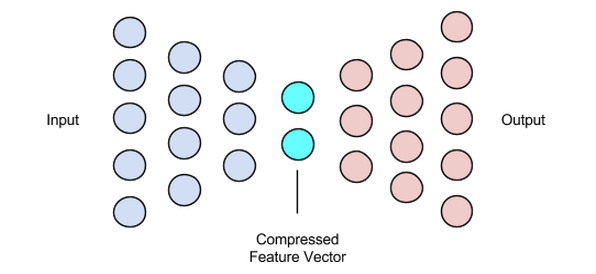
Imagen utilizada por cortesía de Chiman Kwan

Entrenamiento de codificadores automáticos

Por lo general, al entrenar codificadores automáticos, construimos estos componentes juntos en lugar de hacerlo de forma independiente. Los entrenamos de extremo a extremo con un algoritmo de optimización como el descenso de gradientes o el optimizador de ADAM.

Funciones de pérdida

Una parte del procedimiento de entrenamiento del codificador automático que vale la pena discutir es la función de pérdida. La reconstrucción de datos es una tarea de generación y, a diferencia de otras tareas de aprendizaje automático en las que nuestro objetivo es maximizar la probabilidad de predecir la clase correcta, impulsamos nuestra red para producir una salida cercana a la entrada.

Podemos lograr este objetivo con varias funciones de pérdida como l1, l2, error cuadrático medio y un par de otras. Lo que estas funciones de pérdida tienen en común es que miden la diferencia (es decir, qué tan lejos o idéntica) entre la entrada y la salida, por lo que cualquiera de ellas es una opción adecuada.

Redes de codificador automático

Durante todo este tiempo, hemos estado usando un perceptrón multicapa para diseñar nuestro codificador y descodificador, pero resulta que podemos usar marcos más especializados, como redes neuronales convolucionales (CNN) para capturar más información espacial sobre nuestros datos de entrada en el caso de la compresión de datos de imágenes.

Sorprendentemente, la investigación ha demostrado que las redes recurrentes utilizadas como autocodificadores para datos de texto funcionan muy bien, pero no vamos a entrar en eso en el alcance de este artículo. El concepto de un decodificador de vector latente de codificador utilizado en el perceptrón multicapa todavía es válido para los codificadores automáticos convolucionales. La única diferencia es que diseñamos el decodificador y el codificador con capas convolucionales.

Todas estas redes de codificadores automáticos funcionarían bastante bien para la tarea de compresión, pero hay un problema.

Las redes de las que hemos hablado no tienen creatividad. Lo que quiero decir con creatividad cero es que solo pueden generar resultados que hayan visto o con los que hayan sido entrenados.

Podemos inducir cierto nivel de creatividad modificando un poco el diseño de nuestra arquitectura. El resultado se conoce como codificador automático variacional.

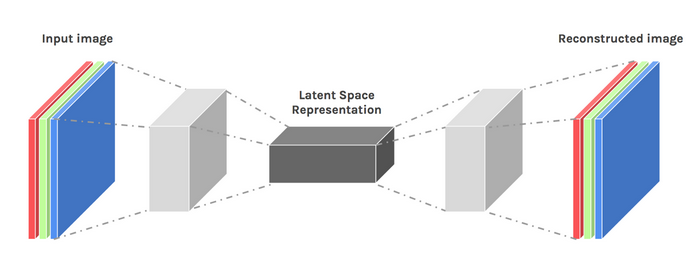
Imagen utilizada por cortesía de Dawid Kopczyk

Autocodificador variacional

El codificador automático variacional introduce dos cambios de diseño importantes:

• En lugar de traducir la entrada a una codificación latente, generamos dos vectores de parámetros:media y varianza.
• Un término de pérdida adicional llamado pérdida por divergencia KL se agrega a la función de pérdida inicial.

La idea detrás del autocodificador variacional es que queremos que nuestro decodificador reconstruya nuestros datos utilizando vectores latentes muestreados a partir de distribuciones parametrizadas por un vector medio y un vector de varianza generado por el codificador.

Las características de muestreo de una distribución otorgan al decodificador un espacio controlado desde el que generar. Después de entrenar un autocodificador variacional, siempre que realizamos un pase directo con datos de entrada, el codificador genera un vector de media y varianza responsable de determinar la distribución a partir de la cual muestrear el vector latente.

El vector medio determina dónde debe centrarse la codificación de los datos de entrada y la varianza determina el espacio radial o el círculo donde queremos elegir la codificación para generar una salida realista. Esto significa que, con cada pasada hacia adelante con los mismos datos de entrada, nuestro codificador automático variacional puede generar diferentes variantes de la salida centradas alrededor del vector medio y dentro del espacio de varianza.

A modo de comparación, cuando miramos un codificador automático estándar, cuando intentamos generar una salida en la que la red no ha sido entrenada, genera salidas poco realistas debido a la discontinuidad en el espacio vectorial latente que produce el codificador.

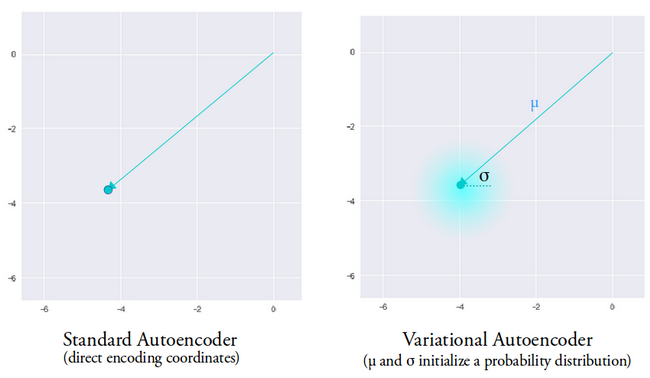
Imagen utilizada por cortesía de Irhum Shafkat

Ahora que tenemos una comprensión intuitiva de un codificador automático variacional, veamos cómo crear uno en TensorFlow.

Código de TensorFlow para un codificador automático variable

Comenzaremos nuestro ejemplo preparando nuestro conjunto de datos. En aras de la simplicidad, usaremos el conjunto de datos MNIST.

(train_images, _), (test_images, _) =tf.keras.datasets.mnist.load_data ()

train_images =train_images.reshape (train_images.shape [0], 28, 28, 1) .astype ('float32')

test_images =test_images.reshape (test_images.shape [0], 28, 28, 1) .astype ('float32')

# Normalizando las imágenes al rango de [0., 1.]

train_images / =255.

test_images / =255.

# Binarización

train_images [train_images> =.5] =1.

train_images [train_images <.5] =0.

test_images [test_images> =.5] =1.

test_images [test_images <.5] =0.

TRAIN_BUF =60000

BATCH_SIZE =100

TEST_BUF =10000

train_dataset =tf.data.Dataset.from_tensor_slices (train_images) .shuffle (TRAIN_BUF) .batch (BATCH_SIZE)

test_dataset =tf.data.Dataset.from_tensor_slices (test_images) .shuffle (TEST_BUF) .batch (BATCH_SIZE)

Obtenga el conjunto de datos y prepárelo para la tarea.

clase CVAE (tf.keras.Model):

def __init __ (self, latent_dim):

super (CVAE, self) .__ init __ ()

self.latent_dim =latent_dim

self.inference_net =tf.keras.Sequential (

[

tf.keras.layers.InputLayer (input_shape =(28, 28, 1)),

tf.keras.layers.Conv2D (

filtros =32, kernel_size =3, strides =(2, 2), activación ='relu'),

tf.keras.layers.Conv2D (

filtros =64, kernel_size =3, strides =(2, 2), activación ='relu'),

tf.keras.layers.Flatten (),

# Sin activación

tf.keras.layers.Dense (latent_dim + latent_dim),

]

)

self.generative_net =tf.keras.Sequential (

[

tf.keras.layers.InputLayer (input_shape =(latent_dim,)),

tf.keras.layers.Dense (unidades =7 * 7 * 32, activación =tf.nn.relu),

tf.keras.layers.Reshape (target_shape =(7, 7, 32)),

tf.keras.layers.Conv2DTranspose (

filtros =64,

kernel_size =3,

strides =(2, 2),

padding ="MISMO",

activación ='relu'),

tf.keras.layers.Conv2DTranspose (

filtros =32,

kernel_size =3,

strides =(2, 2),

padding ="MISMO",

activación ='relu'),

# Sin activación

tf.keras.layers.Conv2DTranspose (

filtros =1, kernel_size =3, strides =(1, 1), padding ="SAME"),

]

)

@ tf.function

def sample (self, eps =None):

si eps es Ninguno:

eps =tf.random.normal (forma =(100, self.latent_dim))

return self.decode (eps, apply_sigmoid =True)

def encode (self, x):

mean, logvar =tf.split (self.inference_net (x), num_or_size_splits =2, axis =1)

return mean, logvar

def reparametrizar (self, mean, logvar):

eps =tf.random.normal (shape =mean.shape)

return eps * tf.exp (logvar * .5) + mean

def decode (self, z, apply_sigmoid =False):

logits =self.generative_net (z)

si apply_sigmoid:

probs =tf.sigmoid (logits)

devolver problemas

return logits

Los dos fragmentos de código preparan nuestro conjunto de datos y construyen nuestro modelo de codificador automático variacional. En el fragmento de código del modelo, hay un par de funciones auxiliares para realizar la codificación, el muestreo y la decodificación.

Reparametrización para calcular gradientes

Existe una función de reparametrización que no hemos discutido, pero que resuelve un problema muy crucial en nuestra red de codificadores automáticos variacionales. Recuerde que durante la etapa de decodificación, tomamos muestras del vector latente que codifica a partir de una distribución controlada por el vector de media y varianza generado por el codificador. Esto no genera ningún problema cuando se reenvían los datos a través de nuestra red, pero causa un gran problema cuando se retropropagan los gradientes del decodificador al codificador, ya que la operación de muestreo no es diferenciable.

En términos simples, no podemos calcular gradientes a partir de una operación de muestreo.

Una buena solución para este problema es aplicar el truco de reparametrización. Esto funciona generando primero una distribución gaussiana estándar de media 0 y varianza 1 y luego realizando una operación de suma y multiplicación diferenciable en esta distribución con la media y varianza generadas por el codificador.

Observe que transformamos la varianza en espacio logarítmico en el código. Esto es para asegurar la estabilidad numérica. El término de pérdida adicional, la pérdida por divergencia de Kullback-Leibler, se introduce para garantizar que las distribuciones que generamos sean lo más cercanas posible a una distribución gaussiana estándar con media 0 y varianza 1.

Llevar las medias de las distribuciones a cero asegura que las distribuciones que generamos estén muy próximas entre sí para evitar discontinuidades entre distribuciones. Una varianza cercana a 1 significa que tenemos un espacio más moderado (es decir, no muy grande ni muy pequeño) para generar codificaciones.

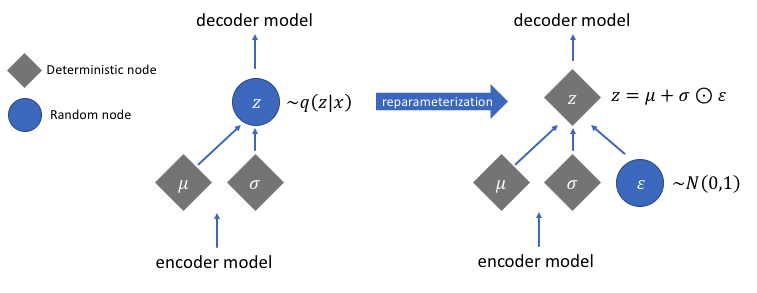
Imagen utilizada por cortesía de Jeremy Jordan

Después de realizar el truco de reparametrización, la distribución obtenida al multiplicar el vector de varianza con una distribución gaussiana estándar y sumar el resultado al vector de media es muy similar a la distribución inmediatamente controlada por los vectores de media y varianza.

Pasos sencillos para crear un codificador automático variable

Terminemos este tutorial resumiendo los pasos para crear un codificador automático variacional:

1. Cree las redes de codificadores y decodificadores.
2. Aplique un truco de reparametrización entre el codificador y el decodificador para permitir la propagación hacia atrás.
3. Entrene ambas redes de un extremo a otro.

El código completo utilizado anteriormente se puede encontrar en el sitio web oficial de TensorFlow.

Imagen destacada modificada de Chiman Kwan