Ley de corriente y voltaje de Kirchhoff (KCL y KVL) | Ejemplo resuelto

KCL y KVL:primera y segunda leyes de Kirchhoff con un ejemplo resuelto

Un físico alemán, "Robert Kirchhoff", introdujo dos importantes leyes eléctricas en 1847 mediante las cuales podemos encontrar fácilmente la resistencia equivalente de una red compleja y las corrientes que fluyen en diferentes conductores. Tanto los circuitos de CA como los de CC se pueden resolver y simplificar mediante el uso de estas leyes simples que se conocen como Ley de corriente de Kirchhoff (KCL) y Ley de voltaje de Kirchhoff (KVL).

También tenga en cuenta que KCL se deriva de la ecuación de continuidad de carga en electromagnetismo, mientras que KVL se deriva de la ecuación de Maxwell - Faraday para el campo magnético estático (la derivada de B con respecto al tiempo es 0 ).

Ley de corriente de Kirchhoff (LCK):

Según KCL:

En cualquier red eléctrica, la suma algebraica de las corrientes entrantes a un punto y las corrientes salientes desde ese punto es cero. O las corrientes de entrada a un punto son iguales a las corrientes de salida de ese punto.

En otras palabras, la suma de las corrientes que fluyen hacia un punto es igual a la suma de las que se alejan de él. O la suma algebraica de las corrientes que ingresan a un nodo es igual a la suma algebraica de las corrientes que lo abandonan.

Explicación de KCL:

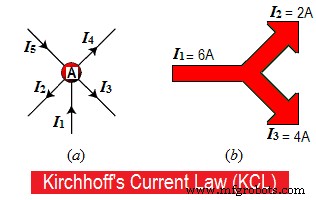
Supongamos que algunos conductores se encuentran en un punto "A" como se muestra en la figura 1.a. En algunos conductores, las corrientes entran al punto "A", mientras que en otros conductores, las corrientes salen o salen del punto "A".

Considere las corrientes entrantes o entrantes como "Positivo (+) hacia el punto "A", mientras que las corrientes salientes o salientes del punto "A" son "Negativas (-)".
entonces:

Yo ₁ + (–yo ₂ ) + (–yo ₃ ) + (–yo ₄ ) + yo ₅ =0

O

Yo ₁ + yo ₅ – Yo ₂ – Yo ₃ – Yo ₄ =0

O

Yo ₁ + yo ₅ =yo ₂ + yo ₃ + yo ₄ =0

es decir,

Corrientes entrantes o entrantes =Corrientes salientes o salientes

O

ΣYo Entrando =ΣI Dejando

Por ejemplo, 8A se acerca a un punto y 5A más 3A salen de ese punto en la figura 1.b, por lo tanto,

8A =5A + 3A

8A =8A.

Ley de voltaje de Kirchhoff (KVL):

La segunda ley de Kirchhoff o KVL establece que;

En otras palabras, en cualquier circuito cerrado (que también se conoce como Malla), la suma algebraica de la FEM aplicada es igual a la suma algebraica de las caídas de voltaje en los elementos . La segunda ley de Kirchhoff también se conoce como ley de voltaje o ley de malla.

ΣIR=ΣE

Explicación de KVL:

En la figura se muestra un circuito cerrado que contiene dos conexiones de baterías E₁ y E₂ . La suma total de E.M.F de las baterías se indica mediante E₁ -E₂ . La dirección imaginaria de la corriente también se muestra en la fig.

E₁ impulsa la corriente en una dirección que se supone que es positiva mientras E₂ interfiere en la dirección de la corriente (es decir, está en la dirección opuesta a la supuesta dirección de la corriente), por lo tanto, se toma como negativa. La caída de tensión en este circuito cerrado depende del producto de tensión y corriente.

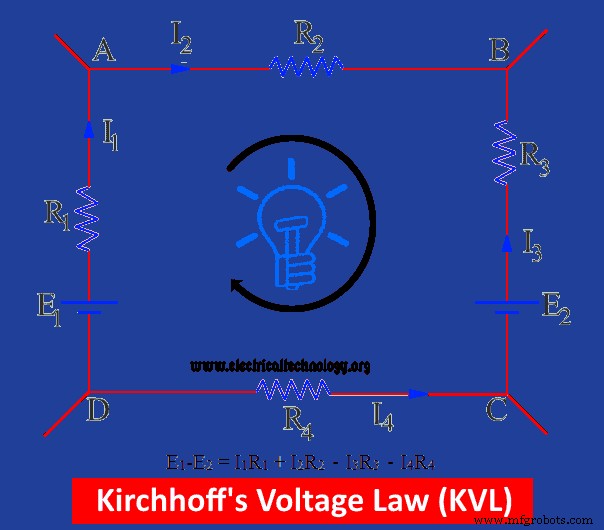
La caída de tensión que se produce en la supuesta dirección de la corriente se conoce como caída de tensión positiva, mientras que la otra es caída de tensión negativa.

En la figura anterior, yo₁ R₁ y yo₂ R₂ son caídas de tensión positivas e I₃ R₃ y yo₄ R₄ son V.D. negativos

Si recorremos el circuito cerrado (o cada malla) y multiplicamos la resistencia del conductor y la corriente que fluye en él, entonces la suma del IR es igual a la suma de las fuentes EMF aplicadas conectadas al circuito.

La ecuación general para el circuito anterior es:

E₁ – E₂ =yo ₁ R₁ + yo ₂ R₂ – yo ₃ R₃ – yo ₄ R₄

Si vamos en la supuesta dirección de la corriente como se muestra en la figura, entonces el producto del IR se toma como positivo, de lo contrario negativo.

Es bueno saberlo:

Dirección de la corriente:

Es muy importante determinar la dirección de la corriente siempre que se resuelvan circuitos a través de las leyes de Kirchhoff. Igual que el caso de corriente de elección y corriente convencional.

La dirección de la corriente se puede asumir en sentido horario o antihorario. Una vez que seleccione la dirección personalizada de la corriente, deberá aplicar y mantener la misma dirección para todo el circuito hasta la solución final del circuito.

Si obtuvimos el valor final como positivo, significa que la supuesta dirección de la corriente era correcta. En caso de valores negativos, la corriente de la dirección se invierte con respecto a la supuesta entonces.

Análisis de circuitos por las leyes de Kirchhoff

Ejemplo resuelto sobre KCL y KVL (Leyes de Kirchhoff)

Ejemplo:

Resistencias de R₁ =10Ω, R₂ =4Ω y R₃ =8Ω se conectan hasta dos baterías (de resistencia despreciable) como se muestra. Encuentre la corriente a través de cada resistencia.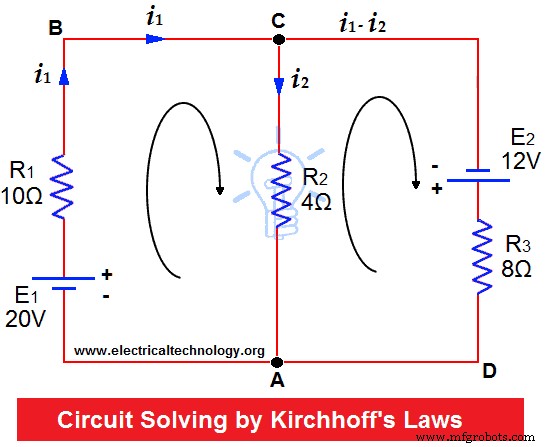

Solución:

Suponga que las corrientes fluyen en las direcciones indicadas por las flechas.

Aplicar KCL en los cruces C y A.

Por lo tanto, actual en la malla ABC =i ₁

Corriente en Malla CA =i ₂

Entonces actual en Mesh CDA =i ₁ – yo ₂

Ahora, aplique KVL en Mesh ABC, 20V actúan en el sentido de las agujas del reloj. Igualando la suma de los productos IR, obtenemos;

10i ₁ + 4yo ₂ =20   …   (1)

En malla ACD, 12 voltios actúan en el sentido de las agujas del reloj, entonces:

8(i ₁ – yo ₂ ) – 4i ₂ =12

8i ₁ – 8yo ₂ – 4yo ₂ =12

8i ₁ – 12yo ₂ =12   …   (2)

Multiplicando la ecuación (1) por 3;

30i ₁ + 12yo ₂ =60

Resolviendo para i ₁

30i ₁ + 12yo ₂ =60

8i ₁ – 12yo ₂ =12

___________
38i ₁ =72

La ecuación anterior también se puede simplificar mediante la Eliminación o la Regla de Cramer.

yo ₁ =72 ÷ 38 =1,895 Amperios =Corriente en resistencia de 10 ohmios

Sustituyendo este valor en (1), obtenemos:

10 (1,895) + 4i ₂ =20

4i ₂ =20 – 18,95

yo ₂ =0,263 amperios =Corriente en resistencias de 4 ohmios.

Ahora,

yo ₁ – yo ₂ =1,895 – 0,263 =1,632 Amperios

Aplicaciones de las Leyes de Kirchhoff

• Las leyes de Kirchhoff se pueden usar para determinar los valores de valores desconocidos como la corriente y el voltaje, así como la dirección de los valores que fluyen de estos quintetos en el circuito.
• Estas leyes se pueden aplicar en cualquier circuito* (Ver la limitación de las Leyes de Kirchhoff al final del artículo), pero son útiles para encontrar los valores desconocidos en redes y circuitos complejos.
• También se utiliza en el análisis de Nodal y Malla para encontrar los valores de corriente y voltaje.
• La corriente a través de cada bucle independiente se transporta aplicando KVL (cada bucle) y la corriente en cualquier elemento de un circuito contando toda la corriente (aplicable en el método de corriente de bucle).
• La corriente a través de cada rama se transporta aplicando KCL (cada unión) KVL en cada bucle de un circuito (aplicable en el método de corriente de bucle).
• Las Leyes de Kirchhoff son útiles para comprender la transferencia de energía a través de un circuito eléctrico.

Es bueno saberlo:

Estas reglas generales deben tenerse en cuenta al simplificar y analizar circuitos eléctricos según las Leyes de Kirchhoff:

• La caída de tensión en un bucle debido a la corriente en el sentido de las agujas del reloj se considera una caída de tensión positiva (+).
• La caída de tensión en un bucle debido a la corriente en dirección contraria a las agujas del reloj se considera una caída de tensión negativa (-).
• La corriente derivada de la batería en el sentido de las agujas del reloj se toma como Positivo (+).
• La corriente derivada de la batería en dirección contraria a las agujas del reloj se toma como positiva (-).

Limitaciones de las leyes de Kirchhoff:

• KCL es aplicable en el supuesto de que la corriente fluye solo en conductores y cables. Mientras que en los circuitos de alta frecuencia, la capacitancia parásita ya no se puede ignorar. En tales casos, la corriente puede fluir en un circuito abierto porque en estos casos, los conductores o cables actúan como líneas de transmisión.
• KVL se aplica suponiendo que no hay un campo magnético fluctuante que une el circuito cerrado. Si bien, en presencia de un campo magnético cambiante en circuitos de CA de alta frecuencia pero de longitud de onda corta, el campo eléctrico no es un campo vectorial conservativo. Entonces, el campo eléctrico no puede ser el gradiente de ningún potencial y la integral de línea del campo eléctrico alrededor del bucle no es cero, lo que contradice directamente a KVL. Es por eso que KVL no es aplicable en tal condición.
• Durante la transferencia de energía del campo magnético al campo eléctrico, donde se debe introducir fudge en KVL para hacer que las P.d (diferencias de potencial) alrededor del circuito sean iguales a 0.

Publicaciones relacionadas sobre teoremas de análisis de circuitos eléctricos:

• Teorema de Thevenin. Procedimiento paso a paso con ejemplo resuelto
• Teorema de Norton. Procedimiento sencillo paso a paso con ejemplo (vistas pictóricas)
• Análisis de circuito SUPERNODO | Paso a paso con ejemplo resuelto
• Análisis de circuito SUPERMESH | Paso a paso con ejemplo resuelto
• Teorema de transferencia de potencia máxima para circuitos de CA y CC
• Teorema de compensación:prueba, explicación y ejemplos resueltos
• Teorema de sustitución:guía paso a paso con ejemplo resuelto
• Teorema de Millman:análisis de circuitos de CA y CC:ejemplos
• Teorema de superposición:análisis de circuito con ejemplo resuelto
• Teorema de Tellegen:ejemplos resueltos y simulación de MATLAB
• Regla del divisor de voltaje (VDR):ejemplos resueltos para circuitos R, L y C
• Regla del divisor de corriente (CDR):ejemplos resueltos para circuitos de CA y CC
• Ley de Ohm:Explicación simple con declaraciones y fórmulas
• Conversión de estrella a delta y delta a estrella. Transformación Y-Δ