Análisis de circuito SUPERMESH | Paso a paso con ejemplo resuelto

Supermesh  Análisis: Declaración , Fórmula, Ejemplos resueltos

¿Qué es el análisis de supermalla?

Análisis de Supermesh o Supermesh es una mejor técnica en lugar de usar Análisis de malla para analizar un circuito o red eléctrica tan compleja, donde dos mallas tienen como elemento común una fuente de corriente. Esto es lo mismo donde usamos Análisis de circuito de supernodo en lugar de Análisis de nodo o circuito nodal para simplificar una red de este tipo donde el supernodo asignado, encerrando completamente la fuente de voltaje dentro del supernodo y reduciendo la cantidad de nodos que no son de referencia en uno (1) para cada fuente de voltaje.

En la técnica de análisis de circuito de supermalla, la fuente de corriente está en el área interior de la supermalla. Por lo tanto, podemos reducir el número de mallas en uno (1) por cada fuente de corriente presente en el circuito.

La malla simple puede ignorarse si la fuente de corriente (en esa malla) se encuentra en el perímetro del circuito. Alternativamente, KVL (Ley de voltaje de Kirchhoff) se aplica solo a esas mallas o supermallas en el circuito renovado.

Por cierto, es difícil de entender por el Preámbulo, por lo que primero resolveremos un circuito simple mediante análisis de circuito de supermalla, y luego, resumiremos todo el análisis de supermalla (paso paso a paso).

• Publicación relacionada:Análisis del circuito SUPERNODO | Paso a Paso con Ejemplo Resuelto

Ejemplo resuelto de análisis de supermalla

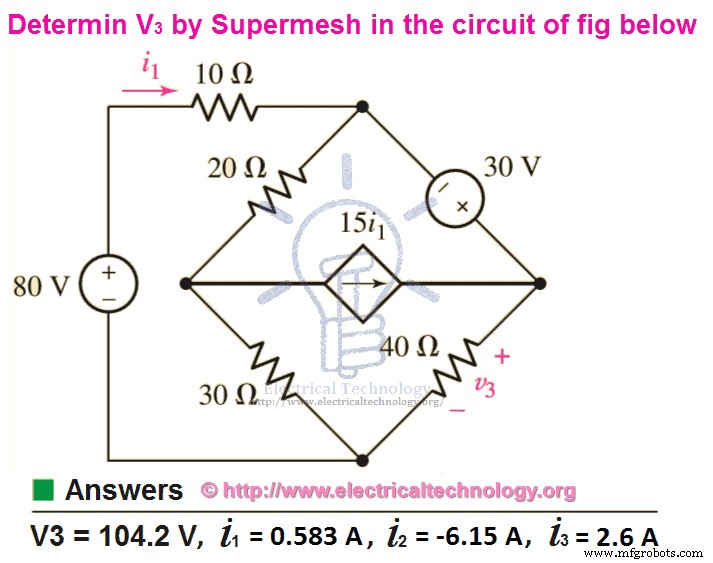
Ejemplo:

Usar análisis de malla para encontrar V₃ y actual i ₁ , yo ₂ y yo ₃ en la siguiente figura?

Solución:

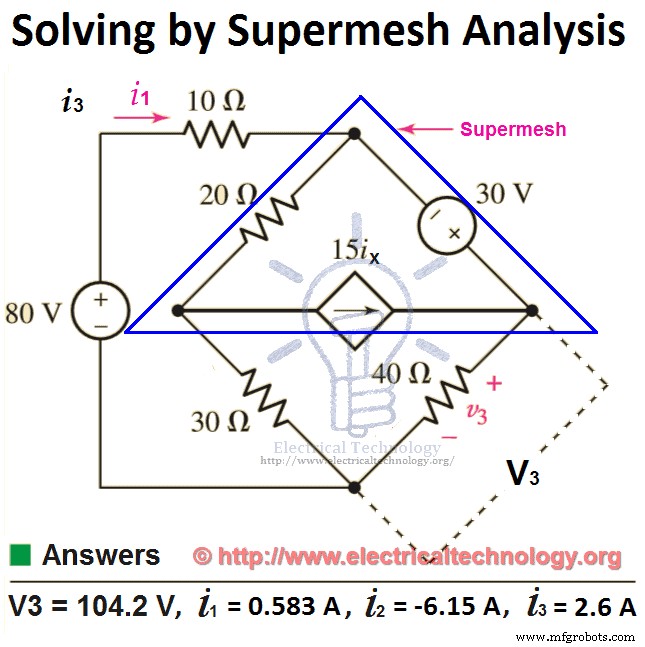
Uso de KVA en malla 1.

80 =10i ₁ + 20(yo ₁ –  yo ₂ ) + 30 (i ₁ – i₃ )

Simplificando

80 =10i ₁ + 20yo ₁ –  20i ₂ + 30yo ₁ – 30i ₃

80 =60i ₁ – 20yo ₂ –  30i ₃ ..... → Ecuación 1.

Ahora aplica KVL en supermalla (que es la integración de mesh 2 y malla 3 , pero lo hemos reducido a una sola malla que se conoce como supermesh )

30 =40i ₃ + 30(i ₃ – yo ₁ ) +20(yo ₂ – yo ₁ )

30 =40i ₃ + 30yo ₃ – 30i ₁ + 20yo ₂ – 20i ₁

30 =70i ₃ – 50yo ₁ + 20yo ₂ …….. → Ecuación 2.

Pero aquí tenemos tres (3) variables, es decir, i 1, yo 2 y yo 3. Y hay dos ecuaciones. Así que también debemos necesitar tres ecuaciones.

La fuente de corriente independiente (en la supermesh ) está relacionado con las corrientes de malla supuestas, es decir,

15i x =yo ₃ – yo ₂

yo ₃ =15yo x + yo ₂ …….. → Ecuación 3.

Resolviendo las ecuaciones 1, 2 y 3 por regla de Cramer o Cramer calculadora de reglas , Eliminación , Eliminación de Gauss o programa asistido por computadora como MATLAB , encontramos

i ₁ =0,583 A

yo ₂ =-6,15 A

i ₃ =2,6 A

Además, podemos encontrar el valor de V₃ ,

V₃ =yo ₃ xR₃

Poniendo los valores,

V₃ =2,6A x 40Ω

V₃ =104 V.

Resumen del análisis de supermalla (paso a paso)

1. Evaluar si el circuito es un circuito plano . en caso afirmativo, aplique Supermesh. Si no, realice un análisis nodal en su lugar.
2. Redibujar el circuito si es necesario y cuente el número de mallas en el circuito.
3. Etiquete cada una de las corrientes de malla en el circuito . Como regla general, definir todas las corrientes de malla para que fluyan en el sentido de las agujas del reloj da como resultado un análisis de circuito más simple.
4. Formar una supermalla si el circuito contiene fuentes de corriente por dos mallas . Entonces, la supermalla encerraría ambas mallas.
5. Escribir un KVL ( de Kirchhoff Ley de voltaje) alrededor de cada malla y supermalla en el circuito . Comience con un nodo fácil y se ajustará. Ahora proceda en la dirección de la corriente de malla. Tome el signo "-" en la cuenta mientras escribe ecuaciones KVL y resuelve el circuito. No se necesita una ecuación KVL si una fuente de corriente se encuentra en la periferia de una malla. Por lo tanto, la corriente de malla se determina y evalúa mediante inspección.
6. Se necesita una KCL (ley de la corriente de Kirchhoff) para cada supermalla definida y se puede lograr con una simple aplicación de la KCL. en palabras simples, relacione la corriente que fluye desde cada fuente de corriente con las corrientes de malla.
7. Se puede producir un caso adicional si el circuito contiene más fuentes dependientes. En este caso, exprese cualquier valor y cantidad desconocidos adicionales, como corrientes o voltajes distintos de las corrientes de malla, en términos de corrientes de malla adecuadas.
8. Ordena y organiza el sistema de ecuaciones.
9. Por fin, resuelva el sistema de ecuaciones para los voltajes nodales como V₁ , V₂ , y V₃ etc. habrá Malla de ellos. si encuentra dificultades para resolver el sistema de ecuaciones, consulte el ejemplo anterior.

Publicaciones relacionadas:

• Teorema de Thevenin. Procedimiento paso a paso con ejemplo resuelto
• Teorema de Norton. Procedimiento sencillo paso a paso con ejemplo (vistas pictóricas)
• Ley de Ohm:explicación simple con declaraciones y fórmulas
• Teorema de transferencia de potencia máxima para circuitos de CA y CC
• Ley de corriente y voltaje de Kirchhoff (KCL y KVL) | Ejemplo resuelto
• Teorema de compensación:prueba, explicación y ejemplos resueltos
• Teorema de sustitución:guía paso a paso con ejemplo resuelto
• Teorema de Millman:análisis de circuitos de CA y CC:ejemplos
• Teorema de superposición:análisis de circuito con ejemplo resuelto
• Teorema de Tellegen:ejemplos resueltos y simulación de MATLAB
• Regla del divisor de voltaje (VDR):ejemplos resueltos para circuitos R, L y C
• Regla del divisor de corriente (CDR):ejemplos resueltos para circuitos de CA y CC
• Conversión de estrella a delta y delta a estrella. Transformación Y-Δ