Calculadora de la regla de Cramer:sistema de 2 y 3 ecuaciones

Calculadora y regla de Cramer para análisis de circuitos lineales | Paso a Paso con Ejemplos Resueltos

Hoy, vamos a compartir otra técnica de análisis de circuitos simple pero poderosa que se conoce como "Regla de Cramer “.

• Análisis de circuitos SUPERMESH | Paso a paso con ejemplo resuelto

Actualización: Hemos agregado la Calculadora de la regla de Cramer en línea donde puede resolver un sistema de dos ecuaciones así como un sistema de tres ecuaciones. Consulte la calculadora de la regla de Cramer en ambas secciones de la publicación. Gracias

A continuación se muestra el tutorial paso a paso de ejemplos resueltos, que explica cómo resolver un circuito y una red eléctricos complejos mediante la regla de Cramer.

Calculadora de la regla de Cramer para 2×2 (Sistema de dos ecuaciones)

Ejemplo 2: Use Análisis de malla para determinar las tres corrientes de malla en el siguiente circuito. Use la regla de Cramer para simplificar.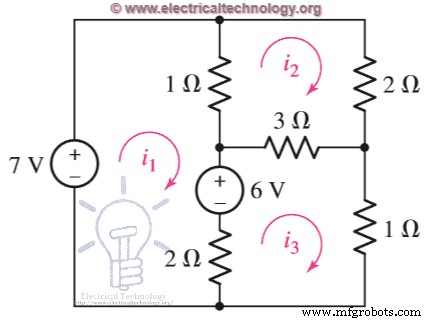 En primer lugar, aplique el KVL en cada malla una por una y escriba sus ecuaciones. -7+1(yo ₁ –yo ₂ ) +6+2(yo ₁ –yo ₃ ) =0         1(i ₂ – yo ₁ ) + 2yo ₂ + 3(yo ₂ – yo ₃ ) =0      2(yo ₃ – yo ₁ ) – 6+3(yo ₃ – yo ₂ ) + 1yo ₃ =0Simplificando,     3i ₁ – yo ₂ – 2yo ₃ =1                    … Eq….. (1)  – i ₁ + 6yo ₂ – 3yo ₃ =0                    … Ecuación….. (2) -2i ₁ – 3yo ₂ + 6yo ₃ =6                    … Eq….. (3) Ahora, escriba las ecuaciones anteriores en forma matricial. 3yo ₁ – yo ₂ – 2yo ₃ =1   –yo ₁ + 6yo ₂ – 3yo ₃ =0-2yo ₁ – 3yo ₂ + 6yo ₃ =6  Ahora, encontraremos el coeficiente determinante de ∆. ¿Cómo haremos eso? Simplemente revise la figura a continuación para obtener una mejor explicación. Haga clic en la imagen para ampliar  Así que el paso completo se muestra a continuación. ∆ =+3 (6 x 6) – (- 3 x –3) – (-1 (- 1 x 6)-(-2 x –3) + (-2 (-1 x –3) – (-2 x 6)∆ =81 -12 -30 =39 Ahora, encuentra el ∆₁ de la misma manera que se explicó anteriormente. Pero, simplemente reemplace la primera columna de la matriz con la "Columna de respuesta". Para más detalles, consulte la figura que se muestra a continuación. 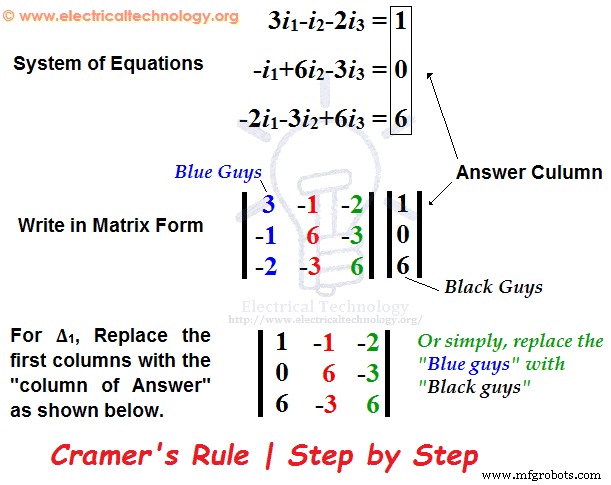Aquí está el paso completo para encontrar ∆₁ . Aquí, reemplazamos los "Blue Guys" en la primera columna con "Black Guys" :). 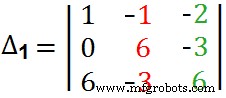=+1(36-9) – (–1[0+18]) –2(0- 36)=27 + 18 + 72∆₁ =117 Nuevamente, encuentra el ∆₂ con el mismo método explicado anteriormente. Simplemente reemplace la segunda columna de la matriz con la "Columna de respuesta", es decir, reemplace los "Chicos rojos" en la columna central con "Chicos negros" como se muestra a continuación. 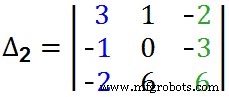=+3 (0 +18) -1[(-6)-(+6)] –2 (-6-0)=54+12+12 =78∆₂ =78 Finalmente, encuentra el último ∆₃ . Simplemente reemplace la tercera columna con la "Columna de respuesta", es decir, reemplace los "Chicos verdes en la tercera columna con" Chicos negros "como se muestra a continuación. =+3 (6 x 6) – (-3 x 0) – [-1(-1 x 6) – (-2 x 0)] + [1(-1) x (-3) – (-2) x (6)]=108 + 6 + 15∆₃ =117 Ahora, resuelve y encuentra los valores desconocidos de la corriente, es decir, i ₁ , yo ₂ y yo ₃ .Como dice la regla de Cramer, las variables, es decir, i ₁ =∆1/∆₁ , yo ₂ =∆/∆₂ y yo ₃ =∆/∆₃ . Por lo tanto, yo ₁ =∆1/∆₁ =117/39yo ₁ =3A Y yo ₂ ,yo ₂ ==∆/∆₂ =78/39yo ₂ =2A Y finalmente, yo ₃ ;yo ₃ =∆/∆₃ =117/39yo ₃ =3A. Espero que hayas entendido muy bien la regla de Cramer y hayas disfrutado del tutorial paso a paso. Por favor, no olvides compartir con tus amigos. Además, ingrese su dirección de correo electrónico en el cuadro a continuación para suscribirse. Entonces, le enviaremos más tutoriales como el anterior. Gracias.

Publicaciones relacionadas y herramientas de análisis de circuitos:

• Teorema de Norton. Procedimiento sencillo paso a paso con ejemplo (vistas pictóricas)
• Teorema de Thevenin. Procedimiento sencillo paso a paso con ejemplo (vistas pictóricas)
• Calculadoras de ingeniería eléctrica y electrónica en línea
• Más de 10 herramientas de diseño y simulación para ingenieros eléctricos/electrónicos en línea
• Diseño de PCB:Cómo diseñar un PCB (paso a paso y vistas pictóricas)
• 15 aplicaciones Android imprescindibles para estudiantes e ingenieros eléctricos y electrónicos
• Análisis del circuito del SUPERNODO | Paso a paso con ejemplo resuelto
• Análisis de circuitos SUPERMESH | Paso a paso con ejemplo resuelto
• Calculadoras de ingeniería eléctrica y electrónica

Análisis de circuito SUPERMESH | Paso a paso con ejemplo resuelto ¿Qué es la caída de voltaje? Calculadora avanzada de caída de tensión con ejemplos resueltos