Sumador completo

El medio sumador es extremadamente útil hasta que desee agregar cantidades de más de un dígito binario. La forma lenta de desarrollar sumadores de dos dígitos binarios sería hacer una tabla de verdad y reducirla. Luego, cuando decida hacer un sumador de tres dígitos binarios, hágalo de nuevo. Luego, cuando decida hacer un sumador de cuatro dígitos, hágalo de nuevo. Entonces, cuando ... Los circuitos serían rápidos, pero el tiempo de desarrollo sería lento.

Observar una suma de dos dígitos binarios muestra lo que necesitamos para extender la suma a varios dígitos binarios.

 11 11 11 --- 110 

Mira cuántas entradas usa la columna del medio. Nuestro sumador necesita tres entradas; a, by el acarreo de la suma anterior, y podemos usar nuestro sumador de dos entradas para construir un sumador de tres entradas.

Σ es la parte fácil. La aritmética normal nos dice que si Σ =a + b + C _in y Σ ₁ =a + b, luego Σ =Σ ₁ + C _en .

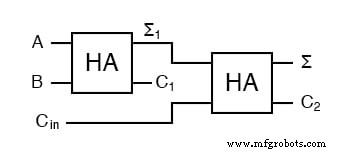
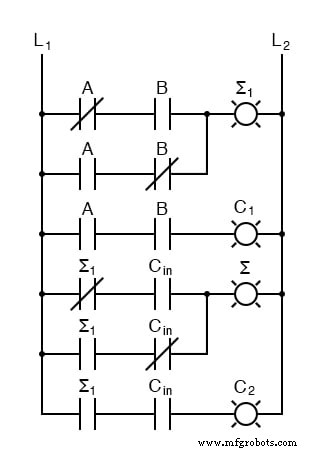
¿Qué hacemos con C ₁ y C ₂ ? Veamos tres sumas de entrada y calculemos rápidamente:

 Cin + a + b =? 0 + 0 + 0 =0 0 + 0 + 1 =1 0 + 1 + 0 =1 0 + 1 + 1 =10 1 + 0 + 0 =1 1 + 0 + 1 =10 1 + 1 + 0 =10 1 + 1 + 1 =11 

Si tiene alguna inquietud sobre el bit de orden inferior, confirme que el circuito y la escalera lo calculan correctamente.

Para calcular el bit de orden superior, observe que es 1 en ambos casos cuando a + b produce un C ₁ . Además, el bit de orden superior es 1 cuando a + b produce a Σ ₁ y C _en es un 1. Así que tendremos un acarreo cuando C ₁ O (Σ ₁ Y C _en ). Nuestro sumador completo de tres entradas es:

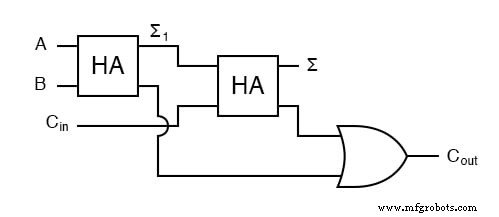
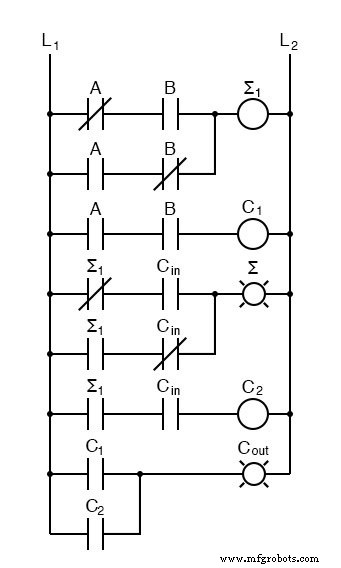
Para algunos diseños, poder eliminar uno o más tipos de puertas puede ser importante, y puede reemplazar la puerta OR final con una puerta XOR sin cambiar los resultados.

Ahora podemos conectar dos sumadores para agregar cantidades de 2 bits.

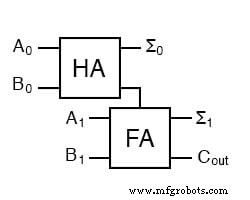
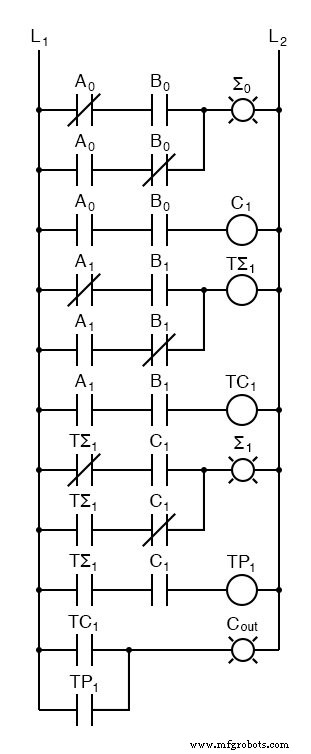
A ₀ es el bit de orden inferior de A, A ₁ es el bit de orden superior de A, B ₀ es el bit de orden inferior de B, B ₁ es el bit de orden superior de B, Σ ₀ es el bit de orden inferior de la suma, Σ ₁ es el bit de orden superior de la suma, y ​​C _out es el Carry.

Un sumador de dos dígitos binarios nunca se haría de esta manera. En cambio, los bits de orden más bajo también pasarían por un sumador completo.

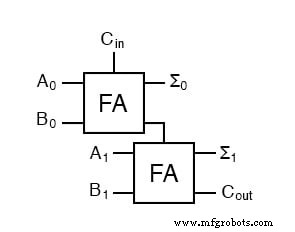
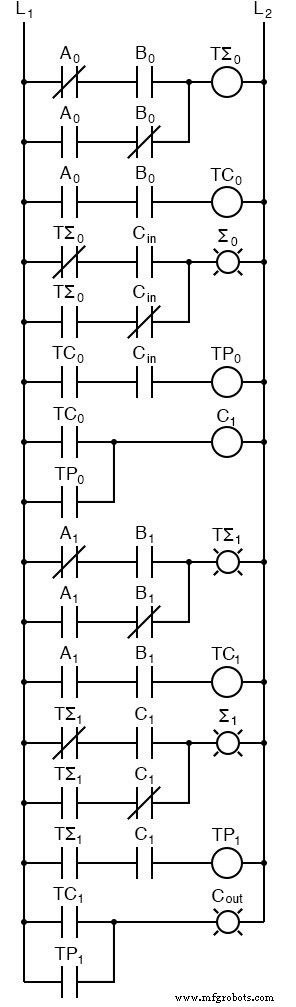
Hay varias razones para esto, una es que luego podemos permitir que un circuito determine si el acarreo de orden más bajo debe incluirse en la suma. Esto permite el encadenamiento de sumas aún mayores. Considere dos formas diferentes de ver una suma de cuatro bits.

 111 1 <- + 11 <+ - 0110 | 01 | 10 1011 | 10 | 11 ----- - | ---- | --- 10001 1 + -100 + -101 

Si permitimos que el programa agregue un número de dos bits y recuerde el acarreo para más adelante, luego usamos ese acarreo en la siguiente suma, el programa puede agregar cualquier número de bits que el usuario desee, aunque solo hayamos proporcionado un sumador de dos bits. Los PLC pequeños también se pueden encadenar juntos para cantidades más grandes.

Estos sumadores completos también se pueden expandir a cualquier número de bits que permita el espacio. Como ejemplo, aquí se explica cómo hacer un sumador de 8 bits.

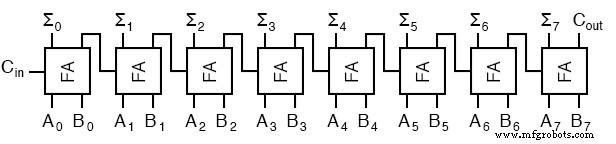
Este es el mismo resultado que usar los dos sumadores de 2 bits para hacer un sumador de 4 bits y luego usar dos sumadores de 4 bits para hacer un sumador de 8 bits o volver a duplicar la lógica de escalera y actualizar los números.

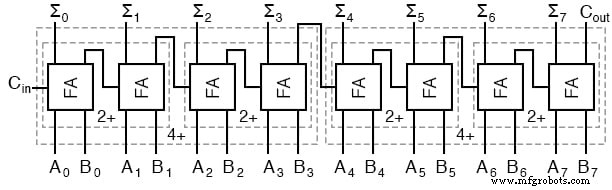
Cada "2+" es un sumador de 2 bits y está compuesto por dos sumadores completos. Cada "4+" es un sumador de 4 bits y está compuesto por dos sumadores de 2 bits. Y el resultado de dos sumadores de 4 bits es el mismo sumador de 8 bits que usamos para construir los sumadores completos.

Para cualquier circuito combinacional grande, generalmente hay dos enfoques de diseño:puede tomar circuitos más simples y replicarlos; o puede diseñar el circuito complejo como un dispositivo completo. El uso de circuitos más simples para construir circuitos complejos le permite dedicar menos tiempo al diseño, pero luego requiere más tiempo para que las señales se propaguen a través de los transistores.

El diseño de sumador de 8 bits anterior tiene que esperar a que todos los C _{x fuera} señales para pasar de A ₀ + B ₀ hasta las entradas de Σ ₇ . Si un diseñador construye un sumador de 8 bits como un dispositivo completo simplificado a una suma de productos, entonces cada señal simplemente viaja a través de una puerta NOT, una puerta AND y una puerta OR.

Un dispositivo de diecisiete entradas tiene una tabla de verdad con 131.072 entradas y reducir 131.072 entradas a una suma de productos llevará algún tiempo. Al diseñar para sistemas que tienen un tiempo de respuesta máximo permitido para proporcionar el resultado final, puede comenzar utilizando circuitos más simples y luego intentar reemplazar partes del circuito que son demasiado lentas.

De esa manera, pasará la mayor parte del tiempo en las partes de un circuito que importan.

HOJA DE TRABAJO RELACIONADA:

• Hoja de trabajo de circuitos matemáticos binarios