home Tecnología de fabricación Equipo de fabricación
Manufactura industrial
Internet industrial de las cosas | Materiales industriales | Mantenimiento y reparación de equipos | Programación industrial |
home  MfgRobots >> Manufactura industrial >  >> Industrial materials >> Nanomateriales

Diseño computacional de material de banda plana

Resumen

La mecánica cuántica establece que el salto integral entre orbitales locales hace que la banda de energía sea dispersiva. Sin embargo, en algunos casos especiales, hay bandas sin dispersión debido a la interferencia cuántica. Estas bandas se denominan banda plana. Se han propuesto muchos modelos que tienen banda plana y se predicen muchas propiedades físicas interesantes. Sin embargo, todavía no se ha encontrado ningún compuesto real que tenga una banda plana a pesar de los 25 años de investigaciones vigorosas. Hemos encontrado que algunos óxidos de pirocloro tienen una banda casi plana justo por debajo del nivel de Fermi según el cálculo de los primeros principios. Además, sus bandas de valencia están bien descritas por un modelo de unión estrecha de celosía de pirocloro con integral de salto de vecino más cercano isotrópico. Este modelo pertenece a una clase de modelo de Mielke, cuyo estado fundamental es ferromagnético con el dopaje de portador apropiado y la interacción repulsiva de Coulomb en el sitio. También hemos realizado un cálculo de banda con polarización de espín para el sistema dopado con agujeros a partir de los primeros principios y hemos descubierto que el estado fundamental es ferromagnético para alguna región de dopaje. Curiosamente, estos compuestos no incluyen elementos magnéticos, como metales de transición y elementos de tierras raras.

Antecedentes

Las propiedades electrónicas y magnéticas de los materiales están determinadas principalmente por su dispersión de energía. Por ejemplo, la conductividad electrónica es alta cuando la banda de valencia / conducción tiene una gran dispersión de energía. Las propiedades magnéticas surgen cuando la dispersión de la banda es pequeña. Por lo general, la dispersión de la banda está determinada por el carácter de la función de onda atómica. Por lo tanto, la mayoría de los compuestos magnéticos contienen elementos magnéticos, como elementos de metales de transición y elementos de tierras raras. Si podemos sintetizar un material magnético que no contenga ningún elemento magnético, su impacto es inconmensurable.

En este artículo, proponemos tal candidato de ferromagnet sin contener elementos magnéticos utilizando el cálculo de los primeros principios. El ancho de banda compuesto por el orbital de un átomo no magnético suele ser pequeño, pero en algunos casos, su ancho de banda se vuelve extremadamente pequeño. Esta banda estrecha se denomina banda plana, y si el nivel de Fermi está justo en esta banda plana, es posible tomar un estado fundamental ferromagnético. Hay muchos estudios de física de banda plana, que se resumen en los artículos de revisión [1, 2].

En este artículo, presentamos brevemente la banda plana. Al principio, consideramos un hamiltoniano de unión estrecha (TB) simple \ ({H} _0 =\ varepsilon \ sum \ limits_i {c} _i ^ {+} {c} _i + \ sum \ limits_ {i, j} {t } _ {ij} {c} _i ^ {+} {c} _j \) (1), donde c i denota el operador de aniquilación en i -sitio, ε es la energía en el sitio y la integral de salto t ij es finito e isotrópico (= t ) solo cuando el sitio i y j estan en el vecino mas cercano. La mecánica cuántica muestra que la integral de salto grande proporciona una gran dispersión de energía en la mayoría de los casos. Por ejemplo, si H 0 se define en una celosía cuadrada simple, la dispersión de energía obtenida es E ( k ) = ε + 2 t (porque k x + Cos k años ). El ancho de banda W =8 t , que es proporcional a t . Desde t está determinada por la superposición de las funciones de onda de tipo atómico, si una banda consta de orbitales s o p, se convierte en una banda ancha. En ese caso, no se espera el estado fundamental magnético porque el estado de espín alineado pierde una gran energía cinética.

Sin embargo, en algunas celosías específicas, esta simple relación W ~ t no se sostiene. Por ejemplo, si H 0 se define en una celosía de pirocloro, aparecen bandas sin dispersión doblemente degeneradas. La celosía de pirocloro se define como la subred del sitio A de la estructura de pirocloro, ver Fig. 1. Podemos demostrar matemáticamente la aparición de esta banda plana, por ejemplo, ver ref [3]. Hay varias celosías que generan bandas planas además de la celosía de pirocloro, por ejemplo, celosía de tablero de ajedrez 2D, celosía de kagome 2D, etc. [1, 2]. Curiosamente, podemos probar que si esta banda plana está medio llena, entonces el sistema tiene el estado fundamental ferromagnético único para cualquier valor positivo de la interacción intraatómica de Coulomb U [4]. Este tipo de celosía que deriva de banda plana se conoce como "celosía geométrica frustrada" en la palabra sistema de espín localizado. De hecho, una serie de óxidos de pirocloro R 2 Ti 2 O 7 (R:elemento de tierras raras) tienen varias propiedades magnéticas novedosas, como líquido de espín cuántico, hielo de espín y monopolo magnético [5,6,7,8,9]. Más recientemente, se encontró una frustración casi perfecta en el imán de dímero frustrado Ba 2 CoSi 2 O 6 Cl 2 [10]. Se ha construido una teoría eficaz de este compuesto, y esta teoría puede explicar las curiosas propiedades magnéticas en el campo magnético alto [11].

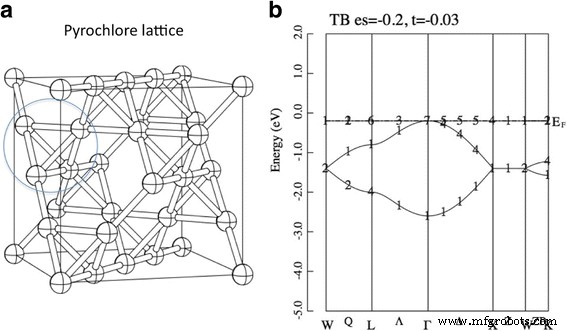
un Celosía de pirocloro. Las bolas y los palos denotan los sitios y enlaces, respectivamente. Esta es la subred del sitio A de A 2 B 2 O 7 estructura de pirocloro. b Dispersión de bandas del modelo de unión estrecha (Ec. 1) en la red de pirocloro. Los parámetros se establecen como ε =- 0.2 y t =- 0.03. La unidad de energía es eV. El número entre ( b ) denota el índice de la representación irreductible, ver ref. [34]

Además del estado fundamental ferromagnético, se sugiere teóricamente que la banda plana induce varias propiedades interesantes, como la superconductividad, el efecto Hall cuántico y varios estados topológicos [12,13,14]. Por lo tanto, es muy importante encontrar un compuesto que realmente tenga una banda plana. Hay varios intentos teóricos de realizar la banda plana utilizando litografía [15] o celosía fotónica [16]. Además de estos materiales mesoscópicos, observamos que una estructura organometálica de indio-fenileno 2D cuidadosamente diseñada (IPOF) muestra una banda plana excelente [17]. Curiosamente, esta banda plana es topológicamente no trivial y puede servir como escenario para el efecto Hall cuántico fraccional de alta temperatura. A pesar de estos vigorosos estudios, el orden magnético de largo alcance esperado aún no se ha logrado, probablemente porque estos intentos son limitados para el sistema 2D. Hay otro estudio interesante que ha mostrado un orden magnético de largo alcance invocado por una molécula orgánica absorbida en el grafeno [18]. Sin embargo, el origen microscópico de este orden magnético aún no está claro.

Como se mencionó anteriormente, para que aparezca el ferromagnetismo usando esta banda plana, es necesario ajustar el nivel de Fermi solo en esta banda plana. En la mayoría de los óxidos de pirocloro A 2 B 2 O 7 , el nivel de Fermi está en la banda compuesta por el orbital del sitio B. Sin embargo, dado que la banda plana tiene que formarse en la subred del sitio A (retícula de pirocloro), el ion del sitio B debe ser inerte. Además, dado que la integral de salto debe ser isotrópica, el nivel de Fermi debe estar en el orbital s del sitio A.

Imponiendo las condiciones anteriores, podemos elegir el candidato de óxidos de pirocloro para tener la banda plana en la parte superior de la banda de valencia:

$$ \ left (\ mathrm {a} \ right) \ {{\ mathrm {A}} ^ {1 +}} _ 2 {{\ mathrm {B}} ^ {6 +}} _ 2 {\ mathrm {O} } _7, \ kern0.75em \ left (\ mathrm {b} \ right) \ {{\ mathrm {A}} ^ {2 +}} _ 2 {{\ mathrm {B}} ^ {5 +}} _ 2 { \ mathrm {O}} _ 7, \ kern1em \ left (\ mathrm {c} \ right) \ {{\ mathrm {A}} ^ {3 +}} _ 2 {{\ mathrm {B}} ^ {4+} } _2 {\ mathrm {O}} _ 7. $$

Dado que la parte superior de la banda de valencia tiene el carácter A-s, el ion del sitio A es típicamente (a) Tl 1+ ; (b) Sn 2+ , Pb 2+ ; y (c) Bi 3+ . Todos estos iones tienen (5s) 2 o (6s) 2 configuración. El sitio B debe ser inerte, por lo que podemos elegir (a) Mo 6+ , W 6+ ; (b) Nb 5+ , Ta 5+ ; y (c) Ti 4+ , Sn 4+ . Todos estos iones del sitio B tienen una capa cerrada, es decir, ( n d) 0 o ( n p) 0 configuración donde n =3, 4, 5.

Entre la combinación anterior, nos centramos en tres compuestos:

$$ \ left (\ mathrm {a} \ right) \ {\ mathrm {Tl}} _ 2 {\ mathrm {Mo}} _ 2 {\ mathrm {O}} _ 7, \ kern0.75em \ left (\ mathrm {b } \ right) \ {\ mathrm {Sn}} _ 2 {\ mathrm {Nb}} _ 2 {\ mathrm {O}} _ 7, \ kern0.75em \ left (\ mathrm {c} \ right) \ {\ mathrm { Bi}} _ 2 {\ mathrm {Ti}} _ 2 {\ mathrm {O}} _ 7. $$

Los compuestos (b) Sn 2 Nb 2 O 7 y (c) Bi 2 Ti 2 O 7 ya se han sintetizado [19,20,21,22,23], mientras que (a) Tl 2 Mo 2 O 7 aún no se ha informado. Sin embargo, un óxido de pirocloro análogo Tl 2 Ru 2 O 7 ya ha sido sintetizado y muestra una transición de metal-aislante única [24]. Dado que el radio atómico de Mo y Ru son similares, esperamos que Tl 2 Mo 2 O 7 se puede sintetizar en determinadas condiciones. Curiosamente, tanto (b) Sn 2 Nb 2 O 7 y (c) Bi 2 Ti 2 O 7 son conocidos por ser candidatos a material fotocatalítico.

Hemos realizado un cálculo de los primeros principios para estos compuestos. Este artículo está organizado de la siguiente manera:En la sección “Métodos” se describe el método de cálculo y las estructuras cristalinas que calculamos. En la sección “Resultados y discusión”, mostramos los resultados calculados y damos un poco de discusión. El resumen se describe en la sección "Conclusiones".

Métodos

Hemos calculado la estructura electrónica de Tl 2 Mo 2 O 7 , Sn 2 Nb 2 O 7 y Bi 2 Ti 2 O 7 desde los primeros principios. Para simplificar, asumimos que todos tienen un A 2 ideal B 2 O 6 Estructura de pirocloro O ′. Dado que hay dos sitios de oxígeno, los llamamos O y O ′ para distinguirlos. Hemos utilizado un esquema de onda plana aumentada de potencial completo (FLAPW) y el potencial de correlación de intercambio se construyó dentro de la aproximación de gradiente general [25]. Utilizamos el programa informático paquete WIEN2k [26]. El parámetro RK máx se elige como 7.0. El k Se toma una malla de puntos de modo que el número total de mallas en la primera zona de Brillouin sea ~ 1000. También hemos optimizado la estructura cristalina, con la fijación de la simetría del grupo espacial. La estructura cristalina de A 2 B 2 O 6 O ′ es el siguiente:Grupo espacial Fd-3m (# 227), A (0,0,0), B (1 / 2,1 / 2,1 / 2), O ( x , 0,0) y O '(1 / 8,1 / 8,1 / 8). Para Sn 2 Nb 2 O 7 y Bi 2 Ti 2 O 7 , utilizamos el parámetro de celosía experimental. Para Tl 2 Mo 2 O 7 , también optimizamos el parámetro de celosía ( a ) y obtuvo a =10.517 Å, que está muy cerca del parámetro de celosía experimental reciente para el compuesto análogo Tl 2 Ru 2 O 7 [27]. En esta estructura, el único parámetro libre es la posición de O (= x ). La convergencia de la posición atómica se juzga por la fuerza que trabaja en cada átomo que es menor que 1.0 mRy / a.u.

Resultados y discusión

Estructura de banda

La Figura 2 muestra la dispersión de la banda de energía de Tl 2 Mo 2 O 7 , Sn 2 Nb 2 O 7 y Bi 2 Ti 2 O 7 desde los primeros principios. Primero, nos enfocamos en el panel del medio, Sn 2 Nb 2 O 7 . La dispersión de la banda obtenida concuerda bien con los estudios anteriores, mientras que no se mencionó la existencia de la banda cuasi-plana [19, 28]. Vemos que la forma de la parte superior de la banda de valencia (- 3 ~ 0 eV) es similar al modelo de unión apretada que se muestra en la Fig. 1b. Este acuerdo es bastante sorprendente porque este modelo solo usa dos parámetros, ε y t . Entonces, como primera aproximación, la banda de valencia de Sn 2 Nb 2 O 7 se describe mediante una banda de TB que consta de los orbitales "Sn-s". Aquí, notamos que estos orbitales "Sn-s" son los orbitales anti-enlace que consisten en orbitales Sn-s y O′-p. La principal diferencia entre las bandas ab-initio y las bandas TB es la planitud de la banda a la energía ~ 0 eV, lo que significa que las integrales de salto distintas de los átomos de Sn vecinos más cercanos también son necesarias para ajustarse con precisión a las bandas ab-initio .

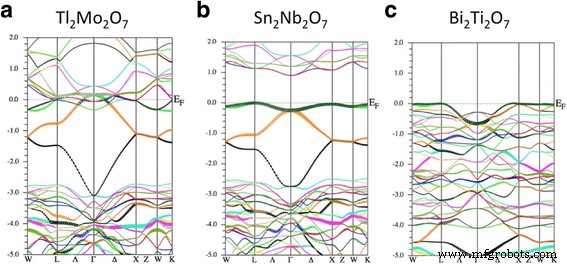
Estructura de banda electrónica de ( a ) Tl 2 Mo 2 O 7 , ( b ) Sn 2 Nb 2 O 7 y ( c ) Bi 2 Ti 2 O 7 . La unidad de energía es eV.

A continuación, discutimos la estructura de bandas de Tl 2 Mo 2 O 7 , que se muestra en el panel izquierdo de la Fig. 2. Podemos ver que la forma de la banda de valencia de Tl 2 Mo 2 O 7 es casi lo mismo que el de Sn 2 Nb 2 O 7 , indicando la existencia de la banda plana en Tl 2 Mo 2 O 7 . Sin embargo, la banda de conducción reduce su energía y la banda prohibida se colapsa. La banda Mo-d está parcialmente ocupada a diferencia del caso de Sn 2 Nb 2 O 7 , lo que indica que la configuración iónica formal Tl 1+ 2 Mes 6+ 2 O 2− 7 no es apropiado. Este resultado sugiere que el análisis por el modelo de carga puntual es bastante efectivo, lo que sugiere que A 1+ 2 B 6+ 2 O 7 no es una configuración estable para óxidos de pirocloro. La banda plana Tl-s está entrelazada con la banda Mo-d, similar al caso de un óxido de pirocloro análogo Tl 2 Ru 2 O 7 [29]. Una transición de metal-aislante se encuentra en Tl 2 Ru 2 O 7 y su causa se atribuye a la banda plana oculta de Tl-s [30]. Podemos esperar que esta transición metal-aislante también se lleve a cabo en Tl 2 Mo 2 O 7 si fue sintetizado.

Finalmente, discutimos la estructura de bandas de Bi 2 Ti 2 O 7 , que se muestra en el panel derecho de la Fig. 2. La dispersión de banda obtenida concuerda bien con el estudio anterior [31]. A pesar de la forma diferente de la banda de valencia entre Bi 2 Ti 2 O 7 y Sn 2 Nb 2 O 7 , la parte superior de la banda de valencia de Bi 2 Ti 2 O 7 es muy plano en la mayor parte del eje de simetría en la zona de Brillouin. Dado que la forma de la banda es diferente a la de la Fig. 1, el origen de esta banda cuasi-plana parcial no puede encontrarse simplemente en la banda plana en la celosía de pirocloro. Sin embargo, la banda cuasi-plana y la alta densidad de estados (DOS) resultante son suficientes para esperar la realización del ferromagnetismo al dopar agujeros. Discutimos este punto en la siguiente subsección.

Estados ferromagnéticos

En la subsección anterior, encontramos una banda casi plana en la parte superior de la banda de valencia en Sn 2 Nb 2 O 7 . Para Bi 2 Ti 2 O 7 , también encontramos una banda casi plana parcial. Dado que son aislantes, tenemos que introducir agujeros en la banda cuasi-plana para inducir el ferromagnetismo. En el caso de la banda plana perfecta, cualquiera valor de la interacción de Coulomb en el sitio U provoca un estado fundamental ferromagnético cuando la banda plana está medio llena [4]. Esto significa que incluso un orbital s o p atómico bien extendido puede causar el estado fundamental ferromagnético. En cuanto al caso de la banda cuasi-plana, un estudio numérico muestra que una cierta U grande> U c puede inducir ferromagnetismo, donde U c es el valor crítico y U c tiene el orden del ancho de banda W [32]. Dado que la estimación de U y U c es difícil en el compuesto real, en su lugar, realizamos un cálculo ab-initio con polarización de espín. Teniendo en cuenta que el cálculo de la banda ha tenido éxito para describir el estado fundamental ferromagnético de bcc Fe, que también tiene una banda estrecha, nuestro enfoque estará justificado. Para simular el dopaje del hoyo, sustituimos N por O ′, es decir, calculamos Sn 2 Nb 2 O 6 N y Bi 2 Ti 2 O 6 N. Dado que esta sustitución reduce dos electrones por celda unitaria primitiva (un electrón por unidad de fórmula), la banda casi plana se llena hasta la mitad.

La Figura 3 muestra la curva de DOS para Sn 2 Nb 2 O 6 N y Bi 2 Ti 2 O 6 N. La banda cuasi plana antes mencionada forma un pico agudo justo alrededor del nivel de Fermi. Podemos ver que ambos compuestos se vuelven semimetálicos, es decir, el estado de espín del electrón con energía E = E F (Energía de Fermi) está completamente polarizada. El momento magnético total M es 2,00 μ B por celda unitaria primitiva para ambos compuestos, lo que también indica que los electrones de conducción están completamente polarizados en espín. El intercambio que se divide entre la banda de giro hacia arriba y hacia abajo es de ~ 0.3 eV para Sn 2 Nb 2 O 6 N y ~ 0,4 eV para Bi 2 Ti 2 O 6 N. Estos valores son mucho más pequeños que la división del intercambio en bcc Fe, ~ 2 eV. Dado que la división de intercambio está determinada aproximadamente por la función de onda atómica [33], la banda d tiene una división de intercambio mayor que la banda s o p. Sin embargo, dado que Sn 2 Nb 2 O 6 N y Bi 2 Ti 2 O 6 N tienen un ancho de banda muy pequeño, la división del intercambio excede el ancho de banda y se da cuenta del estado de tierra semimetálico.

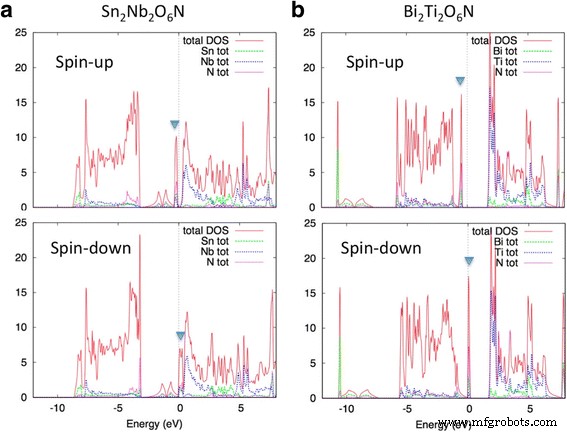
Curva DOS de ( a ) Sn 2 Nb 2 O 6 N y ( b ) Bi 2 Ti 2 O 6 N para estado de espín polarizado. El triángulo relleno muestra la posición de la banda casi plana

Conclusiones

En este artículo, mostramos un principio rector para diseñar compuestos de banda plana. De acuerdo con este principio, elegimos tres óxidos de pirocloro e investigamos su estructura electrónica mediante el estudio de los primeros principios. Combinado con un análisis de unión estrecha, encontramos que algunos compuestos en realidad tienen una banda casi plana. También encontramos que el dopaje de huecos hacia estos compuestos conduce al estado fundamental ferromagnético, a pesar de que estos compuestos no contienen elementos magnéticos. Estos hallazgos serán un gran paso para realizar no solo un sistema de banda plana en un compuesto, sino también un ferromagnético sin incluir un elemento magnético.

Abreviaturas

DOS:

Densidad de estados

FLAPW:

Onda plana aumentada de potencial completo

TB:

Apretado


Nanomateriales

  • Metal
  • Resina
  • fibra
  • Material compuesto
  • Nanomateriales
  • Materiales poliméricos
  • Biologicos
  • Teñir
  • Especias

    1. ¿Qué es la fotopolimerización en la impresión 3D?
    2. ¿Qué es una "carretera" en la impresión 3D?
    3. Los desafíos del diseño de productos
    4. Cambiar diseño de contacto
    5. Diseño a prueba de fallas
    6. Tutorial de Verilog
    7. ¿Qué es el diseño arquitectónico?
    8. La influencia del tipo de material en el diseño del troquel
    9. ¿Qué es el manejo de materiales?
    10. Consideraciones de diseño del transportador de manejo de materiales a granel
    11. Consideraciones para un diseño óptimo de tolva de transferencia de transportador