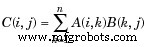MATLAB - Operadores
Un operador es un símbolo que le dice al compilador que realice manipulaciones matemáticas o lógicas específicas. MATLAB está diseñado para operar principalmente en matrices y arreglos completos. Por lo tanto, los operadores de MATLAB funcionan tanto con datos escalares como no escalares. MATLAB permite los siguientes tipos de operaciones elementales −
- Operadores aritméticos
- Operadores relacionales
- Operadores lógicos
- Operaciones bit a bit
- Establecer operaciones
Operadores aritméticos
MATLAB permite dos tipos diferentes de operaciones aritméticas −
- Operaciones aritméticas de matrices
- Operaciones aritméticas de matrices
Las operaciones aritméticas de matrices son las mismas que se definen en el álgebra lineal. Las operaciones con arreglos se ejecutan elemento por elemento, tanto en arreglos unidimensionales como multidimensionales.
Los operadores de matriz y los operadores de matriz se diferencian por el símbolo de punto (.). Sin embargo, como la operación de suma y resta es la misma para matrices y arreglos, el operador es el mismo para ambos casos. La siguiente tabla da una breve descripción de los operadores −
Mostrar ejemplos
| Sr.No. | Operador y descripción |
|---|---|
| 1 | + Suma o plus unario. A+B suma los valores almacenados en las variables A y B. A y B deben tener el mismo tamaño, a menos que uno sea un escalar. Se puede agregar un escalar a una matriz de cualquier tamaño. |
| 2 | - Resta o menos unario. A-B resta el valor de B de A. A y B deben tener el mismo tamaño, a menos que uno sea un escalar. Un escalar se puede restar de una matriz de cualquier tamaño. |
| 3 | * Multiplicación de matrices. C =A*B es el producto algebraico lineal de las matrices A y B. Más precisamente,
Para A y B no escalares, el número de columnas de A debe ser igual al número de filas de B. Un escalar puede multiplicar una matriz de cualquier tamaño. |
| 4 | .* Multiplicación de matrices. A.*B es el producto elemento por elemento de los arreglos A y B. A y B deben tener el mismo tamaño, a menos que uno de ellos sea un escalar. |
| 5 | / División a la derecha de matriz o barra oblicua. B/A es más o menos lo mismo que B*inv(A). Más precisamente, B/A =(A'\B')'. |
| 6 | ./ División derecha de matriz. A./B es la matriz con elementos A(i,j)/B(i,j). A y B deben tener el mismo tamaño, a menos que uno de ellos sea un escalar. |
| 7 | \ Barra invertida o división izquierda de matriz. Si A es una matriz cuadrada, A\B es aproximadamente lo mismo que inv(A)*B, excepto que se calcula de manera diferente. Si A es una matriz n por n y B es un vector columna con n componentes, o una matriz con varias columnas, entonces X =A\B es la solución a la ecuación AX =B . Se muestra un mensaje de advertencia si A está mal escalado o es casi singular. |
| 8 | .\ División izquierda de la matriz. A.\B es la matriz con elementos B(i,j)/A(i,j). A y B deben tener el mismo tamaño, a menos que uno de ellos sea un escalar. |
| 9 | ^ Poder de la matriz. X^p es X elevado a p, si p es un escalar. Si p es un número entero, la potencia se calcula elevando al cuadrado repetidamente. Si el entero es negativo, X se invierte primero. Para otros valores de p, el cálculo implica valores propios y vectores propios, de modo que si [V,D] =eig(X), entonces X^p =V*D.^p/V. |
| 10 | .^ Potencia de matriz. A.^B es la matriz con elementos A(i,j) elevados a B(i,j). A y B deben tener el mismo tamaño, a menos que uno de ellos sea un escalar. |
| 11 | ' Transpuesta de matriz. A' es la transpuesta algebraica lineal de A. Para matrices complejas, esta es la transpuesta conjugada compleja. |
| 12 | .' Transposición de matriz. A.' es la matriz transpuesta de A. Para matrices complejas, esto no implica conjugación. |
Operadores relacionales
Los operadores relacionales también pueden trabajar con datos escalares y no escalares. Los operadores relacionales para arreglos realizan comparaciones elemento por elemento entre dos arreglos y devuelven un arreglo lógico del mismo tamaño, con elementos establecidos en 1 lógico (verdadero) donde la relación es verdadera y elementos establecidos en 0 lógico (falso) donde es no.
La siguiente tabla muestra los operadores relacionales disponibles en MATLAB −
Mostrar ejemplos
| Sr.No. | Operador y descripción |
|---|---|
| 1 | < Menos que |
| 2 | <= Menor o igual que |
| 3 | > Mayor que |
| 4 | >= Mayor o igual que |
| 5 | == Igual a |
| 6 | ~= No es igual a |
Operadores lógicos
MATLAB ofrece dos tipos de operadores lógicos y funciones −
-
Por elementos:estos operadores operan en los elementos correspondientes de matrices lógicas.
-
Cortocircuito:estos operadores operan en expresiones escalares y lógicas.
Los operadores lógicos por elementos operan elemento por elemento en arreglos lógicos. Los símbolos &, | y ~ son los operadores de matrices lógicas AND, OR y NOT.
Los operadores lógicos de cortocircuito permiten el cortocircuito en operaciones lógicas. Los símbolos &&y || son los operadores lógicos de cortocircuito AND y OR.
Mostrar ejemplos
Operaciones bit a bit
Los operadores bit a bit trabajan en bits y realizan operaciones bit a bit. Las tablas de verdad para &, | y ^ son las siguientes −
| p | q | p &q | p | q | p ^ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Suponga que A =60; y B =13; Ahora en formato binario quedarán de la siguiente manera −
A =0011 1100
B =0000 1101
-----------------
A&B =0000 1100
A|B =0011 1101
A^B =0011 0001
~A =1100 0011
MATLAB proporciona varias funciones para operaciones bit a bit como operaciones 'bit a bit y', 'bit a bit o' y 'bit a bit no', operación de desplazamiento, etc.
La siguiente tabla muestra las operaciones bit a bit comúnmente utilizadas −
Mostrar ejemplos
| Función | Propósito |
|---|---|
| bitand(a, b) | Y bit a bit de enteros a y b |
| bitcmp(a) | Complemento bit a bit de a |
| bitget(a,pos) | Obtener bit en la posición especificada pos , en la matriz de enteros a |
| bitor(a, b) | OR bit a bit de enteros a y b |
| conjunto de bits(a, pos) | Establecer bit en una ubicación específica pos de a |
| desplazamiento de bits(a, k) | Devuelve a desplazado a la izquierda por k bits, equivalente a multiplicar por 2 k . Los valores negativos de k corresponden a desplazar bits a la derecha o dividir por 2 |k| y redondeando al entero más cercano hacia infinito negativo. Los bits de desbordamiento se truncan. |
| bitxor(a, b) | XOR bit a bit de enteros a y b |
| intercambiar bytes | Intercambiar orden de bytes |
Establecer operaciones
MATLAB proporciona varias funciones para operaciones de conjuntos, como unión, intersección y prueba de pertenencia a conjuntos, etc.
La siguiente tabla muestra algunas operaciones de conjuntos de uso común −
Mostrar ejemplos
| Sr.No. | Función y descripción |
|---|---|
| 1 | intersección(A,B) Establecer intersección de dos matrices; devuelve los valores comunes a A y B. Los valores devueltos están ordenados. |
| 2 | intersecar(A,B,'filas') Trata cada fila de A y cada fila de B como entidades únicas y devuelve las filas comunes a A y B. Las filas de la matriz devuelta están ordenadas. |
| 3 | esmiembro(A,B) Devuelve una matriz del mismo tamaño que A, que contiene 1 (verdadero) donde los elementos de A se encuentran en B. En cualquier otro lugar, devuelve 0 (falso). |
| 4 | esmiembro(A,B,'filas') Trata cada fila de A y cada fila de B como entidades únicas y devuelve un vector que contiene 1 (verdadero) donde las filas de la matriz A también son filas de B. En otros lugares, devuelve 0 (falso). |
| 5 | clasificado(A) Devuelve 1 lógico (verdadero) si los elementos de A están ordenados y 0 lógico (falso) en caso contrario. La entrada A puede ser un vector o una matriz de cadenas de celdas N-por-1 o 1-por-N. Se considera que A está ordenado si A y la salida de sort(A) son iguales. |
| 6 | ordenado(A, 'filas') Devuelve 1 lógico (verdadero) si las filas de la matriz bidimensional A están ordenadas y 0 lógico (falso) en caso contrario. La matriz A se considera ordenada si A y la salida de sortrows(A) son iguales. |
| 7 | fijardiferencia(A,B) Establece la diferencia de dos matrices; devuelve los valores de A que no están en B. Los valores de la matriz devuelta están ordenados. |
| 8 | setdiff(A,B,'filas') Trata cada fila de A y cada fila de B como entidades únicas y devuelve las filas de A que no están en B. Las filas de la matriz devuelta están ordenadas. La opción 'filas' no admite matrices de celdas. |
| 9 | setxor Establece OR exclusivo de dos matrices |
| 10 | sindicato Establece la unión de dos arreglos |
| 11 | único Valores únicos en matriz |
MATLAB