Filtros resonantes

Hasta ahora, los diseños de filtros en los que nos hemos concentrado han empleado o condensadores o inductores, pero nunca ambos al mismo tiempo. A estas alturas, deberíamos saber que las combinaciones de L y C tenderán a resonar, y esta propiedad se puede explotar al diseñar circuitos de filtro de paso de banda y de parada de banda.

Los circuitos de la serie LC dan una impedancia mínima en resonancia, mientras que los circuitos LC ("tanque") en paralelo dan una impedancia máxima en su frecuencia de resonancia. Sabiendo esto, tenemos dos estrategias básicas para diseñar filtros de paso de banda o de parada de banda.

Para los filtros de paso de banda, las dos estrategias resonantes básicas son las siguientes:LC serie para pasar una señal, o LC en paralelo para acortar una señal. Los dos esquemas se compararán y simularán aquí:

Filtro de paso de banda resonante de la serie

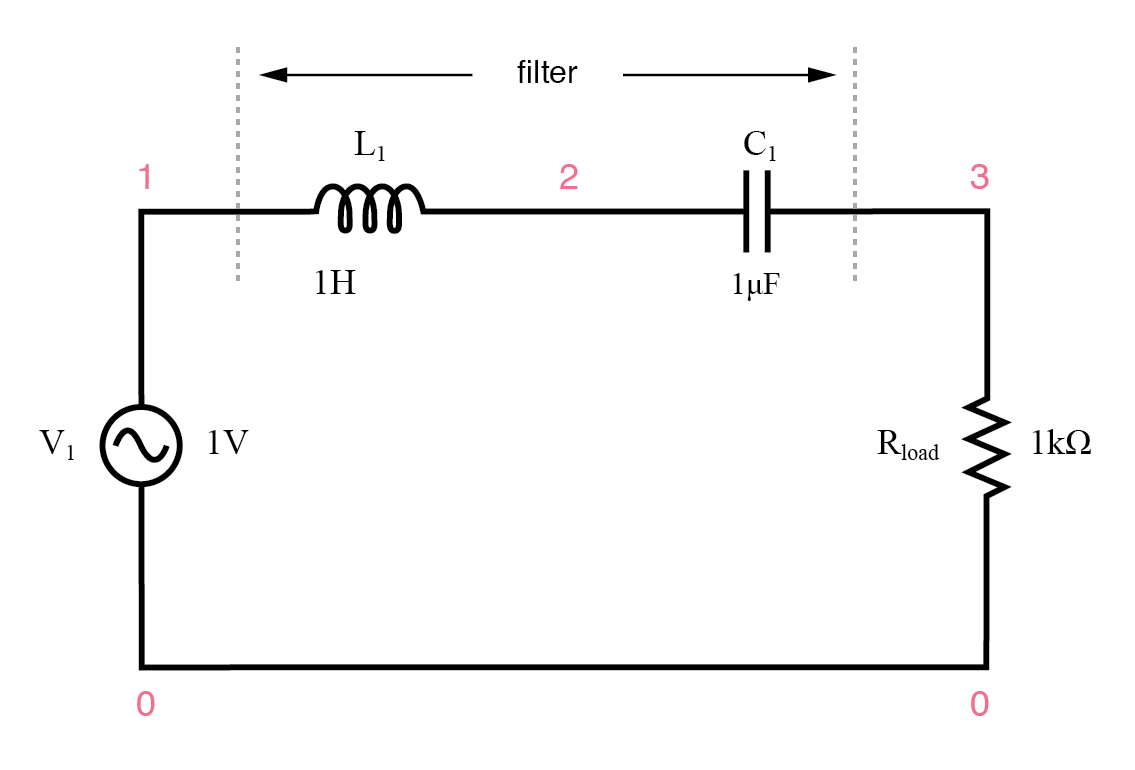
Filtro de paso de banda LC resonante de la serie.

Los componentes de la serie LC pasan la señal en resonancia y bloquean las señales de cualquier otra frecuencia para que no lleguen a la carga.

Filtro de paso de banda resonante de la serie

 v1 1 0 ac 1 pecado l1 1 2 1 c1 2 3 1u rload 3 0 1k .ac lin 20 50 250 .plot ac v (3) .fin 

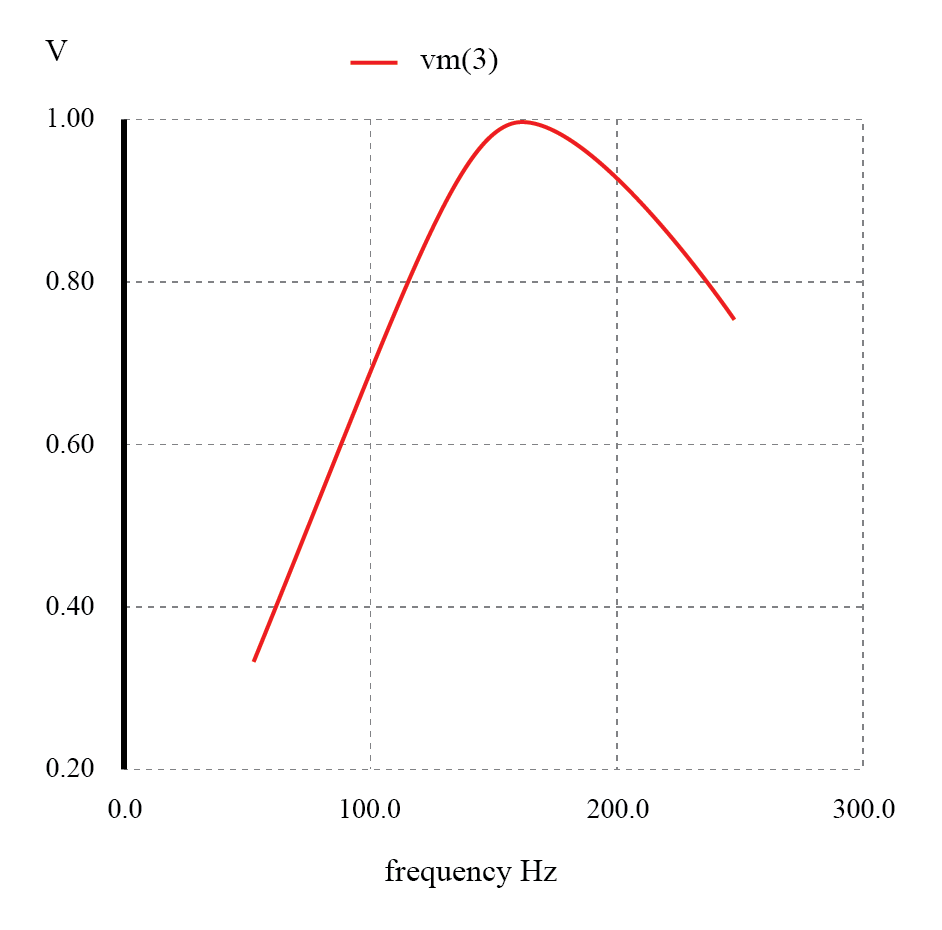
Filtro de paso de banda resonante en serie:picos de voltaje a una frecuencia de resonancia de 159,15 Hz.

Un par de puntos a tener en cuenta:observe cómo virtualmente no hay atenuación de señal dentro de la "banda de paso" (el rango de frecuencias cerca del pico de voltaje de carga), a diferencia de los filtros de paso de banda hechos de condensadores o inductores solamente.

Además, dado que este filtro funciona según el principio de resonancia LC en serie, cuya frecuencia de resonancia no se ve afectada por la resistencia del circuito, el valor de la resistencia de carga no sesgará la frecuencia máxima. Sin embargo, diferentes valores para la resistencia de carga se cambiar la "inclinación" del diagrama de Bode (la "selectividad" del filtro).

El otro estilo básico de filtros de paso de banda resonantes emplea un circuito de tanque (combinación LC en paralelo) para cortocircuitar las señales de frecuencia demasiado alta o demasiado baja para que no lleguen a la carga:

Filtro de paso de banda resonante paralelo

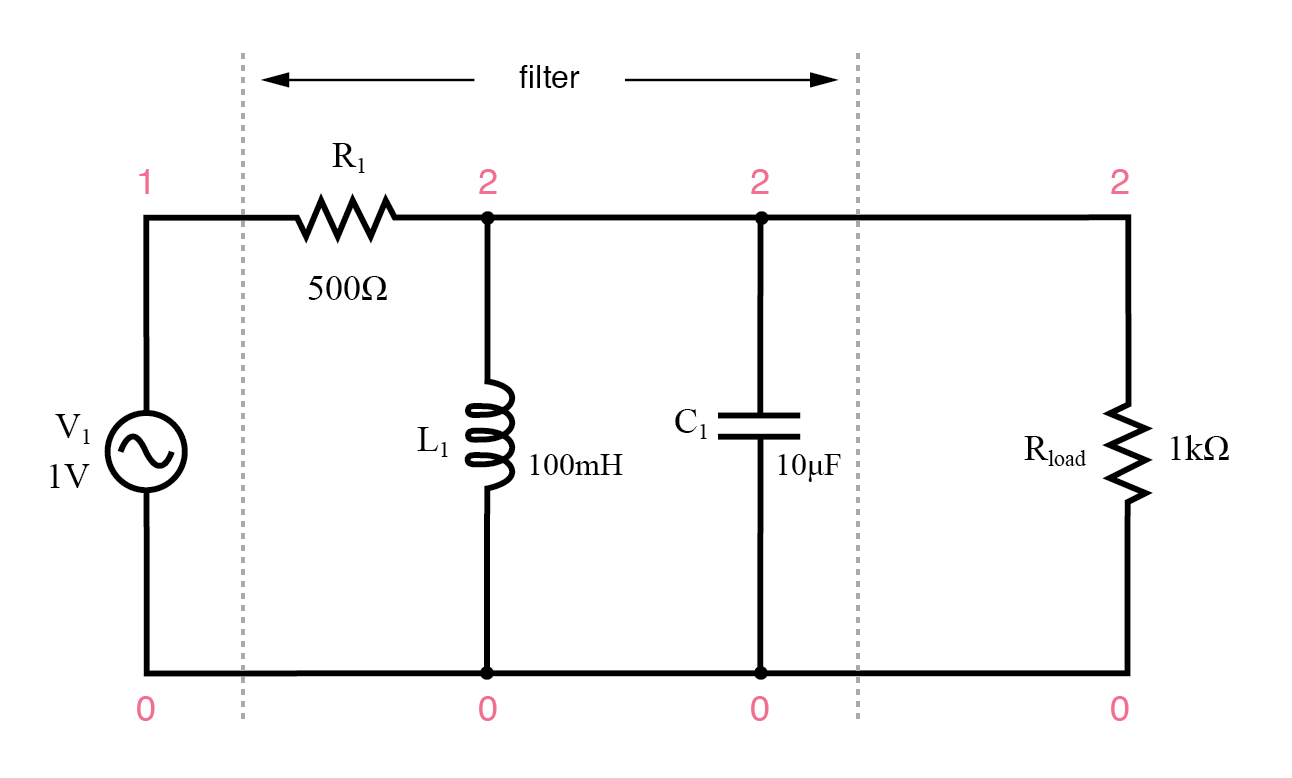
Filtro de paso de banda resonante paralelo.

El circuito del tanque tendrá mucha impedancia en resonancia, lo que permitirá que la señal llegue a la carga con una atenuación mínima. Sin embargo, por debajo o por encima de la frecuencia de resonancia, el circuito del tanque tendrá una impedancia baja, provocando un cortocircuito en la señal y dejando caer la mayor parte a través de la resistencia en serie R ₁ .

 filtro de paso de banda resonante paralelo v1 1 0 ac 1 pecado r1 1 2 500 l1 2 0 100m c1 2 0 10u rload 2 0 1k .ac lin 20 50 250 .plot ac v (2) .fin 

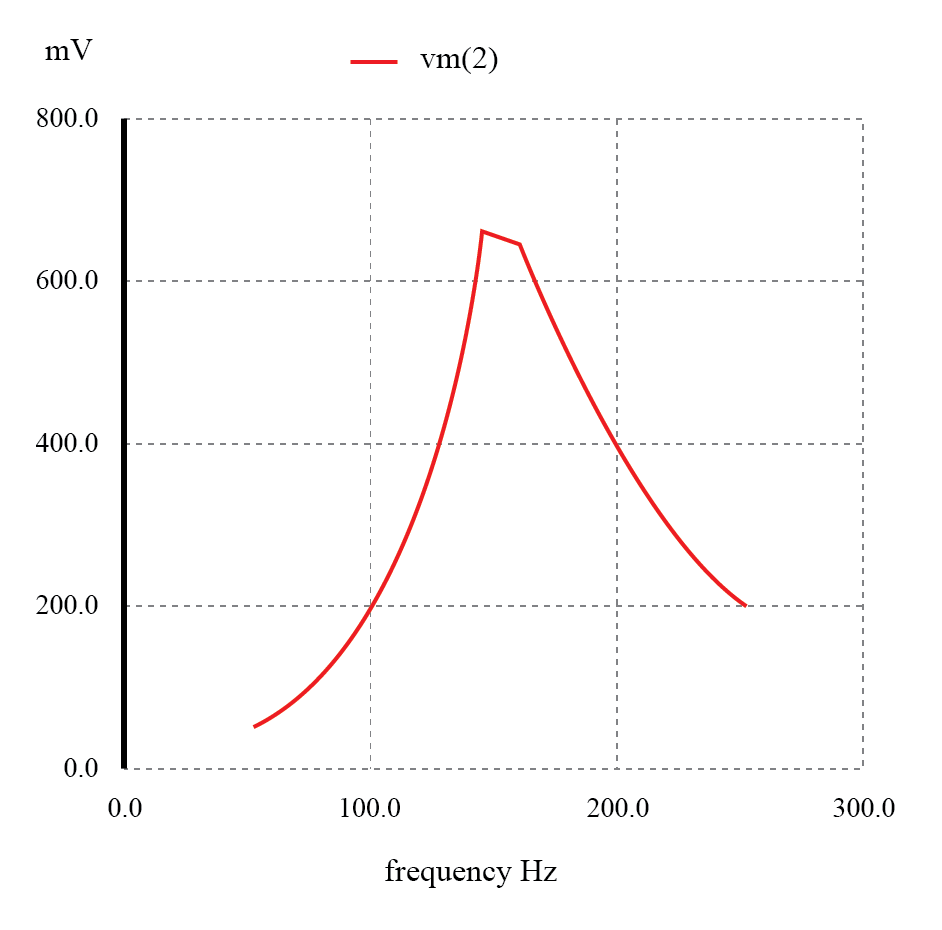
Filtro resonante paralelo:el voltaje alcanza una frecuencia resonante de 159,15 Hz.

Al igual que los diseños de filtro de paso bajo y paso alto que se basan en una resistencia en serie y un componente de "cortocircuito" paralelo para atenuar las frecuencias no deseadas, este circuito resonante nunca puede proporcionar voltaje de entrada (fuente) completo a la carga.

Esa resistencia en serie siempre caerá una cierta cantidad de voltaje siempre que haya una resistencia de carga conectada a la salida del filtro. Cabe señalar que esta forma de circuito de filtro de paso de banda es muy popular en los circuitos de sintonización de radio analógica, para seleccionar una frecuencia de radio particular entre las multitudes de frecuencias disponibles desde la antena.

En la mayoría de los circuitos sintonizadores de radio analógicos, el dial giratorio para la selección de la estación mueve un capacitor variable en un circuito tanque.

El condensador variable sintoniza el circuito del tanque del receptor de radio para seleccionar una de las muchas estaciones de transmisión.

El condensador variable y el inductor de núcleo de aire que se muestran en la fotografía de la Figura anterior de una radio simple comprenden los elementos principales en el filtro del circuito del tanque que se usa para discriminar la señal de una estación de radio de otra.

Así como podemos usar circuitos resonantes LC en serie y en paralelo para pasar solo aquellas frecuencias dentro de un cierto rango, también podemos usarlos para bloquear frecuencias dentro de un cierto rango, creando un filtro de parada de banda. Nuevamente, tenemos dos estrategias principales a seguir para hacer esto, usar resonancia en serie o en paralelo. Primero, veremos la variedad de series:

Filtro de parada de banda resonante de la serie

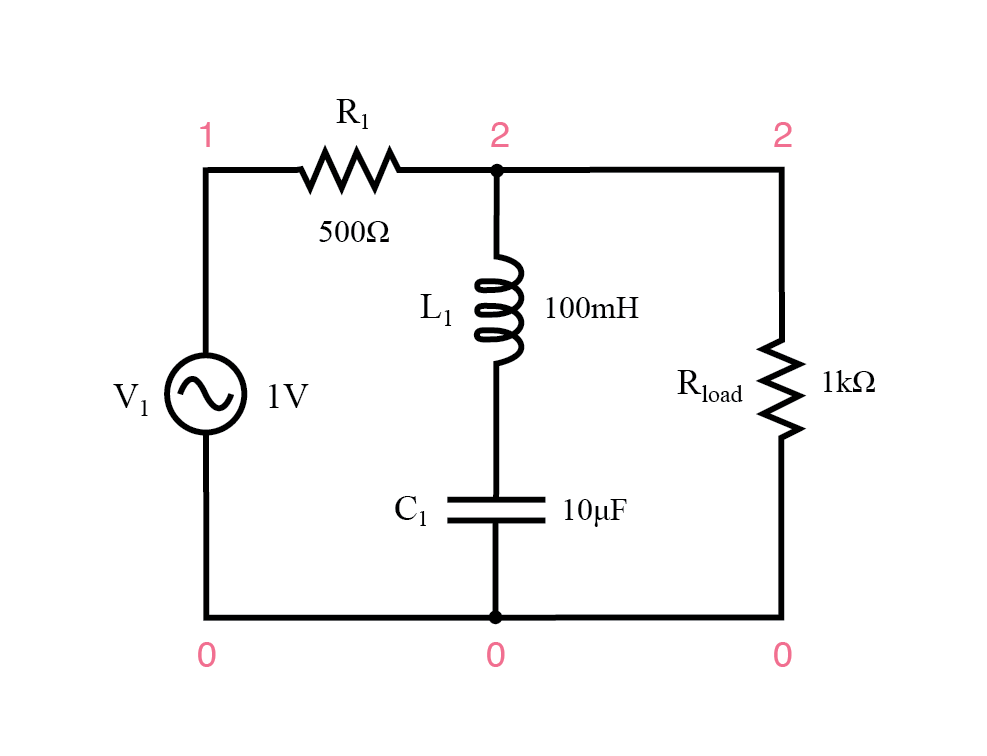
Filtro de parada de banda resonante de la serie.

Cuando la combinación de la serie LC alcanza resonancia, su muy baja impedancia corta la señal, dejándola caer a través de la resistencia R ₁ e impidiendo su paso a la carga.

Filtro de parada de banda resonante de la serie

 v1 1 0 ac 1 pecado r1 1 2 500 l1 2 3 100m c1 3 0 10u rload 2 0 1k .ac lin 20 70 230 .plot ac v (2) .fin 

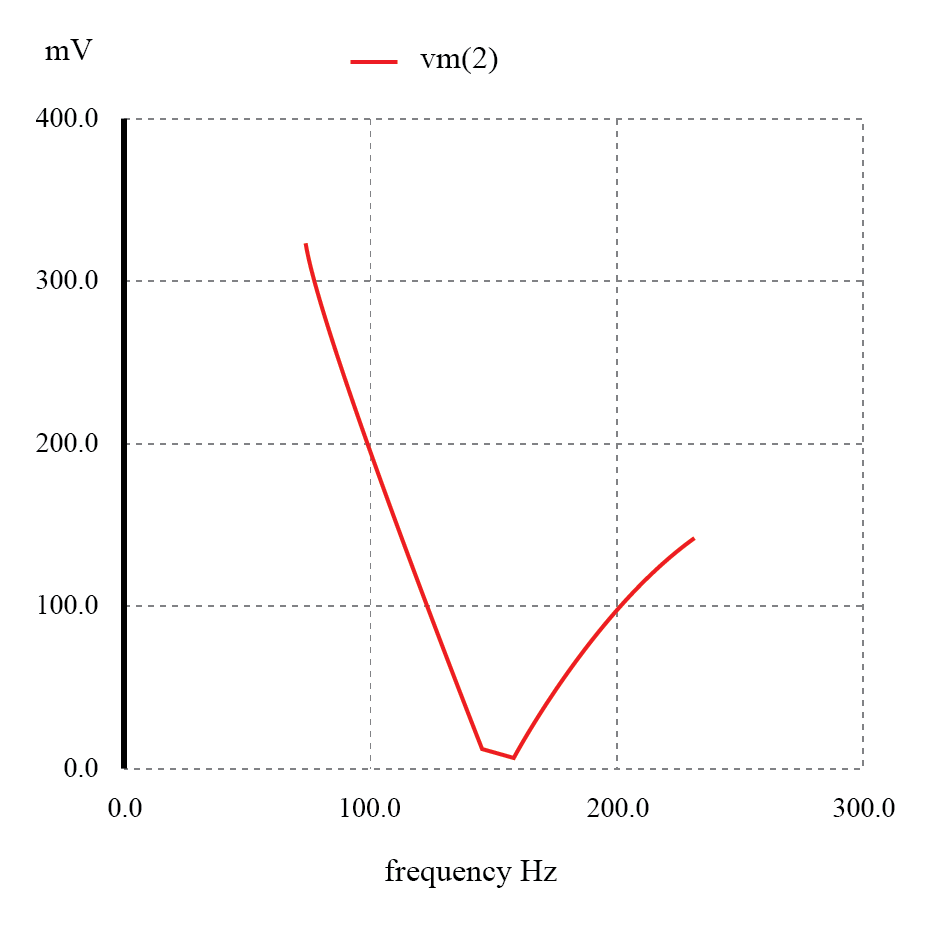
Filtro de parada de banda resonante en serie:frecuencia de muesca =frecuencia de resonancia LC (159,15 Hz).

A continuación, examinaremos el filtro de parada de banda resonante paralelo:

Filtro de parada de banda resonante paralelo

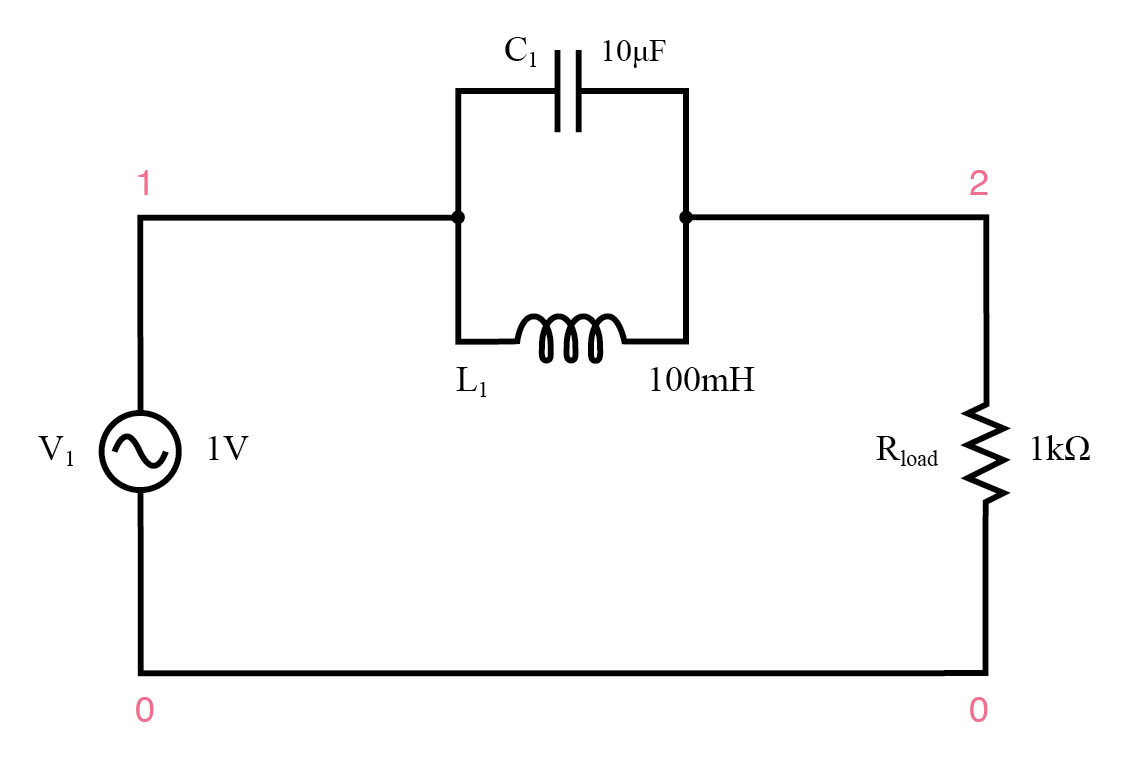
Filtro de parada de banda resonante paralelo.

Los componentes LC en paralelo presentan una alta impedancia a la frecuencia de resonancia, bloqueando así la señal de la carga a esa frecuencia. A la inversa, pasa señales a la carga en cualquier otra frecuencia.

 filtro de parada de banda resonante paralelo v1 1 0 ac 1 pecado l1 1 2 100m c1 1 2 10u rload 2 0 1k .ac lin 20100200 .plot ac v (2) .fin 

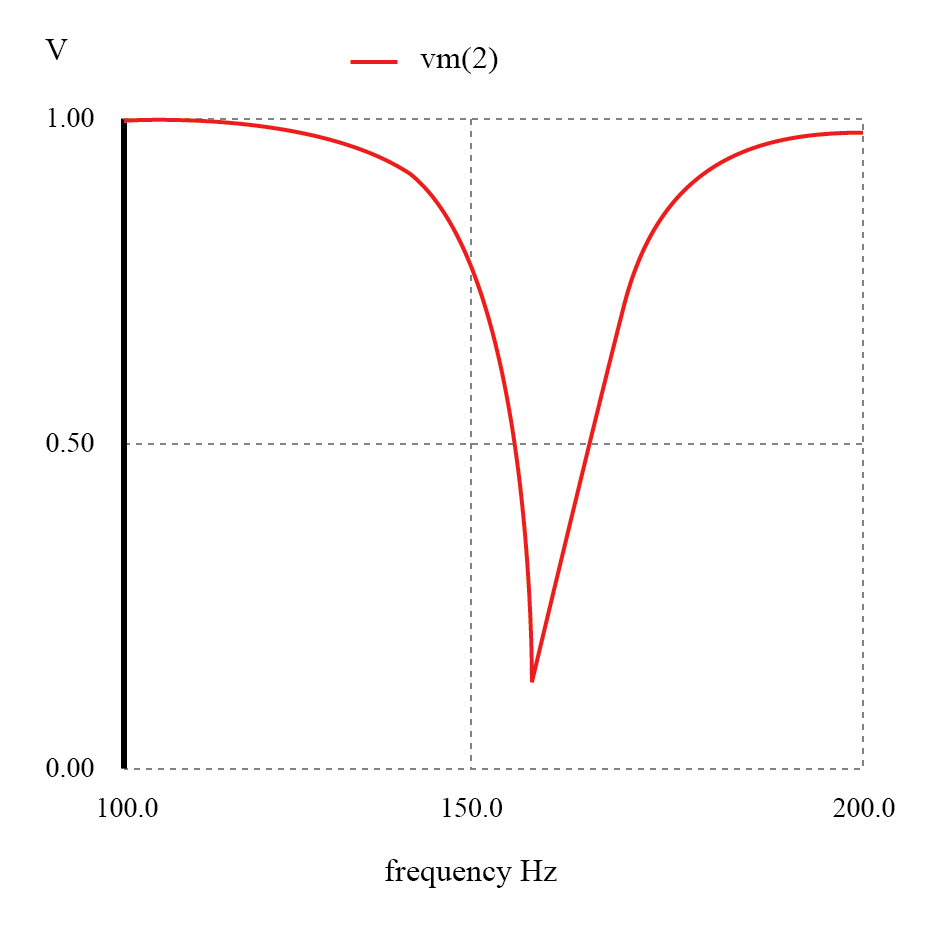
Filtro de parada de banda resonante paralelo:frecuencia de muesca =frecuencia de resonancia LC (159,15 Hz).

Una vez más, observe cómo la ausencia de una resistencia en serie hace que la atenuación sea mínima para todas las señales deseadas (pasadas). La amplitud en la frecuencia de la muesca, por otro lado, es muy baja. En otras palabras, este es un filtro muy "selectivo".

En todos estos diseños de filtros resonantes, la selectividad depende en gran medida de la "pureza" de la inductancia y capacitancia utilizadas. Si hay alguna resistencia parásita (especialmente probable en el inductor), esto disminuirá la capacidad del filtro para discriminar frecuencias con precisión, así como también introducirá efectos antirresonantes que sesgarán la frecuencia pico / muesca.

En este punto, conviene advertir a los que diseñan filtros de paso bajo y paso alto. Después de evaluar los diseños de filtros de paso bajo y paso alto RC y LR estándar, a un estudiante se le puede ocurrir que un diseño mejor y más efectivo de filtro de paso bajo o paso alto podría realizarse combinando elementos capacitivos e inductivos juntos como la figura siguiente.

Filtro de paso bajo inductivo capacitivo

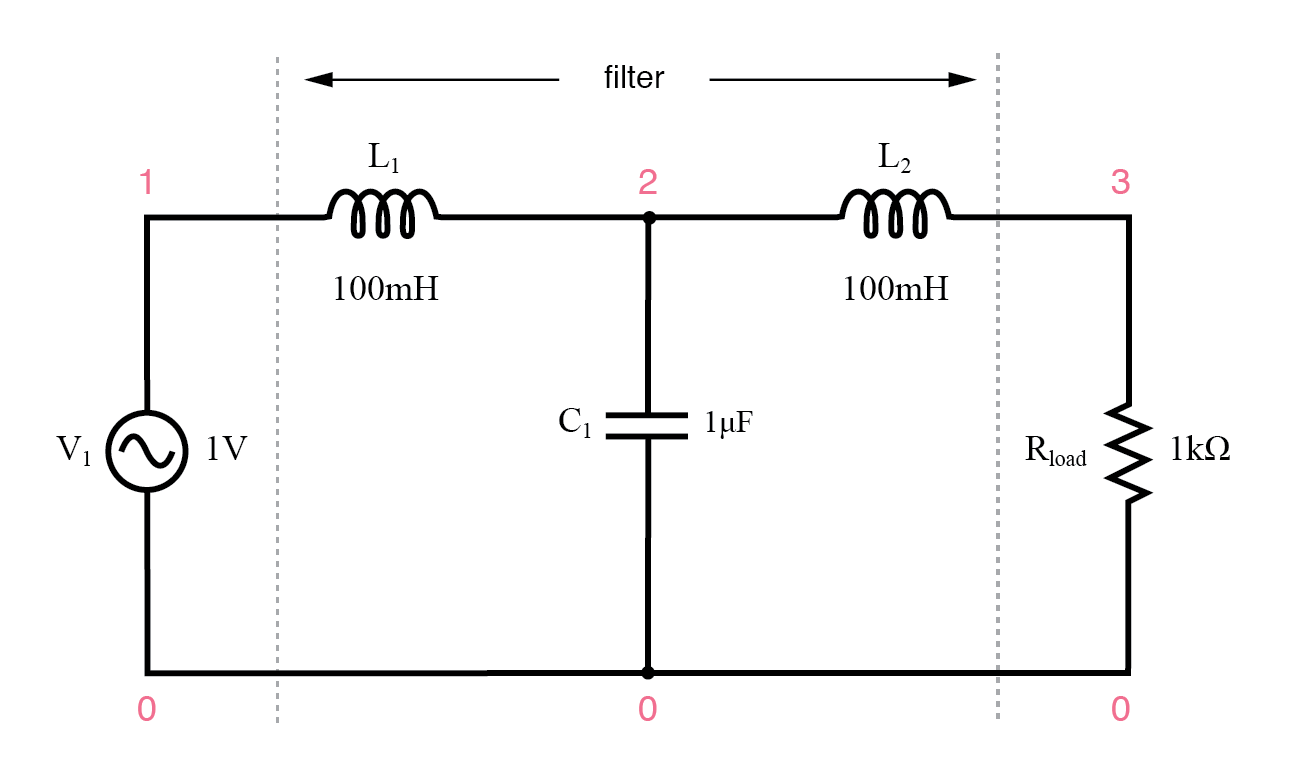
Filtro de paso bajo inductivo capacitivo.

Los inductores deben bloquear las altas frecuencias, mientras que el capacitor también debe cortocircuitar las altas frecuencias, ambos trabajando juntos para permitir que solo las señales de baja frecuencia lleguen a la carga.

Al principio, esta parece ser una buena estrategia y elimina la necesidad de una resistencia en serie. Sin embargo, el estudiante más perspicaz reconocerá que es probable que cualquier combinación de condensadores e inductores juntos en un circuito provoque efectos resonantes a una determinada frecuencia.

La resonancia, como hemos visto antes, puede provocar que sucedan cosas extrañas. Tracemos un análisis SPICE y veamos qué sucede en un amplio rango de frecuencias:

 filtro de paso bajo de lc v1 1 0 ac 1 pecado l1 1 2 100m c1 2 0 1u l2 2 3 100m rload 3 0 1k .ac lin 20100 1k .plot ac v (3) .fin 

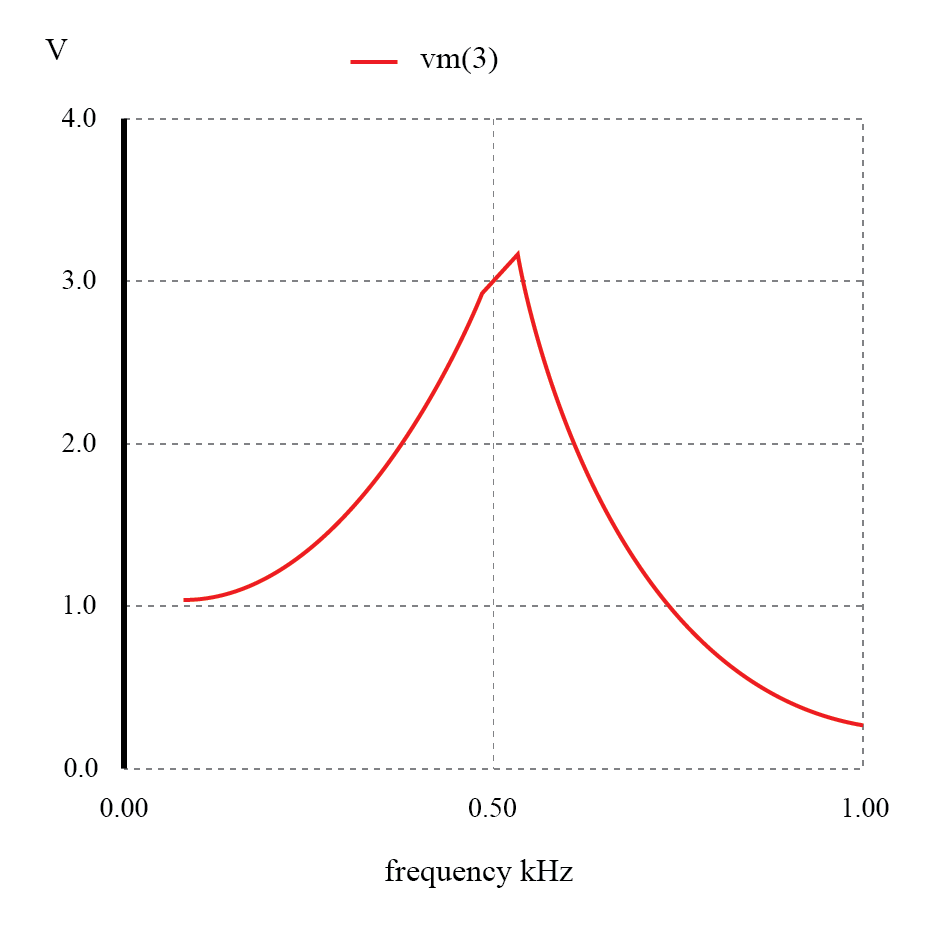
Respuesta inesperada del filtro de paso bajo L-C.

¡Lo que se suponía que era un filtro de paso bajo resulta ser un filtro de paso de banda con un pico en algún lugar alrededor de 526 Hz! La capacitancia y la inductancia en este circuito de filtro están alcanzando resonancia en ese punto, creando una gran caída de voltaje alrededor de C ₁ , que se ve en la carga, independientemente de L ₂ Influencia atenuante.

¡El voltaje de salida a la carga en este punto realmente excede el voltaje de entrada (fuente)! Un poco más de reflexión revela que si L ₁ y C ₂ están en resonancia, impondrán una carga muy pesada (impedancia muy baja) en la fuente de CA, lo que podría no ser bueno tampoco.

Ejecutaremos el mismo análisis nuevamente, solo que esta vez graficando C ₁ El voltaje, vm (2) en la figura siguiente, y la fuente de corriente, I (v1), junto con el voltaje de carga, vm (3):

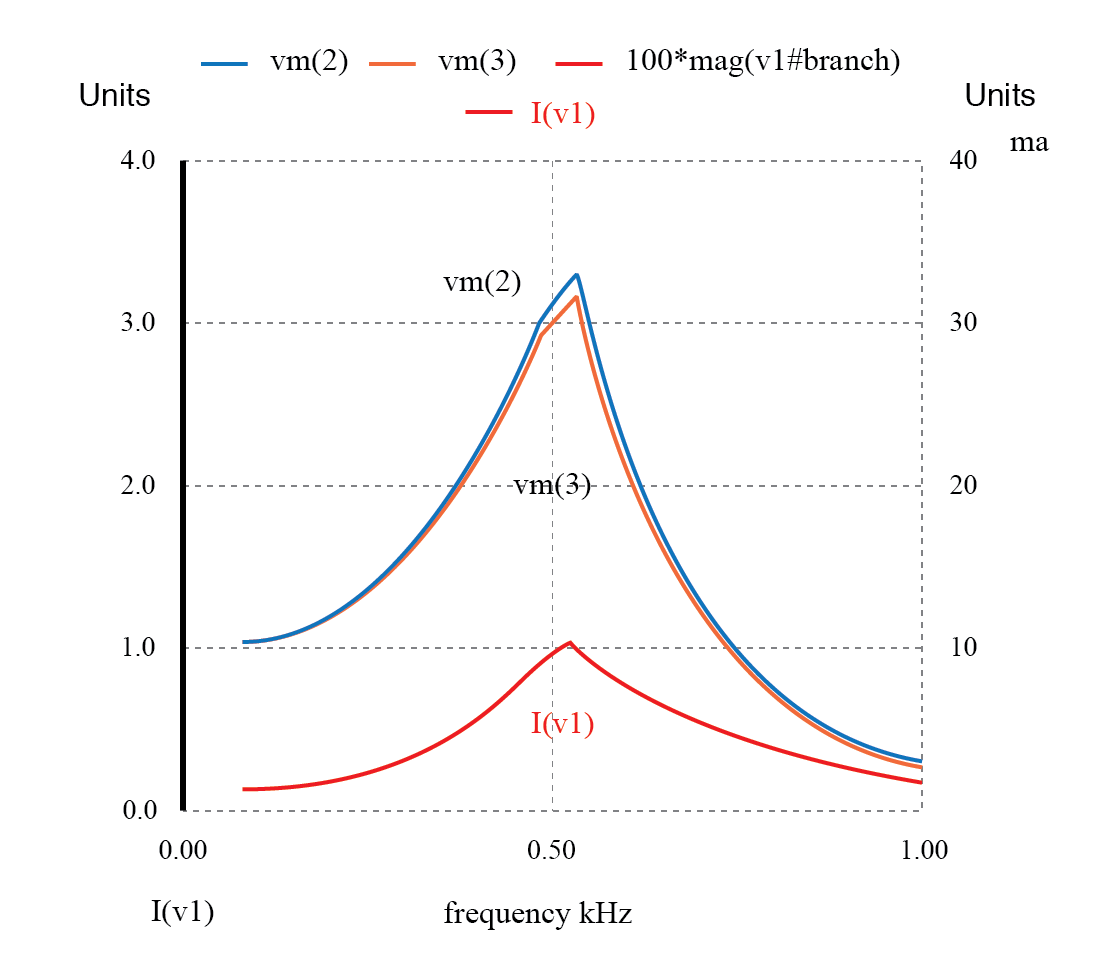
La corriente aumenta en la resonancia no deseada del filtro de paso bajo L-C.

Efectivamente, vemos el voltaje en C ₁ y el pico de corriente de la fuente a un punto alto a la misma frecuencia donde el voltaje de carga es máximo. Si esperábamos que este filtro proporcionara una función simple de paso bajo, es posible que nos decepcionen los resultados.

El problema es que un filtro L-C tiene una impedancia de entrada y una impedancia de salida que deben coincidir. La impedancia de la fuente de voltaje debe coincidir con la impedancia de entrada del filtro, y la impedancia de salida del filtro debe coincidir con "r _load ”Para una respuesta plana.

La impedancia de entrada y salida viene dada por la raíz cuadrada de (L / C).

Z =(L / C) ^1/2

Tomando los valores de los componentes de, podemos encontrar la impedancia del filtro y la requerida, R _g y R _cargar para que coincida.

Para L =100 mH, C =1µF Z =(L / C) ^1/2 =((100 mH) / (1 µF)) ^1/2 =316 Ω

En la siguiente figura, hemos agregado R _g =316 Ω al generador, y cambió la carga R _load de 1000 Ω a 316 Ω. Tenga en cuenta que si necesitáramos impulsar una carga de 1000 Ω, la relación L / C podría haberse ajustado para igualar esa resistencia.

Filtro de impedancia igualada

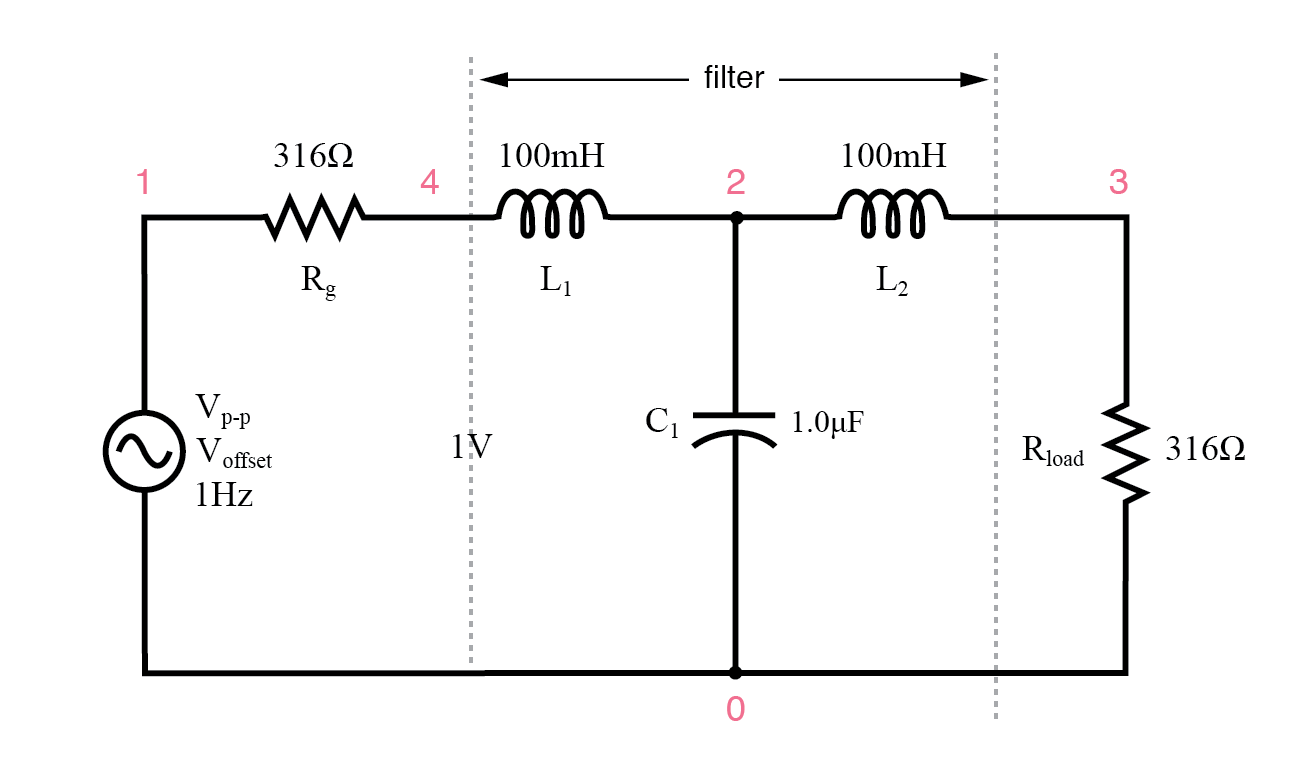
El circuito de la fuente y el filtro de paso bajo L-C coincidieron con la carga.

 Filtro de paso bajo adaptado a LC V1 1 0 ac 1 SIN Rg 1 4 316 L1 4 2 100m C1 2 0 1.0u L2 2 3 100m Carga 3 0 316 .ac lin 20100 1k .plot ac v (3) .fin 

La siguiente figura muestra la respuesta "plana" del filtro de paso bajo L-C cuando la fuente y la impedancia de carga coinciden con las impedancias de entrada y salida del filtro.

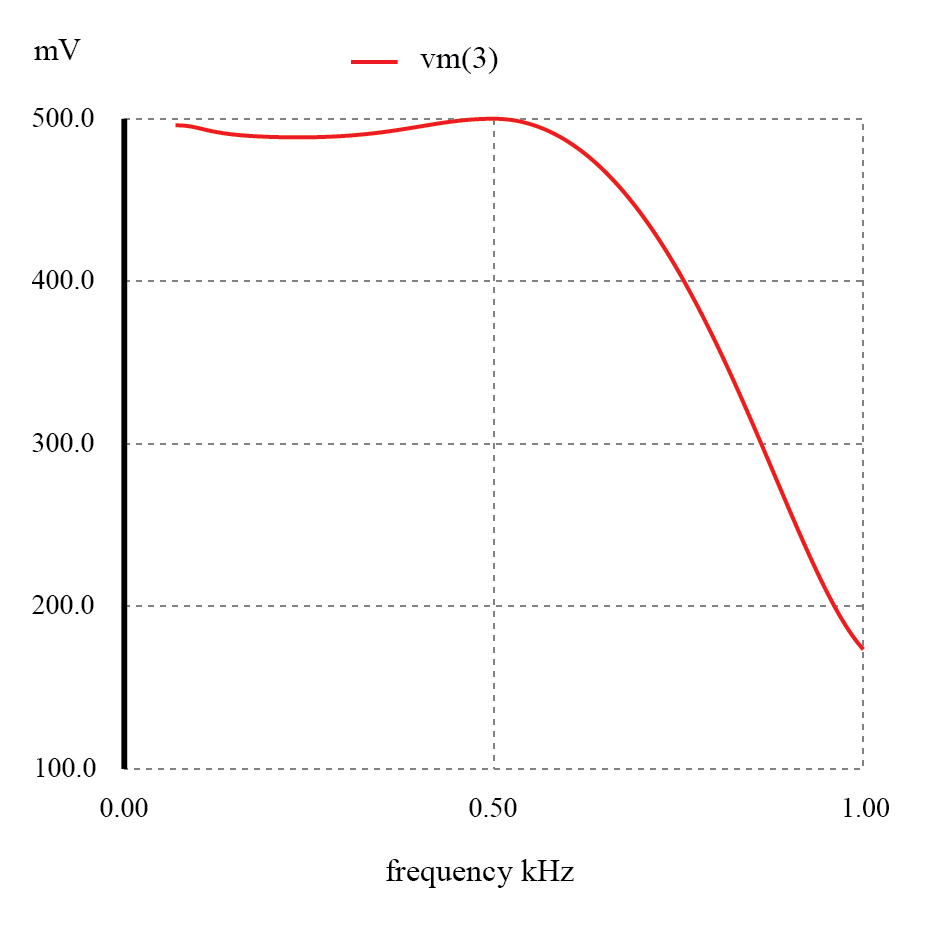
La respuesta del filtro de paso bajo L-C de impedancia igualada es casi plana hasta la frecuencia de corte.

El punto a destacar al comparar la respuesta del filtro no emparejado con el filtro emparejado es que la carga variable en el filtro produce un cambio considerable en el voltaje. Esta propiedad se aplica directamente a las fuentes de alimentación con filtro L-C:la regulación es pobre. El voltaje de la fuente de alimentación cambia con un cambio en la carga. Esto es indeseable.

Esta mala regulación de la carga se puede mitigar con un estrangulador oscilante . Esto es un estrangulamiento , inductor, diseñado para saturar cuando pasa una gran corriente continua a través de él.

Por saturar, queremos decir que la corriente CC crea un nivel "demasiado" alto de flujo en el núcleo magnético, de modo que el componente CA de la corriente no puede variar el flujo. Dado que la inducción es proporcional a dΦ / dt, la inductancia disminuye por la fuerte corriente continua.

La disminución de la inductancia disminuye la reactancia X _L . Disminuir la reactancia, reduce la caída de voltaje a través del inductor; así, aumentando el voltaje en la salida del filtro. Esto mejora la regulación de voltaje con respecto a cargas variables.

A pesar de la resonancia involuntaria, los filtros de paso bajo compuestos de condensadores e inductores se utilizan con frecuencia como etapas finales en las fuentes de alimentación de CA / CC para filtrar el voltaje de "ondulación" de CA no deseado de la CC convertida de CA.

¿Por qué ocurre esto, si este diseño de filtro en particular posee un punto de resonancia potencialmente problemático?

La respuesta radica en la selección de los tamaños de los componentes del filtro y las frecuencias que se encuentran en un convertidor de CA / CC (rectificador). Lo que estamos tratando de hacer en un filtro de fuente de alimentación de CA / CC es separar el voltaje de CC de una pequeña cantidad de voltaje de CA de frecuencia relativamente alta.

Los inductores y condensadores del filtro son generalmente bastante grandes (varios Henrys para los inductores y miles de µF para los condensadores son típicos), lo que hace que la frecuencia de resonancia del filtro sea muy, muy baja. DC, por supuesto, tiene una "frecuencia" de cero, por lo que no hay forma de que pueda hacer resonar un circuito LC.

El voltaje de ondulación, por otro lado, es un voltaje de CA no sinusoidal que consta de una frecuencia fundamental al menos dos veces la frecuencia del voltaje de CA convertido, con armónicos muchas veces más.

Para las fuentes de alimentación enchufables en la pared que funcionan con alimentación de CA de 60 Hz (60 Hz en Estados Unidos; 50 Hz en Europa), la frecuencia más baja que verá el filtro es de 120 Hz (100 Hz en Europa), que está muy por encima de su punto de resonancia. Por lo tanto, el punto de resonancia potencialmente problemático en un filtro de este tipo se evita por completo.

El siguiente análisis SPICE calcula la salida de voltaje (CA y CC) para dicho filtro, con fuentes de voltaje en serie CC y CA (120 Hz) que proporcionan una aproximación aproximada de la salida de frecuencia mixta de un convertidor CA / CC.

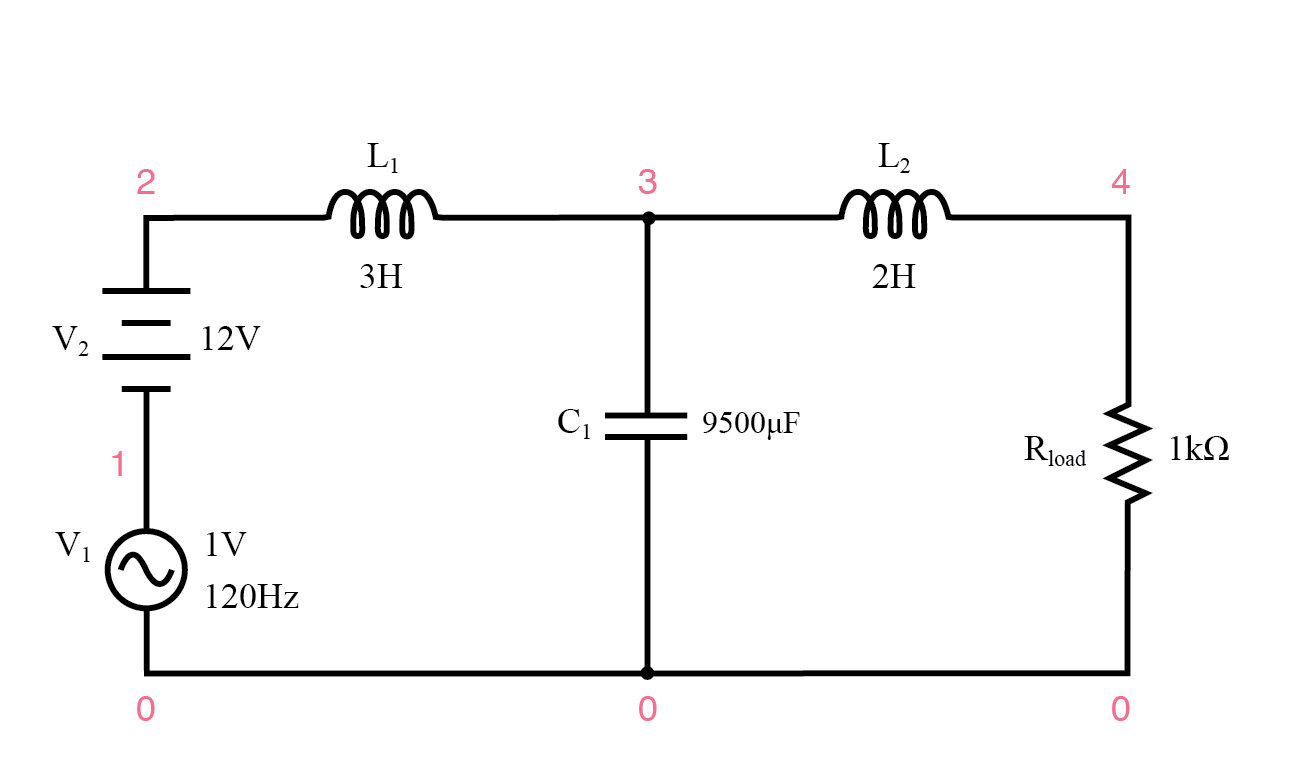
El filtro de la fuente de alimentación de CA / CC proporciona alimentación de CC "sin ondulaciones".

 El filtro de fuente de alimentación CA / CC proporciona alimentación CC "libre de ondulaciones" filtro de fuente de alimentación ac / dc v1 1 0 ac 1 pecado v2 2 1 dc l1 2 3 3 c1 3 0 9500u l2 3 4 2 rload 4 0 1k .dc v2 12 12 1 .ac lin 1120 120 .print dc v (4) .impresión ac v (4) .fin v2 v (4) 1.200E + 01 1.200E + 01 Voltaje CC con carga =12 voltios frecuencia v (4) 1.200E + 02 3.412E-05 Voltaje CA en carga =34.12 microvoltios 

Con 12 voltios CC completos en la carga y solo 34,12 µV de CA restantes de la fuente de CA de 1 voltio impuesta a través de la carga, este diseño de circuito demuestra ser un filtro de suministro de energía muy efectivo.

La lección aprendida aquí sobre los efectos resonantes también se aplica al diseño de filtros de paso alto que utilizan tanto condensadores como inductores. Siempre que las frecuencias deseadas y no deseadas estén bien a ambos lados del punto resonante, el filtro funcionará bien.

Pero si se aplica cualquier señal de magnitud significativa cercana a la frecuencia de resonancia a la entrada del filtro, ¡sucederán cosas extrañas!

REVISAR:

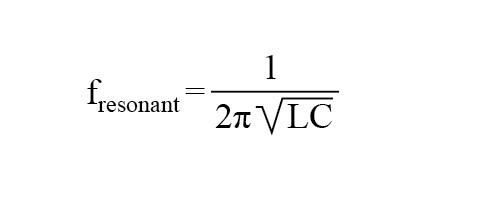
• Se pueden emplear combinaciones resonantes de capacitancia e inductancia para crear filtros de paso de banda y de parada de banda muy efectivos sin la necesidad de agregar resistencia en un circuito que disminuiría el paso de las frecuencias deseadas.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de resonancia
• Hoja de trabajo de circuitos de filtro pasivo