Circuitos de resistencia-inductor en serie

En la sección anterior, exploramos lo que sucedería en circuitos de CA simples de solo resistor y solo inductor. Ahora mezclaremos los dos componentes en forma de serie e investigaremos los efectos.

Ejemplo de circuito de inductor de resistencia en serie

Tome este circuito como ejemplo para trabajar:

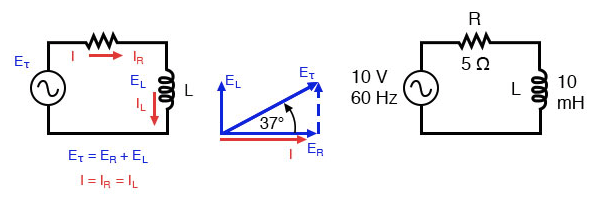
Circuito inductor de resistencia en serie:la corriente retrasa el voltaje aplicado de 0o a 90o.

La resistencia ofrecerá 5 Ω de resistencia a la corriente CA independientemente de la frecuencia, mientras que el inductor ofrecerá 3.7699 Ω de reactancia a la corriente CA a 60 Hz.

Debido a que la resistencia del resistor es un número real (5 Ω ∠ 0 °, o 5 + j0 Ω), y la reactancia del inductor es un número imaginario (3.7699 Ω ∠ 90 °, o 0 + j3.7699 Ω), el efecto combinado de los dos componentes serán una oposición a la corriente igual a la suma compleja de los dos números.

Esta oposición combinada será una combinación de vectores de resistencia y reactancia. Para expresar esta oposición de manera sucinta, necesitamos un término más completo para la oposición a la corriente que la resistencia o la reactancia por sí solas.

Este término se llama impedancia , su símbolo es Z, y también se expresa en la unidad de ohmios, al igual que la resistencia y la reactancia. En el ejemplo anterior, la impedancia total del circuito es:

Resistencia en la ley de Ohm

La impedancia está relacionada con el voltaje y la corriente tal como cabría esperar, de manera similar a la resistencia en la Ley de Ohm:

De hecho, esta es una forma mucho más completa de la ley de Ohm que la que se enseñó en la electrónica de CC (E =IR), al igual que la impedancia es una expresión de oposición al flujo de corriente mucho más completa que la resistencia. Cualquiera La resistencia y cualquier reactancia, por separado o en combinación (serie / paralelo), pueden y deben representarse como una sola impedancia en un circuito de CA.

Para calcular la corriente en el circuito anterior, primero debemos dar una referencia de ángulo de fase para la fuente de voltaje, que generalmente se supone que es cero. (Los ángulos de fase de la impedancia resistiva e inductiva son siempre 0 ° y + 90 °, respectivamente, independientemente de los ángulos de fase dados para voltaje o corriente).

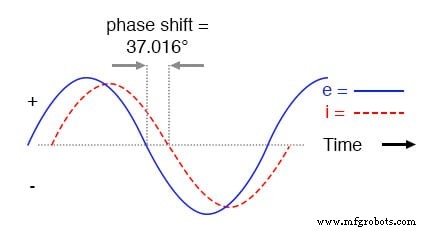
Al igual que con el circuito puramente inductivo, la onda de corriente va por detrás de la onda de voltaje (de la fuente), aunque esta vez el retraso no es tan grande:solo 37.016 ° en contraposición a un total de 90 ° como fue el caso en el circuito puramente inductivo .

La corriente retrasa el voltaje en un circuito L-R en serie.

Para el resistor y el inductor, las relaciones de fase entre el voltaje y la corriente no han cambiado. El voltaje a través de la resistencia está en fase (cambio de 0 °) con la corriente que lo atraviesa, y el voltaje a través del inductor está desfasado + 90 ° con la corriente que lo atraviesa. Podemos verificar esto matemáticamente:

El voltaje a través de la resistencia tiene exactamente el mismo ángulo de fase que la corriente a través de ella, lo que nos dice que E y yo estamos en fase (solo para la resistencia).

El voltaje a través del inductor tiene un ángulo de fase de 52,984 °, mientras que la corriente a través del inductor tiene un ángulo de fase de -37,016 °, una diferencia de exactamente 90 ° entre los dos. Esto nos dice que E e I todavía están desfasados ​​90 ° (solo para el inductor).

Utilice la ley de voltaje de Kirchhoff

También podemos demostrar matemáticamente que estos valores complejos se suman para formar el voltaje total, tal como lo predeciría la Ley del Voltaje de Kirchhoff:

Calcular usando SPICE

Comprobemos la validez de nuestros cálculos con SPICE:

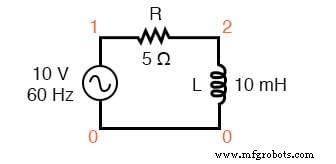
Circuito de especias:R-L.

 v1 1 0 ac 10 sin r1 1 2 5 l1 2 0 10m .ac lin 1 60 60 .imprimir ac v (1,2) v (2,0) i (v1) .print ac vp (1,2) vp (2,0) ip (v1) .fin 

 frecuencia v (1,2) v (2) i (v1) 6.000E + 01 7.985E + 00 6.020E + 00 1.597E + 00 frecuencia vp (1,2) vp (2) ip (v1) 6.000E + 01 -3.702E + 01 5.298E + 01 1.430E + 0 

Tenga en cuenta que, al igual que con los circuitos de CC, SPICE emite cifras de corriente como si fueran negativas (180 ° fuera de fase) con la tensión de alimentación. En lugar de un ángulo de fase de -37.016 °, obtenemos un ángulo de fase actual de 143 ° (-37 ° + 180 °).

Esto es simplemente una idiosincrasia de SPICE y no representa nada significativo en la simulación del circuito en sí. Observe cómo las lecturas de fase de voltaje de la resistencia y del inductor coinciden con nuestros cálculos (-37.02 ° y 52.98 °, respectivamente), tal como lo esperábamos.

Con todas estas cifras para realizar un seguimiento incluso para un circuito tan simple como este, sería beneficioso para nosotros utilizar el método de "tabla". La aplicación de una tabla a este circuito inductor-resistor en serie simple procedería como tal.

Primero, elabore una tabla para las cifras E / I / Z e inserte todos los valores de los componentes en estos términos (en otras palabras, no inserte los valores reales de resistencia o inductancia en ohmios y henries, respectivamente, en la tabla; más bien, conviértalos en figuras complejas de impedancia y escríbalas en):

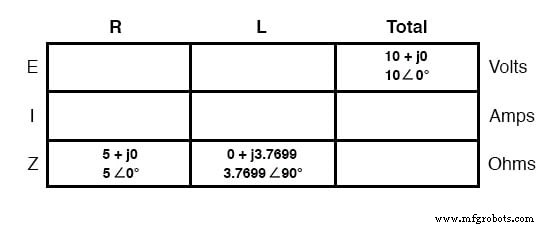
Aunque no es necesario, me resulta útil escribir ambos las formas rectangulares y polares de cada cantidad en la tabla. Si está utilizando una calculadora que tiene la capacidad de realizar operaciones aritméticas complejas sin la necesidad de conversión entre formas rectangulares y polares, entonces esta documentación adicional es completamente innecesaria.

Sin embargo, si se ve obligado a realizar operaciones aritméticas complejas "a mano" (suma y resta en forma rectangular y multiplicación y división en forma polar), escribir cada cantidad en ambas formas será realmente útil.

Ahora que nuestras cifras "dadas" están insertadas en sus respectivas ubicaciones en la tabla, podemos proceder como con DC:determine la impedancia total a partir de las impedancias individuales. Dado que este es un circuito en serie, sabemos que la oposición al flujo de corriente (resistencia o impedancia) se suma para formar la oposición total:

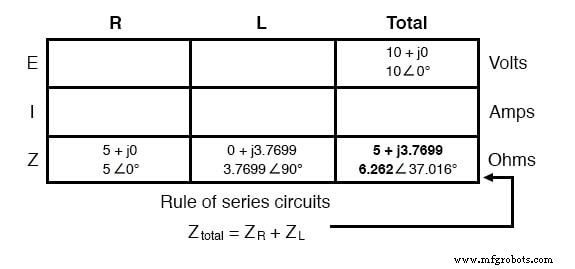
Ahora que conocemos el voltaje total y la impedancia total, podemos aplicar la Ley de Ohm (I =E / Z) para determinar la corriente total:

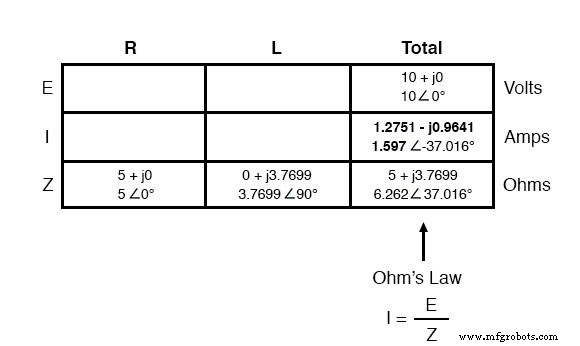
Al igual que con CC, la corriente total en un circuito de CA en serie es compartida por igual por todos los componentes. Esto sigue siendo cierto porque en un circuito en serie solo hay una ruta única para que fluya la corriente, por lo tanto, la velocidad de su flujo debe ser uniforme en todo momento. En consecuencia, podemos transferir las cifras de corriente a las columnas para el resistor y el inductor por igual:

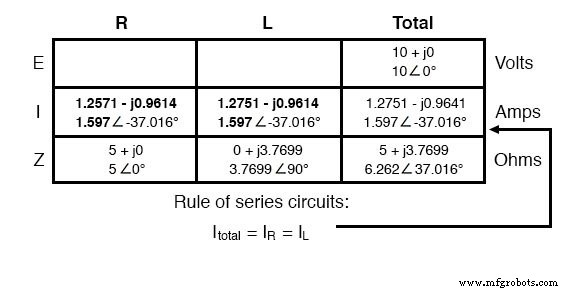
Ahora todo lo que queda por calcular es la caída de voltaje a través de la resistencia y el inductor, respectivamente. Esto se hace mediante el uso de la Ley de Ohm (E =IZ), aplicada verticalmente en cada columna de la tabla:

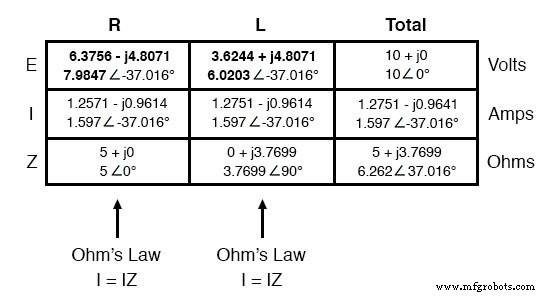
Y con eso, nuestra mesa está completa. Las mismas reglas exactas que aplicamos en el análisis de circuitos de CC se aplican también a los circuitos de CA, con la salvedad de que todas las cantidades deben representarse y calcularse en forma compleja en lugar de escalar.

Siempre que el cambio de fase esté representado correctamente en nuestros cálculos, no hay una diferencia fundamental en la forma en que abordamos el análisis básico del circuito de CA frente al de CC.

Ahora es un buen momento para revisar la relación entre estas cifras calculadas y las lecturas dadas por las mediciones reales de voltaje y corriente del instrumento.

Las cifras aquí que se relacionan directamente con las mediciones de la vida real son las de notación polar , no rectangular! En otras palabras, si conectara un voltímetro a través de la resistencia en este circuito, indicaría 7.9847 voltios, no 6.3756 (rectangular real) o 4.8071 (rectangular imaginaria) voltios.

Para describir esto en términos gráficos, los instrumentos de medición simplemente le dicen cuánto mide el vector para esa cantidad en particular (voltaje o corriente).

La notación rectangular, aunque conveniente para la suma y resta aritmética, es una forma de notación más abstracta que la polar en relación con las medidas del mundo real. Como dije antes, indicaré las formas polares y rectangulares de cada cantidad en mis tablas de circuitos de CA simplemente por conveniencia del cálculo matemático.

Esto no es absolutamente necesario, pero puede ser útil para quienes lo sigan sin el beneficio de una calculadora avanzada. Si nos limitáramos al uso de una sola forma de notación, la mejor opción sería polar, porque es la única que puede correlacionarse directamente con medidas reales.

Se puede calcular la impedancia (Z) de un circuito en serie R-L, dada la resistencia (R) y la reactancia inductiva (XL). Dado que E =IR, E =IXL y E =IZ, la resistencia, la reactancia y la impedancia son proporcionales al voltaje, respectivamente. Por lo tanto, el diagrama de fasores de voltaje se puede reemplazar por un diagrama de impedancia similar.

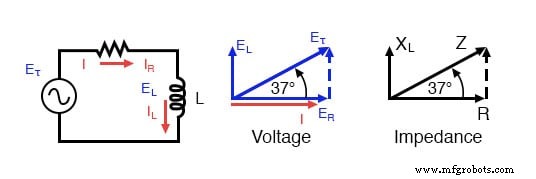
Serie:diagrama de fasor de impedancia del circuito R-L.

Ejemplo: Dado:Una resistencia de 40 Ω en serie con un inductor de 79,58 milihenrios. Encuentre la impedancia a 60 hercios.

 XL =2πfL XL =2π · 60 · 79,58 × 10-3 XL =30 Ω Z =R + jXL Z =40 + j30 | Z | =raíz cuadrada (402 + 302) =50 Ω ∠Z =arcotangente (30/40) =36,87 ° Z =40 + j30 =50∠36,87 ° 

REVISAR:

• Impedancia es la medida total de oposición a la corriente eléctrica y es la suma compleja (vectorial) de la resistencia ("real") y la reactancia ("imaginaria"). Está simbolizado por la letra "Z" y se mide en ohmios, al igual que la resistencia (R) y la reactancia (X).
• Las impedancias (Z) se gestionan como las resistencias (R) en el análisis de circuitos en serie:las impedancias en serie se suman para formar la impedancia total. ¡Solo asegúrese de realizar todos los cálculos en forma compleja (no escalar)! Z _Total =Z ₁ + Z ₂ +. . . Z _n
• Una impedancia puramente resistiva siempre tendrá un ángulo de fase de exactamente 0 ° (ZR =R Ω ∠ 0 °).
• Una impedancia puramente inductiva siempre tendrá un ángulo de fase de exactamente + 90 ° (ZL =XL Ω ∠ 90 °).
• Ley de Ohm para circuitos de CA:E =IZ; I =E / Z; Z =E / I
• Cuando los resistores y los inductores se mezclan en circuitos, la impedancia total tendrá un ángulo de fase entre 0 ° y + 90 °. La corriente del circuito tendrá un ángulo de fase entre 0 ° y -90 °.
• Los circuitos de CA en serie exhiben las mismas propiedades fundamentales que los circuitos de CC en serie:la corriente es uniforme en todo el circuito, las caídas de voltaje se suman para formar el voltaje total y las impedancias se suman para formar la impedancia total.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de inductores
• Hoja de trabajo de resistencia, reactancia e impedancia
• Hoja de trabajo de reactancia inductiva