Impedancia característica

Los alambres paralelos de longitud infinita

Supongamos, sin embargo, que tuviéramos un conjunto de cables paralelos de infinito de longitud, sin lámpara al final. ¿Qué pasaría cuando cerramos el interruptor? Dado que ya no hay carga al final de los cables, este circuito está abierto. ¿No habría ninguna corriente? (Figura siguiente)

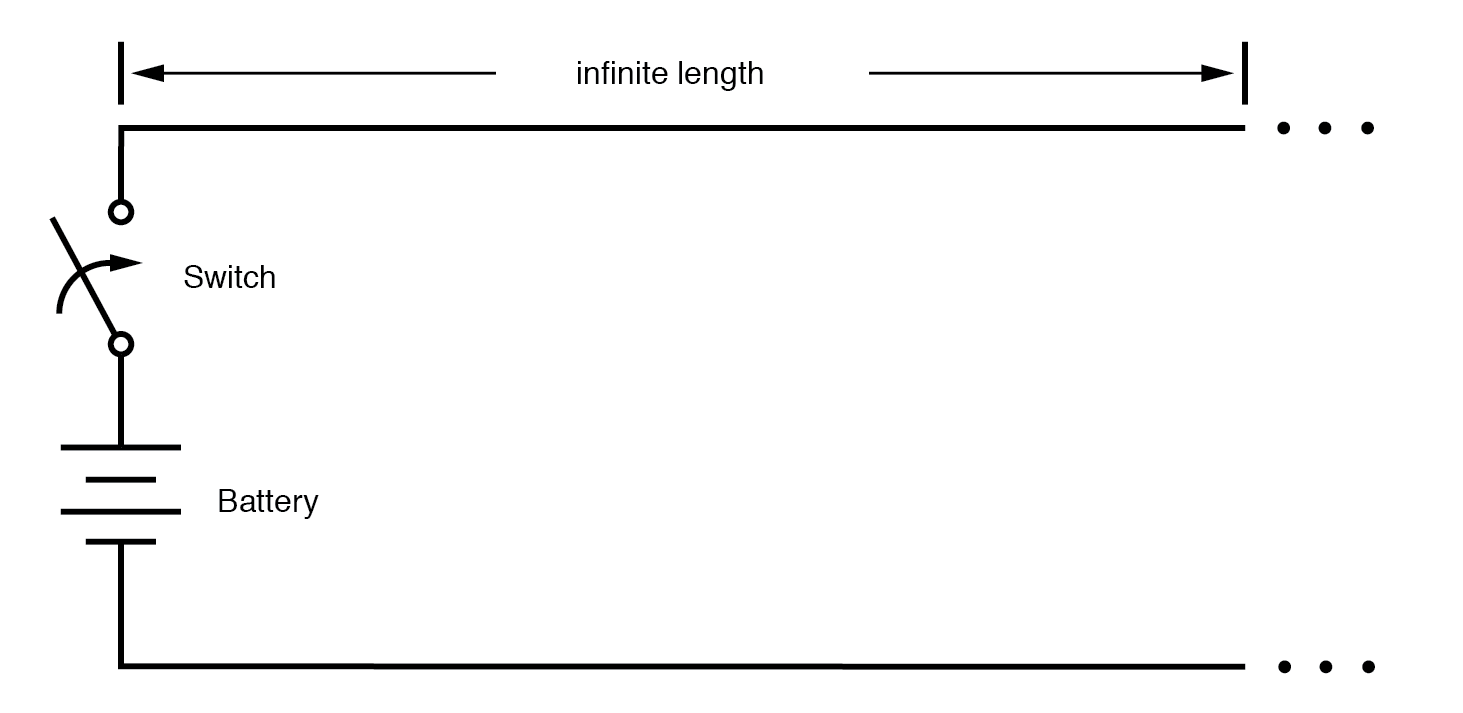
Conduciendo una línea de transmisión infinita.

A pesar de poder evitar la resistencia de los cables mediante el uso de superconductores en este "experimento mental", no podemos eliminar la capacitancia a lo largo de la longitud de los cables. Cualquiera un par de conductores separados por un medio aislante crea capacitancia entre esos conductores:(Figura siguiente)

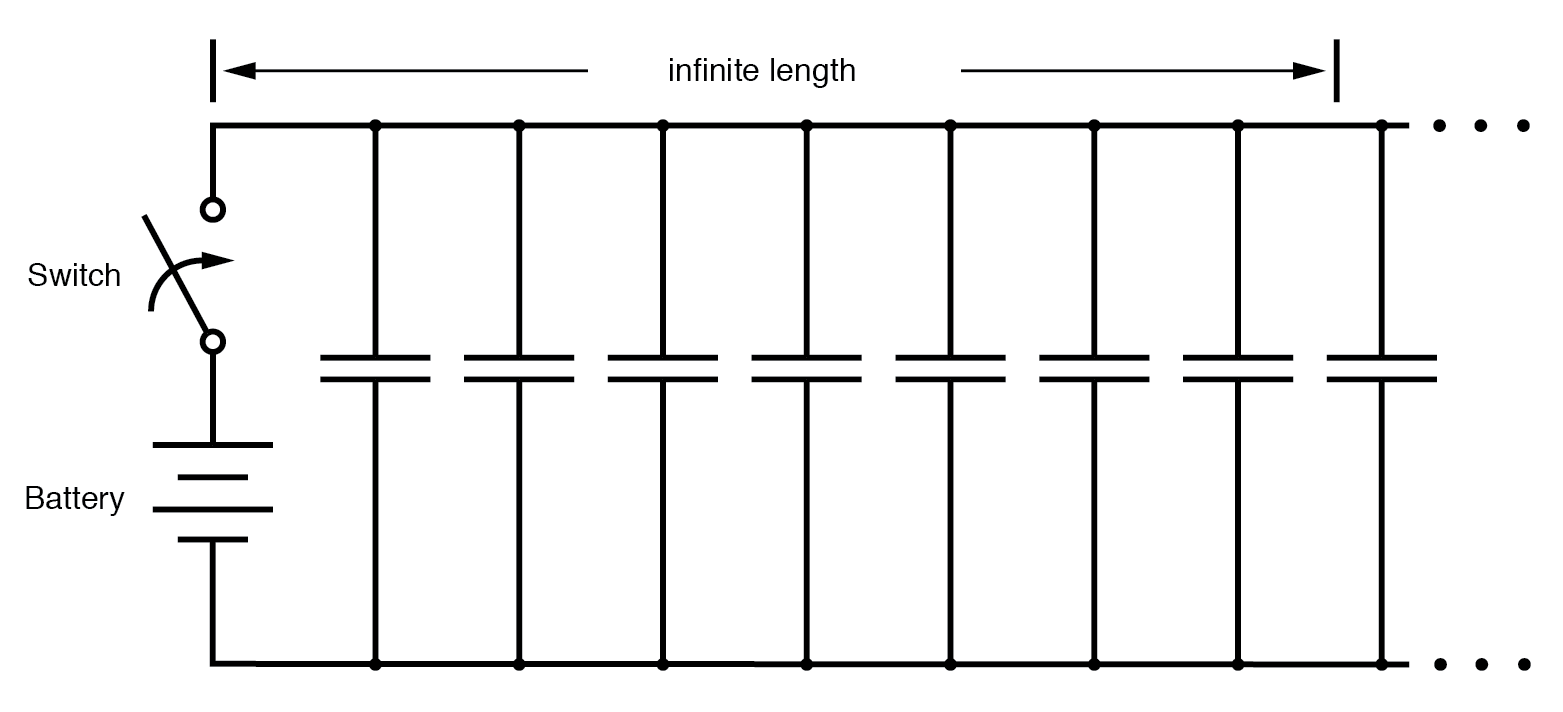
Circuito equivalente que muestra capacitancia parásita entre conductores.

El voltaje aplicado entre dos conductores crea un campo eléctrico entre esos conductores. La energía se almacena en este campo eléctrico y este almacenamiento de energía da como resultado una oposición al cambio de voltaje. La reacción de una capacitancia frente a cambios en el voltaje se describe mediante la ecuación i =C (de / dt), que nos dice que la corriente se consumirá de manera proporcional a la tasa de cambio del voltaje a lo largo del tiempo. Por lo tanto, cuando el interruptor está cerrado, la capacitancia entre los conductores reaccionará contra el aumento repentino de voltaje cargándose y extrayendo corriente de la fuente. Según la ecuación, un aumento instantáneo en el voltaje aplicado (producido por el cierre perfecto del interruptor) da lugar a una corriente de carga infinita.

Capacitancia e inductancia

Sin embargo, la corriente consumida por un par de cables paralelos no será infinita, porque existe una serie de impedancia a lo largo de los cables debido a la inductancia. (Imagen siguiente) Recuerde que la corriente a través de cualquiera El conductor desarrolla un campo magnético de magnitud proporcional. La energía se almacena en este campo magnético, (Figura siguiente) y este almacenamiento de energía resulta en una oposición al cambio en la corriente. Cada cable desarrolla un campo magnético a medida que transporta corriente de carga para la capacitancia entre los cables y, al hacerlo, reduce el voltaje de acuerdo con la ecuación de inductancia e =L (di / dt). Esta caída de voltaje limita la tasa de cambio de voltaje a través de la capacitancia distribuida, evitando que la corriente alcance una magnitud infinita:

Circuito equivalente que muestra inductancia y capacitancia parásita.

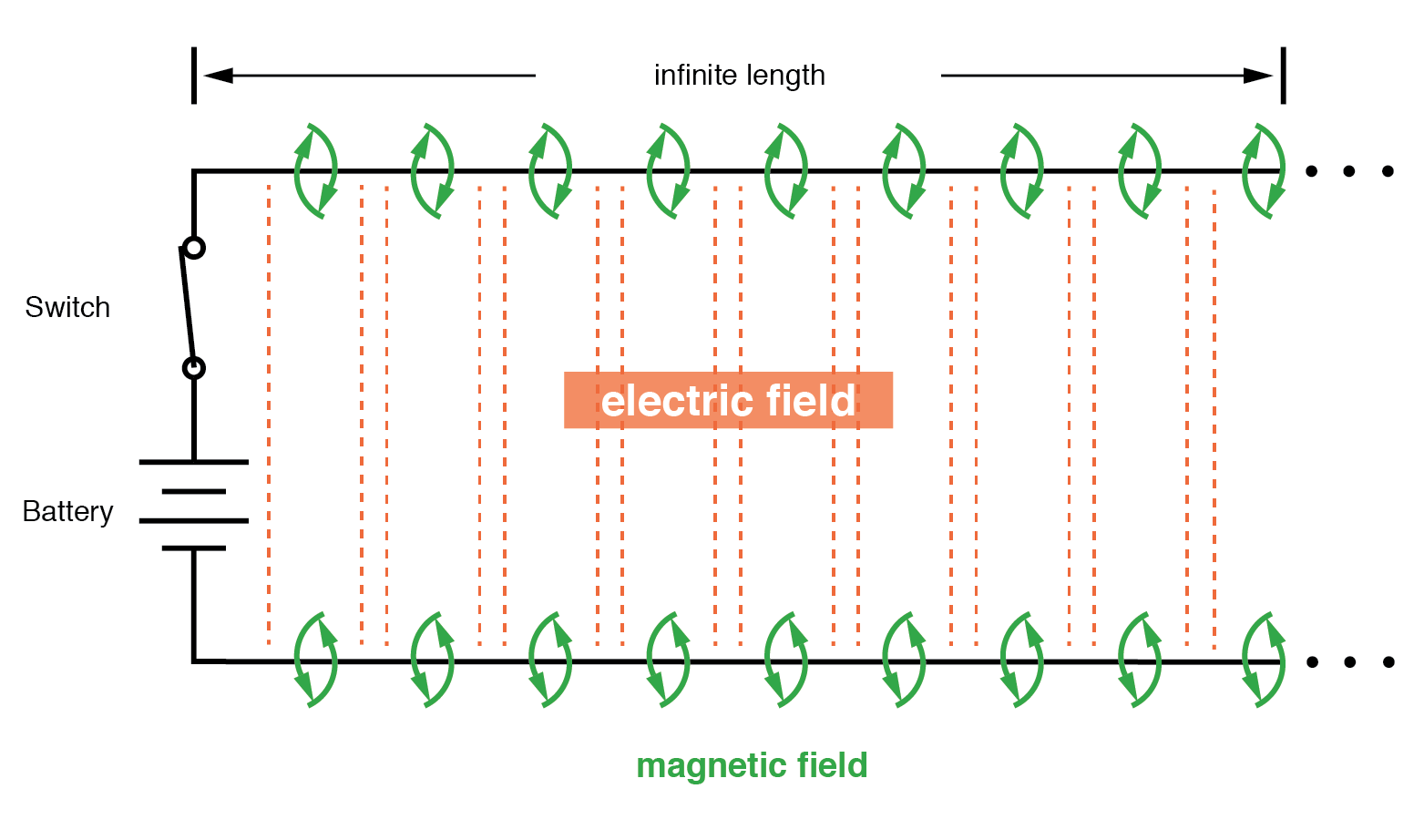
El voltaje carga la capacitancia, la corriente carga la inductancia.

Debido a que los portadores de carga eléctrica en los dos cables transfieren el movimiento entre sí a casi la velocidad de la luz, el "frente de onda" del cambio de voltaje y corriente se propagará a lo largo de los cables a esa misma velocidad, lo que dará como resultado la distribución distribuida capacitancia e inductancia cargándose progresivamente a voltaje y corriente completos, respectivamente, así:

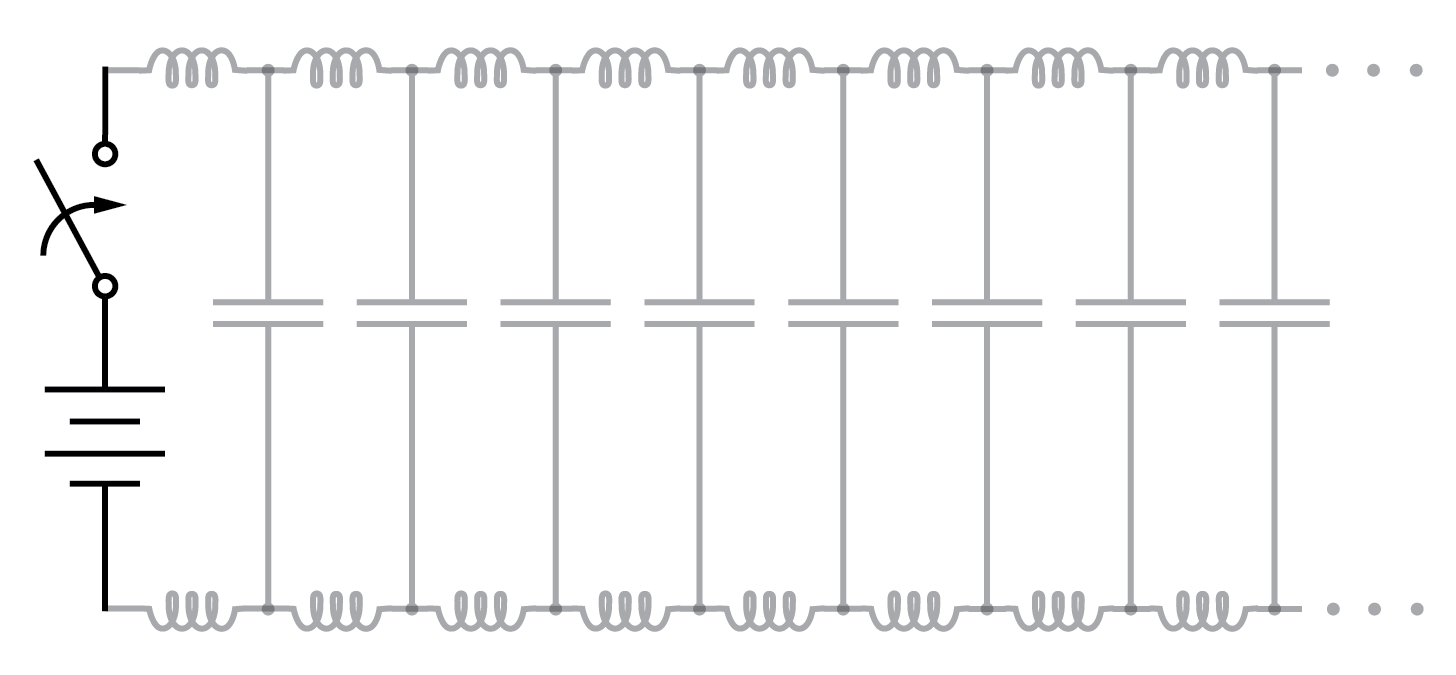
Línea de transmisión descargada.

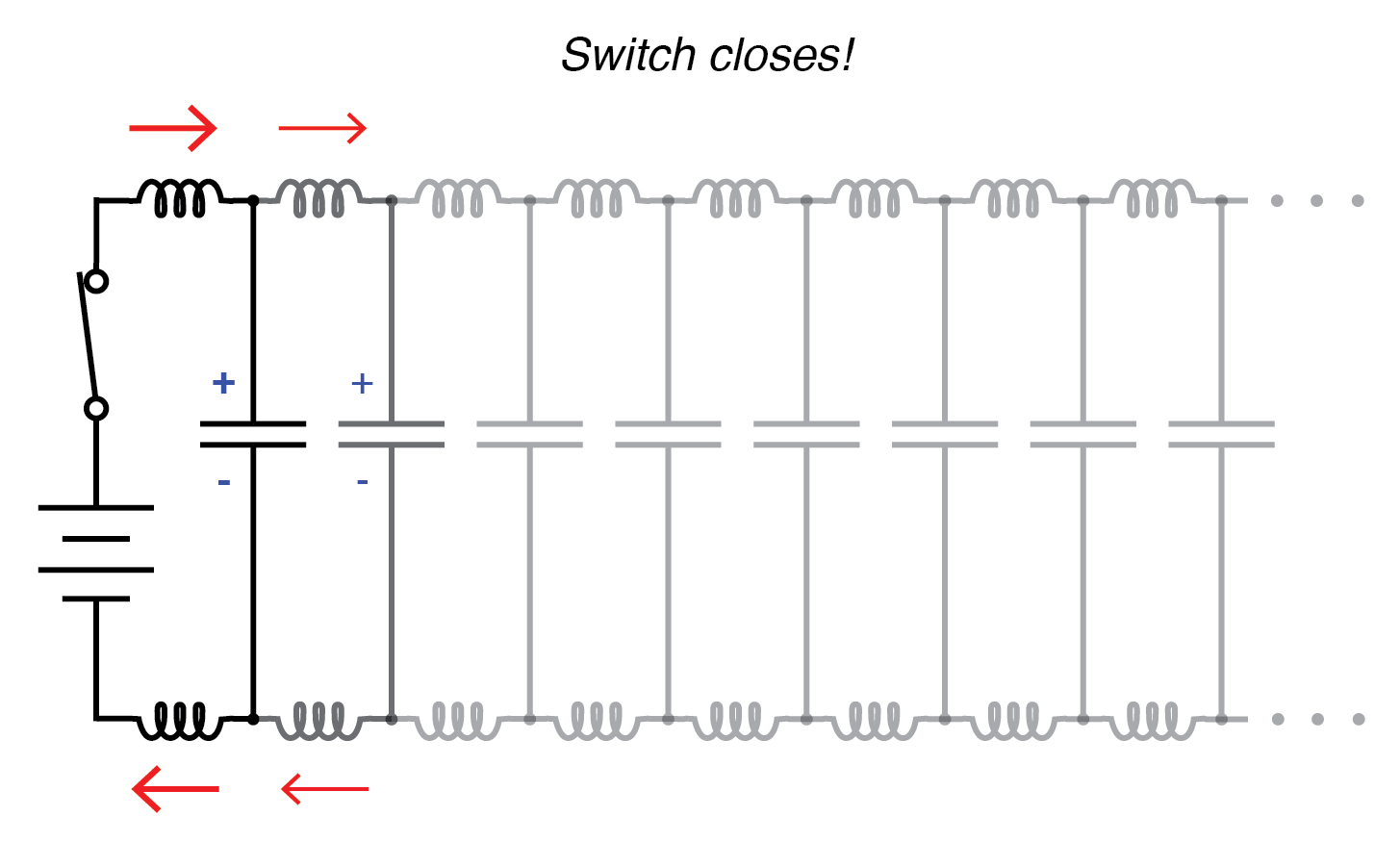
Comience la propagación de ondas.

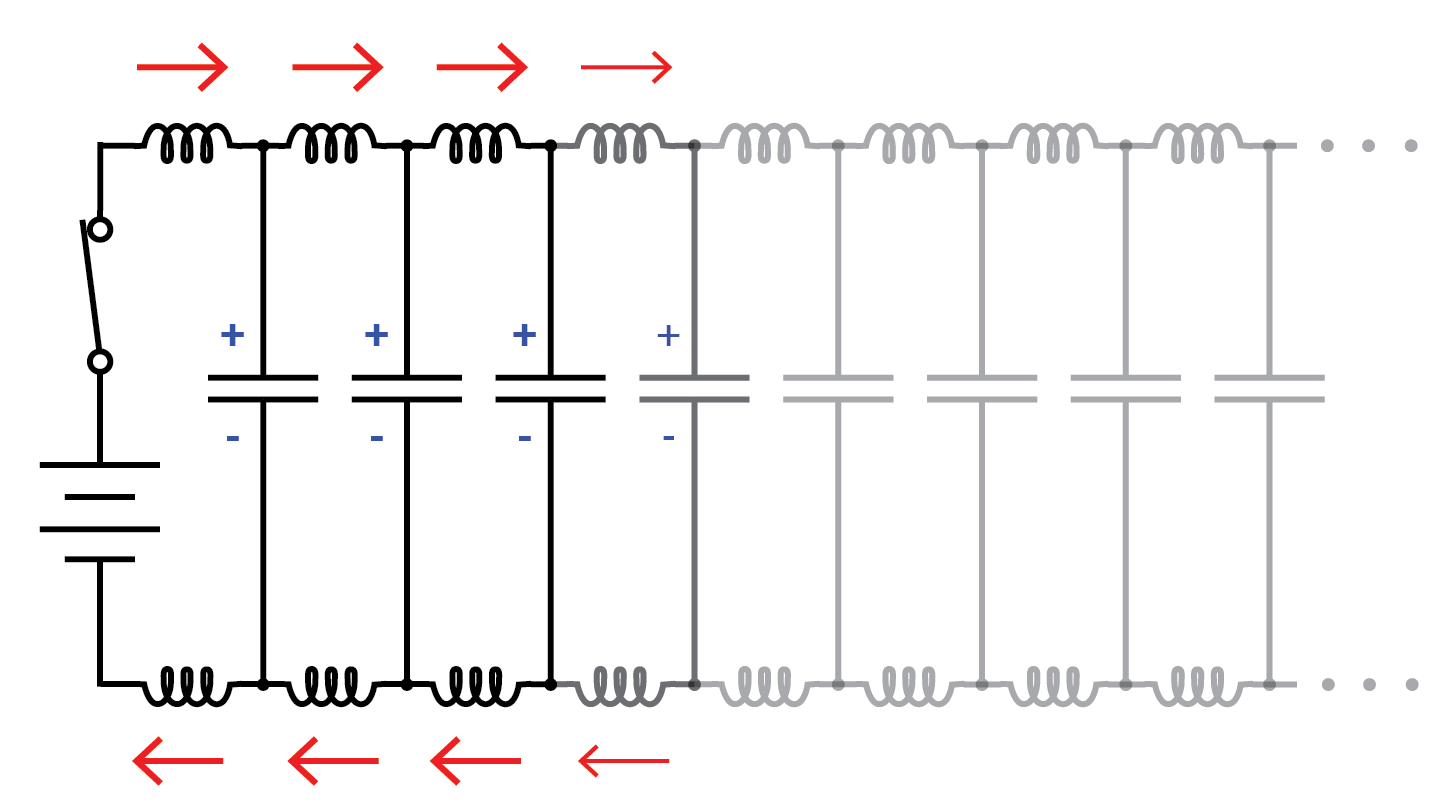
Continuar con la propagación de ondas.

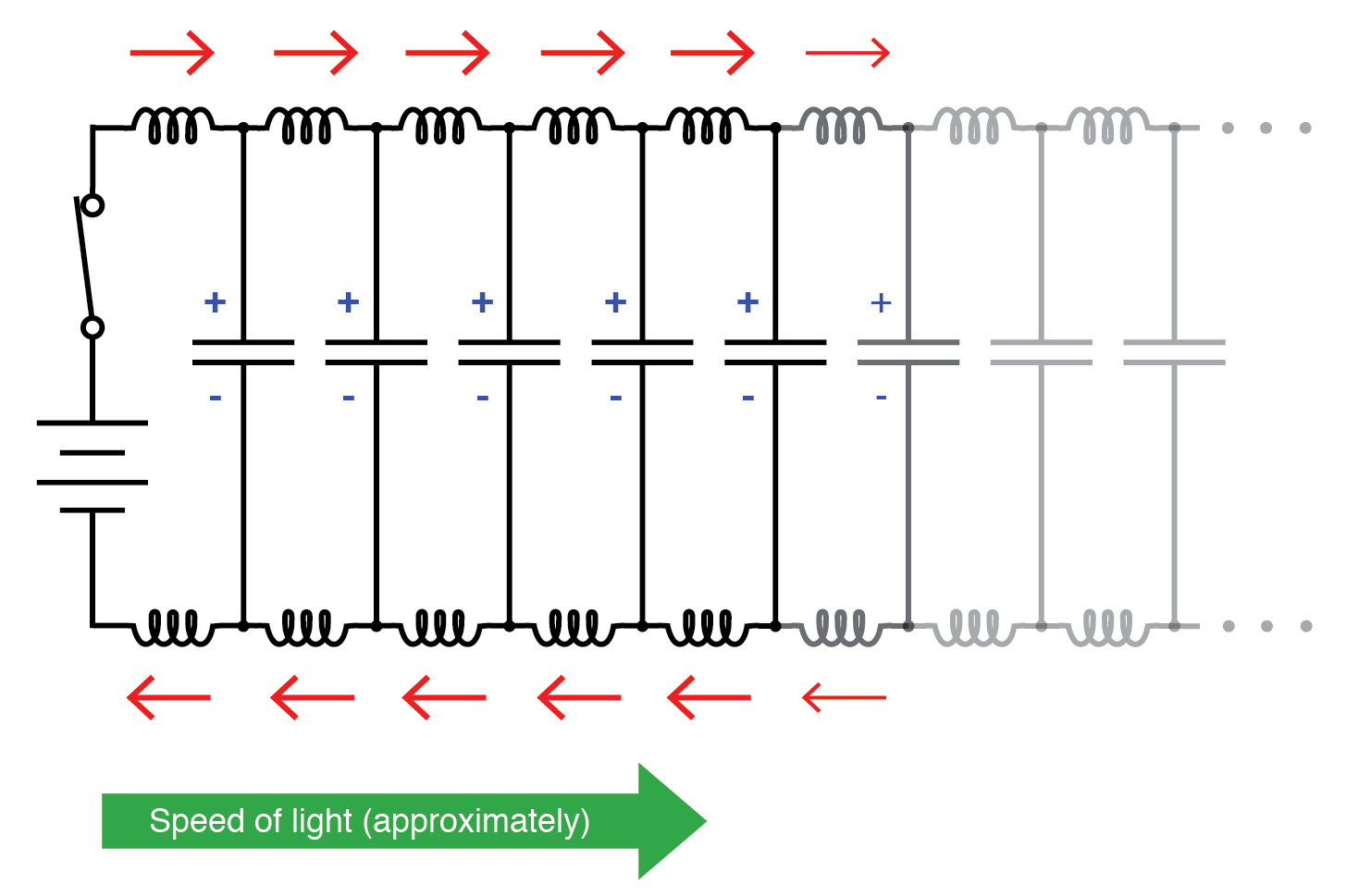
Propagar a la velocidad de la luz.

La línea de transmisión

El resultado final de estas interacciones es una corriente constante de magnitud limitada a través de la fuente de la batería. Dado que los cables son infinitamente largos, su capacitancia distribuida nunca se cargará completamente al voltaje de la fuente, y su inductancia distribuida nunca permitirá una corriente de carga ilimitada. En otras palabras, este par de cables extraerá corriente de la fuente siempre que el interruptor esté cerrado, comportándose como una carga constante. Los cables ya no son simplemente conductores de corriente eléctrica y portadores de voltaje, sino que ahora constituyen un componente de circuito en sí mismos, con características únicas. Los dos cables ya no son simplemente un par de conductores , sino más bien una línea de transmisión .

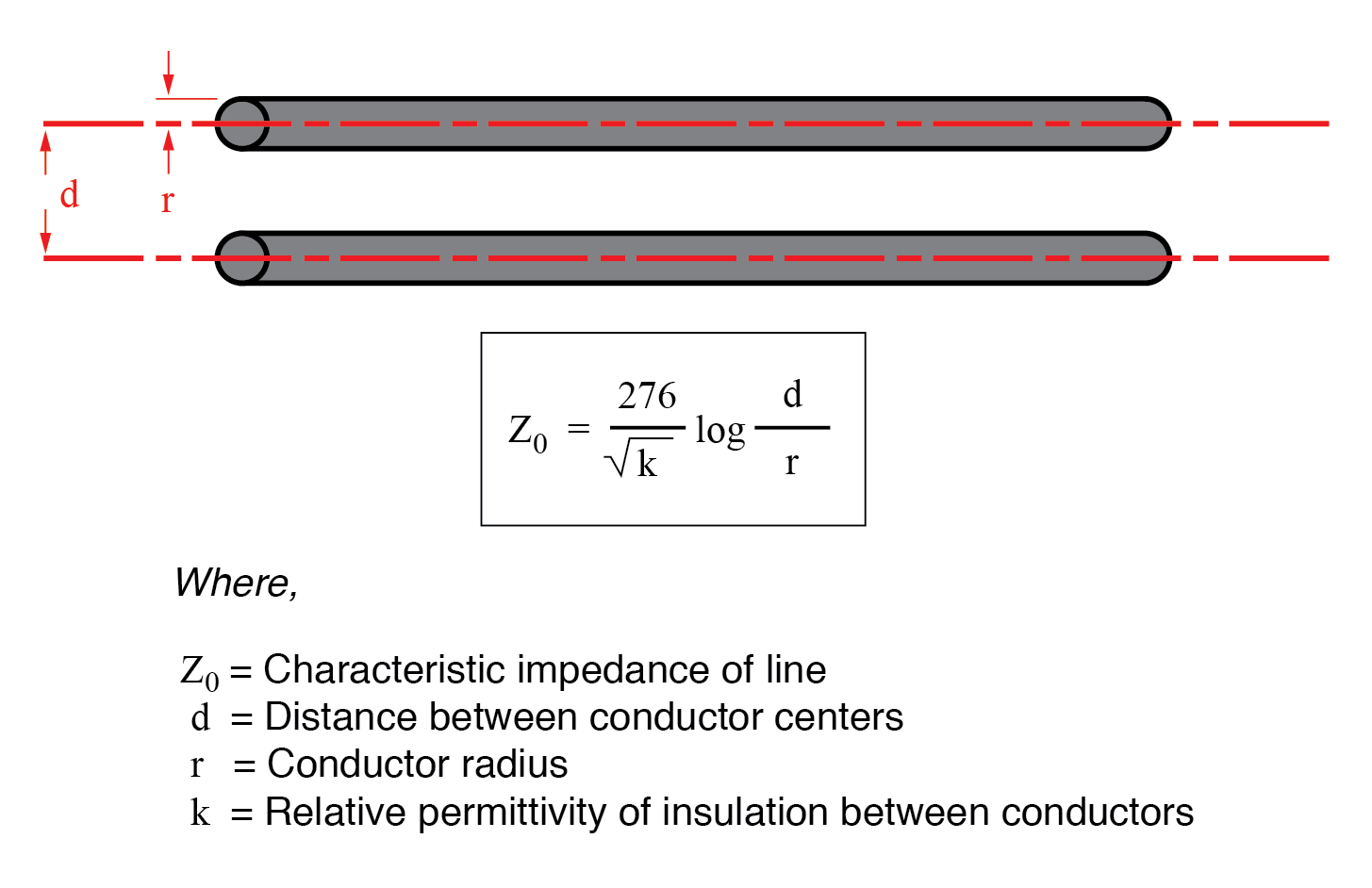
Como carga constante, la respuesta de la línea de transmisión al voltaje aplicado es resistiva en lugar de reactiva, a pesar de estar compuesta puramente por inductancia y capacitancia (asumiendo cables superconductores con resistencia cero). Podemos decir esto porque no hay diferencia desde la perspectiva de la batería entre una resistencia que disipa eternamente energía y una línea de transmisión infinita que absorbe energía eternamente. La impedancia (resistencia) de esta línea en ohmios se denomina impedancia característica , y está fijado por la geometría de los dos conductores. Para una línea de cables paralelos con aislamiento de aire, la impedancia característica se puede calcular como tal:

Si la línea de transmisión es de construcción coaxial, la impedancia característica sigue una ecuación diferente:

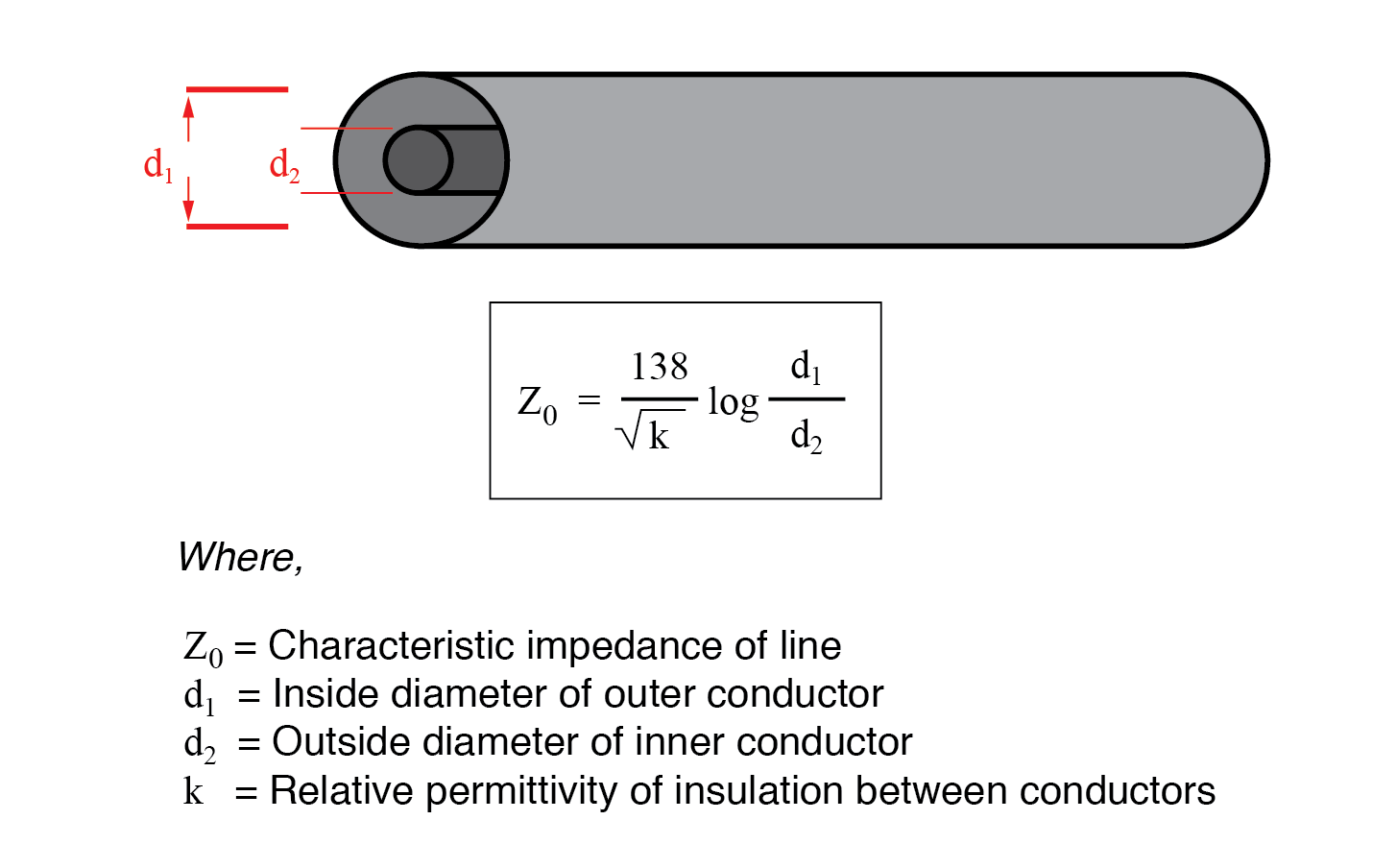
En ambas ecuaciones, se deben usar unidades de medida idénticas en ambos términos de la fracción. Si el material aislante no es aire (o vacío), tanto la impedancia característica como la velocidad de propagación se verán afectadas. La relación entre la velocidad de propagación real de una línea de transmisión y la velocidad de la luz en el vacío se denomina factor de velocidad de esa línea.

El factor de velocidad es simplemente un factor de la permitividad relativa del material aislante (también conocida como su constante dieléctrica ), definida como la relación entre la permitividad del campo eléctrico de un material y la de un vacío puro. El factor de velocidad de cualquier tipo de cable, coaxial o de otro tipo, se puede calcular de manera bastante simple mediante la siguiente fórmula:

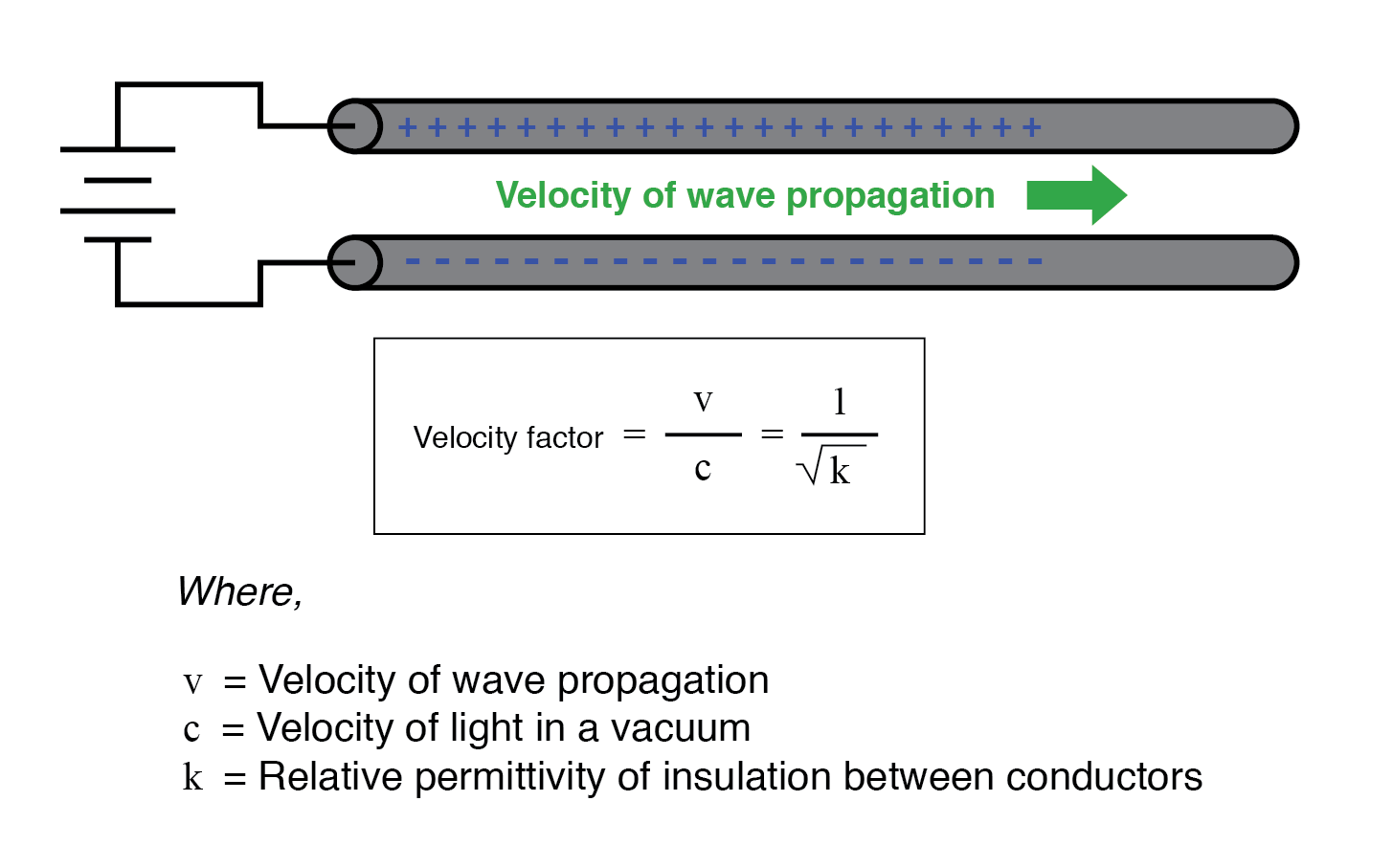
La impedancia natural

La impedancia característica también se conoce como impedancia natural , y se refiere a la resistencia equivalente de una línea de transmisión si fuera infinitamente larga, debido a la capacitancia e inductancia distribuidas a medida que las "ondas" de voltaje y corriente se propagan a lo largo de su longitud a una velocidad de propagación igual a una gran fracción de la velocidad de la luz.

Se puede ver en cualquiera de las dos primeras ecuaciones que la impedancia característica de una línea de transmisión (Z ₀ ) aumenta a medida que aumenta el espaciado de los conductores. Si los conductores se alejan entre sí, la capacitancia distribuida disminuirá (mayor espacio entre las “placas” del capacitor) y la inductancia distribuida aumentará (menos cancelación de los dos campos magnéticos opuestos). Menos capacitancia en paralelo y más inductancia en serie dan como resultado una menor corriente consumida por la línea para cualquier cantidad dada de voltaje aplicado, que por definición es una mayor impedancia. Por el contrario, acercar los dos conductores aumenta la capacitancia paralela y disminuye la inductancia en serie. Ambos cambios dan como resultado un consumo de corriente mayor para un voltaje aplicado dado, lo que equivale a una impedancia menor.

Salvo cualquier efecto disipativo, como la "fuga" dieléctrica y la resistencia del conductor, la impedancia característica de una línea de transmisión es igual a la raíz cuadrada de la relación de la inductancia de la línea por unidad de longitud dividida por la capacitancia de la línea por unidad de longitud:

REVISAR:

• Una línea de transmisión es un par de conductores paralelos que exhiben ciertas características debido a la capacitancia e inductancia distribuidas a lo largo de su longitud.
• Cuando un voltaje se aplica repentinamente a un extremo de una línea de transmisión, tanto una "onda" de voltaje como una "onda" de corriente se propagan a lo largo de la línea casi a la velocidad de la luz.
• Si se aplica un voltaje de CC a un extremo de una línea de transmisión infinitamente larga, la línea extraerá corriente de la fuente de CC como si fuera una resistencia constante.
• La impedancia característica (Z ₀ ) de una línea de transmisión es la resistencia que exhibiría si tuviera una longitud infinita. Esto es completamente diferente de la resistencia a las fugas del dieléctrico que separa los dos conductores y la resistencia metálica de los propios cables. La impedancia característica es puramente una función de la capacitancia y la inductancia distribuidas a lo largo de la línea y existiría incluso si el dieléctrico fuera perfecto (resistencia en paralelo infinita) y los cables superconductores (resistencia en serie cero).
• Factor de velocidad es un valor fraccionario relacionado con la velocidad de propagación de una línea de transmisión a la velocidad de la luz en el vacío. Los valores oscilan entre 0,66 y 0,80 para líneas típicas de dos hilos y cables coaxiales. Para cualquier tipo de cable, es igual al recíproco (1 / x) de la raíz cuadrada de la permitividad relativa del aislamiento del cable.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de impedancia característica