Divisor de voltaje

PIEZAS Y MATERIALES

• Calculadora (o lápiz y papel para hacer aritmética)
• batería de 6 voltios
• Surtido de resistencias entre 1 KΩ y 100 kΩ de valor

Estoy restringiendo deliberadamente los valores de resistencia entre 1 kΩ y 100 kΩ con el fin de obtener lecturas precisas de voltaje y corriente con su medidor.

Con valores de resistencia muy bajos, la resistencia interna del amperímetro tiene un impacto significativo en la precisión de la medición.

Los valores de resistencia muy altos pueden causar problemas para la medición de voltaje, la resistencia interna del voltímetro cambia sustancialmente la resistencia del circuito cuando se conecta en paralelo con una resistencia de alto valor.

REFERENCIAS CRUZADAS

Lecciones de circuitos eléctricos , Volumen 1, capítulo 6:"Circuitos divisores y leyes de Kirchhoff"

OBJETIVOS DE APRENDIZAJE

• Uso de voltímetro
• Uso de amperímetro
• Uso del ohmímetro
• Uso de la ley de Ohm
• Uso de la ley de voltaje de Kirchhoff ("KVL")
• Diseño de divisor de voltaje

DIAGRAMA ESQUEMÁTICO

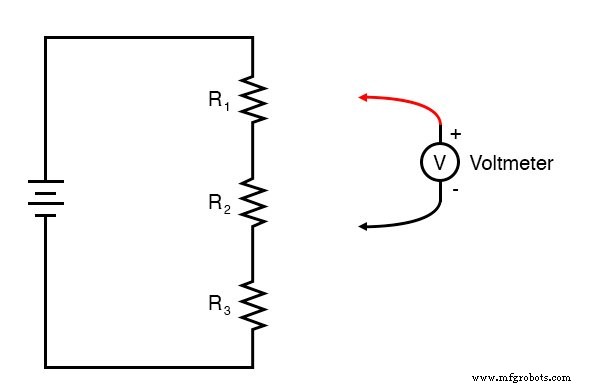
ILUSTRACIÓN

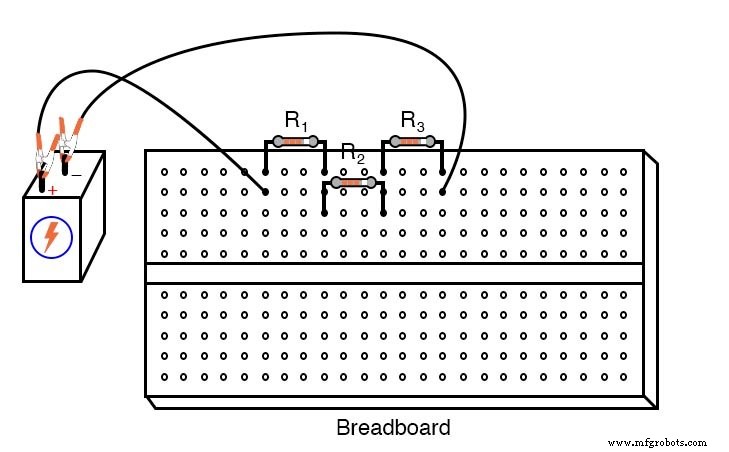
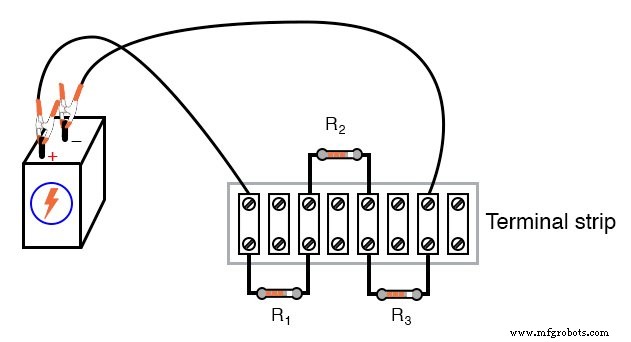
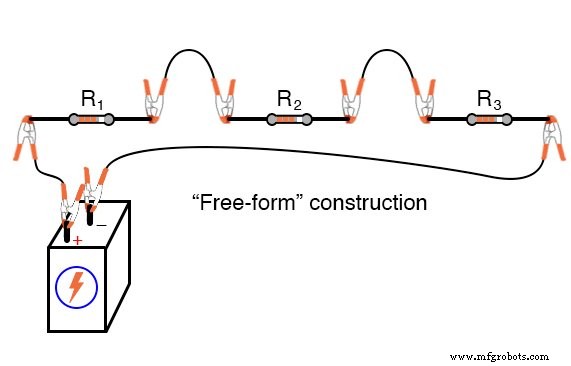
INSTRUCCIONES

Aquí se muestran tres métodos diferentes de construcción de circuitos:en una placa de pruebas, en una regleta de terminales y "forma libre".

Intente construir el mismo circuito en todos los sentidos para familiarizarse con las diferentes técnicas de construcción y sus respectivos méritos.

El método de "forma libre", en el que todos los componentes se conectan con cables de puente estilo "cocodrilo", es el menos profesional, pero apropiado para un experimento simple como este.

La construcción de la placa de pruebas es versátil y permite una alta densidad de componentes (muchas piezas en un espacio pequeño), pero es bastante temporal.

Las regletas de terminales ofrecen una forma de construcción mucho más permanente a costa de una baja densidad de componentes.

Seleccione tres resistencias de su variedad de resistencias y mida la resistencia de cada una con un ohmímetro.

Anote estos valores de resistencia con lápiz y papel, como referencia en los cálculos de su circuito.

Conecte las tres resistencias en serie y a la batería de 6 voltios, como se muestra en las ilustraciones.

Mida el voltaje de la batería con un voltímetro después de que se hayan conectado los resistores, y anote también esta cifra de voltaje en el papel.

Es recomendable medir el voltaje de la batería mientras se alimenta el circuito de resistencia porque este voltaje puede diferir ligeramente de una condición sin carga.

Vimos este efecto exagerado en el experimento de "batería paralela" mientras se enciende una lámpara de alto voltaje:el voltaje de la batería tiende a "hundirse" o "caer" bajo carga.

Aunque este circuito de tres resistencias no debe presentar una carga lo suficientemente pesada (no se consume suficiente corriente) para causar una “caída” de voltaje significativa, medir el voltaje de la batería bajo carga es una buena práctica científica porque proporciona datos más realistas.

Use la Ley de Ohm (I =E / R) para calcular la corriente del circuito, luego verifique este valor calculado midiendo la corriente con un amperímetro como este (la versión de "regleta de terminales" del circuito se muestra como una elección arbitraria en el método de construcción):

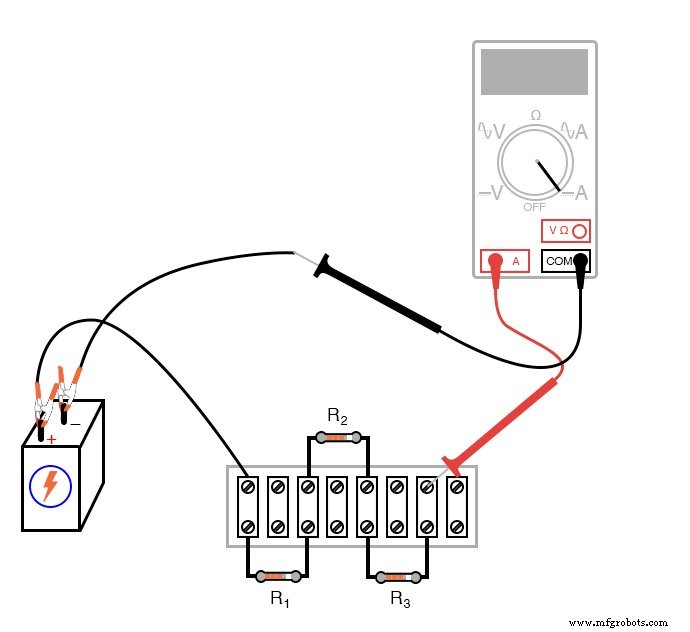
Si los valores de su resistencia están entre 1 kΩ y 100 kΩ, y el voltaje de la batería aproximadamente 6 voltios, la corriente debe ser un valor muy pequeño, en el rango de miliamperios (mA) o microamperios (µA).

Cuando mide corriente con un medidor digital, el medidor puede mostrar el símbolo de prefijo métrico apropiado (mo µ) en alguna esquina de la pantalla.

Estos indicadores de prefijos métricos son fáciles de pasar por alto al leer la pantalla de un medidor digital, ¡así que preste mucha atención!

El valor medido de la corriente debe coincidir estrechamente con el cálculo de la ley de Ohm.

Ahora, tome ese valor calculado para la corriente y multiplíquelo por las resistencias respectivas de cada resistor para predecir sus caídas de voltaje (E =IR).

Cambie su multímetro al modo de "voltaje" y mida el voltaje que cae en cada resistencia, verificando la precisión de sus predicciones.

Nuevamente, debe haber una estrecha concordancia entre las cifras de voltaje calculadas y medidas.

Cada caída de voltaje de la resistencia será una fracción o porcentaje del voltaje total, de ahí el nombre divisor de voltaje dado a este circuito.

Este valor fraccionario está determinado por la resistencia de la resistencia particular y la resistencia total.

Si una resistencia cae el 50% del voltaje total de la batería en un circuito divisor de voltaje, esa proporción del 50% seguirá siendo la misma siempre que los valores de la resistencia no se alteren.

Entonces, si el voltaje total es de 6 voltios, el voltaje a través de esa resistencia será 50% de 6 o 3 voltios. Si el voltaje total es de 20 voltios, esa resistencia caerá 10 voltios, o 50% de 20 voltios.

La siguiente parte de este experimento es una validación de la Ley de voltaje de Kirchhoff.

Para ello, debe identificar cada punto único del circuito con un número.

Los puntos que son eléctricamente comunes (conectados directamente entre sí con una resistencia insignificante entre ellos) deben llevar el mismo número.

Aquí se muestra un ejemplo que utiliza los números del 0 al 3 tanto en forma ilustrativa como esquemática.

En la ilustración, muestro cómo los puntos en el circuito se pueden etiquetar con pequeños trozos de cinta, números escritos en la cinta:

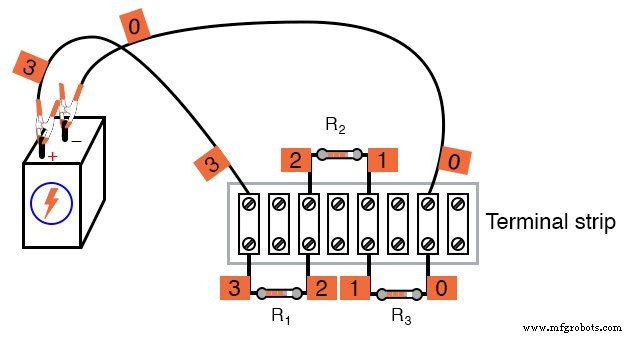
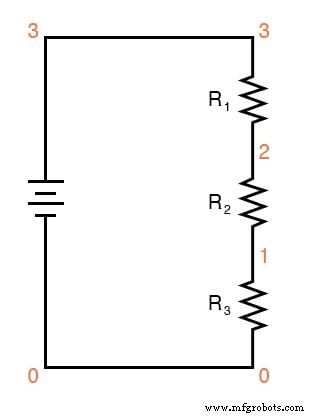
Usando un digital voltímetro (¡esto es importante!), mida las caídas de voltaje alrededor del lazo formado por los puntos 0-1-2-3-0.

Escriba en papel cada uno de estos voltajes, junto con su respectivo signo como lo indica el medidor.

En otras palabras, si el voltímetro registra un voltaje negativo como -1,325 voltios, debe escribir esa cifra como un número negativo.

No invierta las conexiones de la sonda del medidor con el circuito para que el número se lea "correctamente".

¡El signo matemático es muy significativo en esta fase del experimento! A continuación, se muestra una secuencia de ilustraciones que muestran cómo "rodear" el circuito, comenzando y terminando en el punto 0:

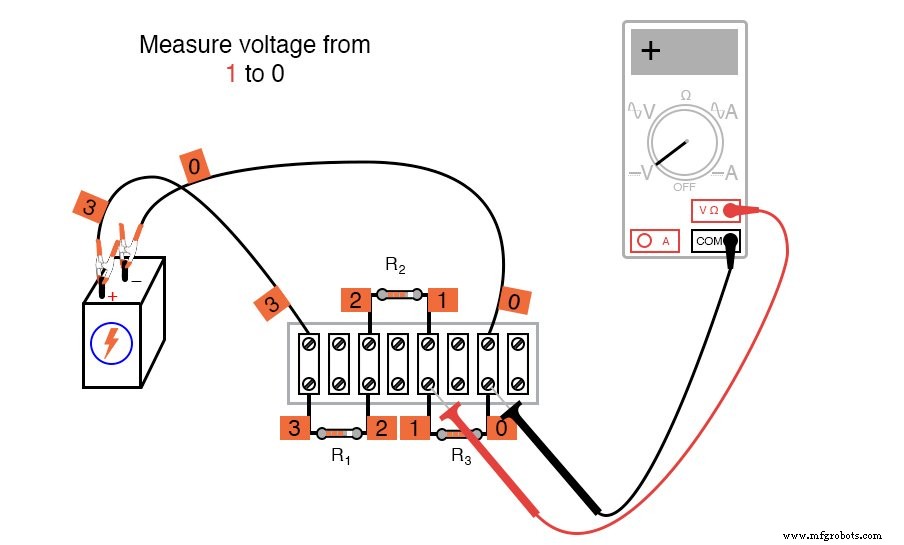
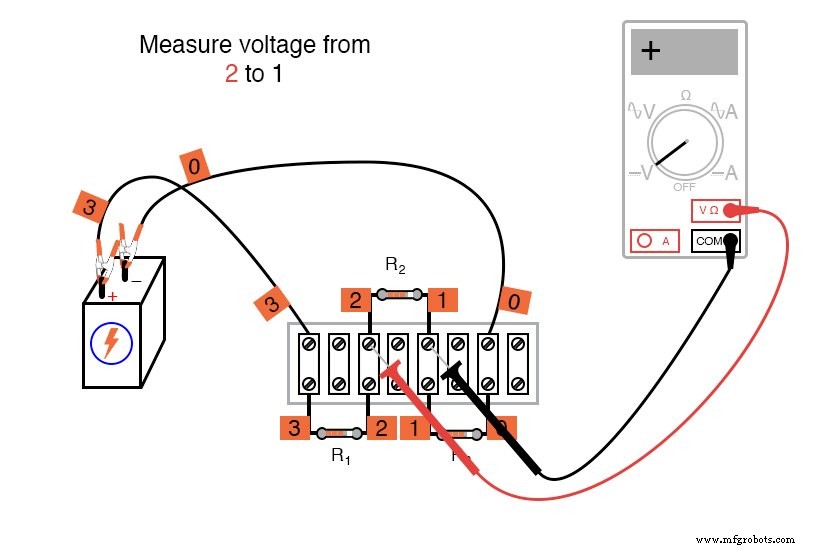
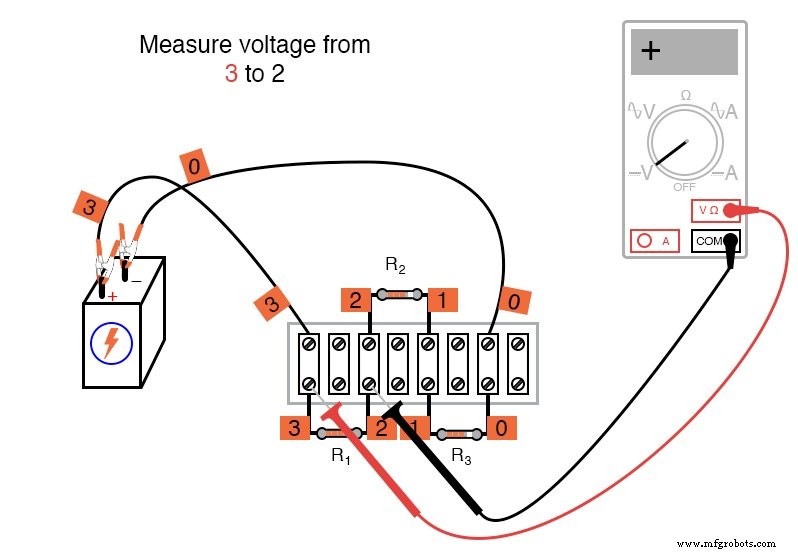
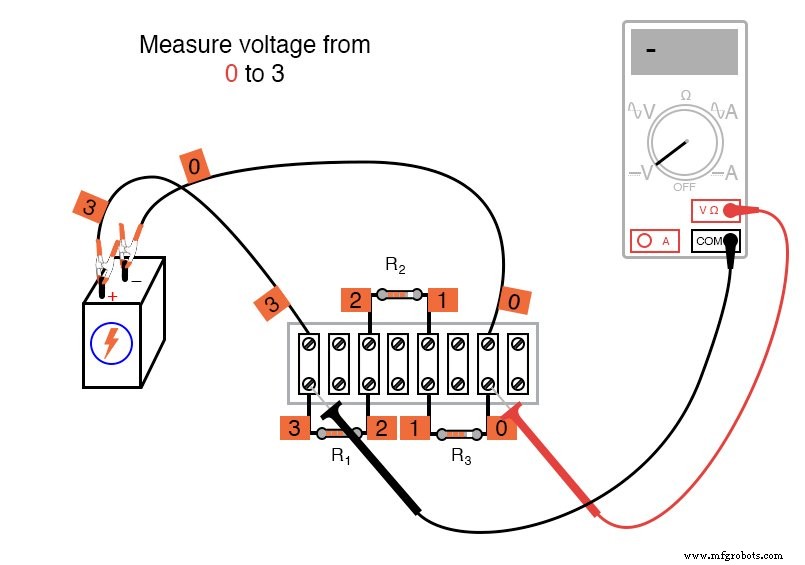
Usar el voltímetro para "dar un paso" alrededor del circuito de esta manera produce tres cifras de voltaje positivas y una negativa:

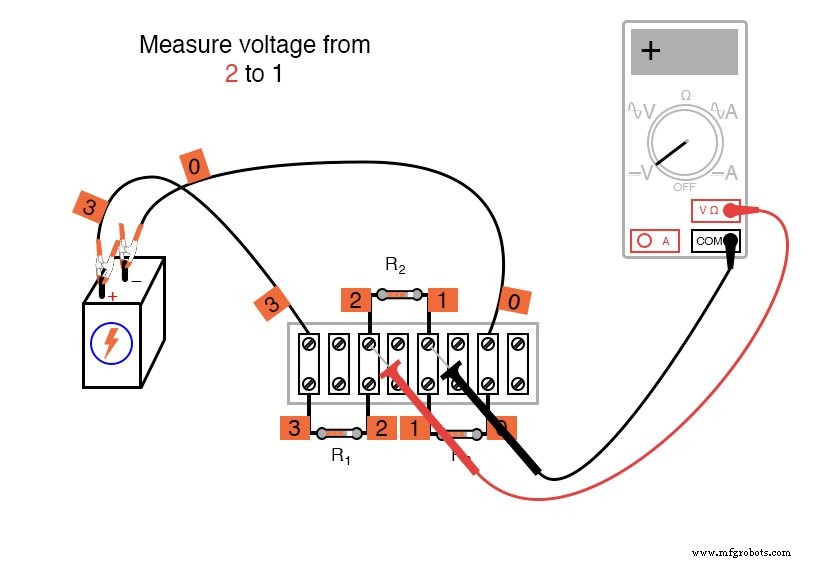
Estas cifras, sumadas algebraicamente ("algebraicamente" =respetando los signos de los números), deben ser iguales a cero.

Este es el principio fundamental de la ley del voltaje de Kirchhoff:que la suma algebraica de todas las caídas de voltaje en un "bucle" se suma a cero.

Es importante darse cuenta de que el "bucle" recorrido no tiene que ser el mismo camino que toma la corriente en el circuito, o incluso un camino de corriente legítimo en absoluto.

El bucle en el que contamos las caídas de voltaje puede ser cualquier conjunto de puntos , siempre que comience y termine con el mismo punto.

Por ejemplo, podemos medir y agregar los voltajes en el bucle 1-2-3-1, y también formarán una suma de cero:

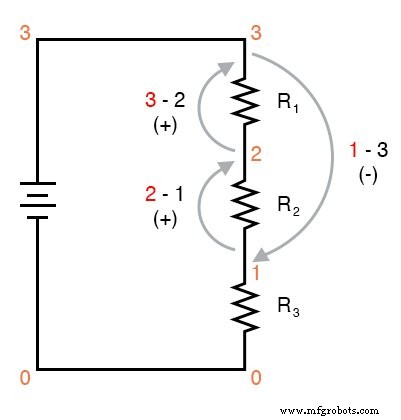
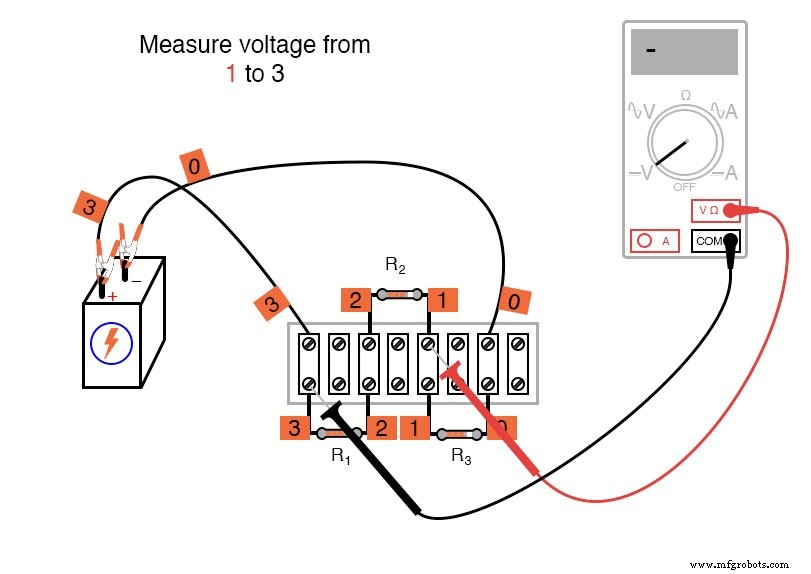
Intente caminar entre cualquier conjunto de puntos, en cualquier orden, alrededor de su circuito y compruebe por sí mismo que la suma algebraica siempre es igual a cero.

Esta ley es válida independientemente de la configuración del circuito:serie, paralelo, serie-paralelo o incluso una red irreducible.

La ley de voltaje de Kirchhoff es un concepto poderoso que nos permite predecir la magnitud y la polaridad de los voltajes en un circuito mediante el desarrollo de ecuaciones matemáticas para el análisis basadas en la verdad de todos los voltajes en un bucle que suman cero.

Este experimento tiene como objetivo proporcionar evidencia empírica y una comprensión profunda de la Ley de voltaje de Kirchhoff como principio general.

SIMULACIÓN DE COMPUTADORA

Netlist (haga un archivo de texto que contenga el siguiente texto, literalmente):

 Divisor de voltaje v1 3 0 r1 3 2 5k r2 2 1 3k r3 1 0 2k .dc v1 6 6 1 * Los voltajes alrededor del bucle 0-1-2-3-0 se suman algebraicamente a cero:.print dc v (1,0) v (2,1) v (3,2) v (0,3) * Los voltajes alrededor del ciclo 1-2-3-1 se suman algebraicamente a cero:.print dc v (2,1) v (3,2) v (1,3) .fin 

Esta simulación por computadora se basa en los números de puntos que se muestran en los diagramas anteriores para ilustrar la Ley de voltaje de Kirchhoff (puntos 0 a 3).

Los valores de resistencia se eligieron para proporcionar proporciones del 50%, 30% y 20% del voltaje total en R ₁ , R ₂ y R ₃ , respectivamente. Siéntase libre de modificar el valor de la fuente de voltaje (en el archivo " .dc ”, Que se muestra aquí como 6 voltios), y / o los valores de la resistencia.

Cuando se ejecuta, SPICE imprimirá una línea de texto que contiene cuatro cifras de voltaje, luego otra línea de texto que contiene tres cifras de voltaje, junto con muchas otras líneas de texto que describen el proceso de análisis. Sume las cifras de voltaje en cada línea para ver que la suma sea cero.

HOJAS DE TRABAJO RELACIONADAS:

Hoja de trabajo de circuitos divisores de voltaje