Revisión del teorema de Millman

Es posible que se haya preguntado de dónde obtuvimos esa extraña ecuación para la determinación del "Voltaje de Millman" en las ramas paralelas de un circuito donde cada rama contiene una resistencia en serie y una fuente de voltaje:

Partes de esta ecuación parecen familiares para las ecuaciones que hemos visto antes. Por ejemplo, el denominador de la fracción grande se parece notablemente al denominador de nuestra ecuación de resistencia paralela. Y, por supuesto, los términos E / R en el numerador de la fracción grande deberían dar cifras para la corriente, siendo la ley de Ohm la que es (I =E / R).

Ahora que hemos cubierto las equivalencias de fuentes de Thevenin y Norton, tenemos las herramientas necesarias para comprender la ecuación de Millman. Lo que realmente hace la ecuación de Millman es tratar cada rama (con su fuente de voltaje en serie y su resistencia) como un circuito equivalente de Thevenin y luego convertir cada una en circuitos Norton equivalentes.

Circuito equivalente de Thevenin

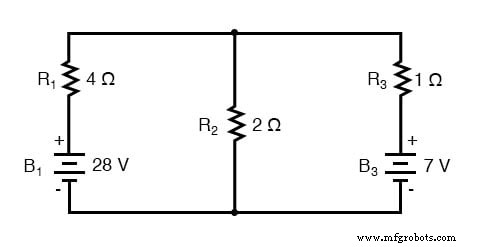
Por lo tanto, en el circuito anterior, la batería B1 y la resistencia R1 se ven como una fuente de Thevenin que se convertirá en una fuente Norton de 7 amperios (28 voltios / 4 Ω) en paralelo con una resistencia de 4 Ω. La rama más a la derecha se convertirá en una fuente de corriente de 7 amperios (7 voltios / 1 Ω) y una resistencia de 1 Ω en paralelo. La rama central, que no contiene ninguna fuente de voltaje, se convertirá en una fuente Norton de 0 amperios en paralelo con una resistencia de 2 Ω:

Circuito equivalente de Norton

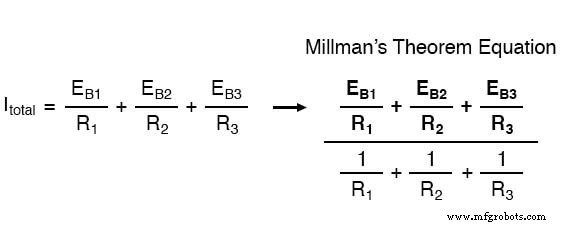
Dado que las fuentes de corriente agregan directamente sus respectivas corrientes en paralelo, la corriente total del circuito será 7 + 0 + 7, o 14 amperios. Esta adición de las corrientes de origen de Norton es lo que se representa en el numerador de la ecuación de Millman:

Ecuación de Millman

Todas las resistencias Norton están en paralelo entre sí también en el circuito equivalente, por lo que disminuyen para crear una resistencia total. Esta disminución de las resistencias de la fuente es lo que se representa en el denominador de la ecuación de Millman:

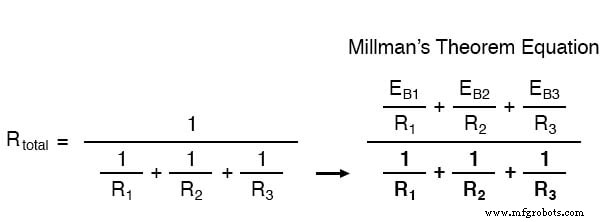
En este caso, la resistencia total será igual a 571,43 miliohms (571,43 mΩ). Podemos volver a dibujar nuestro circuito equivalente ahora como uno con una sola fuente de corriente Norton y resistencia Norton:

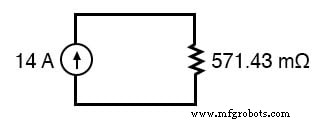
La ley de Ohm puede decirnos el voltaje a través de estos dos componentes ahora (E =IR):

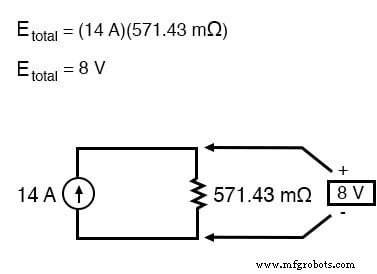
Resumamos lo que sabemos sobre el circuito hasta ahora. Sabemos que la corriente total en este circuito está dada por la suma de todos los voltajes de rama dividida por sus respectivas resistencias. También sabemos que la resistencia total se encuentra tomando el recíproco de todos los recíprocos de resistencia de las ramas. Además, debemos ser conscientes del hecho de que el voltaje total en todas las ramas se puede encontrar multiplicando la corriente total por la resistencia total (E =IR). Todo lo que tenemos que hacer es juntar las dos ecuaciones que teníamos anteriormente para la corriente total del circuito y la resistencia total, multiplicándolas para encontrar el voltaje total:

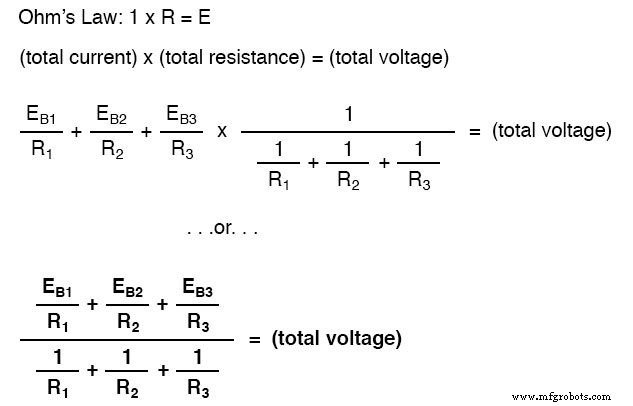
La ecuación de Millman no es más que una conversión de Thevenin a Norton combinada con la fórmula de resistencia en paralelo para encontrar el voltaje total en todas las ramas del circuito. ¡Entonces, con suerte, parte del misterio se ha ido ahora!

HOJA DE TRABAJO RELACIONADA:

• Hoja de trabajo del teorema de Millman