19 Unidad 2:Ejes programables de máquina herramienta CNC y sistemas de acotación de posición
OBJETIVO
Después de completar esta unidad, debería poder:
- Comprender el sistema de coordenadas cartesianas.
- Comprender las coordenadas cartesianas del plano.
- Comprender las coordenadas cartesianas del espacio tridimensional.
- Comprender los cuatro cuadrantes.
- Explica la diferencia entre coordenadas polares y rectangulares.
- Identificar los ejes programables en un mecanizado CNC.
EL SISTEMA DE COORDENADAS CARTESIANAS
Las coordenadas cartesianas permiten especificar la ubicación de un punto en el plano o en el espacio tridimensional. Las coordenadas cartesianas o el sistema de coordenadas rectangulares de un punto son un par de números (en dos dimensiones) o un triplete de números (en tres dimensiones) que especifican distancias con signo desde el eje de coordenadas. Primero debemos entender un sistema de coordenadas para definir nuestras direcciones y posición relativa. Sistema utilizado para definir puntos en el espacio estableciendo direcciones (eje) y una posición de referencia (origen). Un sistema de coordenadas puede ser rectangular o polar.
Así como los puntos en la línea se pueden colocar en correspondencia uno a uno con la línea de números reales, los puntos en el plano se pueden colocar en correspondencia uno a uno con pares de líneas de números reales usando dos líneas de coordenadas. Para hacer esto, construimos dos líneas de coordenadas perpendiculares que se cortan en sus orígenes; por conveniencia. Asigne un conjunto de graduaciones de espacios iguales a los ejes x e y comenzando en el origen y yendo en ambas direcciones, izquierda y derecha (eje x) y arriba y abajo (eje y) se puede establecer un punto a lo largo de cada eje. Hacemos que una de las rectas numéricas sea vertical con su dirección positiva hacia arriba y su dirección negativa hacia abajo. Las otras rectas numéricas son horizontales con su dirección positiva a la derecha y su dirección negativa a la izquierda. Las dos rectas numéricas se llaman ejes de coordenadas; la línea horizontal es el eje x, la línea vertical es el eje y, y los ejes de coordenadas juntos forman el sistema de coordenadas cartesianas o un sistema de coordenadas rectangulares. El punto de intersección de los ejes de coordenadas se denota por O y es el origen del sistema de coordenadas. Consulte la figura 1.
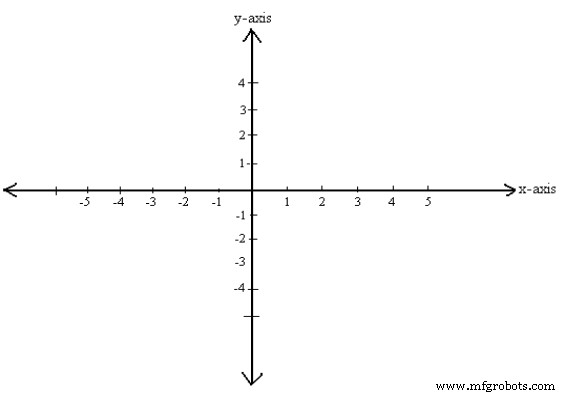
Figura 1
Es básicamente, dos rectas numéricas reales juntas, una de izquierda a derecha y la otra de arriba a abajo. La línea horizontal se llama eje x y la línea vertical se llama eje y.
El Origen
Al punto (0,0) se le da el nombre especial "El origen" y, a veces, se le da la letra "O".
Recta de números reales
La base de este sistema es la recta numérica real marcada a intervalos iguales. El eje está etiquetado (X, Y o Z). Un punto en la línea se designa como el Origen. Los números de un lado de la línea se marcan como positivos y los del otro lado se marcan como negativos. Consulte la figura 2.
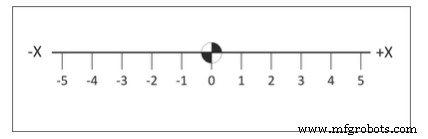
Figura 2. Recta numérica del eje X
Coordenadas cartesianas del plano
Un plano en el que se ha introducido un sistema de coordenadas rectangulares es un plano de coordenadas o un plano x-y. Ahora mostraremos cómo establecer una correspondencia uno a uno entre puntos en un plano de coordenadas y pares de números reales. Si A es un punto en un plano de coordenadas, entonces dibujamos dos líneas a través de A, una perpendicular al eje x y otra perpendicular al eje y. Si la primera línea se cruza con el eje x en el punto con la coordenada x y la segunda línea se cruza con el eje y en el punto con la coordenada y, entonces asociamos el par (x, y) con la A (consulte la figura 2). El número a es la coordenada x o abscisa de P y el número b es la coordenada y u ordenada de p; decimos que A es el punto con coordenadas (x,y) y denotamos el punto por A(x,y). Al punto (0,0) se le da el nombre especial "El origen" y, a veces, se le da la letra "O".
Abscisa y ordenada:
Las palabras "Abscisa" y "Ordinada"... son solo los valores de xandy:
- Abscisa:el valor horizontal ("x") en un par de coordenadas:qué tan lejos está el punto.
- Ordenada:el valor vertical ("y") en un par de coordenadas:qué tan arriba o abajo está el punto.
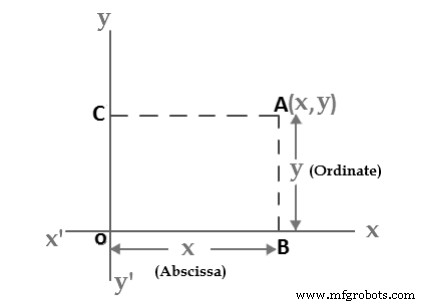
Figura 3
Valores negativos de X e Y:
La recta numérica real, también puede tener valores negativos.
Negativo:comienza en cero y dirígete en la dirección opuesta; Ver Figura 4
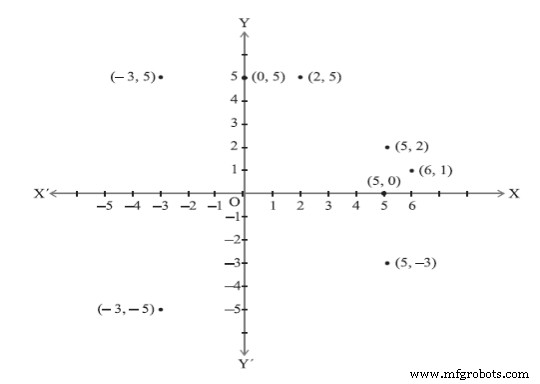
Figura 4
Entonces, para un número negativo:
- ir a la izquierda por x
- godownfor y
ir a la izquierda a lo largo del eje x 3 y luego subir 5 en el eje y. (El cuadrante II x es negativo, y es positivo) Y (-3,-5) significa:
ir hacia la izquierda a lo largo del eje x 3 y luego ir hacia abajo 5 en el eje y. (El cuadrante III x es negativo,y es negativo)Usando coordenadas cartesianas, marque un punto en un gráfico por qué tan lejos y qué tan arriba está; Vea la figura 5. El punto (12,5) está 12 unidades a lo largo del eje x y 5 unidades arriba en el eje y.
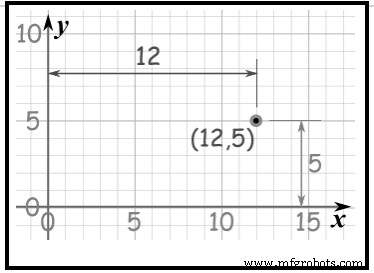 Figura 5Ejes X e Y:
Figura 5Ejes X e Y: 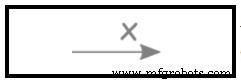 La línea horizontal se llama eje x y la línea vertical se llama eje y; ambas líneas pasan por cero (Origen, (0,0)).
La línea horizontal se llama eje x y la línea vertical se llama eje y; ambas líneas pasan por cero (Origen, (0,0)).  La línea horizontal se llama eje x y la línea vertical se llama eje y; ambas líneas pasan por cero (Origen, (0,0)). Póngalos juntos en un gráfico... Vea la figura 6
La línea horizontal se llama eje x y la línea vertical se llama eje y; ambas líneas pasan por cero (Origen, (0,0)). Póngalos juntos en un gráfico... Vea la figura 6 
Figura 6
Es básicamente, un conjunto de dos líneas de números reales.
Eje:La línea de referencia a partir de la cual se miden las distancias.
Ejemplo:
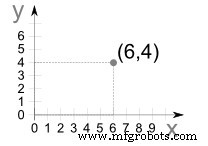 El punto (6,4) es
El punto (6,4) es Vaya a lo largo de la dirección x 6 unidades, luego suba 4 unidades en la dirección y luego "trace el punto".
Y puede recordar qué eje es cuál por:
Las coordenadas siempre se escriben en un orden determinado:
- la distancia horizontal primero,
- luego la distancia vertical.
Par ordenado:
Los números están separados por una coma y los paréntesis se colocan alrededor de todo de la siguiente manera: (7,4)
Ejemplo:(7,4) significa 7 unidades a la derecha (eje x) y 4 unidades hacia arriba (eje y)
Coordenadas cartesianas del espacio tridimensional
En el espacio tridimensional (espacio xyz), orientado en ángulo recto con el plano xy. El eje z pasa por el origen del plano xy. Las coordenadas se determinan de acuerdo con los desplazamientos desde el origen de este a oeste para el eje x, de norte a sur para el eje y, y de arriba a abajo para el eje z. El sistema de coordenadas cartesianas se basa en tres ejes de coordenadas perpendiculares entre sí:el eje x, el eje y y el eje z. Consulte la Figura 6 a continuación. Los tres ejes se cortan en el punto llamado origen. Puede imaginar que el origen es el punto donde las paredes en la esquina de una habitación se encuentran con el piso. El eje x es la línea horizontal a lo largo de la cual se cruzan la pared a su izquierda y el piso. El eje-y es la línea horizontal a lo largo de la cual se cruzan la pared a su derecha y el piso. El eje z es la línea vertical a lo largo de la cual se cruzan las paredes. Las partes de las líneas que ves mientras estás parado en la habitación son la parte positiva de cada uno de los ejes. La parte negativa de estos ejes serían las continuaciones de las líneas fuera de la habitación.
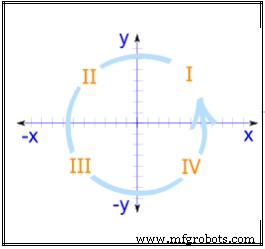
Figura 7. Sistema de coordenadas cartesianas 3D
Ejes de coordenadas cartesianas tridimensionales. Una representación de los tres ejes del sistema de coordenadas cartesiano tridimensional. El eje x positivo, el eje y positivo y el eje z positivo son los lados etiquetados por x, yyz. El origen es la intersección de todos los ejes. La rama de cada eje en el lado opuesto del origen (el lado sin etiquetar) es la parte negativa.
Cuando se trata de movimiento tridimensional, es establecer un sistema de coordenadas adecuado. El tipo de sistema de coordenadas más sencillo se llama sistema cartesiano. Un sistema de coordenadas cartesianas consta de tres ejes mutuamente perpendiculares, los ejes X, Y y Z. Por convención, la orientación de estos ejes es tal que cuando el dedo índice, el dedo medio y el pulgar de la mano derecha están configurados para ser mutuamente perpendiculares, el dedo índice, el dedo medio y el pulgar pueden ser alineados a lo largo de los ejes X, Y y Z, respectivamente. Tal sistema de coordenadas se denomina diestro. Consulte la Figura 7. El punto de intersección de los tres ejes de coordenadas se denomina el origen del sistema de coordenadas.
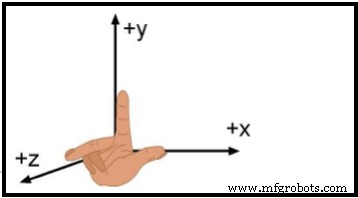
Figura 8. El sistema cartesiano de mano derecha
Las coordenadas cartesianas de un punto en tres dimensiones son un triplete de números (x,y,z). Los tres números, o coordenadas, especifican la distancia con signo desde el origen a lo largo de los ejes x, y y z, respectivamente. Se pueden visualizar formando el cuadro con bordes paralelos al eje de coordenadas y esquinas opuestas en el origen y el punto dado.
Los puntos ahora pueden definirse en un volumen de espacio tridimensional. Esto permite definir puntos en tres dimensiones desde el origen. Las coordenadas cartesianas (x, y, z) de un punto en tres dimensiones especifican la distancia con signo desde el origen a lo largo de los ejes x, y y z, respectivamente. Los puntos del eje Z se convierten en la tercera entrada al definir ubicaciones de coordenadas.
Dada la analogía anterior de la esquina de la habitación, podríamos formar las coordenadas cartesianas del punto en la parte superior de su cabeza, de la siguiente manera. Imagina que tienes cinco metros de altura en el eje z y que caminas dos metros desde el origen a lo largo del eje x, luego giras a la izquierda y caminas en paralelo al eje y cuatro metros dentro de la habitación. Las coordenadas cartesianas del punto en la parte superior de tu cabeza serían (2,4,5).
Por ejemplo, una notación de (2,4,5) corresponde al valor de X2, Y4 y Z5. Consulte la figura 8.
3 Dimensiones
Las coordenadas cartesianas se pueden usar para ubicar puntos en 3 dimensiones como en este ejemplo:

Figura 9. El punto (2, 4, 5 ) se muestra en coordenadas cartesianas tridimensionales.
Cuadrantes
Los ejes de coordenadas dividen el plano en cuatro partes, llamadas cuadrantes (Ver Figura 9). Los cuadrantes se numeran en sentido antihorario, comenzando desde la parte superior derecha, etiquetados como I, II, III y IV con designaciones de ejes como se muestra en la siguiente ilustración.
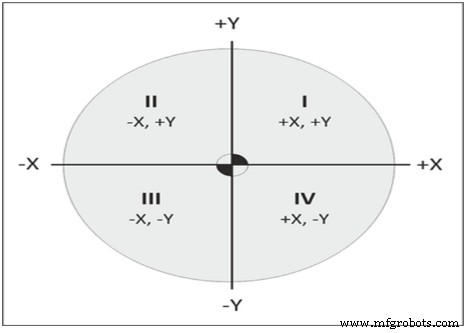
Figura 10
Cuatro Cuadrantes:
Cuando incluimos valores negativos, los ejes x e y dividen el espacio en 4 partes:
Cuadrantes I, II, III y IV
(Están numerados en sentido contrario a las agujas del reloj)

En el Cuadrante I:tanto x como y son positivos
InQuadrant II:x es negativo (y sigue siendo positivo)
En el Cuadrante III:tanto x como y son negativos
InQuadrant IV :x vuelve a ser positivo, mientras que y es negativo
| Cuadrante | X (Horizontal) | Y (Vertical) | Ejemplo |
| Yo | Positivo | Positivo | (3,2) |
| II | Negativo | Positivo | (-5, 2) |
| III | Negativo | Negativo | (-2, -1) |
| IV | Positivo | Negativo | (2, -5) |
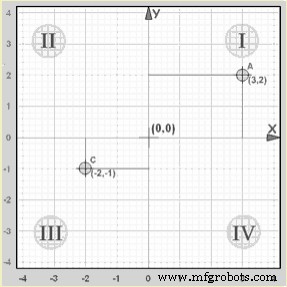
Ejemplo:El punto "A" (3,2) está 3 unidades a lo largo del eje x y 2 unidades arriba del eje y.
Tanto x como y son positivos, por lo que ese punto está en el "Cuadrante I"
Ejemplo:El punto "C" (-2,-1) está 2 unidades a lo largo del eje x en dirección negativa y 1 unidad hacia abajo en el eje y en dirección negativa.
Tanto x como y son negativos, por lo que ese punto está en el “Cuadrante III”
Dimensiones:1, 2, 3 y más…
1. La recta numérica real solo puede ir:
- izquierda-derecha
- por lo que cualquier posición necesita solo un número
2. Las coordenadas cartesianas pueden ir:
- izquierda-derecha, y
- arriba-abajo
- por lo que cualquier puesto necesita dos números
3. 3 dimensiones
- izquierda-derecha,
- arriba-abajo, y
- adelante-atrás
PRUEBA DE UNIDAD
1. ¿Qué es CNC?
2. Describa el sistema de coordenadas cartesianas.
3. ¿Qué es El Origen?
4. ¿Cómo se llama la línea horizontal?
5. ¿Cómo se llama la línea vertical?
6. Describe la recta numérica real.
7. Explique las abscisas y las ordenadas.
8. ¿Cuáles son la representación de los tres ejes del sistema de coordenadas cartesianas tridimensional?
9. Los ejes de coordenadas dividen el plano en cuatro partes, ¿cómo se llama?
10. En el Cuadrante IV, ¿cuáles son los ejes X y los ejes Y?
Tecnología Industrial
- Máquina herramienta CNC
- ¿Cómo utilizar una fresadora CNC?
- Cómo mejorar la precisión de las máquinas herramienta CNC
- Operaciones de máquinas de torno y herramientas de corte de torno
- ¿Qué es la máquina cepilladora? Definición, partes y tipos
- Cómo la IA y el aprendizaje automático impactan en el mecanizado CNC
- Protección contra incendios de máquinas EDM y CNC:comparación de sus opciones
- 22 Unidad 5:Operación CNC
- Maximización de la precisión y el posicionamiento de las máquinas herramienta CNC
- Partes y elementos de sistemas de máquinas CNC
- Códigos G y códigos M de máquina CNC:fresado y torno CNC



