Polarización de valle controlable mediante defectos de línea doble de silicene debido al acoplamiento Rashba Spin-Orbit
Resumen
Teóricamente investigamos la polarización del valle en silicene con dos defectos de línea paralela debido al acoplamiento de órbita-espín de Rashba (RSOC). Se encuentra que mientras RSOC excede el acoplamiento intrínseco espín-órbita (SOC), los coeficientes de transmisión de los dos valles oscilan con la misma periodicidad e intensidad, que consiste en picos de transmisión amplios y mesetas de transmisión cero. Sin embargo, en presencia de un campo eléctrico perpendicular, la periodicidad de oscilación del primer valle aumenta, mientras que la del segundo valle se acorta, generando las correspondientes regiones de meseta amplia de pico cero, donde se puede lograr una polarización de valle perfecta. Además, la polarización del valle se puede cambiar de 1 a -1 controlando la fuerza del campo eléctrico. Nuestros hallazgos establecen una ruta diferente para generar corriente polarizada en valle por medios puramente eléctricos y abren la puerta a aplicaciones interesantes de los Valleytronics de semiconductores.
Introducción
El silicene, una red de átomos de silicio en forma de panal de abeja de bajo pandeo, es una alternativa potencialmente atractiva al grafeno para aplicaciones valleytronic. La estructura de pandeo bajo da lugar a un acoplamiento de órbita-espín (SOC) relativamente grande en silicene, y se estima una brecha de energía considerable de aproximadamente 1,55 meV en los puntos de Dirac K y K ′ [1] A diferencia del grafeno, la relación de dispersión de baja energía del silicio es parabólica en lugar de lineal. Facilitada por la estructura de pandeo, la estructura de banda del silicene puede controlarse aplicando un campo eléctrico, e incluso puede ocurrir una transición de fase topológica de un aislador Hall de espín cuántico a un aislador de Hall Valley cuántico [2, 3]. El silicene se ha sintetizado con éxito en la superficie de sustratos como Ag (111), Ir (111) y ZrB2 (0001) [4-6], y su estructura estable independiente también se ha predicho en varios estudios teóricos [7 ]. Lo que es más importante, un transistor de efecto de campo (FET) de silicio a temperatura ambiente se ha observado con éxito de forma experimental [8]. La sintonización del campo eléctrico y la compatibilidad con los dispositivos existentes basados en silicio hacen que el silicio sea un material bidimensional potencial para su aplicación en los Valleytronics de próxima generación.
En materiales bidimensionales (2D) como el grafeno y dicalcogenuros de metales de transición (MoS 2 , etc.), los límites de grano entre dos dominios de material con diferentes orientaciones cristalográficas son opciones ideales para lograr la polarización del valle y han atraído una atención considerable [9-14]. Recientemente, los defectos de línea extendida (ELD) en silicene se han investigado extensamente de acuerdo con los cálculos de los primeros principios [15, 16], y se encontró que el ELD 5-5-8 (abreviado como "defecto de línea" a continuación) es la estructura más estable y más fácil de formar. La polarización de espín y valle del defecto de la línea de silicene se ha investigado teóricamente [17-19]. La formación de un defecto de línea se puede visualizar como la costura de los bordes en zigzag de dos granos de Si por los átomos de Si adsorbidos, donde cualquiera de los lados del defecto de línea muestra un comportamiento similar al de un pseudoborde y los límites de grano del borde en zigzag actúan como el pseudoborde [16]. Obviamente, tal celosía tiene simetría especular con respecto a la línea defecto y los vectores reticulares correspondientes en los dominios "izquierdo" y "derecho" separados por el defecto son contrarios [10, 11]. En tal defecto de línea con límite de dominio de inversión, el A / B las subredes y los índices de valle se intercambian al cruzar el defecto. El defecto de línea es semitransparente para las cuasipartículas en grafeno y aparece una polarización de alto valle con un alto ángulo de incidencia. La polarización del valle es q y (la velocidad del grupo de electrones a lo largo de y dirección) dependiente a través del defecto de línea. Para el grafeno, que tiene una dispersión lineal y una velocidad de grupo constante, la polarización del valle puede alcanzar cerca del 100% en general | q y | (correspondiente a un alto ángulo de incidencia) mientras que disminuye a medida que | q y | disminuye y desaparece como | q y | ∼0 [9, 14]. Por el contrario, el silicene tiene dos características de transmisión diferentes [17, 18]:en primer lugar, los dos valles se vuelven indistinguibles a medida que la energía de Fermi está cerca del borde de la banda debido a la relación de dispersión parabólica, y en segundo lugar, la transmisión está restringida debido a la hélice el estado de borde fluye inversamente a ambos lados del defecto de línea, como se muestra en la Fig. 1c. Naturalmente, el sistema con SOC en un RSOC en particular es un candidato prometedor para un FET de giro eficiente. El RSOC genera un campo magnético efectivo en el plano e induce la precesión de espín que se inyecta perpendicular al plano de confinamiento. La polarización de espín [20] y la inversión [21] se han investigado en nanocintas de siliceno controladas. Los cálculos teóricos han demostrado que la banda de energía del silicene puede ser modulada significativamente por RSOC [22, 23]. Por ejemplo, en un RSOC relativamente fuerte, la banda de descenso (-up) en el K ( K ′ ) el valle se desplaza hacia arriba mientras que las otras bandas de giro en la banda de conducción permanecen sin cambios. Teniendo en cuenta la característica de transmisión peculiar en el defecto de la línea de silicene y el efecto de RSOC en silicene, los esquemas prácticos totalmente eléctricos para generar portadoras polarizadas en valle se vuelven factibles.
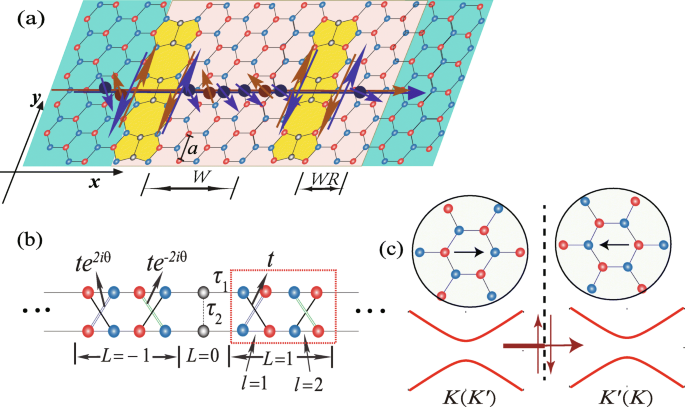
un Diagrama esquemático del proceso de precesión de los estados ( K , ↑ ) (esfera roja) y ( K ′ , ↓ ) (esfera azul) a través de una lámina de silicona con dos defectos de líneas paralelas, donde el círculo azul (rojo) denota la A ( B ) subred. Los estados ( K , ↑ ) y ( K ′ , ↓ ) circulan a lo largo del pseudoborde, y se supone que el RSOC y el campo eléctrico existen en la región gris francesa. W ( W =2) y WR ( WR =1) representan el ancho de la región de dispersión en unidades de \ (\ sqrt {3} a \). b El modelo de celosía simplificado del siliceno infinito con un defecto de línea, donde θ = k y a y el rectángulo punteado corresponde a una supercélula. En la celda unitaria, los puntos de la red se especifican mediante un conjunto de índices ( L, l ). c La transmisión para un estado de giro en K ( K ′ ) valle a través del defecto de línea con límites de dominio de inversión. Los recuadros muestran la orientación de la red cristalina en los dos dominios separados por el defecto de línea (línea discontinua). Las líneas gruesas / finas indican que la transmisión está restringida a través del defecto de línea debido a que los estados del borde helicoidal fluyen inversamente a lo largo del pseudoborde
En este artículo, proponemos una forma eficiente de polarizar los fermiones de Dirac de diferentes valles utilizando los defectos de doble línea de silicio, creando así una polarización de valle distinta mediante la utilización del campo eléctrico en el silicio. Nuestros resultados muestran que cuando la energía de Fermi está cerca de la parte inferior de la banda de conducción, las imágenes de oscilación de los coeficientes de transmisión de dos valles, que comprenden picos oscilantes anchos y nadirs, coinciden siempre que RSOC exceda el SOC intrínseco, mientras que la presencia de solo un defecto de una sola línea no puede dispersar los electrones dependientes del valle. Cuando están involucrados dos defectos de línea paralela, los nadirs oscilantes evolucionan hacia mesetas de transmisión cero, y se puede realizar una modulación efectiva del transporte dependiente del valle cambiando la periodicidad de oscilación de los dos valles de Dirac con un campo eléctrico perpendicular, donde la periodicidad de oscilación de los dos valles aumentan y disminuyen y conducen a la polarización perfecta del valle en las regiones correspondientes de la meseta amplia de pico cero. En un experimento, se puede detectar una corriente de valle tan pura midiendo el cambio de conductancia con el campo eléctrico. Este fenómeno proporciona una ruta diferente para modular eficazmente la polarización del valle en dispositivos de silicio mediante la utilización de RSOC y campos eléctricos.
Métodos
Comencemos con el esquema de un dispositivo de defecto de línea de silicio de dos terminales, como se muestra en la Fig. 1a, en el que se ilustra la precesión de espín para generar la corriente polarizada en valle debido al RSOC y al campo eléctrico. Se supone que RSOC existe en un lado del defecto de línea con ancho W y WR en unidades de \ (\ sqrt {3} a \), donde a =3.86 Å es la constante de celosía del siliceno prístino, como se muestra en la Fig. 1a. Cuando la energía de Fermi se encuentra en la parte inferior de la banda de conducción, los estados ( K , ↓ ) [( K , ↓ ) corresponde a un estado en el valle K con ↓ (abajo) girar] y ( K ′ , ↑ ) están en la brecha debido a la manipulación de la banda de energía de RSOC. Los otros dos estados, ( K , ↑ ) y ( K ′ , ↓ ), circulan a lo largo del pseudoborde debido a la característica de bloqueo del momento de giro del SOC [24], como se muestra en la Fig. 1a. Para un estado de giro definido, fluye a lo largo del pseudoborde con direcciones opuestas en ambos lados del defecto de línea que puede actuar como un filtro y restringir la transmisión a través del defecto de línea, como se muestra en la Fig. 1c.
Se utiliza un modelo de celosía en la representación de unión estrecha para describir el sistema de defectos de línea con RSOC como [17, 22]
$$ \ begin {array} {@ {} rcl @ {}} H &=&t \ sum _ {\ langle i, j \ rangle \ alpha} c_ {i \ alpha} ^ {\ dag} c_ {j \ alpha} + \ tau_ {2} \ sum _ {\ langle \ gamma \ delta \ rangle \ alpha} c_ {i_ {y} \ alpha, \ gamma} ^ {\ dag} c_ {i_ {y} \ alpha, \ delta} + \ tau_ {1} \ sum _ {\ langle i, \ gamma \ rangle \ alpha} c_ {i \ alpha} ^ {\ dag} c_ {i_ {y} \ alpha, \ gamma} \\ &+ &i \ frac {t_ {so}} {3 \ sqrt {3}} \ sum _ {\ langle \ langle i, j \ rangle \ rangle \ alpha \ beta} \ nu_ {ij} c ^ {\ dag} _ {i \ alpha} \ sigma_ {\ alpha \ beta} ^ {z} c_ {j \ beta} + \ Delta_ {z} \ sum_ {i \ alpha} \ mu_ {i} c_ {i \ alpha} ^ {\ dag} c_ {i \ alpha } \\ &+ &it_ {R} \ sum _ {\ langle i, j \ rangle \ alpha \ beta} c_ {i \ alpha} ^ {\ dag} (\ vec {\ sigma} \ times \ mathrm {\ mathbf { d_ {ij}}}) ^ {z} _ {\ alpha \ beta} c_ {j \ beta} + Hc, \ end {matriz} $$ (1)donde \ (c_ {i \ alpha} ^ {\ dag} \) y \ (c_ {i_ {y} \ alpha, \ gamma / \ delta} ^ {\ dag} \) representan el operador de creación de electrones con spin α en el sitio de silicene i y el defecto de línea, respectivamente, y 〈〉 / 〈〈 〉〉 se extiende sobre todos los sitios de salto de vecino más cercano / siguiente más cercano. Los primeros tres términos denotan el salto del vecino más cercano y los parámetros t , τ 1 y τ 2 denotar varias energías de salto del vecino más cercano en el modelo de unión estrecha, como se muestra en la Fig. 1b. El cuarto término es el SOC efectivo con el parámetro de salto t tan y ν ij =± 1 para saltar en el sentido contrario a las agujas del reloj (en el sentido de las agujas del reloj) entre los siguientes sitios vecinos más cercanos con respecto a la z positiva -eje. Una investigación teórica [16] ha demostrado que los dos átomos de Si más cercanos en la región del defecto son relativamente idénticos a los de la región prístina y que todos los átomos de Si permanecen en la sp 2 - sp 3 estado hibridado. Por lo tanto, es razonable establecer τ 2 = τ 1 = t . En el quinto término, Δ z es el potencial de subred escalonado que surge de un campo eléctrico perpendicular a la hoja de silicene, y μ i =± 1 para la A ( B ) sitio. El último término representa el término RSOC extrínseco donde t R es el parámetro de salto de órbita giratoria de Rashba. d ij es el vector unitario que apunta desde el sitio j a i y \ (\ vec {\ sigma} =(\ sigma ^ {x}, \ sigma ^ {y}, \ sigma ^ {z}) \) en la ecuación. 1 es el vector de matrices de Pauli de espín real. El RSOC surge del potencial externo aplicado ya sea por una puerta eléctrica, adsorción de átomos de metal o sustratos [20, 25] que pueden romper drásticamente la simetría de inversión de la estructura del silicene. En particular, el RSOC extrínseco que se origina en el campo eléctrico se ignora porque es muy débil.
Los ELD de silicene se muestran en la Fig. 1a, que se extiende inmensamente a lo largo de la y dirección. La simetría de traslación de la estructura de celosía a lo largo de y dirección indica que k y es una cantidad conservada y que los operadores de creación (aniquilación) se pueden reescribir de la siguiente manera, de acuerdo con la transformación de Fourier (se ignora el índice de giro) [17]:
$$ \ begin {array} {@ {} rcl @ {}} c_ {i} ^ {\ dag} =\ sum_ {k_ {y}} c_ {k_ {y}, i_ {x}} e ^ {- 2ik_ {y} i_ {y} a}, c_ {i} =\ sum_ {k_ {y}} c_ {k_ {y}, i_ {x}} e ^ {2ik_ {y} i_ {y} a}, \\ c_ {i_ {y}, \ gamma} ^ {\ dag} =\ sum_ {k_ {y}, \ gamma} c ^ {\ dag} _ {k_ {y}, \ gamma} e ^ {- 2ik_ {y} i_ {y} a}, c_ {i_ {y}, \ gamma} =\ sum_ {k_ {y}, \ gamma} c_ {k_ {y}, \ gamma} e ^ {2ik_ {y} i_ {y} a}. \ end {matriz} $$ (2)Entonces, la matriz hamiltoniana de la ecuación. 1 está desacoplado en \ (H =\ sum _ {k_ {y}} H_ {k_ {y}} \), donde \ (H_ {k_ {y}} \) se puede describir de la siguiente forma:
$$ {\ begin {alineado} H_ {k_ {y}} =- \ sum_ {i} \ varphi_ {i, 1} ^ {\ dag} \ hat {T} _ {11} \ varphi_ {i, 1} - \ sum_ {i} \ varphi_ {i, 2} ^ {\ dag} \ hat {T} _ {22} \ varphi_ {i, 2} \\ - \ sum_ {i} \ varphi_ {i, 1} ^ {\ dag} \ hat {T} _ {12} \ varphi_ {i, 2} - \ sum_ {i \ neq-1} \ varphi_ {i, 2} ^ {\ dag} \ hat {T} _ {23 } \ varphi_ {i + \ hat {x}, 1} \\ - \ varphi _ {\ bar {1}, 2} ^ {\ dag} \ hat {T} _ {\ bar {1} 0} \ varphi_ {0 } - \ varphi_ {0} ^ {\ dag} \ hat {T} _ {01} \ varphi_ {1,1} - \ varphi_ {0} ^ {\ dag} \ hat {T} _ {00} \ varphi_ {0} - \ varphi _ {\ bar {1}, 2} ^ {\ dag} \ hat {T} _ {\ bar {1} 1} \ varphi_ {1,1} + hc, \ end {alineado}} $$ (3)donde \ (\ varphi _ {i, l} ^ {\ dag} =\ left [c _ {{{k} _ {y}}, i, l, A \ uparrow} ^ {\ dag}, c _ {{{ k} _ {y}}, i, l, A \ flecha hacia abajo} ^ {\ dag}, c _ {{{k} _ {y}}, i, l, B \ uparrow} ^ {\ dag}, c_ { {{k} _ {y}}, i, l, B \ flecha hacia abajo} ^ {\ dag} \ right] \), i en el conjunto de índice ( i, l ) representa la posición de una supercélula \ ((\ bar {i} =- i) \), y l =1 o 2 denota diferentes cadenas en zigzag en una supercélula, como se muestra en el rectángulo punteado de la Fig. 1b. \ (\ hat {T_ {ll '}} \) representa la matriz hamiltoniana de cada cadena en zigzag ( l = l ′ ) en una supercélula o la interacción entre diferentes cadenas en zigzag ( l ≠ l ′ ).
Se observa que los dos valles K y K ′ ahora se emiten a [0, ± π / 3 a ] debido a la inserción del defecto de línea. La matriz de transmisión del η ( η = K / K ′ ) valle se calcula utilizando la fórmula de Landauer generalizada [26, 27],
$$ \ begin {array} {@ {} rcl @ {}} T ={\ left (\ begin {array} {cc} T ^ {\ uparrow \ uparrow} _ {\ eta} &T ^ {\ uparrow \ flecha hacia abajo} _ {\ eta} \\ T ^ {\ flecha hacia abajo \ uparrow} _ {\ eta} &T ^ {\ flecha hacia abajo \ flecha hacia abajo} _ {\ eta} \ end {matriz} \ right)} =\ sum_ {i , j =1} ^ {8} {\ left (\ begin {array} {cc} \ vert t_ {ij, \ eta} ^ {\ uparrow \ uparrow} \ vert ^ {2} &\ vert t_ {ij, \ eta} ^ {\ uparrow \ downarrow} \ vert ^ {2} \\ \ vert t_ {ij, \ eta} ^ {\ downarrow \ uparrow} \ vert ^ {2} &\ vert t_ {ij, \ eta} ^ {\ flecha abajo \ flecha abajo} \ vert ^ {2} \ end {matriz} \ derecha)}, \ end {matriz} $$ (4)donde
$$ \ begin {matriz} {@ {} rcl @ {}} t =2 \ sqrt {-Im \ Sigma_ {L}} G ^ {r} \ sqrt {-Im \ Sigma_ {R}} \ end {matriz } $$ (5)y
$$ \ begin {array} {@ {} rcl @ {}} t_ {ij, \ eta} ^ {\ uparrow \ uparrow} &=t_ {2 (i-1) +1,2 (j-1) + 1} \\ t_ {ij, \ eta} ^ {\ uparrow \ downarrow} &=t_ {2 (i-1) + 1,2j} \\ t_ {ij, \ eta} ^ {\ downarrow \ uparrow} &=t_ {2i, 2 (j-1) +1} \\ t_ {ij, \ eta} ^ {\ flecha abajo \ flecha abajo} &=t_ {2i, 2j}. \ end {matriz} $$ (6)Aquí, \ (- Im \ Sigma _ {L, R} =- \ left (\ Sigma _ {L, R} ^ {r} - \ Sigma _ {L, R} ^ {a} \ right) / 2i \ ) son matrices semidefinidas positivas con una raíz cuadrada de matriz bien definida, donde \ (\ Sigma _ {L, R} ^ {a} =\ left [\ Sigma _ {L, R} ^ {r} \ right] ^ { \ dag} \) son la auto-energía retardada / avanzada de la derivación izquierda / derecha. La submatriz G de 16 × 16 r es la función de Green retardada, que conecta la primera y la última supercélula a lo largo de la x dirección y se puede calcular utilizando el método de función recursiva de Green. Los coeficientes de transmisión total de η valle son \ (T _ {\ eta} =T ^ {\ uparrow \ uparrow} _ {\ eta} + T ^ {\ uparrow \ downarrow} _ {\ eta} + T ^ {\ downarrow \ uparrow} _ {\ eta } + T ^ {\ downarrow \ downarrow} _ {\ eta} \), y la polarización de espín P s y polarización de valle P η puede ser dado por
$$ {\ begin {align} P_ {s} &=\ frac {T_ {K} ^ {\ uparrow \ uparrow} + T_ {K} ^ {\ uparrow \ downarrow} -T_ {K} ^ {\ downarrow \ flecha abajo} -T_ {K} ^ {\ flecha abajo \ uparrow} + T_ {K '} ^ {\ uparrow \ uparrow} + T_ {K'} ^ {\ uparrow \ downarrow} -T_ {K '} ^ {\ flecha abajo \ flecha abajo} -T_ {K '} ^ {\ flecha abajo \ uparrow}} {T_ {K} + T_ {K ^ {\ prime}}}, \\ P _ {\ eta} &=\ frac {T_ {K} -T_ {K ^ {\ prime}}} {T_ {K} + T_ {K ^ {\ prime}}}. \ end {alineado}} $$Resultados y discusión
En los cálculos de los coeficientes de transmisión dependientes del giro, establecemos τ 2 = τ 1 = t =1 como unidad de energía, la fuerza del SOC t tan =0,005 t y la energía Fermi E f =1.001 t tan , que se encuentra en la parte inferior de la banda de conducción. El ancho de la región de dispersión es W =1000 para el defecto de línea única y un ancho adicional WR =1000 también se tiene en cuenta para los dos defectos de línea paralela, como se muestra en la Fig. 1a.
La Figura 2 muestra los coeficientes de transmisión de spin-conserved / spin-flip del valle \ (\ eta, T ^ {sc} _ {\ eta} / T ^ {sf} _ {\ eta} \), en función del incidente ángulos α (a) y de la fuerza RSOC t R (b – d). Las figuras 2a-c corresponden al caso del defecto de línea única y (d) es para el caso de los dos defectos de línea paralela. Se muestra que en un t definido R (por ejemplo, t R =5 t tan como en la Fig. 2a), los coeficientes de transmisión dependientes del espín \ (T ^ {sc} _ {K} / T ^ {sf} _ {K} \) son constantes e independientes de los ángulos incidentes debido a la relación de dispersión parabólica , como se muestra en la Fig. 2a. Por lo tanto, en los siguientes cálculos, podemos usar el ángulo de incidencia α =0 como ejemplo. Para una t débil R , un fenómeno oscilante similar al de un gas de electrones bidimensionales [26, 27] aparece debido a la división de Rashba, como se muestra en el recuadro de la Fig. 2b. Como t R aumenta ( t R > t tan ), \ (T_ {K} ^ {\ uparrow \ uparrow} \) y \ (T_ {K} ^ {\ uparrow \ downarrow} \) tienen la misma periodicidad oscilante y casi las mismas magnitudes que t R que consta de algunos picos de oscilación y nadirs, mientras que \ (T_ {K} ^ {\ downarrow \ downarrow} / T_ {K} ^ {\ downarrow \ uparrow} \) tiende a cero porque la energía de Fermi se encuentra en su espacio, como mostrado en la Fig. 2b. Por lo tanto, el coeficiente de transmisión total de K El valle es contribuido principalmente por el estado de giro. De hecho, las imágenes de oscilación de los dos valles, K y K ′ , coinciden mientras que los coeficientes de transmisión de K ′ valle es contribuido principalmente por los electrones de spin-down.
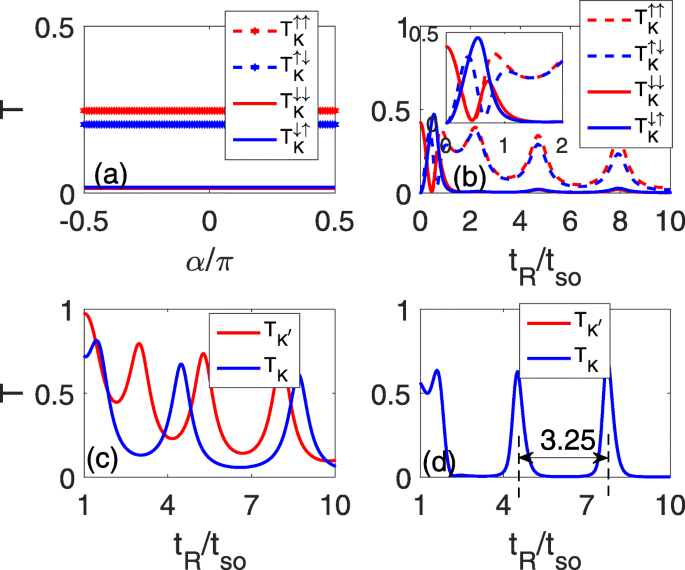
Coeficientes de transmisión spin-conserved y spin-flip como funciones de los ángulos de incidencia α en t R =5 t tan en a y como funciones de la fuerza RSOC t R en b - d , donde a - c son para el defecto de una sola línea y d es para los dos defectos de línea paralela, con Δ z =0,2 t tan en c
En presencia de un campo eléctrico perpendicular, la degeneración del valle se levanta y los comportamientos oscilantes de los dos valles difieren:la periodicidad oscilante del K valle aumenta, mientras que el de K ′ el valle disminuye, como se muestra en la Fig. 2c. Sin embargo, no parece factible filtrar un estado de valle cónico con un solo defecto de línea porque los nadirs oscilantes tienen una magnitud definida. Naturalmente, se puede considerar el fenómeno de oscilación con dos defectos de línea paralela para restringir aún más la transmisión, como se muestra en la Fig. 2d. La comparación de la Fig. 2b con d revela que el pico de oscilación se vuelve estrecho y agudo, mientras que el nadir de oscilación se ensancha y debilita, lo que forma la plataforma de transmisión cero. El espacio entre dos picos de oscilación vecinos se fija en 3,25 t tan , como se caracteriza por las dos líneas punteadas en la Fig. 2d.
Para lograr un mejor efecto de filtro de valle, concentramos nuestra atención en el efecto del campo eléctrico perpendicular. Los resultados de este efecto se muestran en la Fig. 3. Como se discutió anteriormente, la periodicidad de oscilación de los dos valles cambia de manera opuesta, y los picos de oscilación superpuestos originales en la Fig. 2d se alivian. Mientras tanto, la meseta de transmisión cero se amplía y se estrecha para T K y \ (T_ {K ^ {\ prime}} \), respectivamente, como se muestra en la Fig. 3a y b. En Δ z =0,15 t tan , el espacio entre los dos picos de oscilación vecinos se convierte en 3,6 t tan para T K , mientras que se reduce a 3,1 t tan para \ (T_ {K ^ {\ prime}} \), como lo indican las dos líneas discontinuas azul y roja que se muestran en la Fig. 3a. A medida que el campo eléctrico se fortalece, el espacio entre los dos picos de oscilación vecinos continúa aumentando / disminuyendo para T K / \ (T_ {K ^ {\ prime}} \), que es 5.4 t tan /2.8t tan en Δ z =0,3 t tan , como se muestra en la Fig. 3b. El cambio en la periodicidad de la oscilación conducirá a las regiones correspondientes de meseta ancha pico-cero, donde la polarización de valle perfecta con P η =± 1 mesetas se pueden realizar, como se muestra en la Fig. 3c y d. Simultáneamente, se muestra que la alta polarización de espín P s también surge cuando P η =± 1.
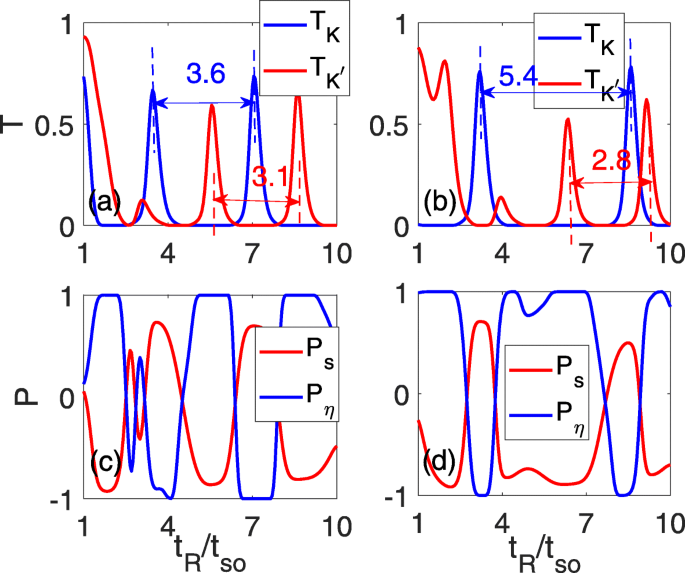
Los coeficientes de transmisión totales \ (T_ {K} / T_ {K ^ {\ prime}} \) ( a , b ) y la polarización de espín / valle ( c , d ) en función de la fuerza de RSOC t R para diferentes potenciales de subred. Δ z =0,15 t tan en a y c y Δ z =0,3 t tan en b y d ; los otros parámetros son idénticos a los de la Fig. 2d
Sin embargo, debido a la incontrolabilidad de RSOC, todavía es difícil detectar tales corrientes de valle puras experimentalmente, a pesar de que el RSOC inducido en el defecto de línea puede ser mayor que el SOC intrínseco. Para sondear convenientemente la corriente de valle pura de forma experimental, también investigamos los coeficientes de transmisión y la polarización del valle en función del campo eléctrico, que se puede controlar continuamente durante un experimento. Se muestra que la polarización de valle perfecta con P η =± 1 puede emerger en un cierto rango de Δ z y que puede cambiar de P η =1 a P η =−1 a medida que aumenta el campo eléctrico, como se muestra en la figura 4a. Para un t definido R (por ejemplo t R =7.2 t tan , como se indica con una línea discontinua en la Fig. 4a), los coeficientes de transmisión \ (T_ {K} / T_ {K ^ {\ prime}} \) oscilan con Δ z , donde los picos de transmisión de la K ( K ′ ) valle corresponden a las mesetas de transmisión cero del K ′ ( K ) Valle. Los coeficientes de transmisión totales son básicamente aportados por un valle a medida que varía el campo eléctrico, y la polarización de valle perfecta siempre puede ocurrir alrededor del valor máximo de \ (T_ {K} / T_ {K ^ {\ prime}} \), como se muestra en Figura 4b. A medida que la energía de Fermi se aleja del borde de la banda, la polarización de valle perfecta aún puede sobrevivir incluso en E f =1,5 t tan , donde la relación de meseta se puede mantener bien, como se muestra en la Fig. 4c. Durante un experimento, se pueden analizar las corrientes eléctricas polarizadas en valle del cable de izquierda a derecha con una cantidad medible experimentalmente, como la conductancia, que es proporcional al coeficiente de transmisión total. La conductancia máxima entre dos valores mínimos (a veces, son cero) debe ser de un valle. Podemos estimar la magnitud de la conductancia de acuerdo con la fórmula \ (G =\ frac {e ^ {2}} {h} \ int _ {- k_ {F}} ^ {k_ {F}} T \ frac {dk_ {y}} {2 \ pi / L_ {y}} =\ frac {e ^ {2}} {h} \ frac {Ly \ sqrt {E ^ {2} -t ^ {2} _ {so}} } {2 \ pi \ hbar v_ {F}} 2T \) [28], donde L y =2 a ≈7.72Å es el ancho del defecto de la línea de silicio, v F =5,5 × 10 5 m / s es la velocidad de Fermi, \ (\ hbar =h / 2 \ pi \) es la constante de Planck reducida con \ (\ phantom {\ dot {i} \!} h =4.13566743 \ times 10 ^ {- 15} eV \ cdot s, T =T_ {K} + T_ {K '} \) es el coeficiente de transmisión total y E es la energía in situ de los electrones incidentes. Entonces, la conductancia es aproximadamente \ (G \ approx \ left [0.7T \ sqrt {E ^ {2} -t ^ {2} _ {so}} / eV \ right] \ frac {e ^ {2}} { h} \). También se encuentra que a medida que la energía in situ en el lado del incidente se eleva a E =0,15 t ( t =1.6 eV ), los coeficientes de transmisión de los dos valles cambian solo un poco en comparación con la Fig. 4c debido a la conservación del giro y el momento y la relación pico de transmisión-meseta cero se mantiene estable, como se muestra en la Fig. 4d. En este caso, la conductancia es aproximadamente \ (G \ approx 0.17T \ frac {e ^ {2}} {h} \) que es considerable y puede detectarse en el experimento. La ventana de energía para observar este fenómeno es de aproximadamente 0,5 t tan ( t tan < E <1,5 t tan ) que es proporcional a t tan . En el experimento, no es difícil controlar la energía de Fermi cerca del borde de la banda y la brecha de SOC incluso se puede aumentar radicalmente a 44 meV por proximidad con Bi (111) bicapa [29] que puede mejorar en gran medida la región de energía para detectar el puro corriente del valle. Además, el modelo computacional también puede ser aplicable a otras contrapartes de bajo pandeo de grafeno, germanene [30], stanene y MoS 2 [31-36], que tienen ranuras de banda aún mayores [37, 38], así como las fortalezas del SOC (la fuerza del SOC puede alcanzar 0.1eV para el stanene [38, 39]). En un experimento real, es fácil realizar un RSOC fuerte que puede superar el SOC intrínseco rompiendo la simetría especular en el plano con el sustrato especial [40]. Por lo tanto, este esquema puede ser completamente factible en el experimento.
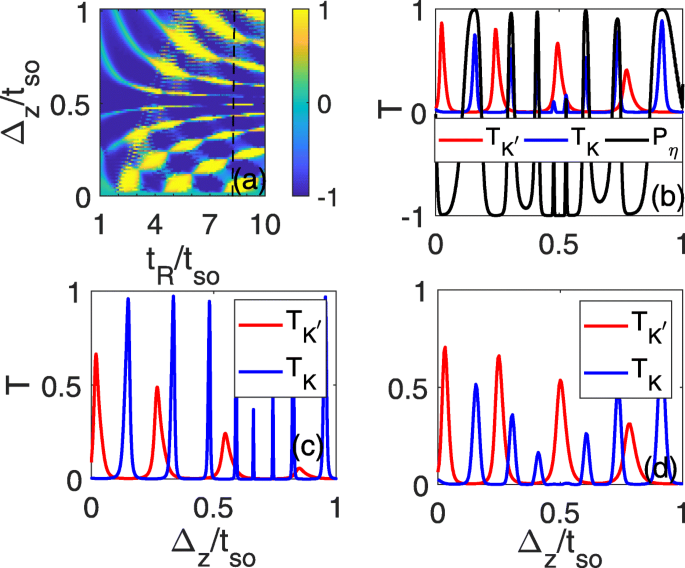
Polarización del valle a y \ (T_ {K} / T_ {K ^ {\ prime}} \) ( b - d ) como funciones de Δ z y t R . t R =7.2 t tan en ( b - d ), E f =1,5 t tan en c y d , y la energía en el sitio es E =0,15 t en el electrodo izquierdo en d ; todos los demás parámetros son idénticos a los de la Fig. 2d
Conclusiones
Hemos propuesto un método eléctrico para generar una corriente polarizada en valle en defectos de línea de silicio. En marcado contraste con los enfoques eléctricos convencionales que se utilizan para producir corriente polarizada en valle, exploramos el RSOC, que se considera que sintoniza la polarización de espín ampliamente utilizada en los FET con polarización de espín. Se encuentra que los coeficientes de transmisión de los dos valles oscilan con la misma periodicidad e intensidad, que se compone de picos de transmisión y mesetas de transmisión cero. La corriente polarizada en valle se puede generar sintonizando la periodicidad de oscilación de los dos valles con un campo eléctrico, que puede destruir la simetría de los estados del valle y provocar las correspondientes regiones de meseta de pico cero de transmisión. Además, también proporcionamos un esquema para detectar la corriente de valle pura en el experimento y los resultados pueden arrojar luz sobre la manipulación de corrientes de polarización de valle por medios eléctricos.
Disponibilidad de datos y materiales
Los conjuntos de datos generados durante y / o analizados durante el estudio actual están disponibles de los autores correspondientes a solicitud razonable.
Abreviaturas
- 2D:
-
Bidimensional
- ELD:
-
Defecto de línea extendida
- FET:
-
Transistor de efecto de campo
- RSOC:
-
Acoplamiento Rashba spin-órbita
- SOC:
-
Acoplamiento intrínseco espín-órbita
Nanomateriales
- Medición del nivel de fluido sin contacto utilizando un chip reflectómetro
- Cómo inicializar RAM desde un archivo usando TEXTIO
- Avanzando hacia 7nm
- Uso de ángulos para mejorar el futuro de la electrónica
- Hormigón inteligente con nanopartículas
- Tipos de datos de C# con ejemplo:Aprenda Int | Flotador | Doble | Carbonizarse
- Inicio de sesión de Facebook usando Python:Ejemplo de inicio de sesión de FB
- Fabricación de alto rendimiento de nanofibras de calidad utilizando un electrohilado de superficie libre modificado
- Defectos de Fundición:Tipos, Causas y Remedios
- Prevención de problemas y defectos de soldadura mediante el uso de metales verificados
- 5 formas de bajo costo para comenzar a utilizar la automatización industrial 4.0 para mejoras de línea



