Una bomba de agua nanométrica inducida por el movimiento browniano y no browniano de una hoja de grafeno en una superficie de membrana
Resumen
La bomba de agua que ahorra energía y las membranas semipermeables eficientes son los núcleos de la tecnología de ósmosis inversa. Aplicar nanotecnología para mejorar el rendimiento está de moda en los últimos años. Basándonos en el efecto competitivo de la infiltración espontánea del agua de dos lados de un nanotubo de carbono, diseñamos una bomba de agua que aprovecha la permeabilidad natural debilitando la competitividad de un lado a partir de una pequeña hoja de grafito colocada sobre la membrana. Según las simulaciones de dinámica molecular, se observa un flujo neto continuo. El modo de movimiento de la hoja es la clave para el desempeño. Para el movimiento browniano puro sin ninguna carga dinámica, encontramos dos moléculas de agua por flujo de nanosegundo, mientras que el flujo inducido por el movimiento unidireccional puede incrementarse varias veces, dependiendo de la fuerza externa. El movimiento browniano es similar al mecanismo físico de la presión osmótica, y el movimiento unidireccional muestra un gran rendimiento que tiene grandes aplicaciones para la ósmosis inversa. Nuestro trabajo propone de manera creativa una nueva estrategia para bombear moléculas de agua que atraviesan un nanocanal, lo que inspira a los diseñadores de dispositivos nanofluídicos.
Antecedentes
La desalinización de agua de mar es una dirección de resaltado para resolver la escasez mundial de agua, ya que, en teoría, puede ofrecer un sinfín de agua limpia. Sin embargo, la tecnología actual no es perfecta. Hay dos métodos diferentes para la desalación de agua de mar. La primera es la destilación, obteniendo agua pura calentando agua de mar y luego enfriando los vapores. El cambio de fase puede eliminar completamente las impurezas, pero consume mucha energía y es costoso. La otra es la ósmosis inversa (RO), que impulsa el agua de mar a través de una membrana semipermeable que es permeable al agua pero impermeable a los iones. Se beneficia de la mejora de las membranas semipermeables y las bombas de agua a presión, la RO está madura y se utiliza ampliamente [1]. Sin embargo, la RO sigue consumiendo mucha energía [2, 3, 4]. Esto se debe a que el sistema de ósmosis inversa necesita mantener una caída de presión alta para compensar la presión permeable e impulsar el agua de mar a través de membranas semipermeables. Muchos científicos creen que “para que la desalinización esté a la altura de los desafíos del agua del siglo XXI, se necesita un cambio radical en la tecnología de membranas de OI” [5]. Proponen que los nanotubos de carbono (CNT) son un canal de agua ideal con ventajas como selectividad, alta eficiencia y bajo costo energético [6] y tienen un gran potencial para aplicaciones como canales nanofluídicos [7,8,9,10]. Sin embargo, solo mejorar la propiedad de la membrana de OI es útil para la eficacia de la OI, pero es inútil para ahorrar energía, ya que la desalinización por OI actual ya se ha acercado a la limitación termodinámica [4]. Se necesitan métodos de conducción más eficientes como alternativas a la bomba de alta presión [11].
Para un canal de CNT que conecta dos depósitos de agua, las moléculas de agua siempre pueden ingresar al canal de manera espontánea debido al movimiento browniano. Sin embargo, los efectos de infiltración de dos lados del canal de CNT se compensan entre sí, ya que no existe un flujo de agua neto. Dado que el flujo neto se considera el resultado de la competencia del movimiento browniano de dos lados del canal CNT, mejorar o debilitar la competitividad de un lado debería ser un método eficaz para bombear agua. En trabajos anteriores, la caída de presión [12, 13], la diferencia de temperatura [14, 15] y el campo eléctrico [16] son estrategias comunes para mejorar la competitividad en un lado para crear un flujo de agua neto. No obstante, debilitar la competitividad parece ser una mejor opción ya que hacemos uso de la permeabilidad natural.
En realidad, controlar el transporte de nanofluidos es relevante para aplicaciones generalizadas, que van desde almacenamientos de energía hasta biosensores [17,18,19,20,21,22,23], lo que sigue siendo un desafío. Aquí, diseñamos una nueva bomba de agua con una pequeña hoja de grafito en un lado de la membrana con el objetivo de romper el equilibrio del movimiento browniano de los dos depósitos, asemejándose a un sistema de rotura simétrico. La hoja tiene dos modos de movimiento:movimiento térmico y movimiento unidireccional, correspondientes a los movimientos brownianos y no brownianos, respectivamente. Mediante cálculos de simulación, se logra debilitar la competitividad del lado superior y se induce un flujo de agua de abajo hacia arriba. Además, para el movimiento browniano, la cantidad de flujo de agua es de casi dos por nanosegundo que está cerca de la acuaporina [24, 25], lo que sugiere posibles aplicaciones en membranas biológicas. La hoja pequeña impulsa el agua desde el lado de abajo hacia arriba a través del CNT, lo que puede ser una analogía con el mecanismo físico de la presión osmótica. Además, en el movimiento unidireccional, la cantidad de flujo se puede aumentar significativamente varias veces, dependiendo de la velocidad de movimiento de la hoja o de la fuerza externa. A medida que la tecnología entra en operación a escala molecular, como la manipulación de nanopartículas superficiales con pinzas ópticas [26] y microscopía de fuerza atómica [27], nuestro trabajo muestra una probabilidad de ajustar la simetría de permeabilidad del agua, lo que abre un nuevo método para la bomba de agua.
Modelo y método de simulación
En la Fig. 1 se muestra una instantánea del sistema de simulación. Utilizamos un (6, 6) CNT (longitud de 2,56 nm y diámetro de 0,81 nm) y dos láminas de grafito paralelas (5,1 × 5,1 nm 2 ) para componer una membrana permeable. En un canal tan estrecho, las moléculas de agua presentan una disposición de una sola fila [6]. Una pequeña hoja de grafito formada por 272 átomos de carbono se coloca en la membrana de cerca. La fuerte interacción carbono-carbono conduce a la adsorción de una pequeña hoja en la membrana. De hecho, durante el proceso de nuestras simulaciones, la distancia media entre la lámina y la membrana es de aproximadamente 0,34 nm. En el movimiento browniano, establecemos la temperatura de la pequeña hoja de grafito en un rango de 100 a 500 K. Oscilará en la membrana cerca de la entrada de CNT, chocando con las moléculas de agua cercanas. Tres mil trescientas veintiocho moléculas de agua llenan el canal y dos depósitos. La temperatura del agua se fija en 300 K. Para el modo de movimiento unidireccional, aplicamos una aceleración adicional en cada átomo de carbono de la hoja pequeña para lograr la fuerza adicional, donde 0.1 nm / ps 2 corresponde a 2 pN. La fuerza adicional está a lo largo de x dirección. El flujo de agua es inducido por la asimetría del sistema. Debido a la condición de límite periódica en las tres dimensiones, la hoja pasará continuamente a través de la vecindad de la entrada de CNT e induce un flujo de agua estable y un flujo.
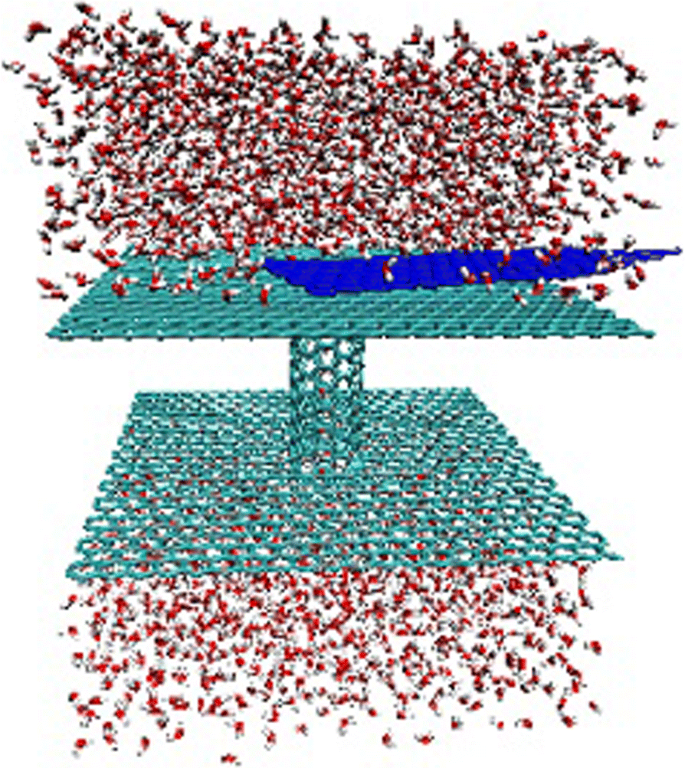
Instantánea del sistema de simulación. Un CNT con una longitud de 2,56 nm y un diámetro de 0,81 nm, que conecta dos depósitos de agua, separados por dos láminas de grafito (verde salvia, 5,1 × 5,1 nm 2 ). Una pequeña hoja de grafito (azul) colocada sobre la grande de cerca. El sistema estaba integrado en una caja de agua periódica con 3328 moléculas de agua, lo que representa una bomba de agua nanométrica
Durante nuestras simulaciones, el sistema estaba en un volumen y temperatura constantes con una caja periódica, y las moléculas de agua eran modelos TIP3P clásicos [28]. Los átomos de carbono eran partículas Lennard-Jones (LJ) sin carga con parámetros de σ cc =0,34 nm, ε cc =0,3612 kJ / mol; σ co =0.3275 nm, ε co =0,4802 kJ / mol [6]. Se empleó el método PME para tratar las interacciones electrostáticas de largo alcance [29]. Las simulaciones se ejecutan 125 ns en el software de Gromacs 4.6.5 [30] con un intervalo de tiempo de 2 fs (datos recopilados cada 1 ps), y se recopilaron los últimos 120 ns. Se realizaron dos simulaciones independientes para reducir el error.
Resultados y discusión
El movimiento browniano de una hoja de grafito
Al principio, estudiamos el modo de movimiento browniano de la hoja a diferentes temperaturas. Para medir la capacidad de inducir el flujo de agua a través de los CNT, siguiendo el trabajo anterior [31, 32], definimos el flujo ascendente y el flujo descendente como la cantidad de moléculas de agua que conducen a través del tubo a lo largo de + z y - z dirección, respectivamente. Flujo =flujo ascendente + flujo descendente, flujo =flujo ascendente - flujo descendente y eficiencia de transporte unidireccional η se puede calcular con η =Flujo / flujo. El flujo de agua y el flujo en función de la temperatura de la hoja se muestran en la Fig. 2. En nuestra hipótesis original, la hoja caliente calienta el agua alrededor y luego crea una diferencia de temperatura a lo largo del CNT para impulsar el agua a través del canal. Sin embargo, el flujo de agua en las simulaciones es descendente, lo que se opone a lo que esperábamos. Además, el flujo de agua es insensible a la temperatura de la hoja. Además, la fluctuación de temperatura de una hoja pequeña está dentro del alcance de 10 K durante nuestro proceso de simulación. En realidad, debido al control de temperatura de las simulaciones NVT, el intercambio de calor entre la hoja y la solución circundante es débil y puede ignorarse. Como muestra la Fig. 2, siempre podemos obtener un flujo neto continuo a aproximadamente dos moléculas de agua por nanosegundo sin importar cuál sea la temperatura de la hoja, que está cerca del valor experimental de 1.8 en los canales de acuaporina [24, 25], lo que sugiere aplicaciones potenciales en sistemas biológicos. Mientras tanto, el flujo de agua total es casi independiente de la temperatura de la hoja y debería ser similar al caso sin la hoja.
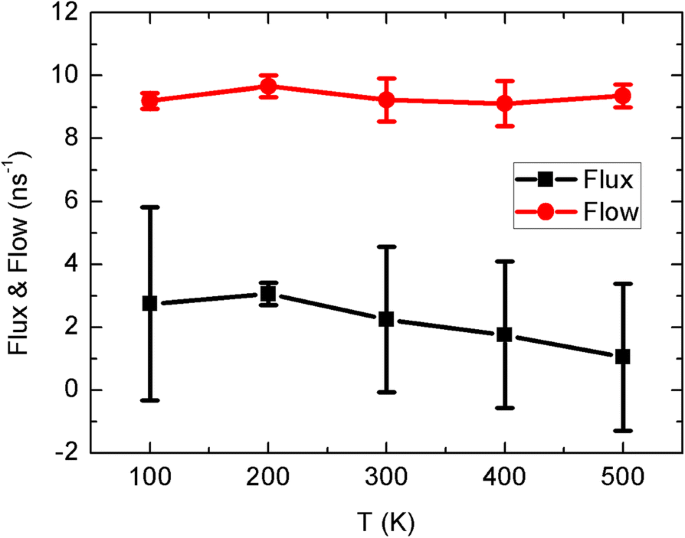
El flujo de agua y el flujo en función de la temperatura de la hoja. Se muestran barras de error para dos puntos de datos
El transporte de agua al sesgo por el movimiento browniano de una nanocapa se asemeja al proceso osmótico. Desde la perspectiva de la dinámica molecular, el flujo de agua neto debería ser causado por la competencia del movimiento browniano de las moléculas de agua cerca de las dos entradas del canal CNT. La hoja pequeña influye en la velocidad de las moléculas de agua por frecuentes colisiones y luego cambia la competitividad. Curiosamente, la hoja se coloca en el lado superior pero induce el flujo de agua de abajo hacia arriba, lo que sugiere que el efecto de la hoja está debilitando la competitividad. Sin embargo, el movimiento browniano de la hoja es irregular y el flujo neto es insensible a la temperatura con grandes fluctuaciones. Por lo tanto, analizaremos más a fondo el modo de movimiento unidireccional de la hoja en la siguiente parte, y se descubren fenómenos más interesantes.
Luego, recopilamos el tiempo de translocación del agua y la ocupación como se ve en la Fig. 3. Aquí, el tiempo de translocación es el tiempo de tránsito promedio de las moléculas de agua a través del canal CNT. Similar al flujo de agua, el tiempo de translocación fluctúa con la temperatura de la hoja. De hecho, el tiempo de translocación debe corresponder al flujo de agua, ya que cuanto más rápido pasan las moléculas de agua a través del canal, mayor debe ser el flujo de agua. No obstante, tal anti-relación está cubierta por la fluctuación termodinámica aquí. En teoría, la ocupación está determinada por la estructura del canal CNT. A medida que se mantiene la cadena de agua de una sola fila, siempre hay cerca de diez moléculas de agua dentro del canal de CNT con ligeras fluctuaciones. Por lo tanto, las fluctuaciones termodinámicas son inevitables pero no notables.
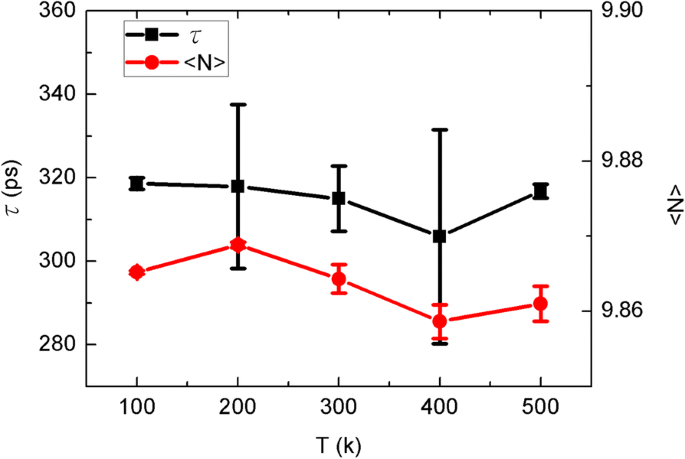
El tiempo de translocación del agua τ y ocupación < N > en función de la temperatura de la hoja
Como las propiedades de dinámica térmica de las moléculas de agua dentro de CNT estrecho es otro tema importante que nos preocupa, las distribuciones de densidad y el número de enlaces de hidrógeno (enlace H) se cuentan como una función de z posición mostrada en la Fig. 4. Aquí, las dos moléculas de agua forman un enlace H cuando su distancia de oxígeno es menor a 0.35 nm y el ángulo entre el enlace O – H y O – O es menor a 30 °. La parte de 2 a 4 nm de z La posición corresponde al canal CNT, donde la densidad y el comportamiento del número de enlaces H es diferente de las áreas a granel. La densidad en el CNT es casi cuatro veces mayor que a granel, lo que implica el potencial de almacenamiento masivo. El patrón ondulado de densidad con diez picos está en línea con la ocupación en la Fig. 3, debido a la estructura única de CNT. El cambio del número de enlaces H también muestra el proceso por el cual una molécula de agua entra en el CNT para formar una cadena de una sola fila con enlaces H reducidos.
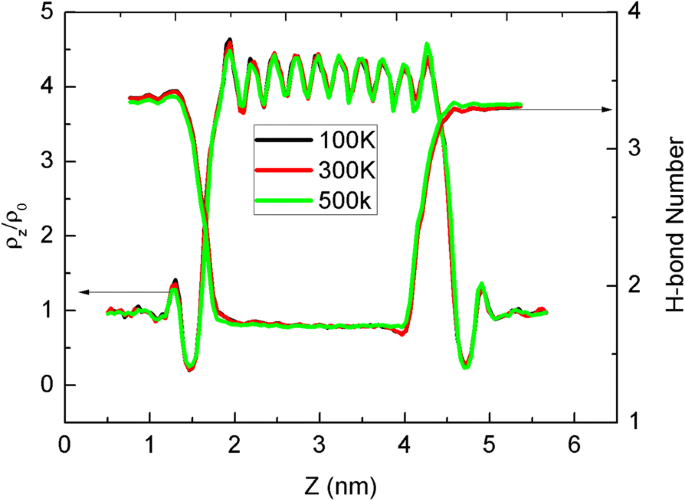
Distribución de densidad y número de enlaces de hidrógeno a lo largo de z El eje y los diferentes colores de línea son para diferentes temperaturas de hoja. Aquí, ρ 0 es de 1,0 g / cm 3 de la densidad aparente del agua
Las moléculas de agua dentro del CNT con orientaciones únicas se han revelado temprano [16]. Aquí, calculamos la distribución de probabilidad de las orientaciones del dipolo de agua como se muestra en la Fig. 5. Para reducir el error, promediamos los datos de las dos simulaciones independientes. <θ> es el ángulo promedio entre el dipolo de agua y el z eje, y hay casi dos estados (20 ° –40 ° y 140 ° –160 °) para las orientaciones del agua. El patrón es casi simétrico con respecto a <θ> =90 °, lo que indica la orientación del dipolo único. En conjunto, el transporte de agua es insensible a la temperatura de la hoja. Esto se debe a que el movimiento browniano de la hoja siempre está en la membrana de grafeno debido a la fuerte interacción hidrófoba hoja-membrana, y el impacto de la hoja es muy limitado. A continuación, analizaremos con más detalle el modo de movimiento unidireccional de la hoja, donde el transporte de agua puede verse afectado de manera más significativa.
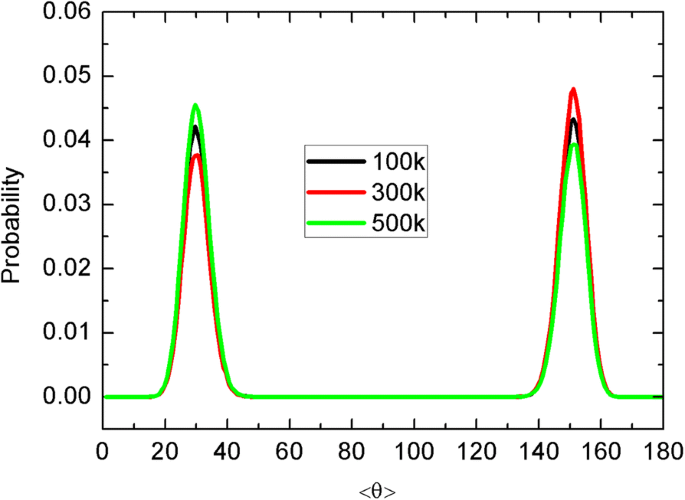
La distribución de probabilidad de la orientación dipolar promedio de las moléculas de agua dentro del CNT y las diferentes temperaturas de la hoja están marcadas por colores de línea
El movimiento unidireccional de una hoja de grafito
Como el movimiento de la hoja debe ser importante para el rendimiento, investigamos más a fondo un modo de movimiento típico no browniano, es decir, el movimiento unidireccional. La hoja es impulsada por una fuerza adicional y se mueve sobre la membrana de grafeno con una velocidad estable. Curiosamente, el flujo de agua, el flujo y la eficiencia del transporte unidireccional η aumenta rápidamente con el aumento de fuerza como se ve en la Fig. 6a. Luego, para describir la dinámica de la hoja, presentamos la ecuación de Langevin unidimensional:
$$ m \ frac {d ^ 2x} {\ mathrm {d} {\ mathrm {t}} ^ 2} =F- m \ xi \ frac {\ mathrm {d} \ mathrm {x}} {\ mathrm { d} \ mathrm {t}} + R (t) $$donde, m es la masa de la hoja, F es la fuerza impulsora, R ( t ) es la fuerza causada por las colisiones aleatorias de moléculas de agua, y ξ es el coeficiente de fricción. Las colisiones aleatorias son complicadas, y aquí, solo contamos R ( t ) como las colisiones mutuamente compensadas y < R ( t )> =0. En estado estable, la hoja mantiene una velocidad uniforme y la fuerza de fricción es igual a la fuerza impulsora. Por lo tanto,
$$ F =m \ xi \ frac {\ mathrm {dx}} {\ mathrm {dt}} =m \ xi v $$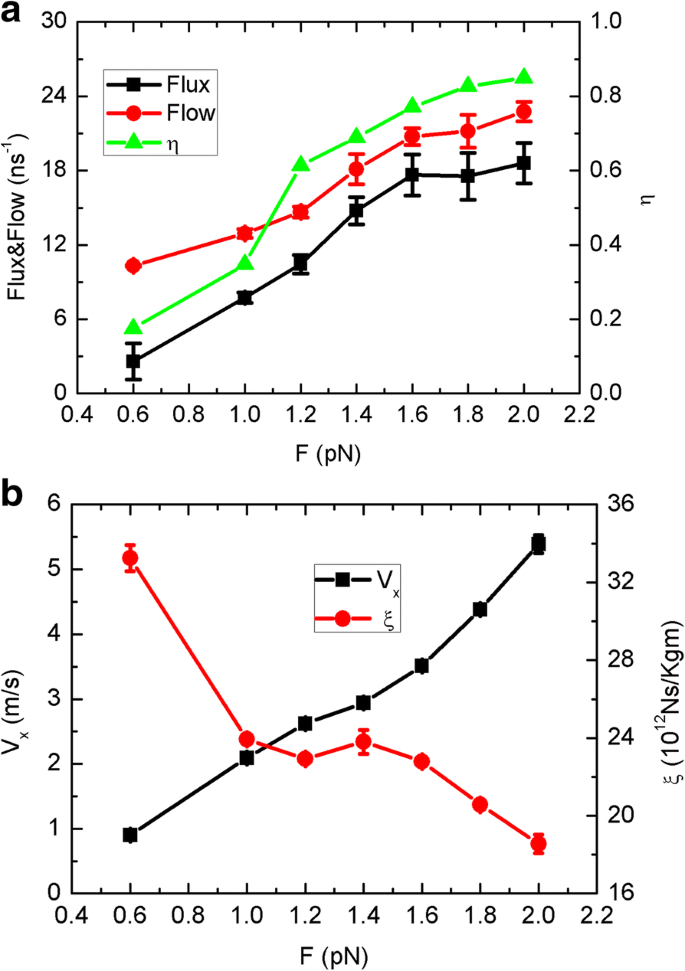
un El flujo de agua, el flujo y la eficiencia unidireccional η y b la velocidad de la hoja V x y coeficiente de fricción ξ en función de la fuerza impulsora F
Mostramos la velocidad (de la trayectoria MD) y el coeficiente de fricción ξ en función de la fuerza motriz en la Fig. 6b. La velocidad aumenta casi linealmente con la fuerza impulsora, correspondiente a los comportamientos de flujo y flujo, mientras que el coeficiente de fricción disminuye en su conjunto. Por lo tanto, el flujo de agua y el flujo deben estar directamente relacionados con la velocidad de la hoja. Desde el punto de vista de la dinámica molecular, a medida que existe el efecto competitivo, la hoja arrastra las moléculas de agua circundantes y debilita la competitividad del lado superior. Cuanto más rápido se mueva la hoja, más débil debería ser la competitividad. A medida que la fuerza supera los 1,6 pN, el flujo tiende a ser suave, cercano a 16 por nanosegundo, que es casi 8 veces más que el modo browniano. Obviamente, este movimiento unidireccional es más eficiente que el movimiento browniano aleatorio. Por lo tanto, la hoja controlada artificialmente es otra estrategia alternativa para la ósmosis inversa, donde la hoja podría ser manipulada por algunas tecnologías experimentales avanzadas como pinzas ópticas [26] y microscopía de fuerza atómica [27].
Sorprendentemente, el aumento de la velocidad de la hoja y la fuerza impulsora conducen al debilitamiento de la competencia del lado superior mucho más que el modo browniano. En un esfuerzo por dilucidar aún más cómo se ve afectado el movimiento del agua, mostramos el tiempo de translocación promedio y la ocupación como una función de la fuerza impulsora en la Fig. 7. Ambos muestran relaciones casi lineales con la fuerza impulsora, a diferencia de los resultados de Fig. 3. La disminución del tiempo de translocación corresponde al comportamiento creciente del flujo de agua en la Fig. 6a, que debería ser causado por el arrastre de la hoja. Desde otro punto de vista, cuando la lámina arrastra las moléculas de agua circundantes, la competitividad térmica del lado superior debe reducirse, facilitando la permeación del agua de abajo hacia arriba a través del canal CNT.
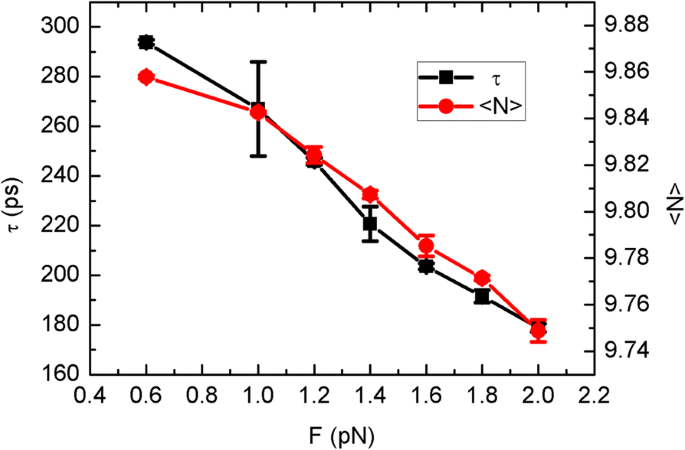
El tiempo de translocación τ y ocupación < N > en función de la fuerza impulsora
Además presentamos los perfiles de densidad del agua, el enlace H y las distribuciones del dipolo de agua en la Fig. 8. Como puede verse en la Fig. 8a, los perfiles de densidad y el enlace H sólo se ven afectados levemente por el movimiento de la hoja. Por ejemplo, bajo la gran fuerza de 1.8 pN, los picos de densidad en forma de onda se reducen y la distribución de enlaces H se vuelve ligeramente asimétrica. Se puede encontrar un cambio similar para la orientación del dipolo de agua en la Fig. 8b. Bajo la condición de equilibrio, por ejemplo, para el movimiento browniano anterior, los dos eventos de orientación ocurren con una probabilidad similar, lo que lleva a una altura de pico similar, como se ve en la Fig. 5. Sin embargo, como hemos discutido, el movimiento unidireccional de la hoja debe tienen más influencia en la cadena de agua que el movimiento browniano. Esto se debe a que la lámina que fluye arrastrará el agua circundante para moverse debido a la interacción de Lennard-Jones entre la lámina y el agua y, por lo tanto, afectará el movimiento u orientación del agua cerca de la entrada de CNT. Por lo tanto, las orientaciones de los dipolos en la Fig. 8b se vuelven asimétricas. Aunque la dinámica y la termodinámica del agua confinada se pueden alterar más profundamente para el movimiento unidireccional, debido a la preservación de la cadena de agua de una sola fila, tal alteración todavía es muy limitada, especialmente para la termodinámica y las características clave de la densidad, enlace H , y dipolo están cerca del caso del movimiento browniano. En consecuencia, diferentes modos de movimiento de la hoja pueden tener un mayor impacto en la dinámica del agua que en la termodinámica.
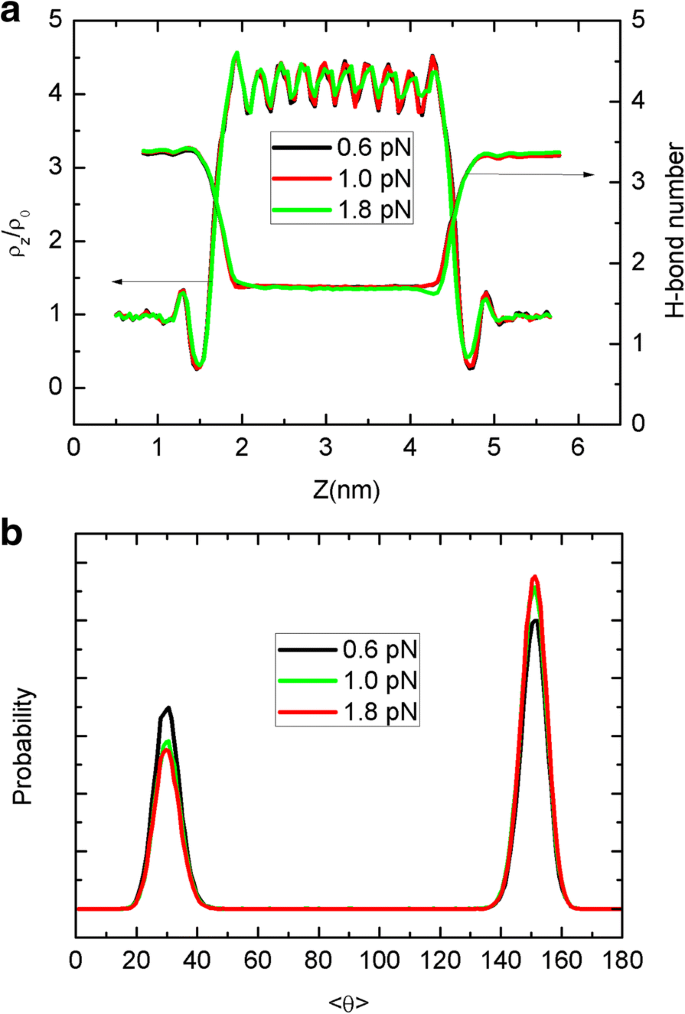
un Los perfiles de densidad del agua axial y el número de enlaces de hidrógeno en función de z posición a lo largo de la CNT para diferentes fuerzas. b Distribución de probabilidad de la orientación dipolar promedio de las moléculas de agua dentro del CNT para diferentes fuerzas
Discusión adicional
Se cree que la distancia inicial entre la hoja de grafeno y la entrada de CNT debería tener un efecto trivial en el flujo de agua y el flujo a través del CNT. De hecho, colocamos aleatoriamente la hoja en la membrana de grafeno superior, donde la hoja se adsorbe directamente en la superficie sin agua en el medio, como se ve en la Fig.1 arriba. De esta forma, la hoja siempre se moverá sobre la superficie debido a la fuerte interacción hidrófoba hoja-membrana, proporcionando un sistema nanofluídico asimétrico. Como se muestra en la Fig. 9, calculamos la distancia media de hoja-membrana y hoja-CNT para los movimientos brownianos y unidireccionales. Llama la atención que la distancia media hoja-membrana esté fijada en 0,34 nm para ambos casos, correspondiendo estrictamente al diámetro potencial de Lennard-Jones carbono-carbono. Por tanto, la hoja siempre se adsorberá sobre la superficie de la membrana. Para el movimiento browniano de la figura 9a, la distancia hoja-CNT también es una constante que es independiente de la temperatura de la hoja. Esto se debe claramente a la interacción hidrofóbica hoja-CNT que conduce a que la hoja se envuelva con respecto al CNT. También debemos tener en cuenta que en nuestra configuración de simulación, la entrada de CNT excede la ubicación de la membrana de grafeno 0.2 nm, y esto puede evitar que la entrada bloquee la entrada. Se cree que si la lámina no se coloca inicialmente sobre la membrana, puede moverse en el depósito al azar y debería tener alguna probabilidad de bloquear la entrada de CNT. Además, para el movimiento unidireccional en la Fig. 9b, la distancia de hoja-CNT exhibe comportamientos crecientes con el aumento de fuerza, correspondiente a los comportamientos de flujo y flujo. Con una fuerza pequeña, la hoja puede quedar atrapada cerca del CNT durante un tiempo, mientras que la fuerza más grande puede acelerar el paso de la hoja, lo que lleva a una distancia mayor. Demasiado, la distancia inicial de hoja-CNT no debería tener un efecto apreciable sobre el flujo de agua y el flujo, mientras que la hoja-membrana podría tener. Sin embargo, si la hoja está inicialmente en agua a granel en lugar de en la membrana, el sistema debería volverse simétrico que difiera de nuestro objetivo inicial, y el fenómeno de transporte de polarización debería desaparecer.
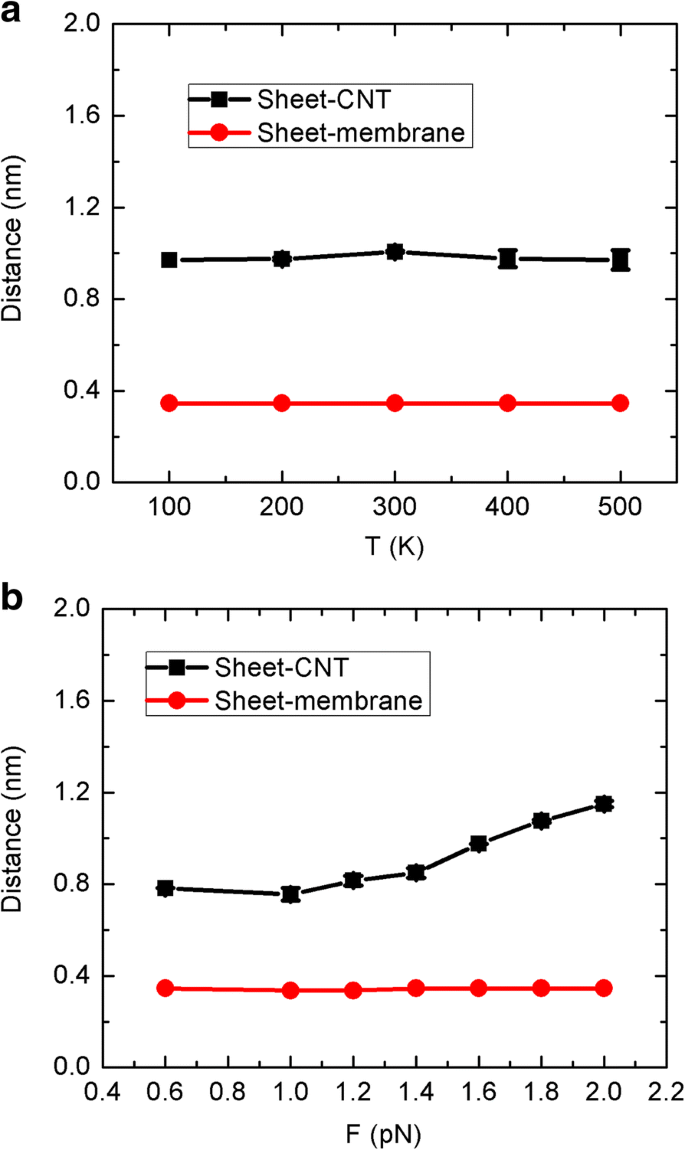
La distancia media de hoja-membrana y hoja-CNT para diferentes condiciones de simulación: a Movimiento browniano y b movimiento unidireccional
Para el movimiento browniano, las temperaturas medias del agua y la hoja durante el proceso de simulación se muestran en la Fig. 10 como una función de la temperatura de la hoja objetivo. Podemos ver que la temperatura media de la hoja se puede controlar estrictamente en sus valores objetivo y, de forma similar, el valor medio del agua también se mantiene en T =300 K. De hecho, usamos el método Nose-Hoover para controlar las temperaturas tanto de la hoja como del agua. Generalmente, en los conjuntos NVT (o NPT) de simulaciones MD, el intercambio de calor entre diferentes moléculas no puede ocurrir debido al termostato. Sin embargo, las colisiones intermoleculares entre la hoja y el agua circundante deberían salir, incluso si finalmente son sintonizadas por el termostato. Las colisiones de la hoja en movimiento pueden afectar la velocidad instantánea o su dirección de las moléculas de agua circundantes y, por lo tanto, en última instancia, cambiar la probabilidad de que el agua entre en el CNT. No obstante, todavía es muy difícil capturar una influencia tan instantánea de la hoja sobre el agua, ya que debería suceder en un tiempo muy corto, posiblemente menos que el tiempo de recolección de datos de 1 ps. Por lo tanto, podemos plantear la hipótesis de que la vibración de la lámina puede afectar la fluctuación térmica del agua circundante y debilitar la competitividad del depósito superior, lo que conduce al fenómeno de transporte de polarización.
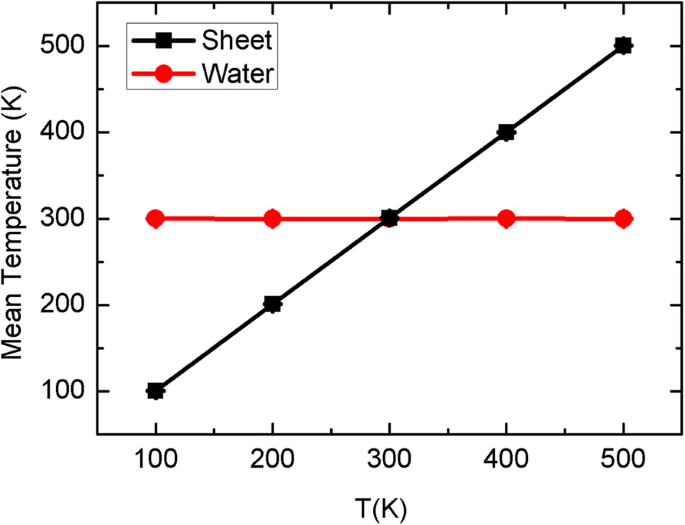
Las temperaturas medias de la hoja y el agua en función de la temperatura de la hoja objetivo
Conclusiones
En resumen, propusimos una nueva estrategia para simulaciones dinámicas de bombas de agua por moléculas y logramos un flujo de agua neto considerable basado en la permeabilidad espontánea del agua. Las moléculas de agua entran en el canal de CNT por iniciativa del movimiento browniano, mientras que dos lados de CNT compiten entre sí y se compensan. En nuestra investigación, una pequeña hoja que se mueve sobre la membrana debilita la competitividad de un lado e induce un flujo neto continuo. Durante las simulaciones, encontramos que el modo de movimiento de la hoja es la clave del rendimiento. El movimiento browniano puro induce un pequeño flujo de agua neto estable alrededor de 2 ns −1 eso es independiente de la temperatura de la hoja, mientras que el movimiento unidireccional puede crear un flujo significativamente mayor, dependiendo de la fuerza impulsora en la hoja. Además, con el aumento de la fuerza motriz, el tiempo de desplazamiento del agua se reduce linealmente, correspondiente al flujo de agua o al comportamiento del flujo. Demasiado, el movimiento unidireccional tiene un mayor impacto en la dinámica y termodinámica del agua. En consecuencia, presentamos creativamente haciendo uso de la permeabilidad del agua natural, lograda por una pequeña hoja de grafito colocada sobre la membrana, que sería útil para la tecnología RO.
Abreviaturas
- CNT:
-
Nanotubos de carbono
- MD:
-
Dinámica molecular
- RO:
-
Ósmosis inversa
Nanomateriales
- IoT y gestión del agua en el hogar
- Influencia del agua en la estructura y propiedades dieléctricas de la microcristalina y nanocelulosa
- Ajuste de las morfologías de la superficie y las propiedades de las películas de ZnO mediante el diseño de la capa interfacial
- Pros y contras de recubrir su bomba
- ¿Cuáles son los diferentes tipos de drenaje de aguas superficiales?
- La Bomba de Calor Perfecta Agua Caliente
- ¿Cuáles son las diferencias entre la bomba sumergible para acuarios y las bombas de aire en línea?
- Las cosas sorprendentes sobre las bombas sumergibles
- ¿Cómo elegir la mejor bomba de agua caliente sanitaria?
- Compresores de aire y secadores:la pareja perfecta
- Contaminación y la bomba hidráulica:descripción general



