Semicaticalidad libre de metales en sistemas gh-C3N4 dopados con B
Resumen
Media metalicidad que se eleva desde el s / p los electrones ha sido uno de los temas candentes de la espintrónica. Basándonos en los primeros principios de cálculo, exploramos las propiedades magnéticas del nitruro de carbono de heptazina grafítico dopado con B (gh-C 3 N 4 ) sistema. Se observa ferromagnetismo en el gh-C 3 dopado con B N 4 sistema. Curiosamente, su fase de estado fundamental (B C1 @ gh-C 3 N 4 ) presenta una fuerte propiedad de semi-metal. Además, la semimetalicidad en B C1 @ gh-C 3 N 4 Puede soportar hasta un 5% de deformación por compresión y un 1,5% de deformación por tracción. Sin embargo, perderá su semimetalicidad cuando la concentración de dopaje sea inferior al 6,25%. Nuestros resultados muestran que un sistema semimetálico libre de metales tiene aplicaciones espintrónicas prometedoras.
Antecedentes
Los dispositivos espintrónicos utilizan simultáneamente la libertad de carga y de espín de los electrones y han atraído cada vez más atención debido a su uso potencial en dispositivos lógicos y de memoria [1, 2]. Sin embargo, su rendimiento depende en gran medida de la relación de polarización de espín de las corrientes. Por lo tanto, existe una necesidad urgente de materiales que puedan generar corrientes con polarización de espín al 100%. Materiales semimetálicos, que pueden hacer esto en el nivel Fermi E F , se consideran los materiales ideales para los dispositivos espintrónicos [3, 4, 5, 6]. Muchos ferromagnetos semimetálicos, como las manganitas dopadas [7], las perovskitas dobles [8] y los compuestos de Heusler [9, 10], han atraído una gran atención en los últimos años. Sin embargo, estos materiales semimetálicos generalmente contienen metal de transición (TM) y tienen fuertes fuerzas de acoplamiento de giro-órbita, lo que da como resultado tiempos de relajación de giro cortos. Por lo tanto, es necesario desarrollar materiales semimetálicos avanzados sin TM con un tiempo de relajación de giro prolongado.
Los cristales atómicos bidimensionales (2D) con superficies planas han atraído mucha atención recientemente debido a su posible aplicación en dispositivos espintrónicos [11,12,13,14,15,16,17,18,19,20,21,22 , 23,24]. El grafeno y sus varios análogos 2D, como el nitruro de boro hexagonal y el nitruro de carbono, tienen un gran potencial para la espintrónica debido a sus propiedades excepcionales, por ejemplo, baja dimensionalidad y confinamiento de electrones. Aunque la mayoría de estos materiales son de naturaleza no magnética, hay muchas formas, como el dopaje y la deformación, de alcanzar el ferromagnetismo semimetálico. Por ejemplo, g-C 3 basado en trizaína incrustado en B, Al y Cu N 4 (gt-C 3 N 4 ) se ha informado que son semimetálicas [14]. El nitruro de carbono similar al grafeno también presenta semi-metalicidad bajo tensión de tracción [17]. Además, el g-C 3 basado en heptazina N 4 (gh-C 3 N 4 ) ha recibido muchas atenciones [25,26,27,28,29,30,31,32,33].
Un gran número de trabajos de investigación han investigado las propiedades electrónicas y magnéticas del gh-C incorporado en metales de transición 3 N 4 sistemas [11, 28, 30]. Estos gh-C 3 incrustados en metal de transición N 4 Los materiales se han sintetizado a temperatura elevada [34,35,36,37,38,39]. Los trabajos teóricos muestran que los metales de transición pueden unirse más fuertemente con gh-C 3 N 4 que con el grafeno y estos sistemas son metálicos [30]. Indrani y col. han investigado sistemáticamente las propiedades magnéticas de C-dope gh-C 3 N 4 sistemas mediante cálculos de la teoría funcional de la densidad (DFT) [40]. Descubrieron que todos estos C-dope gh-C 3 N 4 Los sistemas son ferromagnetismo, y una fase de alta energía muestra una fuerte semi-metalicidad y una temperatura de Curie de 400 K. Recientemente, Gao et al. [41] han demostrado experimentalmente la capacidad de fabricar gh-C 3 dopado con B N 4 nanohojas, que presentan ferromagnetismo y semimetalicidad a alta temperatura. A pesar de estos primeros trabajos, una investigación teórica sistemática del gh-C 3 dopado con B N 4 Está perdido. Algunas cuestiones fundamentales, como los efectos de la posición de dopaje y la concentración de B sobre las propiedades electrónicas y magnéticas de gh-C 3 N 4 aguardar una aclaración. Además, también es necesario investigar los efectos de la tensión.
En este trabajo, investigamos sistemáticamente los efectos de las posiciones de dopaje, las concentraciones de B y la tensión sobre las propiedades electrónicas y magnéticas del gh-C 3 dopado con B N 4 sistema a través de cálculos de primeros principios. Los resultados muestran que se puede encontrar una fuerte semi-metalicidad en el estado fundamental de gh-C 3 dopado con B N 4 (B C1 @ gh-C 3 N 4 ). No solo las posiciones de dopaje, sino también las concentraciones de dopaje, juegan un papel importante en la inducción de la metalicidad a medias. Además, la semimetalicidad en B C1 @ gh-C 3 N 4 Puede soportar hasta un 5% de deformación por compresión y un 1,5% de deformación por tracción. El gh-C dopado B 3 N 4 Los sistemas son prometedores para la espintrónica, por lo tanto.
Métodos de cálculo
Un tetragonal de 28 a.u. celda que contiene dos celdas primitivas de gh-C 3 N 4 como se muestra en la Fig.1 se ha empleado para simular el gh-C 3 dopado con B N 4 sistema. La relajación de la estructura geométrica y el cálculo de la estructura electrónica estática se realizan utilizando el paquete VASP [42, 43], que se basa en la teoría funcional de la densidad (DFT). Se utiliza la aproximación de gradiente generalizado (GGA) de Perdew-Burke-Ernzerhof (PBE) [44] y los potenciales de onda aumentada del proyector (PAW). La energía de corte se establece en 500 eV y se elige una cuadrícula de puntos k Monkhorst-Pack de 1 × 9 × 15 para lograr un equilibrio entre el tiempo de cálculo y la precisión. Todas las estructuras geométricas están completamente relajadas. El umbral de convergencia se establece en 10 −6 eV en pasos electrónicos y 5 × 10 −3 eV / Å en vigor. Para evitar la interacción entre dos imágenes periódicas adyacentes, la región de vacío a lo largo de la x -la dirección se establece en 15 Å. Para investigar los efectos de las concentraciones de dopaje, se adoptó una supercélula tetragonal 112-atómica compuesta de 2 × 2 × 1 celdas unitarias tetragonales y una cuadrícula de puntos k Monkhorst-Pack de 1 × 5 × 9.
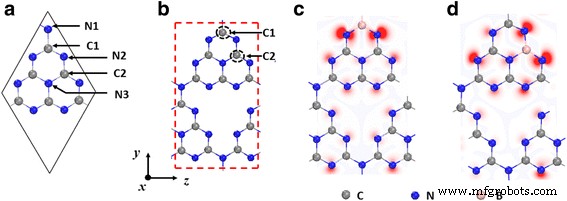
un Representación esquemática de prístina gh-C 3 N 4 . Hay dos átomos de C no equivalentes (C1 y C2) y tres átomos de N no equivalentes (N1, N2 y N3). b El tetragonal 28 a.u. celda de gh-C 3 N 4 se utiliza aquí para simular el gh-C 3 dopado con B N 4 sistema (correspondiente a una concentración de dopaje del 8,33%). Los círculos de trazos negros indican los posibles sitios de dopaje B. c , d Las estructuras optimizadas de B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 , respectivamente. Distribuciones de la densidad de carga del estado de giro menos el estado de giro hacia abajo para B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 también se muestran aquí. Los colores rojo y azul etiquetan las cargas de aceleración y desaceleración, respectivamente
Resultados y discusiones
En un gh-C puro 3 N 4 sistema, hay dos átomos de C no equivalentes (C1 y C2) y tres átomos de N no equivalentes (N1, N2 y N3) como se muestra en la figura 1a. Encontramos los parámetros de celosía relajada ( a = b =7.14 Å) del gh-C puro 3 N 4 concuerda bien con los informes experimentales y teóricos anteriores [40, 45]. La estructura de la banda y la correspondiente densidad total de estados (DOS) de gh-C 3 N 4 se muestran en la Fig. 2a. Para comprender mejor las propiedades electrónicas del gh-C 3 N 4 , las distribuciones de carga de las bandas de borde C 1 , V 1 , y la correspondiente densidad local de estados se presentan en la Fig. 2b, c. Puede verse claramente que la parte inferior de la banda de conducción C 1 está dominado por el π * estados de los átomos C1, C2 y N3, que se originan en el p x orbitales. Sin embargo, la parte superior de la banda de valencia V 1 está determinada por los estados δ no enlazantes de los átomos de N2 y los estados π de los átomos de N3.
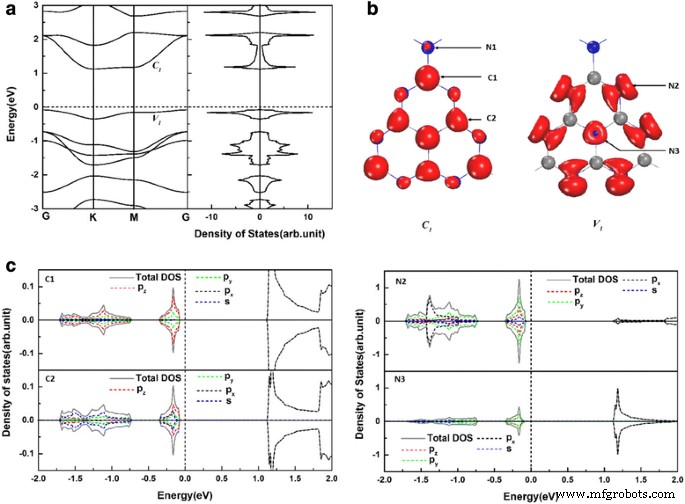
un Las estructuras de bandas electrónicas y la densidad total de estados de prístina gh-C 3 N 4 . b Las distribuciones de carga de las bandas de borde C 1 y V 1 (indexado en a ). c La densidad de electrones resuelta en órbita de los estados proyectados en el átomo C1, el átomo C2, el átomo N2 y el átomo N3 (indexados en b ). La energía en el nivel de Fermi se establece en cero
Una celda unitaria tetragonal que contiene 28 átomos de gh-C 3 N 4 (correspondiente a una concentración de dopaje del 8,333%) se emplea para simular el gh-C 3 dopado con B N 4 sistema como se muestra en la Fig. 1b (la línea roja discontinua). Después de considerar el informe inicial [31] de que la sustitución en los sitios C (C1 y C2) es más favorable que en los sitios N (N1, N2 y N3), solo se han investigado las configuraciones de B que sustituyen a C para explorar sus propiedades magnéticas. propiedades. Como resultado, los dos gh-C 3 diferentes dopados con B N 4 isómeros (B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 ) se estudian. Las estructuras completamente relajadas de B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 se dan en la Fig. 1c, d, respectivamente.
La estabilidad estructural depende del grado de cohesión y el sistema con energía cohesiva absoluta negativa y grande tiene una mejor estabilidad. Las energías cohesivas ( E coh ) de B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 se han calculado utilizando
$$ {E} _ {\ mathrm {coh}} =\ left [{E} _ {\ mathrm {tot}} - \ sum {M} _i {E} _i \ right] / M \ left (i =\ mathrm {C}, \ mathrm {N}, \ mathrm {B} \ right) $$donde E tot es la energía total de un gh-C dopado con B 3 N 4 sistema y E i es la energía de un átomo aislado para el elemento i en la misma celda. La M i y M son el número de i th especie y el número total de átomos presentados en el gh-C dopado B 3 N 4 sistema, respectivamente. Encontramos que las energías cohesivas son - 6,107 y - 6,097 eV por átomo para B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 , respectivamente. Por lo tanto, el B C1 @ gh-C 3 N 4 fase es energéticamente favorable. Esta conclusión concuerda bien con el trabajo anterior [31]. Para estudiar más a fondo la estabilidad relativa de los dos gh-C 3 dopados con B N 4 sistemas, las energías cohesivas de 2D C 2 N y gh-C 3 N 4 , que han sido sintetizados experimentalmente, se calculan y son iguales a - 6,813 y - 6,091 eV por átomo, respectivamente. Curiosamente, tanto B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 tienen energías cohesivas intermedias entre C 2 N y gh-C 3 N 4 . En consecuencia, deben tener una estabilidad estructural y mecánica intermedia.
Para determinar la viabilidad termodinámica y el costo energético relativo de B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 en comparación con sus prístinos análogos 2D, las energías de formación también se han calculado utilizando
$$ {E} _f =\ left \ lfloor {E} _ {\ mathrm {tot}} - \ sum {M} _i {\ mu} _i \ right \ rfloor / M \ left (i =\ mathrm {C} , \ mathrm {N}, \ mathrm {B} \ right) $$donde E tot , M i y M son los mismos que los del cálculo de la energía cohesiva. μ i es el potencial químico del i th especie. Aquí, el grafeno, el boro romboédrico y el nitrógeno gaseoso se utilizan para determinar los potenciales químicos μ C , μ B y μ N , respectivamente. Las energías de formación calculadas son 0,222 y 0,232 eV por átomo para B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 , respectivamente. Como comparación, la energía de formación de gh-C 3 N 4 es 0,293 eV por átomo. Además, el E calculado f valores de B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 son ligeramente inferiores a gh-C 3 N 4 , indicando estos gh-C 3 dopados con B N 4 se pueden fabricar isómeros. De hecho, la síntesis de gh-C 3 dopado con B N 4 se ha informado [41].
Para conocer los estados de tierra magnéticos de B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 , hemos investigado los estados no polarizado de espín (NSP), ferromagnético (FM) y antiferromagnético (AFM). Los resultados muestran que el estado FM es el estado fundamental para los dos gh-C 3 dopados con B N 4 sistemas, y sus momentos magnéticos son ambos 1.0 μ B por celda unitaria como se muestra en la Tabla 1. Para una mayor comprensión del magnetismo de los dos gh-C 3 dopados con B N 4 sistemas, las densidades de carga dependientes del espín de B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 han sido investigados y representados en las Fig. 1c, d, respectivamente. Ligeramente diferente del gh-C 3 dopado con C N 4 sistemas en los que la densidad de giro se encuentra principalmente en los sitios C dopados [40], la densidad de giro de gh-C dopado B 3 N 4 se localiza principalmente en los átomos de N2 coordinados 2 veces, especialmente los átomos de N2 adyacentes a los átomos dopantes B, como se muestra en la Fig. 1c, d. Debido a que el dopante B tiene un electrón menos que el átomo de C sustituido, se induce un defecto π en gh-C 3 dopado con B N 4 sistema, lo que resulta en 1.0 μ B momento magnético.
Para comprender los efectos del dopaje B en el gh-C 3 N 4 sistemas, realizamos la estructura de banda polarizada de espín y los cálculos de densidad de estados para B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 , como se muestra en la Fig. 3a, d, respectivamente. Los resultados muestran que la asimetría entre las densidades de giro hacia arriba y hacia abajo en B C1 @ gh-C 3 N 4 y B C2 @ gh-C 3 N 4 induce un magnetismo evidente. Curiosamente, como se muestra en la Fig. 3a, encontramos que el B C1 @ gh-C 3 N 4 Los sistemas tienen una propiedad semimetálica ya que uno de los canales de giro es metálico, mientras que el otro es aislante. Las gráficas de estructura de bandas y densidad total de estados muestran que la división de espín ocurre cerca del nivel de Fermi y dos bandas de giro hacia abajo están cruzando el nivel de Fermi, mientras que las de giro hacia arriba tienen una banda prohibida de 1.23 eV. Esto se debe principalmente a los grandes vacíos presentes en el gh-C 3 N 4 marco, que conducen a la localización de estados electrónicos. La banda prohibida en el canal giratorio de B C1 @ gh-C 3 N 4 es mucho más grande que los espacios (en uno de los canales de giro) de manganitas dopadas [7], perovskitas dobles [8], compuestos de Heusler [9, 10] y nanocintas de grafeno [46]. La fuerza semimetálica del B C1 @ gh-C 3 N 4 Los sistemas pueden ser comparables con el gh-C 3 dopado con C N 4 [40]. Un sistema semimetálico tan fuerte es muy prometedor porque no es posible la transición spin-flip de los portadores de la excitación térmica. Para explorar más a fondo los orígenes de la semi-metalicidad en B C1 @ gh-C 3 N 4 , las distribuciones de carga de las dos bandas de spin-down que atraviesan el nivel de Fermi se presentan en la Fig. 3b. Vemos claramente que la semimetalicidad de B C1 @ gh-C 3 N 4 proviene principalmente de los estados δ no enlazantes de los átomos de N2. La densidad local de estados (ver Fig. 3c) también muestra que la semimetalicidad de B C1 @ gh-C 3 N 4 se origina principalmente en el p z órbitas de átomos de N2 junto con una contribución parcial de la p z órbitas de los átomos B y N1. Están de acuerdo con los informes anteriores sobre gt-C 4 N 3 [2], donde los orbitales N proporcionan una contribución importante a la semimetalicidad. Para el B C2 @ gh-C 3 N 4 , las gráficas de estructura de bandas y densidad total de estados (Fig. 3a) también muestran que la división de espín ocurre cerca del nivel de Fermi. El estado de mayoría de spin tiene una banda prohibida de 1,36 eV. Sin embargo, el estado de minoría de espín muestra una banda prohibida de 0,016 eV. Las distribuciones de carga de las bandas de borde y la densidad local de los estados para B C2 @ gh-C 3 N 4 muestran que tanto los bordes de la banda de valencia como los bordes de la banda de conducción de B C2 @ gh-C 3 N 4 están dominados por los estados δ no vinculantes, que se originan principalmente en el p y y p z orbitales de átomos de N2. Esto significa que los estados δ no enlazantes de los átomos de N2 se dividen cuando un átomo de B sustituye a un átomo de C en gh-C 3 N 4 sistema y determinar sus propiedades electrónicas.
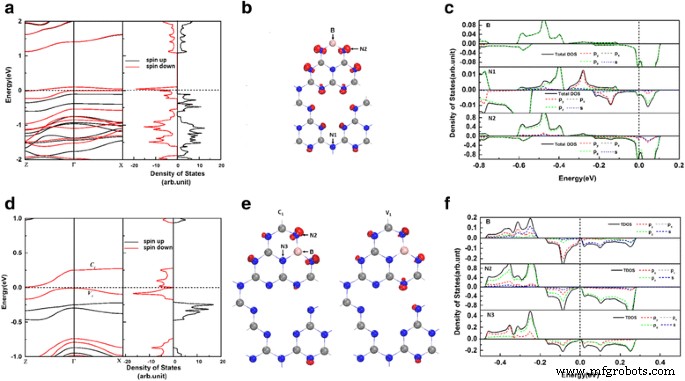
un La estructura de bandas dependiente del espín y la densidad total de estados de B C1 @ gh-C 3 N 4 . b Las densidades de carga de las dos bandas que cruzan el nivel de Fermi. c La densidad de electrones resuelta en orbital de los estados proyectados en el átomo B, el átomo N1 y el átomo N2 (indexados en b ) para B C1 @ gh-C 3 N 4 . d - f son iguales con a - c pero para B C2 @ gh-C 3 N 4 . La energía en el nivel de Fermi se establece en cero
Para aclarar la dependencia de la semimetalicidad en el B C1 @ gh-C 3 N 4 sistemas sobre concentraciones de dopaje, se ha empleado una supercélula tetragonal 112-atómica de celda unitaria tetragonal de 2 × 2 × 1 y se investigan tres concentraciones de dopaje B diferentes (2.083, 4.167 y 6.25%), como se muestra en la Fig. 4a, b . Como podemos ver en la Fig. 4b, B C1 @ gh-C 3 N 4 todavía puede mantener la semimetalicidad para una concentración de dopaje del 6,25%. Sin embargo, pierde su semimetalicidad cuando la concentración de dopaje es igual o inferior al 4,167%.
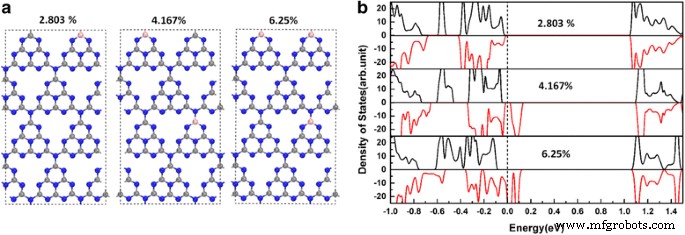
un Representaciones esquemáticas de la supercélula tetragonal 112-atómica utilizada para simular diferentes concentraciones de dopaje de B C1 @ gh-C 3 N 4. b La densidad total dependiente del espín de los estados de B C1 @ gh-C 3 N 4 con diferentes concentraciones de dopaje. La energía en el nivel de Fermi se establece en cero
La tecnología de deformación se usa comúnmente para ajustar las propiedades de giro de un material magnético, y se debe estudiar el efecto de deformación sobre la metalicidad media de un material. Aquí, llevamos a cabo los cálculos de densidad de estado para el B C1 @ gh-C 3 N 4 sistema bajo la tensión biaxial in-plain. Se encuentra que la resistencia a la semimetalicidad disminuye gradualmente a medida que aumenta la deformación por tracción biaxial. Pierde la mitad de la metalicidad cuando la deformación por tracción biaxial alcanza el 1,5%, como se muestra en el panel de la Fig. 5. Sin embargo, mantiene la mitad de la metalicidad hasta el 5% de la deformación por compresión biaxial (ver el panel derecho de la Fig. 5). Por lo tanto, este sistema se comporta bien bajo tensión externa.
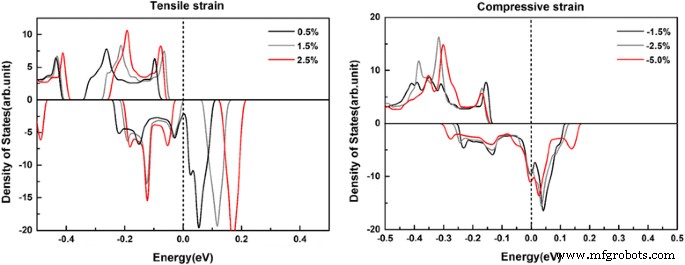
La densidad total dependiente del espín de los estados de B C1 @ gh-C 3 N 4 (con una concentración de dopaje del 8,33%) bajo tensión de tracción biaxial en plano (izquierda) y tensión de compresión biaxial (derecha), respectivamente. La energía en el nivel de Fermi se establece en cero
Conclusión
Basado en cálculos de la teoría funcional de densidad, el gh-C 3 dopado con B N 4 Se han investigado sistemas para posibles aplicaciones en dispositivos espintrónicos. Se observa ferromagnetismo en todos los gh-C 3 dopados con B N 4 sistemas. Además, una fuerte semi-metalicidad se logra solo en la fase de estado fundamental, es decir, B C1 @ gh-C 3 N 4 , que resulta de una división de espín de los estados δ no enlazantes de átomos de N2 coordinados 2 veces altamente insaturados. La semimetalicidad se pierde con concentraciones bajas de dopaje B. Por tanto, tanto el dopaje selectivo como su concentración juegan un papel importante en la inducción del magnetismo y la semimetalicidad. La semi-metalicidad en B C1 @ gh-C 3 N 4 Puede soportar hasta un 5% de deformación por compresión y un 1,5% de deformación por tracción. Estos resultados muestran que el gh-C dopado con B 3 N 4 Los sistemas podrían ser un material semimetálico ferromagnético para memoria magnética y dispositivos espintrónicos.
Nanomateriales
- Sistemas de numeración
- Sistemas de señales de voltaje
- Sistemas de señales actuales
- Sistemas de energía monofásicos
- Modernización de la ciberseguridad
- ¿Cómo funcionan los sistemas SCADA?
- ¿Qué es la seguridad de IoT?
- Sistemas SCADA e industria 4.0
- Construcción de sistemas hidráulicos
- Introducción a los sistemas de corte de perfiles
- Selección de un integrador de sistemas



