Tratamiento de campo electromagnético de RF de absorbentes de luz CZTSSe de kesterita tetragonal

Resultados y discusión

Como prueba de un principio, comenzamos a estudiar la influencia de los FR en el tratamiento de las CS. Los resultados recopilados se presentan en la Fig. 1.

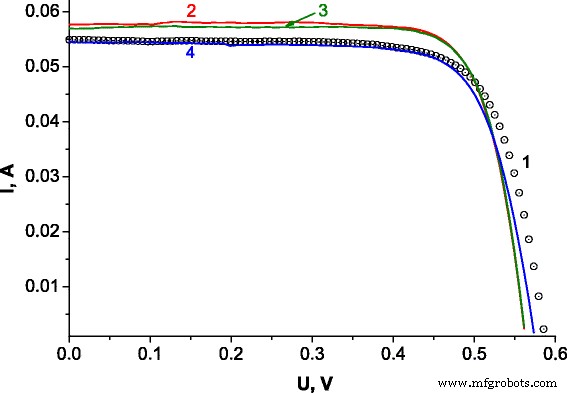
Características de AM1.5 UI de SC basados ​​en Si en configuración general bajo tratamientos de RF (descarga estimulada de 13.56 MHz H ⁺ plasma, t =15 min, P =0,8 W / cm ² ) con los siguientes valores de intensidad: 1 inicial, 2 95 W, 3 225 W, 3 225 W y 4 300 W

Eficiencia ( η ,%) y factor de llenado (FF) de Si-SCs fueron 11,692 y 0,746 (curva 1), respectivamente, y mejoraron después de los tratamientos:95 W =12,337 / 0,775 (curva 2); 225 W =12,291 / 0,783 (curva 3); 300 W =11,458 / 0,752 (curva 4). Las pendientes de las curvas 2 y 3 difieren ligeramente de las correspondientes a la muestra inicial (curva 1). Suponemos que esto es el resultado de la degradación de los contactos Schottky debido al calentamiento que ocurre bajo RF. Como puede verse en la Fig.1, los valores de U _oc disminuyó pero los valores de I _sc aumentado. Esto puede suceder posiblemente debido a la pasivación de enlaces colgantes por átomos de H altamente reactivos. La aplicación de un tratamiento de RF de alta potencia resultó en el agrietamiento de los contactos metálicos rayados y la destrucción de la unión p-n. Esto se observó en microscopio óptico, explicando el comportamiento de la curva 4 y su cambio significativo. Por lo tanto, asumimos que el método propuesto se puede aplicar para la modificación de η y FF, pero debería optimizarse para mejorar TFSC.

Para la caracterización de la muestra, se procedió a las medidas de los espectros de reflectividad. Generalmente, el coeficiente de absorción se puede extraer fácilmente de las mediciones de transmisión. Sin embargo, existen dificultades tanto en la medición precisa del espesor como en las pérdidas de reflectividad en el caso de una configuración multicapa del absorbente, o si su espesor apropiado es inferior a 1 µm. Por estas razones, es muy conveniente realizar el segundo método independiente para medir el coeficiente de absorción a partir de las mediciones de la reflectividad. El coeficiente de absorción está relacionado con el coeficiente de extinción por una relación simple: α ( ω , E ) =4 πk ( ω ) λ ^{- 1} =2 ωk ( ω ) c ^{- 1} =2 E ( ℏc ) ^{- 1} k ( E ), [ α ( ω , E )] = cm ^{- 1} , donde k ( ω, E ) es el coeficiente de extinción, ω es la frecuencia angular, λ es la longitud de onda, c es la velocidad de la luz y ℏ es la constante de Planck reducida, respectivamente. La amplitud de reflexión compleja se puede escribir utilizando ecuaciones de Fresnel y, en el caso de una incidencia normal, se lee

donde n ₀ es el índice de refracción de los medios para un haz incidente ( n ₀ ≥ 1), y la refracción del material se caracteriza por el índice de refracción complejo n = n ₁ + ik . Mientras r es una reflectividad compleja y no se mide por sí misma, se puede descomponer fácilmente como cualquier número complejo utilizando la fórmula de Euler:

donde R es la relación de las intensidades de los haces de luz reflejados e incidentes que se pueden medir directamente, θ es la fase de la luz reflejada, A y B son los componentes reales e imaginarios de la reflectividad compleja, y n ₁ y k son los índices de refracción y extinción del absorbedor, respectivamente.

Eq. (1) se puede reescribir mediante descomposición directa en partes reales e imaginarias como

Si conocemos R y θ son transformados por el algoritmo utilizado en las Refs. [11, 12], la solución del sistema de Eq. (2) da

donde los coeficientes auxiliares son

En la región donde las fuerzas del oscilador para las transiciones ópticas se agotan en su mayoría, la función dieléctrica se puede representar mediante la fórmula clásica de Drude [13, 14]:

donde σ ( ω ) es la conductividad óptica compleja (índices en minúsculas r y im denotar parte real e imaginaria, respectivamente), ω _p es la frecuencia plasmática de los electrones de valencia, m * es la masa de electrones libres, N _v es la densidad efectiva de los electrones de valencia, τ es el tiempo medio de colisión y ε ₀ es la permitividad del vacío, respectivamente. Todos estos parámetros deben atribuirse al valor de la frecuencia del plasma mediante la regla de la suma:\ (\ frac {1} {2} \ pi {\ omega_p} ^ 2 ={\ displaystyle \ underset {0} {\ overset {\ infty } {\ int}} \ frac {\ omega {\ varepsilon} _ {im}} {\ varepsilon_r ^ 2 + {\ varepsilon} _ {im} ^ 2} d \ omega}. \)

Espectros ópticos transformados de R (E) _initial / R (E) _RF de CZTSSe correspondientes a diferentes condiciones tecnológicas se muestran en la Fig. 2a. El análisis mostró que la reflexión de las estructuras después del tratamiento con RF disminuyó en el rango de frecuencia de 1.2 a 3 eV en el caso de estructuras multicapa (curvas 2 y 3) y en el rango de 2.4 a 3.3 eV (curva 1) para estructuras a granel. El desajuste de los rangos de mejora se produce debido a la muestra libre posprocesada a granel (curva 1) y la presencia de contactos Schottky o heterouniones para la muestra en capas (curvas 2 y 3). Cabe señalar que la transformación de espectros siguiendo el procedimiento de la Ref. [15] no sería correcto sin términos de corrección dependiendo de la configuración de medición de los haces. En el caso de la configuración A, los cambios de configuración ATR del período de ángulo de fase complejo influyen en la determinación del índice de refracción complejo y deben corregirse. Usando una técnica que no es ATR, el cambio de fase real θ _actuar se puede obtener de forma similar al procedimiento descrito en la Ref. [15]. En nuestros experimentos, la mejor predicción del índice de refracción se realizó para la configuración D, ligeramente peor para B _s configuración, y difícil de configurar. Esto depende de las transiciones durante los reflejos múltiples de los espejos. Se descubrió que era imposible realizar una estimación adecuada del ángulo de fase en la configuración C debido a la esfera de integración difusa. Por lo tanto, llegamos a la conclusión de que la determinación del coeficiente de absorción, así como de las funciones pseudoópticas a partir de las mediciones de reflectividad, es correcta para la medición de la reflexión especular absoluta de un solo haz de incidencia normal. De lo contrario, todos los resultados deben atribuirse a los parámetros obtenidos por el método directo (p. Ej., Técnica basada en ángulos de Brewster).

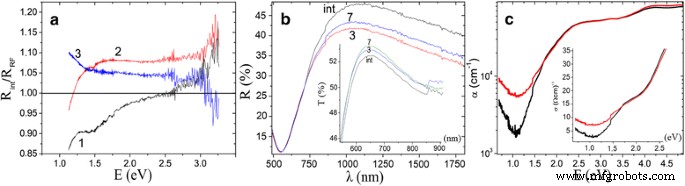
Espectros ópticos de CZTSSe antes y después de los tratamientos de RF. un 1 Relación de reflectancias para CZTS a granel procesado a partir de precursores metálicos (configuración A); 2 relación de reflectancias para vidrio / Mo / Cu / CZTSe (configuración A); 3 reflectancia de CZTS a granel procesado a partir de precursores de sulfuro (B _d configuración). b Reflectancia y transmitancia ( insertar ) de CZTS con respecto a la exposición al plasma (configuración C) con los pasos 1, 3 y 7. c Espectros de absorbancia de películas delgadas de CZTS con ( negro ) y sin ( rojo ) Tratamiento de RF durante 3 min (configuración C). Insertar :espectros de conductividad óptica de las mismas películas

La siguiente etapa de experimentos incluyó mediciones de transmisión y reflexión de las películas sobre el vidrio con dimensiones laterales mayores que la apertura típica de los haces de espectrofotómetros de doble haz. Para ello, el CZTS a granel se evaporó mediante haz de electrones y luego se trató adicionalmente con plasma de RF. El paso para la exposición fue de 1 min. Los respectivos espectros de reflectancia y transmitancia (inserto) se ilustran en la Fig. 2b, de acuerdo con la relación de exposición. Se ha revelado el efecto máximo para el tiempo de exposición de la muestra de 3 min (curva 3).

Después de eso, los coeficientes de absorción correspondientes y las relaciones entre las conductividades ópticas iniciales se calcularon mediante las Ecs. (3) y (6) utilizando el resultado obtenido por el método más eficaz. Se ilustran en la Fig. 2c y en el recuadro de esta figura, respectivamente.

Se puede realizar una estimación por mínimos cuadrados de parámetros no lineales minimizando el procedimiento utilizando las siguientes relaciones:

$$ \ left \ {\ begin {array} {l} T =\ frac {{\ left (1- R \ right)} ^ 2} {e ^ {\ alpha d} - {R} ^ 2 {e} ^ {- \ alpha d}}; \\ {} R =1- \ frac {4 {n} _0 {n} _1} {{\ left ({n} _0 + {n} _1 \ right)} ^ 2+ {k} ^ 2}; \\ {} k =\ frac {\ alpha \ left (\ lambda, E \ right)} {4 \ pi \ lambda}. \ end {array} \ right. $$ (7)

Aquí, la primera relación se conoce como ley de Beer en el caso de reflejos múltiples en placas paralelas y la segunda es el cuadrado del valor absoluto de la reflectividad compleja.

Como puede verse en la Fig. 2c, las propiedades de absorción de luz de CZTS aumentaron después del tratamiento con RF principalmente dentro de la banda prohibida. El valor de la conductividad óptica puede evaluarse utilizando el supuesto del modelo de conductividad de Drude, así como el parámetro de frecuencia de plasma correspondiente a los tratamientos. En el caso del tratamiento con RF, su valor es de 2,294 eV, que es ligeramente superior al del caso inicial (2,278 eV). Con base en estos resultados, asumimos que el tratamiento con RF mejora la absorción. Pero la presencia de componentes ricos en Cu y otros componentes enriquecidos con metales da como resultado propiedades electrónicas deficientes, y la condición del tratamiento debe optimizarse mediante una limpieza adicional.

Para estimar el papel de los componentes plasmáticos durante el tratamiento, se aplicó la técnica FTIR. Los espectros de absorción se presentan en la Fig. 3. Bandas de absorción para CZTS ₄ a granel con y sin tratamiento de RF osciló entre 500 y 4000 cm ⁻¹ (números de olas). Estas bandas incluyen C – N (1250 cm ⁻¹ , 1600 cm ⁻¹ ); sp ² enlaces hibridados (1490-1650 cm ⁻¹ ) de C – C, C =C bandas de estiramiento; banda de estiramiento de CH _n a 2870 y 3100 cm ⁻¹ , correspondiente a sp ⁿ enlaces hibridados; CO ₂ (2350 cm ⁻¹ ); y 2700 y 3600 cm ⁻¹ atribuido al agua y componentes orgánicos [16]. Como podemos ver, el tratamiento de RF resultó en la reducción de la absorción en todo el rango espectral. En el caso de absorción por sp ² enlaces hibridados para unidades C – C y C =C a 1500-1650 cm ⁻¹ , la explicación es bien conocida. Normalmente, las fases similares al grafito están expuestas a H ⁺ el plasma se extrae de las estructuras [16]. La disminución de la intensidad de la banda de absorción relacionada con las oscilaciones simétricas de CH ₃ enlace (a 2872 cm ⁻¹ ), CH y CH ₂ (2900–2926 cm ⁻¹ ) puede explicarse por la reducción de la concentración de hidrógeno en la película. Por tanto, H ⁺ Los iones eliminan los componentes de las impurezas debido a su alta movilidad incluso si la muestra está enmascarada sin acumulación de sp ⁿ composiciones hibridadas.

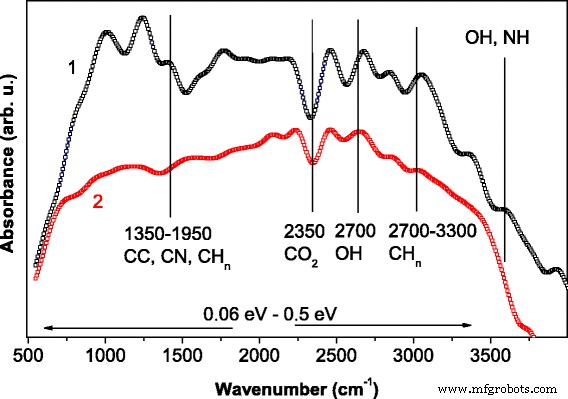
Espectros FTIR de muestra de CZTS a granel con (curva 1) y sin (curva 2) tratamiento de RF (descarga estimulada de 13,56 MHz H ⁺ plasma, t =15 min, P =0,8 W / cm ² )

Los espectros Raman del CZTS a granel se deconvolucionaron en componentes de Lorentz y se presentan en la Fig. 4. Los dos picos dominantes a 286 y 335 cm ⁻¹ y las bandas a 251, 305, 343 y 356 cm ⁻¹ se atribuyeron a los modos de simetría A, E y B, respectivamente. Sus posiciones eran similares a las de los resultados experimentales descritos en las Refs. [17,18,19], y su asignación de simetría fue consistente con los cálculos teóricos reportados en las Refs. [20, 21]. Ajustando el espectro Raman por un conjunto de componentes, podemos suponer que un componente más débil alrededor de 329 cm ⁻¹ se observa en el lado de baja frecuencia para la banda más intensa (335 cm ⁻¹ ). Esta banda Raman se puede asignar al desorden de átomos de Zn y Cu en la red CZTS como se discutió en la Ref. [22]. Este desorden a menudo es causado por los llamados defectos anti-sitio, como los átomos de Zn que reemplazan al Cu (Cu _Zn ) y viceversa (Zn _Cu ). La influencia de la fase en el cambio de los espectros Raman para la kesterita se analiza en la Ref. [22]. El grado de desorden de la estructura de la kesterita se puede estimar usando la relación de intensidad I ₃₂₉ / I ₃₃₅ de los picos a 329 y 335 cm ⁻¹ . En nuestro caso, esta relación fue de 0,11 y es comparable a los valores obtenidos para películas delgadas descritos en [22]. Cabe señalar que los cambios en los espectros Raman para las áreas claras y oscuras son insignificantemente pequeños que se correlacionan con la Ref. [23].

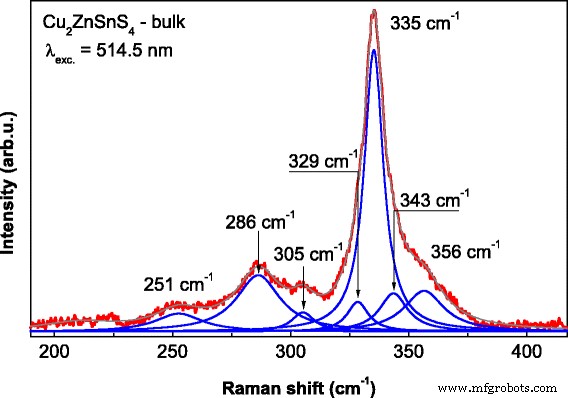
Espectro Raman de muestra de CZTS a granel con ajustes de Lorentzian ( I ~ 0,5 mW; λ =514,5 nm)

Espectros Raman de CZTS y Cu ₂ ZnSnSe ₄ (CZTSe) muestras después de tratamientos de RF se muestran en la Fig. 5a, b respectivamente. Están marcados en azul y rojo correspondientes a las muestras iniciales y tratadas con RF, respectivamente. Como puede verse en la Fig. 5a (línea roja), la posición de la banda a 286 cm ⁻¹ se desplaza a la región de alta frecuencia en 2 cm ⁻¹ , y su ancho medio se reduce casi dos veces (22 cm ⁻¹ ), resultando en el aumento de intensidad de la banda. En Ref. [24], Suragg y col. sugirió una hipótesis de que el I ₂₈₆ / I ₃₀₅ La relación se puede utilizar para determinar el orden de los compuestos. El compuesto uniforme se caracteriza por el valor de relación más alto y viceversa. Aplicando este supuesto, la intensidad del aumento de la banda de la relación I ₂₈₈ / I ₃₀₅ y su correlación con nuestros resultados (la disminución de la relación I ₃₃₁ / I ₃₃₇ ) fue establecido. Ambos valores indican el orden de la estructura del compuesto. Como puede verse, la banda más intensa a 335 cm ⁻¹ para A simetría se desplaza 2 cm ⁻¹ después del tratamiento, pero su ancho medio permanece igual a 10 cm ⁻¹ correspondiente al de la muestra sin tratar. Suponemos que todas las mejoras aparecieron debido al pedido de la red cristalina de kesterita. La kesterita desordenada tiene una estructura como la estanita y se manifiesta en el espectro como una banda a 331 cm ⁻¹ [23]. Nuestra suposición se basa en la disminución de la relación I ₃₃₁ / I ₃₃₇ igual a 0,06 [22]. En el recuadro de la Fig. 5a, demostramos tres curvas y mostramos que los cambios inducidos por RF son estables en el tiempo de todos modos dentro de un período de 1 mes, como lo indica la estabilidad de las posiciones de la banda principal. Al mismo tiempo, la banda a 370 cm ⁻¹ corresponde a CZTS y es visible después de que el tratamiento desapareció durante este período. El aumento de la intensidad de la banda a 370 cm ⁻¹ con respecto al de las muestras iniciales se asoció con el tratamiento de RF, ya que después de 1 mes de almacenamiento en aire la intensidad de la banda ha disminuido.

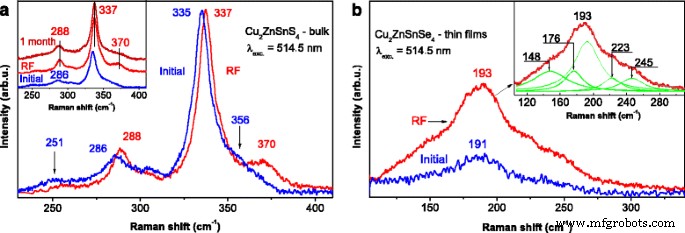
Espectros Raman de muestras a granel antes ( curvas azules ) y después ( curvas rojas ) Tratamiento de RF para materiales. un CZTS ( recuadro muestra los espectros antes, inmediatamente después y 1 mes después del tratamiento con RF). b Película CZTSe depositada sobre vidrio recubierto de Cu / Mo ( recuadro muestra la deconvolución por ajustes de Lorentzian)

Se proporcionó un tratamiento similar al CZTSe procesado en una configuración de múltiples capas, y sus espectros deconvolucionados se muestran en la Fig. 5b. El espectro se caracteriza por la presencia de dos picos principales a 193 y 176 cm ⁻¹ identificadas como las resonancias principales en CZTSe [25], así como picos específicos de CZTSe más débiles ubicados en 223 y 245 cm ⁻¹ . La banda de frecuencia de 223 cm ⁻¹ corresponde a la oscilación de la estructura similar a la kesterita de simetría E de CZTSe, una banda con una frecuencia de 245 cm ⁻¹ que corresponde a la simetría B de la estructura similar a la kesterita [21, 26]. A diferencia de CZTSSe, no hay características espectrales distintas que puedan asociarse con condiciones tecnológicas. Posiciones de fase secundaria principalmente para ZnSe y Cu ₂ SnSe ₃ difieren de los discutidos en la Ref. [25,26,27], en nuestro caso sin ninguna segunda fase significativa. En este caso, la evaporación por haz de electrones de las muestras a granel se realizó sobre un sustrato bajo calentamiento hasta 190 ° C [28] sin recocido adicional para alcanzar la estequiometría. Las condiciones dependieron del uso de sustrato orgánico durante el procesamiento posterior. Sin embargo, el tratamiento con RF también resultó en un efecto positivo para el espectro de CZTSe cuya banda principal se desplazó 2 cm ⁻¹ desde 191 cm ⁻¹ (curva azul) a 193 cm ⁻¹ (curva roja). Esto da razones para asumir que la influencia del tratamiento tiene un efecto similar para ambos materiales y está asociado con la reducción parcial de defectos estructurales.

Conclusiones

En este trabajo, aplicamos descargas de plasma de potencia débil a base de hidrógeno utilizando un tratamiento de campo electromagnético de radiofrecuencia (13,56 MHz) para mejorar las propiedades ópticas de muestras de kesterita a granel y de película fina. Las características estructurales y las propiedades ópticas fueron estudiadas por Raman, FTIR y espectroscopia de reflexión de incidencia normal. Se demostró que la posición de la banda principal de kesterita (286 y 335 cm ⁻¹ para CZTS) cambiado a la región de alta frecuencia en 2 cm ⁻¹ y su ancho completo a la mitad del máximo disminuyó casi dos veces (para los 286 cm ⁻¹ modo). Esto da como resultado un aumento de la intensidad de la banda. Desplazamiento similar de 2 cm ⁻¹ con respecto a la banda principal de simetría A apareció en la dispersión Raman de películas delgadas CZTSe. El análisis mostró que las mejoras resultaron del orden de la red cristalina y se mantuvieron estables durante un período de 1 mes. La espectroscopia FTIR mostró que los tratamientos con muestras eliminaron las impurezas a base de carbono e inhibieron la acumulación de sp ⁿ Composiciones hibridadas. Los espectros de reflexión se transformaron en espectros de absorción utilizando las integrales de dispersión en el rango espectral visible. Esto permitió estimar la función pseudoóptica, la conductividad Drude y el cambio de movilidad del portador, así como la concentración antes y después de los tratamientos con plasma. Therefore, plasma treatment resulted in not only surface cleaning from organic inclusions but also relieved internal stress. Such processing can be performed inside vacuum chambers during the post-processing stage. We conclude therefore that proposed hydrazine-free method of treatment can be applied for the creation of light absorbers with reduced strain and is suitable for the production of thin film multilayered solar cell.

Abreviaturas

CZTS:

Cu₂ ZnSnS₄

CZTSe:

Cu₂ ZnSnSe₄

CZTSSe:

Cu₂ ZnSn(S, Se)₄

FTIR:

Fourier transform infrared spectroscopy

IR:

Infrared

RF:

Radio frequency

SCs:

Solar cells

TFSCs:

Thin film solar cells

XRD:

X-ray diffraction

Modulación de las propiedades de anisotropía óptica y electrónica de ML-GaS por campo eléctrico vertical Modelo de retención de TaO / HfO x y TaO / AlO x RRAM con características de interruptor autorrectificante