Comprensión del filtrado digital con microcontroladores integrados

Conozca los métodos ampliamente utilizados para filtrar y procesar muestras de datos en el dominio del tiempo mientras observa más de cerca el motor Dual Biquad IIR de la unidad PowerQuad en el MCU LPC55S69.

Cuando se trata de muestras de datos recopiladas a lo largo del tiempo, o en el dominio del tiempo, una de las operaciones más básicas es "filtrar" los datos. Es importante comprender las formas comunes en que los datos se pueden filtrar digitalmente para lograr los mejores resultados y liberar una CPU para realizar otras tareas, especialmente cuando se trata de microcontroladores integrados.

En este artículo, conozca los métodos ampliamente utilizados para filtrar y procesar muestras de datos en el dominio del tiempo. Además, eche un vistazo más de cerca al motor Dual Biquad IIR de la unidad PowerQuad en la MCU LPC55S69, un bloque de construcción DSP versátil útil en muchos casos de uso de filtrado.

Filtros comunes para datos muestreados continuamente

Cuando se toman muestras de datos en el dominio del tiempo, los datos se recopilan continuamente a una tasa fija conocida. Los filtros de dominio de tiempo aceptan estos datos como entrada y emiten una nueva señal que se modifica de alguna manera. La salida de un filtro es simplemente otra señal en el dominio del tiempo, que puede procesarse más o transferirse a un convertidor de digital a analógico (DAC).

Por lo general, nos acercamos a los filtros en términos de cómo responden a las ondas sinusoidales. Si consideramos que una señal de entrada es una onda sinusoidal simple, el filtro puede ajustar la amplitud de la entrada así como también ajustar su fase. Al aplicar una señal compleja al filtro, ajustará la amplitud y la fase de los componentes sinusoidales de la señal. La forma en que se comporta el filtro en un rango de frecuencias se denomina respuesta de frecuencia.

Una operación estándar en el dominio del tiempo es realizada por los llamados filtros de Respuesta de Impulso Finito (FIR), que mezclan la muestra de datos más reciente con los elementos recolectados previamente para obtener la siguiente muestra de salida.

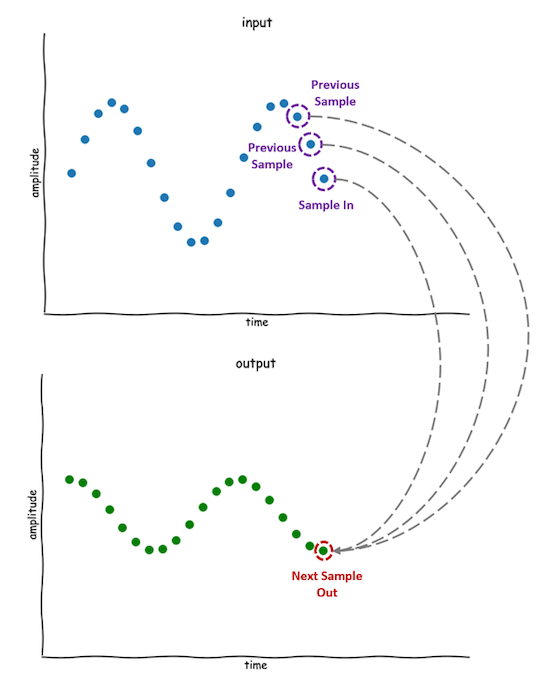
Figura 1. Procesamiento de filtro de muestra por muestra utilizando un historial de la entrada.

Una forma de implementar dicho filtro es almacenar muestras anteriores en una matriz y combinarlas usando una ecuación sencilla:

x [n] // La entrada más reciente
x [n-1], x [n-2] // Las dos muestras de entrada anteriores
y [n] // La siguiente salida muestra

y [n] =b0 * x [n] + b1 * x [n-1] + b2 * x [n-2]

Este fragmento de pseudocódigo en particular combina la muestra más reciente con las dos muestras de datos anteriores. Multiplica cada muestra de datos con un coeficiente constante separado antes de sumar los resultados para obtener la siguiente muestra de salida. En resumen, esto representa una operación simple de multiplicar y acumular, donde los coeficientes constantes y la longitud del historial controlan la respuesta de frecuencia del filtro.

Al elegir los valores apropiados para los coeficientes, es posible construir varios tipos de filtros. Si el filtro atenúa las frecuencias altas, actúa como un filtro de paso bajo. Al atenuar las frecuencias bajas, el filtro resultante funcionará como un filtro de paso alto. También es posible combinar los dos enfoques, lo que dará como resultado un filtro de paso de banda.

Los filtros FIR son conceptualmente simples pero pueden requerir bastantes muestras de datos previas para lograr un control preciso sobre su respuesta de frecuencia. Si bien este filtro es fácil de entender e implementar, ejecutarlo en una CPU convencional puede resultar engorroso, especialmente con un historial de tamaño moderado. Esto se debe a que cada muestra requiere muchas operaciones de multiplicar y sumar para determinar la salida.

Un método para reducir la cantidad de historial requerido es utilizar las salidas de filtro determinadas previamente al calcular la siguiente muestra de salida. Esta es la raíz de otra clase de filtros digitales llamados filtros de respuesta de impulso infinito (IIR):

// Este ejemplo utiliza las convenciones de nomenclatura previamente establecidas
y [n] =b0 * x [n] + b1 * x [n-1] + b2 * x [n-2] + a1 * y [n-1] + a1 * y [n-2]

El ejemplo anterior es un caso especial del filtro IIR conocido como filtro biquad, un bloque de construcción común que se puede conectar en cascada para construir filtros más grandes. Este enfoque requiere menos coeficientes en comparación con un filtro FIR para lograr la respuesta de frecuencia deseada. Hay compensaciones especiales que se deben tener en cuenta al utilizar este enfoque. El uso de retroalimentación puede hacer que los filtros oscilen si los coeficientes no se seleccionan correctamente.

Además, existen muchas herramientas que pueden generar automáticamente los coeficientes para todos los casos de uso comunes. Es común encontrar "libros de cocina" para calcular los coeficientes de filtro.

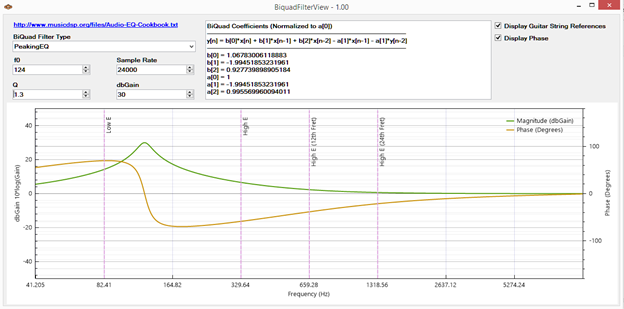
Figura 2. Una de las muchas herramientas que generan coeficientes automáticamente.

Uso de los motores Biquad PowerQuad IIR

La unidad LPC55S69 PowerQuad incorpora hardware dedicado para calcular filtros biquad IIR. El uso de PowerQuad para filtrar las muestras de datos recopiladas dejará a la CPU libre para realizar otras tareas.

Como se mencionó anteriormente, los algoritmos de filtrado no son complicados de implementar, pero pueden consumir mucho tiempo de CPU. La unidad PowerQuad del MCU LPC55S69 contiene hardware dedicado optimizado para muchas operaciones matemáticas complejas y de filtrado. Está conectado a través del bus AHB y la interfaz del coprocesador Arm® Cortex®-M33.

El entorno de desarrollo estándar para el LPC55S69 es el IDE MCUXpresso gratuito basado en eclipse. El SDK de LPC55S69 contiene muchos ejemplos útiles, algunos de los cuales son aplicaciones de ejemplo de PowerQuad.

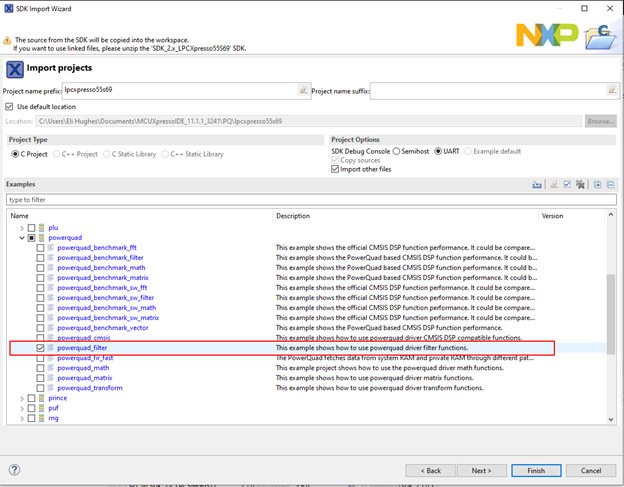
Figura 3. Selección del ejemplo de filtro digital PowerQuad.

El proyecto de ejemplo "powerquad_filter" contiene algunos ejemplos de diferentes configuraciones de filtros. El archivo "powerquad_filter.c" tiene varias funciones que demuestran configuraciones básicas de filtros.

Anteriormente, el artículo discutía un filtro que usa "Direct Form I", que es la implementación más sencilla. Sin embargo, el PowerQuad reorganiza el flujo de operaciones de multiplicar y sumar sin cambiar el resultado, lo que lleva a "Direct Form II", que no requiere que se almacene el historial de entradas y salidas. En su lugar, se almacena un historial intermedio v [n], también denominado estado de filtro.

Un puñado de registros en el bus AHB se utilizan para almacenar el estado y los coeficientes para configurar el PowerQuad para operaciones de filtro IIR. En los ejemplos de SDK, el estado del filtro se inicializa en la función PQ_BiquadRestoreInternalState.

Una vez que se completa, el filtro está listo para procesar muestras de datos. Esto se hace en la función PQ_VectorBiquadDf2F32 en fsl_powerquad_filter.c:

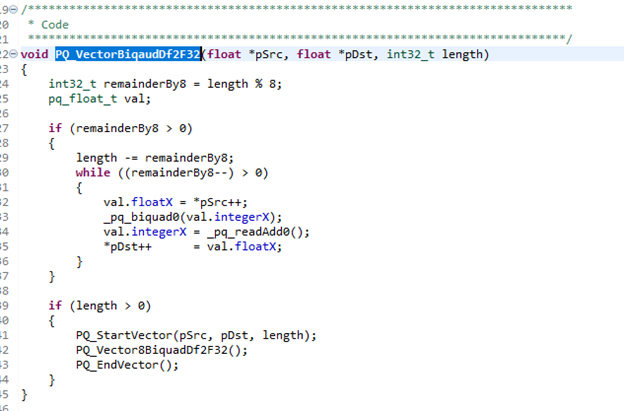
Figura 4. Implementación de filtros IIR vectorizados

Esta función está diseñada para procesar bloques de muestras de entrada en múltiplos de ocho. Los datos se pueden transferir desde un registro del núcleo de procesamiento principal del LPC55S69 a un coprocesador adjunto, que es el PowerQuad en este caso, con la ayuda de la instrucción MCR.

El PowerQuad hará el trabajo de filtrado, una forma mucho más eficiente de realizar muchas operaciones de multiplicación y adición de lo que hubiera sido en cualquiera de los núcleos Cortex-M33 del LPC55S69. Una vez que se realiza el PowerQuad, se puede acceder al resultado con la instrucción MCR, que mueve los datos de un coprocesador a un registro interno de la CPU.

El motor Dual Biquad IIR para filtrado digital

El MCU LPC55S69 viene con una unidad PowerQuad (que contiene dos motores biquad separados) que puede ayudar a acelerar el filtrado y las operaciones matemáticas complejas. Los registros de bus AHB se utilizan para configurar las funciones del PowerQuad IIR, y los datos se intercambian entre los núcleos PowerQuad y Cortex-M33 a través de la interfaz del coprocesador.

El SDK LPC55S69 en MCUXpresso es un buen punto de partida. Sin embargo, el código no está optimizado, ya que está destinado a ser fácil de entender. Tenga en cuenta que, si bien PowerQuad puede acelerar significativamente las aplicaciones de filtrado, la CPU aún debe transferir datos desde y hacia el coprocesador PowerQuad.

NXP tiene una útil herramienta de visualización y diseño de filtros Biquad IIR para ayudar a configurar el software. La página de la comunidad de NXP también ofrece una mirada en profundidad a la unidad PowerQuad de la MCU LPC55S69 y sus capacidades.

Los artículos de la industria son una forma de contenido que permite a los socios de la industria compartir noticias, mensajes y tecnología útiles con los lectores de All About Circuits de una manera que el contenido editorial no es adecuado. Todos los artículos de la industria están sujetos a estrictas pautas editoriales con la intención de ofrecer a los lectores noticias útiles, experiencia técnica o historias. Los puntos de vista y las opiniones expresados ​​en los artículos de la industria son los del socio y no necesariamente los de All About Circuits o sus redactores.