Robot Euler Angles:la base esencial

Es difícil entender las rotaciones de los robots, ¿no? Los ángulos de Euler son un dolor en el cuello. Aquí está la cartilla esencial para quitar el dolor.

¡Orientaciones! Solo me dan ganas de arrancarme el pelo. Si alguna vez has tenido que programar la pose final de un robot usando coordenadas y rotaciones, sabrás de lo que estoy hablando.

A primera vista, establecer la pose del efector final de su robot parece simple, ¿no es así?

Simplemente diga "Quiero mover la herramienta del robot a esto ubicación y quiero que apunte a esto dirección.”

Intuitivamente, usted sabe exactamente qué orientación desea que tenga la herramienta. Sin embargo, cuando se trata de describir la orientación usando números precisos, de repente esta simple tarea se convierte en un lío de confusión.

Por qué las orientaciones de los robots son difíciles de entender

Es fácil describir las coordenadas X, Y, Z (traslacionales) de la herramienta de un robot.

Para describir una traducción, simplemente ingrese las coordenadas, p. Point[X, Y, Z] =[100, 1000, 1500] mm, y solo hay una ubicación a la que esto podría referirse, suponiendo que esté utilizando la misma referencia base. Solo puede significar 100 mm en el eje X, 1 metro en el eje Y y 1,5 metros en el eje Z.

Pero, ¿cómo describe la orientación de la herramienta?

Podrías decir:
Rotación[XYZ] =[5, 45, 15]°
Sin embargo, podrías decir igualmente (redondeando los números)
Rot[XY'Z”] =[-7.9, 44.7, 16.2]°
o
Rot[ZY'Z”] =[7.9, 45.2, 5.0]°
o par
Cuaternión[q1-q4] =[0.9, -0.1, 0.4, 0.1]

 ¡Todos estos se refieren exactamente a la misma orientación!
Lo que lo hace aún más alucinante es que los diferentes fabricantes de robots usan convenciones diferentes. Todo puede convertirse en un dolor de cabeza, incluso si está familiarizado con la geometría 3D.

El problema:simplemente no pensamos en rotaciones

El verdadero problema es que no pensamos naturalmente en términos de rotaciones.

Intuitivamente entendemos las coordenadas traslacionales porque las usamos en nuestra vida diaria (por ejemplo, "Está en el segundo estante hacia abajo, cuatro libros desde la izquierda". ). Sin embargo, cuando tenemos que describir una orientación, recurrimos a señalar con el dedo y decir “Está en esa dirección”.

Desafortunadamente, los robots necesitan información más precisa que un vago “está ahí”.

Lo que necesitamos es una sólida comprensión de los ángulos de Euler.

¿Qué son los ángulos de Euler?

Demos un paso atrás y comencemos con lo básico.

El método más común para describir las orientaciones de los robots son los ángulos de Euler. Los ángulos de Euler consisten en tres números, cada uno de los cuales describe una rotación alrededor de un eje. Existen diferentes convenciones de ángulo de Euler según el orden de las rotaciones.

Primero, simplifiquemos esto a un ejemplo de un eje.

Imagina una brújula.

A menudo, el eje Z del mundo se refiere al eje que se extiende desde el cielo hasta el suelo. Entonces, puedes pensar que la aguja de una brújula es una rotación alrededor del eje Z (llamado Rot[Z]). Cuando sostienes la brújula plana frente a ti y la flecha apunta a 135°, significa que el norte está sobre tu hombro izquierdo, por lo que actualmente estás mirando hacia el sureste. No importa dónde coloques la brújula (en el suelo, en tu cabeza, etc.) si tiene la misma orientación, el ángulo siempre será de 135°.

Hasta ahora, así de simple.

Nuestra brújula solo tiene un valor de rotación (es decir, Rot[Z]), pero para describir cualquier orientación 3D necesitamos tres valores. Aquí es donde empieza a complicarse un poco más.

Otros métodos para describir las orientaciones de los robots son los cuaterniones o las poses (matrices de 4×4).

Pongámonos manos a la obra

De ahora en adelante, te será útil tener una ayuda visual interactiva.

Te sugiero que descargues una copia gratuita de RoboDK en este enlace, lo que hace que sea muy fácil visualizar marcos de referencia y ver las coordenadas resultantes.

Inicie RoboDK y cree un marco de referencia usando el botón "Agregar marco de referencia" o seleccionando la opción en el menú Programa. Debería ver un marco rojo, verde y azul en el centro de la pantalla.

Puede rotar el marco de esta manera:mantenga presionada la tecla Alt, luego haga clic y arrastre una de las flechas curvas que aparecen.

Cómo volar un avión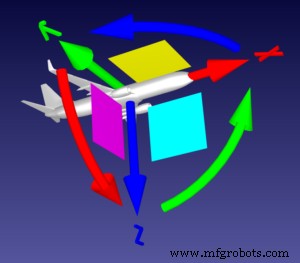

Usemos la analogía de un avión, como se describe muy claramente en el foro de robots.

Imagina que el marco de referencia es un plano. La punta de la flecha roja recta (el eje X) es la punta de su morro cónico y la flecha verde recta (el eje Y) es su ala izquierda.

En este caso, mover las flechas curvas cumple las siguientes funciones:

• Flecha roja curva =Rot[X]:El giro del avión, que permite que el avión gire sobre su eje horizontal.
• Flecha verde curva =Rot[Y]:El cabeceo del avión, que apunta el morro hacia arriba o hacia abajo.
• Flecha azul curva =Rot[Z]:la guiñada del avión, que determina la dirección en la que se dirige el avión.

Si el piloto quisiera que el avión girara hacia la izquierda y hacia abajo, gradualmente, el avión no solo giraría sobre el eje Z, no es así como funcionan los aviones.

En cambio, el avión:

1. Incline su morro hacia abajo:Rot[Y]
2. Rodar el avión a la izquierda:-Rot[X]
3. Guiñada a la izquierda:Rot[Z]

Todo este movimiento se representaría como Rot[XYZ]. Intenta mover el marco un poco tú mismo en RoboDK hasta que te sientas cómodo con estos conceptos.

Luego, haga doble clic en el nombre del marco en la parte superior izquierda de la ventana principal para que aparezca el panel "Detalles del marco".

Una orientación, varias rotaciones posibles

Usando RoboDK, intente las siguientes tareas.

Antes de cada tarea, restablezca el marco abriendo el ícono de menú "hamburguesa" (tres líneas horizontales) en el panel Detalles del marco y seleccionando "Restablecer (establecer identidad)".

1. Seleccione el menú desplegable en la parte superior de las coordenadas y elija la rotación Stäubli (X->Y'->Z") en lugar de Genérico.
2. Gire el marco para que el azul (Z) apunte hacia abajo y el rojo (X) apunte hacia atrás (es decir, ambos están volteados desde su posición inicial y el verde (Y) es el mismo que su posición inicial), pero solo entonces girando sobre el eje Y.
3. Restablezca el marco y luego muévalo nuevamente a la misma rotación. Sin embargo, esta vez solo use una rotación Z y luego una rotación X.
4. Restablezca el marco y luego muévalo nuevamente a la misma rotación. Sin embargo, esta vez solo use una rotación X y luego una rotación Z.

Como puede ver, puede haber más de una forma de lograr la misma orientación.

Al primer método lo podríamos llamar Rot[Y], ya que solo incluye una rotación sobre el eje Y. El segundo método lo podríamos llamar Rot[Z, X’], ya que incluye una rotación sobre el eje Z y una rotación sobre el nuevo eje X. Al tercero lo llamaríamos Rot[X, Z’]. El símbolo principal significa que la rotación ocurre con respecto al último movimiento en lugar de los ejes estáticos.

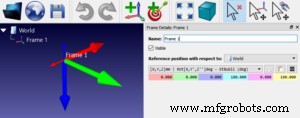
Este es el concepto fundamental detrás de los ángulos de Euler. Puede rotar un marco a la misma orientación de varias maneras cambiando la secuencia de ejes y rotaciones.

Diferentes fabricantes de robots han elegido diferentes combinaciones de rotaciones. Por ejemplo, Stäubli usa una convención XY'Z", Adept usa una convención ZY'Z", KUKA usa una convención ZY'X" y Fanuc &Motoman usan una convención XYZ. Por otro lado, ABB usa Quaternion y Universal Robots usa un vector de orientación. Pero todas las convenciones se pueden usar para representar cualquier orientación en el espacio.

Encontrarás más información en la Documentación de RoboDK.

Pruebe diferentes convenciones de robots

Con suerte, esto está empezando a tener sentido. Sin embargo, esto es solo el comienzo. Para dominar verdaderamente las convenciones de los ángulos de Euler en RoboDK, encuentro útil jugar con el software siguiendo esta guía.

Puedes ver el efecto de tus rotaciones en números en los cuadros azul claro, morado y amarillo en el panel "Detalles del marco".

De forma predeterminada, se elige la convención Genérica XYZ para los nuevos marcos de referencia. Intente seleccionar diferentes fabricantes de robots en el menú desplegable sobre los cuadros de colores. Intente ingresar valores numéricos en los cuadros para ver sus efectos en el marco de referencia.

Para un tutorial detallado sobre los ángulos de Euler, también puedo recomendar esta página en Mecademic.