Cálculos de voltaje y corriente

Existe una forma segura de calcular cualquiera de los valores en un circuito de CC reactivo a lo largo del tiempo.

Cálculo de valores en un circuito de CC reactivo

El primer paso es identificar los valores inicial y final para cualquier cantidad en la que el capacitor o inductor se oponga al cambio; es decir, cualquier cantidad que el componente reactivo intente mantener constante. Para los condensadores, esta cantidad es voltaje ; para inductores, esta cantidad es actual . Cuando el interruptor en un circuito está cerrado (o abierto), el componente reactivo intentará mantener esa cantidad al mismo nivel que estaba antes de la transición del interruptor, de modo que ese valor se utilizará para el valor de "inicio".

El valor final de esta cantidad es cualquiera que sea esa cantidad después de una cantidad de tiempo infinita. Esto se puede determinar analizando un circuito capacitivo como si el capacitor fuera un circuito abierto y un circuito inductivo como si el inductor fuera un cortocircuito porque así es como se comportan estos componentes cuando han alcanzado la "carga completa". después de un tiempo infinito.

El siguiente paso es calcular la constante de tiempo del circuito:la cantidad de tiempo que tardan los valores de voltaje o corriente en cambiar aproximadamente un 63 por ciento de sus valores iniciales a sus valores finales en una situación transitoria.

En un circuito RC en serie, la constante de tiempo es igual a la resistencia total en ohmios multiplicada por la capacitancia total en faradios. Para un circuito L / R en serie, es la inductancia total en henrys dividida por la resistencia total en ohms. En cualquier caso, la constante de tiempo se expresa en unidades de segundos y simbolizado por la letra griega "tau" (τ):

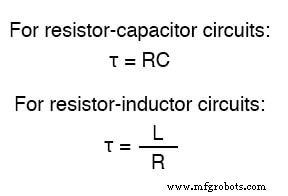
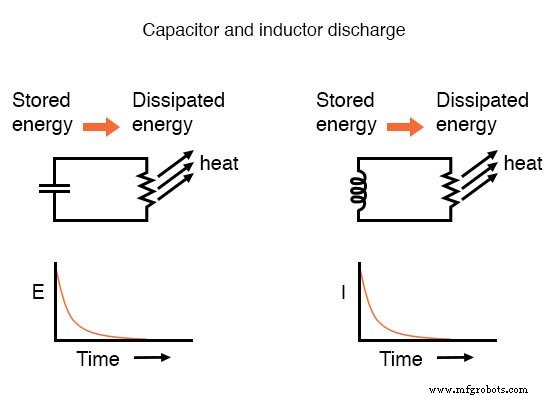
El aumento y la caída de los valores del circuito, como el voltaje y la corriente en respuesta a un transitorio, son, como se mencionó anteriormente, asintóticos . Siendo así, los valores comienzan a cambiar rápidamente poco después del transitorio y se estabilizan con el tiempo. Si se traza en un gráfico, la aproximación a los valores finales de voltaje y corriente forma curvas exponenciales.

Como se dijo antes, una constante de tiempo es la cantidad de tiempo que le toma a cualquiera de estos valores cambiar alrededor del 63 por ciento de sus valores iniciales a sus valores finales (últimos). Por cada constante de tiempo, estos valores se acercan (aproximadamente) un 63 por ciento a su objetivo final. La fórmula matemática para determinar el porcentaje exacto es bastante simple:

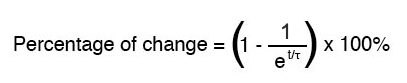
La letra e representa la constante de Euler, que es aproximadamente 2,7182818. Se deriva de técnicas de cálculo, después de analizar matemáticamente el enfoque asintótico de los valores del circuito. Después del valor de tiempo de una constante de tiempo, el porcentaje de cambio desde el valor inicial al valor final es:

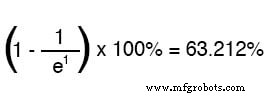
Después de dos constantes de tiempo, el porcentaje de cambio desde el valor inicial al valor final es:

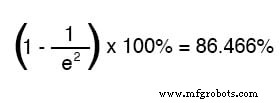
Después del valor de diez constantes de tiempo, el porcentaje es:

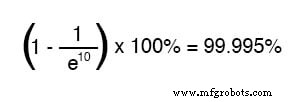
Cuanto más tiempo pase desde la aplicación transitoria de voltaje de la batería, mayor será el valor del denominador en la fracción, lo que hace que el valor de la fracción entera sea menor, lo que hace que un gran total (1 menos la fracción) se aproxime 1 o 100 por ciento.

Fórmula de constante de tiempo universal

Podemos hacer una fórmula más universal con esta para la determinación de valores de voltaje y corriente en circuitos transitorios, multiplicando esta cantidad por la diferencia entre los valores del circuito inicial y final:

Analicemos el aumento de voltaje en el circuito resistor-capacitor en serie que se muestra al comienzo del capítulo.

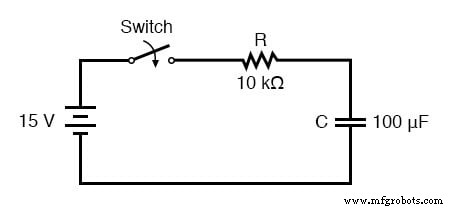
Tenga en cuenta que elegimos analizar el voltaje porque esa es la cantidad que los capacitores tienden a mantener constante. Aunque la fórmula funciona bastante bien para la corriente, los valores inicial y final de la corriente en realidad se derivan del voltaje del capacitor, por lo que calcular el voltaje es un método más directo. La resistencia es de 10 kΩ y la capacitancia es de 100 µF (microfaradios). Dado que la constante de tiempo (τ) para un circuito RC es el producto de la resistencia y la capacitancia, obtenemos un valor de 1 segundo:

Si el capacitor arranca en un estado totalmente descargado (0 voltios), entonces podemos usar ese valor de voltaje para un valor de “inicio”. El valor final, por supuesto, será el voltaje de la batería (15 voltios). Nuestra fórmula universal para el voltaje del capacitor en este circuito se ve así:

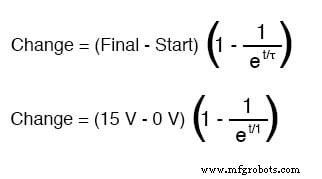
Entonces, después de 7.25 segundos de aplicar voltaje a través del interruptor cerrado, el voltaje de nuestro capacitor habrá aumentado en:

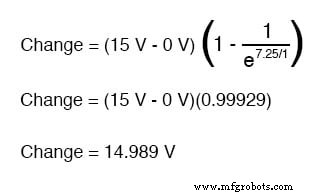
Dado que comenzamos con un voltaje de capacitor de 0 voltios, este aumento de 14,989 voltios significa que tenemos 14,989 voltios después de 7,25 segundos.

La misma fórmula también funcionará para determinar la corriente en ese circuito. Como sabemos que un condensador descargado actúa inicialmente como un cortocircuito, la corriente de arranque será la máxima cantidad posible:15 voltios (de la batería) divididos por 10 kΩ (la única oposición a la corriente en el circuito al principio):

También sabemos que la corriente final será cero, ya que el condensador eventualmente se comportará como un circuito abierto, lo que significa que eventualmente, no fluirán electrones en el circuito. Ahora que conocemos los valores de corriente inicial y final, podemos usar nuestra fórmula universal para determinar la corriente después de 7.25 segundos de cierre del interruptor en el mismo circuito RC:

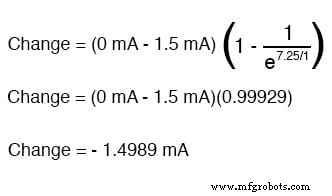
Tenga en cuenta que la cifra obtenida para el cambio es negativa, ¡no positiva! Esto nos dice que la corriente disminuyó en lugar de incrementarse con el paso del tiempo. Dado que comenzamos con una corriente de 1,5 mA, esta disminución (-1,4989 mA) significa que tenemos 0,001065 mA (1,065 µA) después de 7,25 segundos.

También podríamos haber determinado la corriente del circuito en el tiempo =7.25 segundos restando el voltaje del capacitor (14.989 voltios) del voltaje de la batería (15 voltios) para obtener la caída de voltaje a través de la resistencia de 10 kΩ, luego calculando la corriente a través de la resistencia (y la circuito en serie completo) con la Ley de Ohm (I =E / R). De cualquier manera, deberíamos obtener la misma respuesta:

Uso de la fórmula de la constante de tiempo universal para analizar circuitos inductivos

La fórmula de constante de tiempo universal también funciona bien para analizar circuitos inductivos. Aplicémoslo a nuestro circuito L / R de ejemplo al comienzo del capítulo:

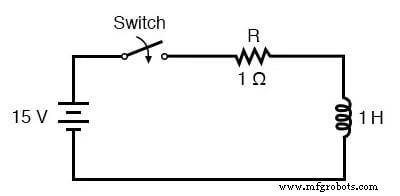
Con una inductancia de 1 henry y una resistencia en serie de 1 Ω, nuestra constante de tiempo es igual a 1 segundo:

Debido a que este es un circuito inductivo y sabemos que los inductores se oponen al cambio en la corriente, estableceremos nuestra fórmula de constante de tiempo para los valores iniciales y finales de la corriente. Si comenzamos con el interruptor en la posición abierta, la corriente será igual a cero, por lo que cero es nuestro valor de corriente inicial.

Después de que el interruptor se ha dejado cerrado durante mucho tiempo, la corriente se estabilizará a su valor final, igual al voltaje de la fuente dividido por la resistencia total del circuito (I =E / R), o 15 amperios en el caso de este circuito. .

Si deseáramos determinar el valor de la corriente en 3.5 segundos, aplicaríamos la fórmula de la constante de tiempo universal como tal:

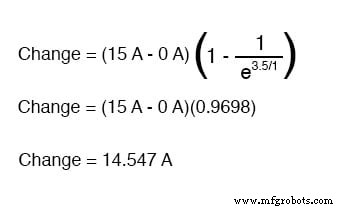
Dado el hecho de que nuestra corriente inicial era cero, esto nos deja en una corriente de circuito de 14,547 amperios en 3,5 segundos.

La mejor manera de determinar el voltaje en un circuito inductivo es calculando primero la corriente del circuito y luego calculando las caídas de voltaje en las resistencias para encontrar lo que queda por caer en el inductor. Con solo una resistencia en nuestro circuito de ejemplo (que tiene un valor de 1 Ω), esto es bastante fácil:

Restado de nuestro voltaje de batería de 15 voltios, esto deja 0.453 voltios a través del inductor en un tiempo =3.5 segundos.

REVISAR:

• Fórmula de constante de tiempo universal:
• Para analizar un circuito RC o L / R, siga estos pasos:
• (1):Determine la constante de tiempo para el circuito (RC o L / R).
• (2):Identifique la cantidad que se va a calcular (cualquier cantidad cuyo cambio se oponga directamente al componente reactivo. Para los capacitores, es voltaje; para los inductores, es la corriente).
• (3):Determine los valores inicial y final para esa cantidad.
• (4):Ingrese todos estos valores (Final, Inicio, tiempo, constante de tiempo) en la fórmula de constante de tiempo universal y resuelva para cambio en cantidad.
• (5):si el valor inicial era cero, entonces el valor real en el momento especificado es igual al cambio calculado dado por la fórmula universal. De lo contrario, agregue el cambio al valor inicial para averiguar dónde se encuentra.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de circuitos constantes de tiempo
• Hoja de trabajo de cálculos de constantes de tiempo

Ver nuestra colección de Calculadoras de energía en nuestro Herramientas sección.