Simulación de dinámica molecular en el mecanismo de corte en el proceso de mecanizado híbrido de silicio monocristalino
Resumen
En este trabajo se realizan simulaciones de dinámica molecular para investigar el mecanismo de corte durante el proceso de mecanizado híbrido combinado con los asistentes térmicos y de vibración. Se aplica un modelo de corte modificado para estudiar el comportamiento de remoción de material y la formación de daños en el subsuelo en un ciclo de vibración. Los resultados indican que durante el proceso de mecanizado híbrido, el mecanismo de eliminación de material dominante podría transformarse de extrusión a cizallamiento en un solo ciclo de vibración. Con un aumento de la temperatura de corte, se suprime eficazmente la generación y propagación de grietas, mientras que el hinchamiento aparece cuando el mecanismo dominante de eliminación de material se convierte en cizallamiento. El mecanismo de formación del daño subsuperficial en un ciclo de vibración puede ser distinto según la distribución de la tensión. Además, la generación de vacíos en la pieza de trabajo se hace evidente con el aumento de temperatura, que es un fenómeno importante en el proceso de mecanizado híbrido.
Introducción
El silicio monocristalino es un material semiconductor importante, que se ha utilizado ampliamente en sistemas de óptica infrarroja, microelectrónica y optoelectrónica debido a sus excelentes propiedades ópticas y mecánicas [1, 2]. Sin embargo, debido a la naturaleza de dureza y fragilidad del silicio monocristalino, se pueden generar fracturas microscópicas y daños en el subsuelo durante el mecanizado mecánico. Durante el proceso de micro-fresado, se pueden generar defectos de astillado del borde del tipo interior inducidos por el mecanizado en la pieza de trabajo [3]. En el mecanizado de corte de diamante monocristalino (SPDT), se puede formar una capa dañada en un rango de 200 a 600 nm dependiendo de los parámetros de procesamiento [4, 5]. Aunque la capa de daño subsuperficial se puede reducir a aproximadamente 50 nm mediante esmerilado y pulido. La eficiencia del mecanizado y la capacidad para fabricar estructuras complejas son limitadas. Para superar estos problemas, se han propuesto y probado varias tecnologías de mecanizado de asistencia. En particular, el corte asistido por calor (TAC) [6] y el corte asistido por vibración (VAC) [7] han atraído una gran atención por su extraordinario rendimiento de corte.
Para materiales frágiles como el silicio monocristalino, la transición de frágil a dúctil se puede promover cuando se aumenta la temperatura de mecanizado. Durante el proceso TAC, la pieza de silicio se ablanda térmicamente, lo que provoca la disminución de las fuerzas de corte [8] y la energía de corte específica [9, 10]. Mientras tanto, el recocido de las fases de alta presión en la fase de silicio cúbico se hace evidente cuando se aumenta la temperatura de mecanizado [11]. Con la selección adecuada de los parámetros de mecanizado, TAC puede lograr la superficie mecanizada deseada con alta pureza de fase y bajo daño del subsuelo [12,13,14]. Además del TAC, el corte asistido por vibración (VAC) es otro método de promoción para lograr una superficie de alta calidad en silicio monocristalino. Esta técnica se ha aplicado en la industria manufacturera desde la década de 1960 [15]. En el desarrollo inicial de esta tecnología, en el mecanizado solo se practicaba un movimiento de vibración lineal en la dirección de corte nominal, que se denomina corte por vibración lineal (LVC). En 1994, Shamoto y Moriwaki [16] propusieron el corte por vibración elíptica (EVC). A continuación, se han verificado las posibilidades de mecanizado de EVC en muchos materiales frágiles como silicio [17, 18], carburo de silicio unido por reacción [7], carburo de tungsteno [19, 20] y acero endurecido [21]. Durante el proceso de EVC, el daño subsuperficial puede suprimirse eficazmente, ya que la profundidad de corte transitoria (DOC) es mucho menor que la DOC nominal [22]. Además, debido a la separación en cada ciclo de vibración, las superficies de contacto entre la herramienta de corte y la pieza de trabajo quedan expuestas al gas o fluido circundante, lo que disipa el calor de corte generado. Por lo tanto, el desgaste de la herramienta de corte, como la adhesión y la reacción termoquímica [23], se puede suprimir de forma eficaz.
Para mejorar aún más la maquinabilidad de materiales frágiles, se han realizado experimentos de maquinado híbrido (HM) de combinación del asistente térmico y de vibración [24, 25]. Se encontró que al cortar Inconel 718 mediante el método HM, la rugosidad de la superficie mecanizada se puede reducir de manera efectiva [26]. Mediante experimentos y simulaciones del método de elementos finitos (FEM), se puede lograr una caída sustancial de las fuerzas de corte y una calidad superior de la superficie de las aleaciones de titanio durante el proceso HM [27]. Estos resultados demuestran la viabilidad del método HM en el mecanizado de precisión de materiales frágiles. Sin embargo, es difícil observar y medir directamente las variables físicas durante el proceso de mecanizado, ya que la herramienta de corte vibra a alta frecuencia y la zona de deformación está a alta temperatura. Además, en la fabricación de superficies nanométricas, el espesor de eliminación de material transitorio suele oscilar entre subnanómetros y unos pocos nanómetros. Por lo tanto, la representación tradicional del continuo del problema como FEM es cuestionable ya que los efectos de la mecánica cuántica se hacen evidentes.
En los últimos años, la simulación de dinámica molecular (MD) se ha aplicado ampliamente en las investigaciones del proceso de mecanizado asistido debido a sus ventajas en el estudio del proceso de corte nanométrico [28, 29, 30]. Según simulaciones anteriores de TAC [31], cuando se aumenta la temperatura de corte, la anisotropía en la fuerza de corte, la energía de corte específica y la tensión de fluencia se vuelven más obvias. Mientras tanto, la fuerza de corte en la pieza de trabajo es menor a una temperatura de corte más alta, lo que conduce a zonas de corte más estrechas y mayores magnitudes del ángulo del plano de corte [32]. Además, la velocidad de eliminación de material se puede mejorar aumentando la temperatura de corte, ya que se forman más virutas [33]. Para el proceso EVC, se ha descubierto mediante simulación MD que el esfuerzo de compresión y el esfuerzo cortante en la región de deformación pueden reducirse en gran medida en comparación con el corte ordinario [34], que es ventajoso para la supresión de daños subsuperficiales. Además, el proceso EVC muestra un adelgazamiento evidente de las virutas de corte, lo que da como resultado un aumento en la relación entre el grosor de la viruta sin cortar y el grosor de la viruta cortada [35]. Además, se ha descubierto que los parámetros de vibración, incluidas las relaciones de amplitud, las frecuencias de vibración y las diferencias de fase, tienen una gran influencia en el rendimiento de eliminación de material [34, 36].
Estos notables logros han mejorado la comprensión del mecanismo de mecanizado para el proceso de mecanizado asistivo. Sin embargo, para ahorrar tiempo de cálculo y memoria, los sistemas de simulación suelen ser bastante pequeños. En simulaciones anteriores del proceso EVC, las amplitudes de vibración y el DOC nominal son inferiores a 5 nm [22, 36]. Por lo tanto, el espesor de eliminación de material transitorio suele ser inferior a 1 nm, lo que no describe con precisión el proceso de eliminación de material real. Además, no se ha informado de las simulaciones MD del proceso HM. El mecanismo del proceso de remoción de material y la formación de daños subsuperficiales durante el proceso de HM aún no está claro. Por lo tanto, en este artículo, se lleva a cabo una simulación de MD para revelar el mecanismo de corte del proceso HM. El modelo de corte clásico se modifica para que los parámetros de vibración estén mucho más cerca de los valores experimentales, por ejemplo, la amplitud de vibración se amplía a 40 nm con una velocidad de corte nominal de 3,125 m / s. Se investigan el mecanismo de eliminación de material en un ciclo de vibración y la influencia del aumento de la temperatura de corte. La simulación de MD es realizada por el famoso Simulador Masivamente Paralelo Atómico / Molecular a Gran Escala (LAMMPS) [37]. El software de posprocesamiento OVITO [38] se emplea para analizar los resultados de la simulación.
Método de simulación
Detalles del modelo de corte
La Figura 1 muestra el diagrama esquemático del proceso EVC, que fue presentado originalmente por Shamoto et al. [39]. La trayectoria de la herramienta se puede expresar como:
$$ x \ left (t \ right) =A _ {{\ text {c}}} \ sin \ left ({2 \ pi ft} \ right) - vt $$ (1) $$ z \ left (t \ derecha) =A _ {{\ text {d}}} \ sin \ left ({2 \ pi ft + \ varphi} \ right) $$ (2)donde x ( t ) y z ( t ) representan el desplazamiento de la herramienta de corte en la x y z direcciones. A c y A d son la amplitud de vibración en la dirección de corte nominal ( x dirección) y la dirección nominal de DOC ( z negativo dirección). Parámetros f , v , φ y t representan la frecuencia de vibración, la velocidad de corte nominal, la diferencia de fase y el tiempo de simulación, respectivamente. El tiempo de simulación t i representa el tiempo del punto P i en la trayectoria de la herramienta de la Fig. 1.
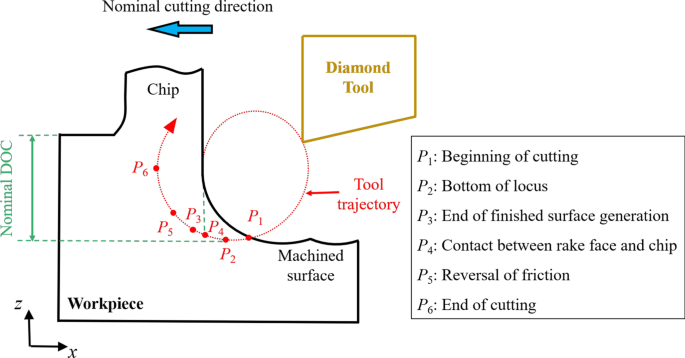
El diagrama esquemático del proceso EVC
Según la relación geométrica [40], el valor de t 1 y t 3 puede ser determinado por:
$$ x \ left ({t_ {1}} \ right) {-} x \ left ({t_ {3}} \ right) =2 \ pi v / \ omega $$ (3) $$ z \ left ( {t_ {1}} \ right) {-} z \ left ({t_ {3}} \ right) =0 $$ (4)Entonces, t 6 se puede obtener cuando la dirección de movimiento transitorio de la herramienta de diamante es paralela a la cara de inclinación de la herramienta:
$$ \ frac {{A _ {{\ text {c}}} \ sin (2 \ pi ft_ {6}) + v}} {{A _ {{\ text {d}}} \ sin (2 \ pi ft_ {6} + \ varphi)}} =\ tan \ gamma $$ (5)donde γ es el ángulo de inclinación de la herramienta de corte de diamante.
El modelo MD está presente en la Fig. 2. La pieza de silicio monocristalino está configurada como cuerpo deformable. Mientras que la herramienta de diamante se considera un cuerpo rígido, ya que el desgaste de la herramienta se puede despreciar en esta simulación. La morfología de la pieza de trabajo en el modelo de corte clásico se reforma de acuerdo con la trayectoria de la herramienta en el ciclo de vibración anterior teniendo en cuenta el radio del filo de la herramienta. La trayectoria de la herramienta se puede determinar como se ilustra en la Fig. 2b. P o y P b son el centro y el punto inferior del círculo del borde de la herramienta. Cuando se considera el efecto de borde de la herramienta, el punto de generación de superficie transitoria P c varía a lo largo del borde de la herramienta durante el movimiento de la herramienta. La superficie acabada real es generada por la línea envolvente del filo de la herramienta de corte. Si la trayectoria de P b se expresa mediante las ecuaciones. (1) y (2), la trayectoria de P c se puede calcular mediante [41]:
$$ x _ {{\ text {c}}} \ left (t \ right) =A _ {{\ text {c}}} \ sin \ left ({2 \ pi ft} \ right) - vt - r \ sin \ theta \ left (t \ right) $$ (6) $$ z _ {{\ text {c}}} \ left (t \ right) =A _ {{\ text {d}}} \ sin \ left ({ 2 \ pi ft + \ varphi} \ right) + r (1 {-} \ cos \ theta \ left (t \ right)) $$ (7)donde
$$ \ sin \ theta \ left (t \ right) =\ frac {{z ^ {{\ prime}} (t)}} {{\ sqrt {x ^ {{\ prime}} (t) ^ {2 } + z ^ {{\ prime}} (t) ^ {2}}}} $$ (8) $$ \ cos \ theta \ left (t \ right) =\ frac {{- x ^ {{\ prime }} (t)}} {{\ sqrt {x ^ {{\ prime}} (t) ^ {2} + z ^ {{\ prime}} (t) ^ {2}}}} $$ (9 )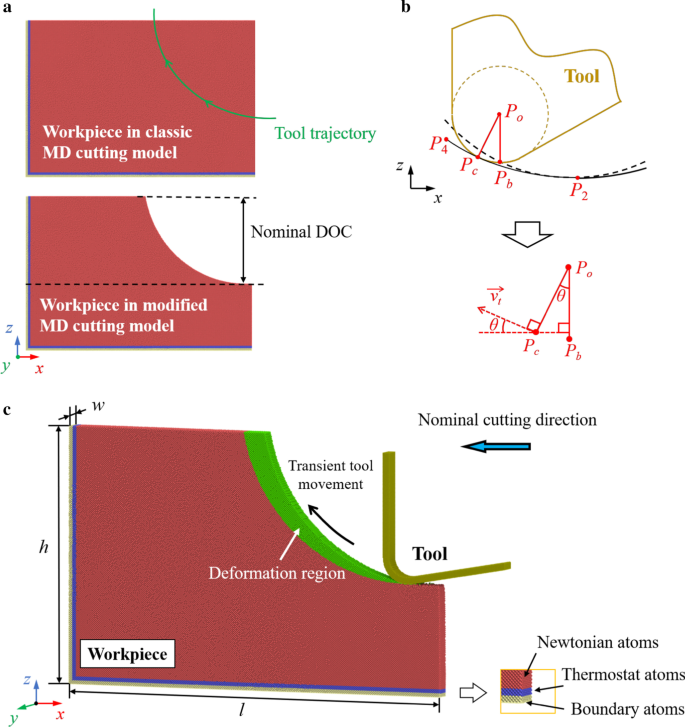
Esquema del modelo de corte MD. un Modificación de la pieza de trabajo. b Determinación de la trayectoria de la herramienta. c La morfología del modelo MD modificado. Los átomos verdes representan la región de deformación en un ciclo de vibración
Los átomos de silicio se dividen en tres grupos:átomos de límite, átomos de termostato y átomos de Newton. Los átomos del límite se fijan en sus posiciones equilibradas para sujetar la pieza de trabajo durante la simulación. Los átomos del termostato se mantienen a temperatura ambiente para disipar el calor de corte generado, mientras que los átomos newtonianos siguen la segunda ley de Newton.
Los detalles de los parámetros de simulación se enumeran en la Tabla 1. La longitud l y altura h se determinó mantener suficiente distancia entre la zona de corte y los límites fijos. La condición de límite periódica se aplica a lo largo de y dirección para imitar el silicio a granel. La dirección de corte nominal, el ángulo de inclinación / holgura de la herramienta y la diferencia de fase se determinaron con referencia a la configuración experimental [42]. La amplitud de vibración y el DOC nominal se amplían para acercarse a la escala experimental con un costo de simulación aceptable. Mientras tanto, para asegurar el espesor del material eliminado (átomos verdes en la Fig. 2c), la relación de velocidad y la frecuencia de vibración se establecieron en 40 y 500 MHz, respectivamente. Por lo tanto, la velocidad de corte nominal se determinó en 3,125 m / s. Además, se realizan simulaciones con diferentes temperaturas de corte para revelar el efecto del asistente térmico en el mecanismo de corte. La temperatura de corte aumenta de 300 a 1200 K, lo que se puede realizar durante el mecanizado asistido por láser tipo TAC [4, 11].
En este modelo modificado, solo se simula la etapa de corte durante el ciclo de vibración y se guardan los pasos de tiempo cuando la pieza de trabajo se separa con la herramienta de corte. Por lo tanto, la potencia de cálculo se puede concentrar en el proceso de corte transitorio. Lo más importante es que el proceso de eliminación de material transitorio se puede describir con precisión. En la Tabla 2 se muestra una comparación entre el modelo modificado y el modelo MD clásico.
Función potencial
En la simulación de MD, es importante adoptar un potencial sólido para describir la interacción entre átomos. Para el silicio monocristalino, los estudiosos han desarrollado muchos potenciales, como el método de átomo incrustado modificado (MEAM) [45], Stillinger-Weber (SW) [46], Tersoff [47] y la carga optimizada de muchos cuerpos (COMB) [ 48] potenciales. Entre estos potenciales, el potencial analítico de orden de enlace (ABOP) propuesto por Erhart y Albe [49] ha atraído una atención creciente. Es una función de potencial de tres cuerpos que permite la formación y ruptura de uniones durante la simulación de mecanizado. Según investigaciones anteriores [50], el ABOP puede describir con precisión las propiedades tanto del dímero como del volumen del silicio. Mientras tanto, las propiedades mecánicas del silicio fabricadas por el ABOP son consistentes con los experimentos bien [31], lo cual es importante en simulaciones MD de mecanizado a nanoescala. Por lo tanto, en este artículo, el potencial ABOP se aplica para describir las interacciones silicio-silicio y carbono-carbono. Mientras tanto, la interacción de silicio-carbono se describe mediante el potencial Morse, que se ha demostrado como un potencial eficiente en la simulación de corte a nanoescala [51, 52]. La función potencial de Morse se puede expresar como:
$$ E _ {{\ text {Si - C}}} \ left ({r_ {ij}} \ right) \, =D _ {{\ text {M}}} \ left [{{\ text {e}} ^ {{- 2a (r_ {ij} - R _ {{\ text {M}}})}} - 2 {\ text {e}} ^ {{- a (r_ {ij} - R _ {{\ text { M}}})}}} \ derecha] $$ (10)donde D M , a, y R M representa la energía de cohesión, el módulo de elasticidad y la distancia de equilibrio entre átomos, respectivamente. Los parámetros para el potencial Morse son [53]: D M =0,435 eV, a =46.487 nm −1 , R M =0,19475 nm.
Resultados y discusión
Rendimiento de corte
En el corte ordinario, el mecanismo dominante de eliminación de material puede verse muy influido por el grosor de la viruta no deformada [54]. Con un pequeño grosor de viruta no deformada, el mecanismo de eliminación de material dominante es la extrusión. La fase estable metálica (Si-II) puede generarse mediante la transición de fase de alta presión (HPPT), que facilita la deformación dúctil del silicio. Cuando aumenta el grosor de la viruta no deformada, el material se puede eliminar principalmente mediante un proceso de cizallamiento. Durante el proceso de EVC, dado que el grosor de la viruta no deformada varía constantemente, el mecanismo de eliminación de material puede transformarse de extrusión a cizallamiento en un ciclo de vibración. La Figura 3 muestra las instantáneas de la simulación de corte a 300 K. La estructura cristalina de la pieza de trabajo está determinada por el análisis de vecino común (CNA) [55]. Este análisis encuentra átomos que están dispuestos en una red de diamante cúbica o hexagonal. La estructura sin diamante de la Fig. 3c, e contiene principalmente la fase amorfa (a-Si), Si-II y otros átomos defectuosos [56]. Estas estructuras son inestables y se transformarán en a-Si después del corte. Se puede observar en la Fig. 3b, c que el material se elimina principalmente mediante extrusión en la etapa de corte inicial. Se puede observar un punto de estancamiento transitorio cerca del borde de la herramienta de corte. De manera similar al corte ordinario, los materiales en la región de deformación se dividen por el punto de estancamiento en virutas y material comprimido. A medida que avanza la herramienta de corte, aumenta el grosor de la viruta no deformada. Se generan planos de cizallamiento y granos de policristales en la pieza de trabajo, lo que indica que el cizallamiento se convierte en el mecanismo de eliminación de material dominante.
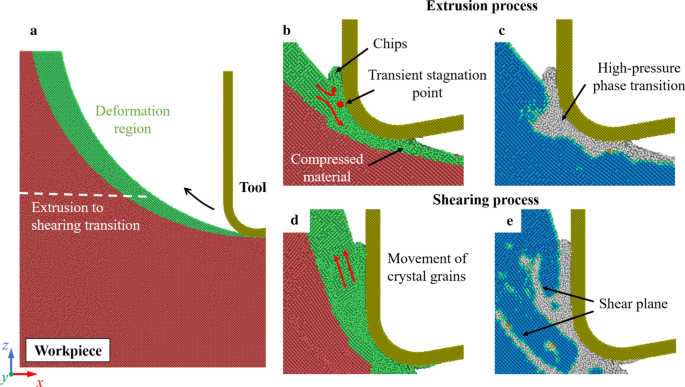
Transición del mecanismo de remoción de material. un Ilustración de la región de deformación. b , d Proceso de extrusión y cizallamiento. c , e Identificación de la estructura cristalina en pieza. Los átomos azules representan la estructura cúbica de diamante, mientras que los átomos grises están en la estructura sin diamante
La figura 4 muestra la morfología de la pieza de trabajo a diferentes temperaturas de corte. A 300 K, se pueden observar grietas y fracturas obvias en la pieza de trabajo durante el movimiento hacia arriba de la herramienta. Para materiales frágiles como el silicio monocristalino, el movimiento ascendente de la herramienta provocaría el desprendimiento de materiales y dejaría defectos en la pieza de trabajo, lo que se considera un problema específico en EVC [42]. Aunque estas grietas pueden eliminarse mediante más ciclos de vibración, la estabilidad del mecanizado se verá afectada debido a la irregularidad de la superficie de la pieza de trabajo. Cuando se aumenta la temperatura de corte, se suprime eficazmente la generación y propagación de grietas. De la Fig. 4d, no se detecta ninguna fractura obvia cuando la temperatura de corte aumenta a 1200 K. Sin embargo, se observa que a 900 K y 1200 K, el hinchamiento de la superficie mecanizada se vuelve obvio cuando el mecanismo de remoción de material se transforma en cizallamiento. Se puede concluir que a medida que se generan más granos de cristal en la etapa de cizallamiento, el hinchamiento puede ser causado por la rotación de estos granos de cristal a alta temperatura.
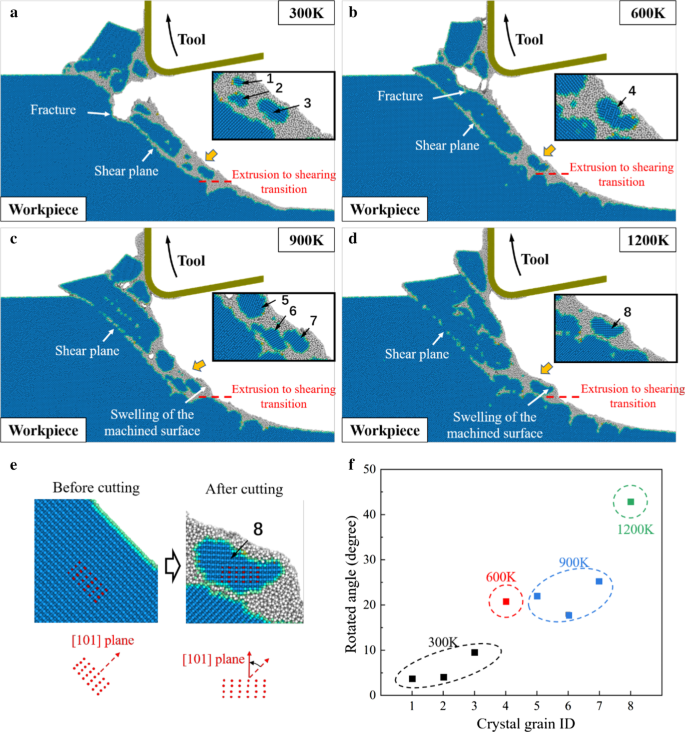
Morfología de la pieza de trabajo del proceso HM en a 300 K. b 600 K. c 900 K. d 1200 K. Los átomos azules representan la estructura cúbica de diamante, mientras que los átomos grises tienen una estructura que no es de diamante. e Determinación del ángulo de rotación de los granos de cristal. f El ángulo de rotación con el aumento de la temperatura de corte
Para una descripción clara de esta rotación, las coordenadas de 24 átomos marcados (átomos rojos) en los granos de cristal se utilizan para calcular el ángulo de rotación promedio, como se ilustra en la Fig. 4e. El ángulo de rotación de 8 granos de cristal (numerados en las Fig. 4a-d) se resume en la Fig. 4f. Se puede observar que el ángulo de rotación aumenta obviamente a temperatura elevada. Durante el proceso de HM, la viscosidad del a-Si se puede reducir considerablemente a alta temperatura y el movimiento ascendente de la herramienta promueve el movimiento hacia arriba de los átomos de la pieza de trabajo. Por lo tanto, se mejora el flujo atómico en la pieza de trabajo y se puede facilitar la rotación de los granos de cristal, lo que conduce al hinchamiento de la superficie mecanizada. Para restringir la rotación de los granos de cristal, se debe controlar la potencia de calentamiento para evitar el sobrecalentamiento de la pieza de trabajo. Además, los parámetros de vibración deben elegirse con cuidado, por ejemplo, se debe aplicar una velocidad de corte nominal más pequeña y una frecuencia de vibración más alta para suprimir la generación de granos de cristal y eliminar el hinchamiento mediante ciclos de vibración adicionales. Como se ilustra en la Fig.5, con los parámetros de vibración apropiados, P 1 podría ubicarse en la etapa de extrusión y la superficie mecanizada final se genera mediante extrusión sin hinchamiento.
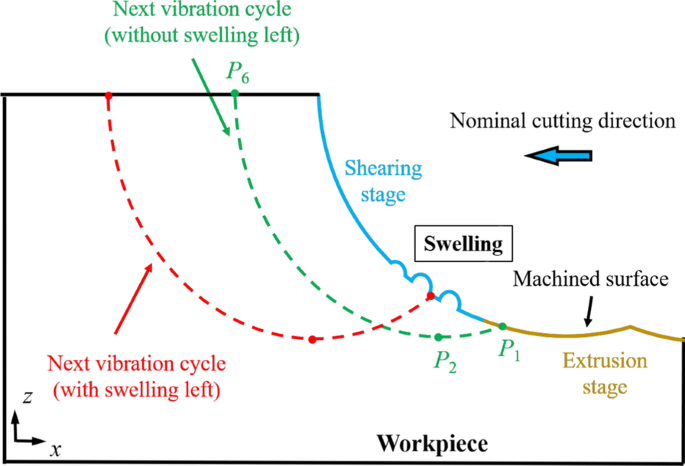
Eliminación de hinchazón en proceso HM
Campo de tensión en la pieza de trabajo
Para investigar más a fondo el mecanismo de corte durante el proceso HM, se calculó la distribución de esfuerzos en la pieza de trabajo. En la simulación de MD, la tensión hidrostática se puede expresar como:
$$ \ sigma _ {{{\ text {hidrostático}}}} =\, (\ sigma_ {x} + \ sigma_ {y} + \ sigma_ {z}) / 3 $$ (11)donde σ x , σ y y σ z , son tensores de tensión de los datos de salida de LAMMPS.
La distribución de la tensión hidrostática durante las etapas de extrusión y cizallamiento se muestra en la Fig. 6. Y se marcaron los valores máximos de las tensiones en las regiones de compresión y tracción. Con el movimiento de la herramienta, el punto de contacto entre la herramienta y la pieza de trabajo varía a lo largo del ciclo del borde de la herramienta, lo que da como resultado el movimiento de la región de compresión desde el borde de la herramienta hasta la cara de desprendimiento. Siguiendo informes anteriores, la HPPT de la fase de silicio monocristalino (Si-I) a Si-II podría ocurrir a presiones que comienzan en 10-12 GPa [57, 58]. En la simulación de corte a 300 K, la tensión máxima de compresión en la etapa de extrusión y cizallamiento alcanzó 18,1 GPa y 17,6 GPa, respectivamente. Este resultado indica que la fase dúctil Si-II se puede generar durante el corte y el HPPT todavía existe en la etapa de corte. Además, en la etapa de extrusión, la tensión de tracción se concentra principalmente cerca del área de contacto entre la cara del flanco de la herramienta y la superficie mecanizada como resultado de la adhesión de los átomos de silicio y la superficie de la herramienta. A medida que la herramienta pasa a la etapa de cizallamiento, la región de tracción se agranda y la concentración de tensión de tracción en la pieza de trabajo subterránea aumenta considerablemente, lo cual es causado por el movimiento de tracción hacia arriba. Cuando se aumenta la temperatura de corte, se mejora la deformabilidad plástica del silicio monocristalino y se reduce la tensión interna en la pieza de trabajo. A medida que la temperatura aumenta de 300 a 1200 K, el esfuerzo de compresión máximo disminuyó 16.6% y 25% en la etapa de extrusión y cizallamiento. Mientras tanto, aunque la concentración de la tensión de tracción en la pieza de trabajo subterránea sigue siendo obvia, el valor máximo de la tensión de tracción aparentemente disminuye en más del 30%. Se ha informado de que la tenacidad a la fractura del silicio monocristalino puede aumentarse eficazmente a temperaturas más altas [59]. Por lo tanto, las grietas y fracturas causadas por el efecto de desprendimiento debido al movimiento hacia arriba de la herramienta se pueden suprimir de manera efectiva.
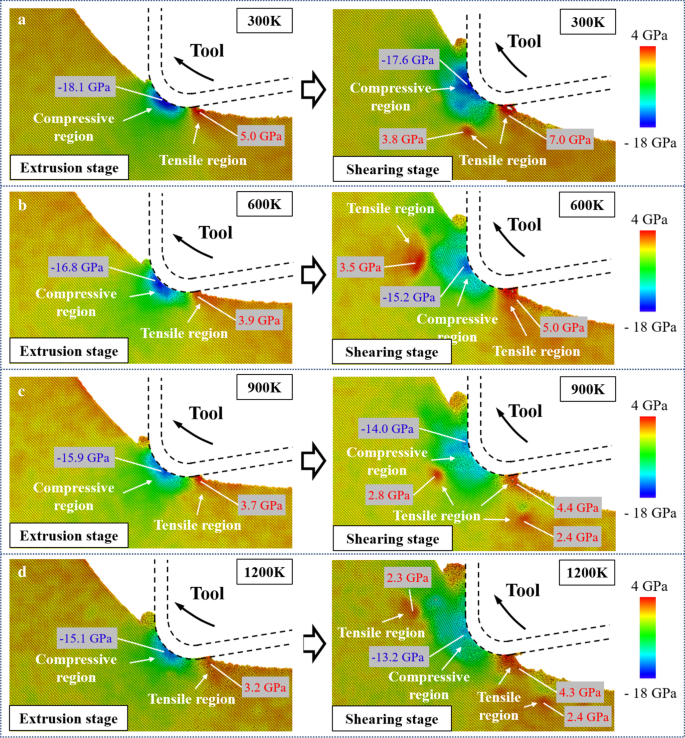
La distribución de la tensión hidrostática en: a 300 K. b 600 K. c 900 K. d 1200 K
El silicio monocristalino tiene una estructura cristalina Face Center Cubic (FCC) con 12 sistemas de deslizamiento. Según el movimiento de la herramienta, los principales sistemas de deslizamiento para la deformación por cortante son (111) / [\ (\ stackrel {\ mathrm {-}} {1} \) 01] y (1 \ (\ stackrel {\ mathrm {- }} {1} \) 1) / [\ (\ stackrel {\ mathrm {-}} {1} \) 01] sistemas. Por lo tanto, el componente de esfuerzo cortante resuelto τ s en el (111) / [\ (\ stackrel {\ mathrm {-}} {1} \) 01] se calcula el sistema de deslizamiento. Como se ilustra en la Fig.7, el componente de esfuerzo cortante resuelto τ s en la dirección M del plano de deslizamiento N se puede calcular mediante tensores de tensión mediante:
$$ \ tau _ {{\ text {s}}} =a_ {1} a_ {2} \ sigma_ {x} + b_ {1} b_ {2} \ sigma_ {y} + c_ {1} c_ {2} \ sigma_ {z} + \ left ({a_ {1} b_ {2} + a_ {2} b_ {1}} \ right) \ tau_ {xy} + \ left ({a_ {1} c_ {2} + a_ {2} c_ {1}} \ right) \ tau_ {xz} + \ left ({b_ {1} c_ {2} + b_ {2} c_ {1}} \ right) \ tau_ {yz} $$ (12)donde a 1 , b 1 , c 1 son los cosenos de dirección de la dirección normal del plano N mientras a 2 , b 2 , c 2 son los cosenos de dirección de la dirección de deslizamiento M . Mientras τ xy , τ xz y τ yz son los tensores de esfuerzo cortante de los datos de salida de LAMMPS.
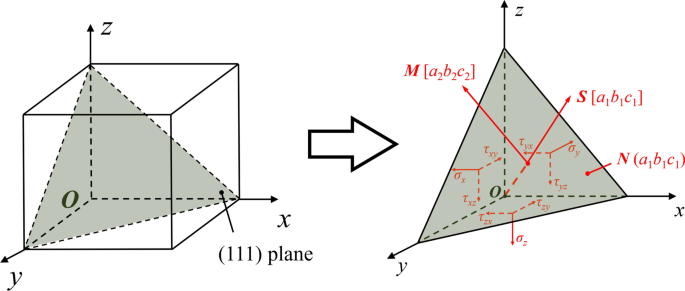
Ilustración de los tensores de tensión
La distribución del esfuerzo cortante resuelto τ s se muestra en la Fig. 8. La región con τ positivo s se define como la región de corte ya que se promueve el movimiento de deslizamiento a lo largo de la dirección [\ (\ stackrel {\ mathrm {-}} {1} \) 01], lo que facilita la remoción de material a través del corte. Mientras que la región con τ negativo s se considera la región de daño porque el movimiento de deslizamiento es preferible en la dirección opuesta, lo que lleva a la formación de daños en el subsuelo en la pieza de trabajo. En la etapa de extrusión, la tensión en la región de cizallamiento es menor que en la región de daño. El daño subsuperficial causado por la deformación por cizallamiento puede generarse debajo de la superficie mecanizada [60]. A medida que el movimiento de la herramienta de corte, el esfuerzo cortante a lo largo de la dirección [\ (\ stackrel {\ mathrm {-}} {1} \) 01] aumenta gradualmente, provocando la transición de remoción de material de extrusión a corte. Además, dado que la posición de la región dañada se mueve hacia arriba a lo largo del movimiento de la herramienta, el daño generado se puede eliminar mediante un ciclo de vibración adicional y no se dejará en la pieza de trabajo. Cuando la temperatura se incrementa de 300 K a 1200 K, el esfuerzo cortante en la región de daño disminuyó 36.1% y 42.4% en la etapa de extrusión y corte, respectivamente. En contraste, debido al movimiento hacia arriba de la herramienta, la disminución del esfuerzo cortante a lo largo de la dirección [\ (\ stackrel {\ mathrm {-}} {1} \) 01] en la etapa de corte es mucho menos aparente. El esfuerzo cortante resuelto crítico (CRSS) para el movimiento de deslizamiento se puede expresar como [61]:
$$ \ tau _ {{\ text {c}}} \ left (T \ right) =C \ varepsilon ^ {1 / n} \ exp \ left (\ frac {U} {nkT} \ right) $$ (13 )donde U y ε representan la energía de activación del movimiento de deslizamiento y la velocidad de deformación. Parámetros n y C son constantes materiales. Se puede concluir que el CRSS se puede disminuir obviamente al aumentar la temperatura. Por lo tanto, la deformación por cortante en la dirección [\ ({\ overline {\ text {1}}} \) 01] puede facilitarse a temperatura elevada.
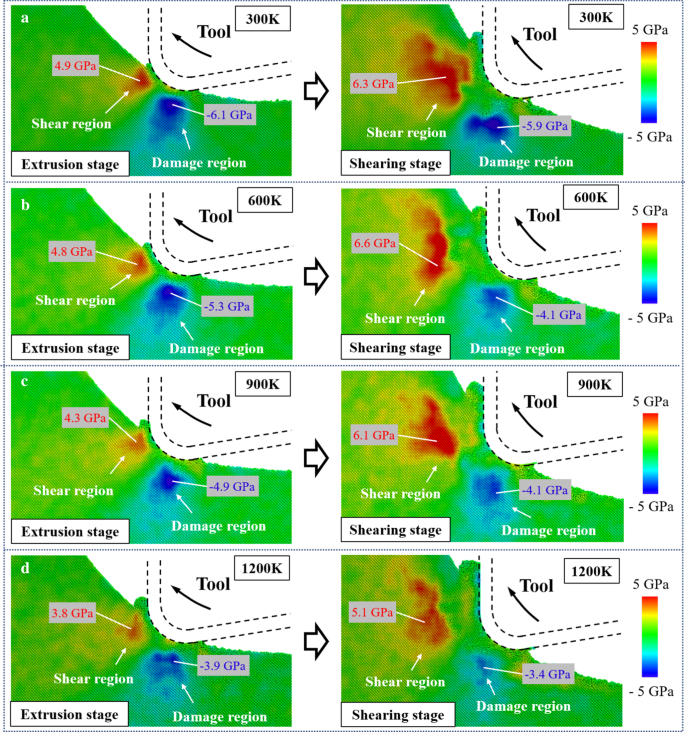
La distribución del esfuerzo cortante resuelto en: a 300 K. b 600 K. c 900 K. d 1200 K
Transición de fase
Cuando se aumenta la temperatura de corte, la transición de fase del silicio puede verse muy influenciada. La relajación del a-Si y la transición a Si-I pueden promoverse a una temperatura adecuada [62]. En la Fig. 4, el patrón de daño en las piezas de trabajo se vuelve más estrecho a alta temperatura. Una observación detallada del patrón de daño al cortar a 1200 K está presente en la Fig. 9a. Se observa que el daño generado en la región de deformación se recupera parcialmente después del corte, lo que indica que se ha producido la transición de la estructura sin diamante a Si-I. Y se generan más átomos de Si-I cuando se aumenta la temperatura de corte, como se muestra en la Fig. 9b. Además, la malla de la superficie construida (color rojo) [63] de la pieza mecanizada a 1200 K está presente en la Fig. 9c. Se observa que se forman algunas vacantes en la pieza de trabajo subterránea. Dado que los átomos están más empaquetados en la fase Si-I, la transición a Si-I podría causar una contracción del material, lo que induce a vacantes en la pieza de trabajo. El volumen de las vacantes a diferentes temperaturas se calcula y se presenta en la Fig. 9d. Se observa que casi no se generan vacantes a temperatura ambiente. Si bien se puede detectar un aumento obvio de las vacantes cuando la temperatura de corte aumenta a 900 K y 1200 K.
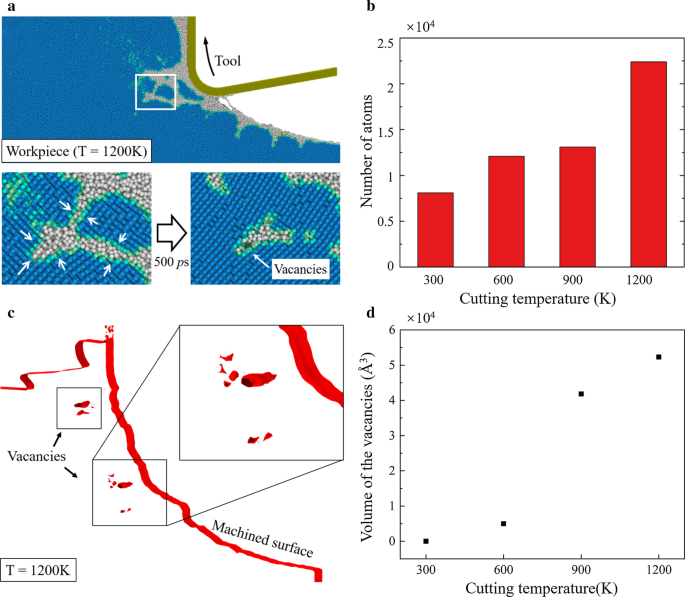
Proceso de relajación y vacantes en pieza. un Instantánea del patrón de daño de la pieza de trabajo a 1200 K. b Número de átomos transformados de la estructura sin diamante a la fase Si-I. c Malla de superficie construida de la pieza a 1200 K. d El volumen de las vacantes a diferentes temperaturas
En la Fig. 10 se presenta un análisis más detallado de las vacantes. Se elige un elemento de material debajo de la superficie mecanizada para monitorear la generación de vacantes. Están presentes el número de átomos en la estructura que no es de diamante y la evolución de la tensión del elemento material. Se concluye que durante el proceso de corte, el elemento de material se comprime primero y luego experimenta un esfuerzo de tracción debido al movimiento hacia arriba de la herramienta. Mientras tanto, se pueden observar dos picos del esfuerzo cortante a 300 K ya que el esfuerzo cortante en la región dañada aumenta a medida que pasa la herramienta de corte. Cuando se aumenta la temperatura de corte, la disminución del esfuerzo cortante es más obvia que el esfuerzo de tracción. A 1200 K, el segundo pico del esfuerzo cortante casi desaparece mientras que el esfuerzo de tracción se vuelve dominante en el elemento material durante el proceso de relajación.
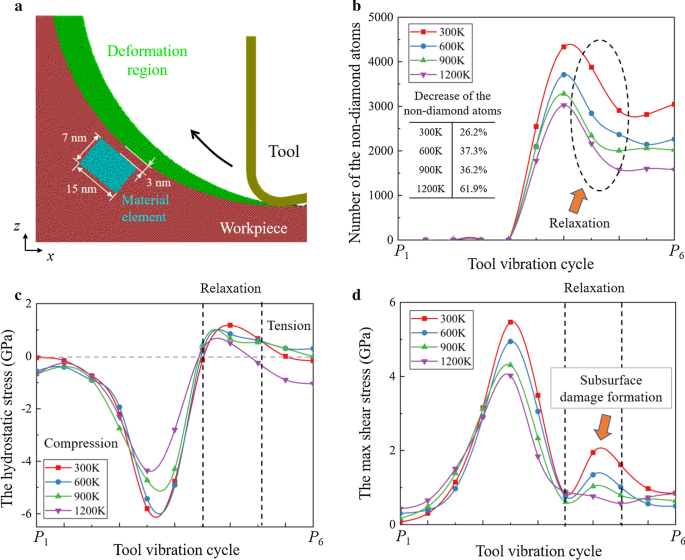
Relajación durante el proceso de HM. un Ilustración del elemento material. b Estadísticas de los átomos en estructura no diamantada en el elemento material. c , d Evolución de la tensión del elemento material
Para explorar el efecto de la tensión de tracción en el proceso de formación de las vacantes, se realizaron simulaciones de relajación de una muestra de silicio a granel. Como se muestra en la Fig. 11a, el modelo inicial se compone de un 40% de átomos de Si-I y un 60% de átomos de a-Si, que se genera mediante el método de fusión-enfriamiento [64]. El tamaño del modelo es 21,7 nm × 8,1 nm × 26,1 nm en x , años y z dirección, que contiene 230,400 átomos. The initial interface between crystal and non-crystal region is set as (001) crystal plane. Periodic boundary condition is applied in three dimensions to mimic bulk materials. The constructed surface mesh of the relaxed model is present in Fig. 11b. Furthermore, to quantify the vacancies, the solid volume fraction is calculated as the ratio of the solid material volume and the total volume of the simulation sample, as shown in Fig. 11c. It is observed that when temperature is increased, the solid volume fraction decreased obviously under tensile stress. Therefore, to suppress the vacancies, the desired cutting temperature in HM process should be lower than that in ordinary TAC. Meanwhile, the vibration parameters should be optimized to reduce the tensile stress in subsurface workpiece.
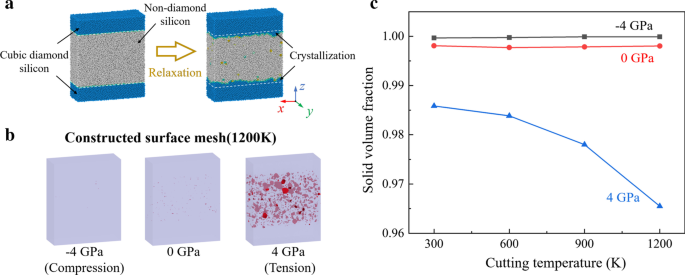
Relaxation simulation of silicon. un Scheme of MD relaxation simulation. b The surface mesh of the relaxed model at 1200 K. c The solid volume fraction curves
Conclusiones
In this paper, MD simulation is carried out to investigate the cutting mechanism of hybrid machining (HM) process. A modified cutting model is applied to reveal the material removal behavior and subsurface damage formation in one vibration cycle. The main conclusions were as follows:
- (1)
During HM process, the dominant material removal mechanism could transform from extrusion to shear in a single vibration cycle. With an increase of the cutting temperature, the generation and propagation of cracks can be effectively suppressed. However, the swelling appears when the dominant material removal mechanism becomes shearing, which is caused by the rotation of the crystal grains in workpiece.
- (2)
Based on the stress analysis, the dominant formation mechanism of the subsurface damage in one vibration cycle can be distinct. In the extrusion stage, the subsurface damage can be generated by the shear stress in the damage region. While in the shearing stage, tensile stress becomes dominant in subsurface damage formation. When the cutting temperature is increased, although the tensile stress concentration in the subsurface workpiece is still obvious, the peak value of the stresses is apparently decreased, which effectively suppress the cracks and fractures in workpiece.
- (3)
When the cutting temperature is increased, less subsurface damage is generated in the workpiece. However, due to the tensile stress, some vacancies can be generated in the workpiece when the cutting temperature is increased. Therefore, the desired cutting temperature during HM process should be lower than that in ordinary TAC and the vibration parameters should be set carefully to suppress the vacancies in the subsurface workpiece.
Disponibilidad de datos y materiales
The datasets used and analyzed in the current study can be obtained from the corresponding authors upon reasonable request.
Abreviaturas
- TAC:
-
Thermal assisted cutting
- VAC:
-
Vibration assisted cutting
- LVC:
-
Linear vibration cutting
- EVC:
-
Elliptical vibration cutting
- DOC:
-
Depth of cut
- HM:
-
Hybrid machining
- FEM:
-
Método de elementos finitos
- MD:
-
Dinámica molecular
- LAMMPS:
-
Simulador masivo paralelo atómico / molecular a gran escala
- MEAM:
-
Modified embedded-atom method
- SW:
-
Stillinger–Weber
- COMB:
-
Charge optimized many-body
- ABOP:
-
Analytical bond-order potential
- Si-II:
-
Metallic stable phase
- HPPT:
-
High-pressure phase transition
- CNA:
-
Análisis de vecinos comunes
- a-Si:
-
Amorphous phase
- Si-I:
-
Single-crystal silicon phase
- FCC:
-
Face Center Cubic
- CRSS:
-
Critical resolved shear stress
Nanomateriales
- ¿Cuál es el proceso de fabricación de herramientas de corte?
- Tipos y clasificación de procesos de mecanizado | Ciencias de la fabricación
- ¿Cuáles son los pasos principales del proceso de mecanizado?
- La importancia de la lubricación en el mecanizado de piezas mecánicas
- Comprender la precisión y el proceso de la tecnología de corte por láser
- Velocidad de avance frente a velocidad de corte:comprenda la diferencia
- La diferencia entre el proceso de mecanizado convencional y no convencional
- Comprender el proceso de torneado en el mecanizado CNC
- Una descripción general sobre el proceso de mecanizado de plástico
- Preparación para el proceso de fabricación de prototipos a producción
- Beneficios del proceso de corte por láser



