HOT Graphene y HOT Graphene Nanotubes:nuevos semimetales y semimetales de baja dimensión
Resumen
Reportamos un nuevo alótropo de grafeno llamado HOT grafeno que contiene hexágonos, octágonos y tetragones de carbono. También se construye una serie correspondiente de nanotubos enrollando el HOT hoja de grafeno. Los cálculos ab initio se realizan en estructuras geométricas y electrónicas del HOT el grafeno y el CALIENTE nanotubos de grafeno. El cono de Dirac y la alta velocidad de Fermi se logran en una estructura no hexagonal de HOT grafeno, lo que implica que la estructura alveolar no es una condición indispensable para que existan los fermiones de Dirac. CALIENTE Los nanotubos de grafeno muestran estructuras electrónicas distintivas según su topología. El (0,1) n ( n ≥ 3) CALIENTE Los nanotubos de grafeno revelan las características de los semimetales, mientras que el otro conjunto de nanotubos (1,0) n muestra espacios de banda continuamente ajustables (0 ~ 0.51 eV) con el tamaño del tubo. Una competencia entre el efecto de curvatura y la aproximación de plegado de zona determina los espacios de banda de (1,0) n nanotubos. La nueva conversión entre semimetalicidad y semiconductividad surge en tubos ultrapequeños (radio <4 Å, es decir, n <3).
Introducción
Debido a su flexibilidad de unión, los sistemas basados en carbono muestran un número ilimitado de estructuras diferentes con una variedad igualmente grande de propiedades físicas. Estas propiedades físicas son, en gran parte, el resultado de la dimensionalidad de estas estructuras [1]. El grafeno es una capa bidimensional única de átomos de carbono unidos en una estructura de celosía hexagonal [2] que revela una serie de propiedades únicas, como portadores sin masa, alta velocidad de Fermi [3] y conos de Dirac [4, 5], que son característica de los fermiones bidimensionales de Dirac. La celosía en forma de panal que consta de dos subredes de carbono equivalentes juega un papel crucial en la formación de propiedades tan intrigantes [2]. Enyashin e Ivanovskii [6] construyeron 12 redes de carbono bidimensionales artificiales, pero no encontraron estructuras distintas del alótropo grafino que exhiban el comportamiento electrónico similar al grafeno. Parece implicar que los fermiones tipo Dirac en sp 2 Los sistemas de carbono adherido dependen de la estructura alveolar. En la dimensión inferior, el nanotubo de carbono es una estructura alveolar enrollada en un cilindro hueco de diámetro nanométrico y μm de longitud [7,8,9,10]. Como hay un número infinito de formas de enrollar una hoja en un cilindro, la gran variedad de geometrías helicoidales posibles, que definen la quiralidad del tubo, proporciona una familia de nanotubos con diferentes diámetros y estructuras microscópicas [11,12,13]. Las propiedades electrónicas y de transporte se encuentran sin duda entre las propiedades físicas más importantes de los nanotubos de carbono y dependen fundamentalmente del diámetro y la quiralidad [14,15,16,17,18]. Los nanotubos de grafeno pueden ser semimetálicos [14] o semiconductores [19,20,21], con una banda prohibida que varía de cero a unas pocas décimas de eV, dependiendo de su diámetro y quiralidad [10, 14, 16]. Además, se puede demostrar que la banda prohibida de los tubos semiconductores está simplemente relacionada con el diámetro del tubo. Los nanotubos semimetálicos también mantienen las propiedades únicas del grafeno, como los portadores sin masa, la alta velocidad de Fermi [22] y los conos de Dirac [23]. Estos resultados notables pueden obtenerse a partir de una variedad de consideraciones, desde el llamado enfoque de plegado de bandas, basado en el conocimiento de las propiedades electrónicas de la hoja de grafeno, hasta el estudio directo de los nanotubos utilizando enfoques semiempíricos de unión estrecha [14, 16, 18, 23]. En comparación con cálculos ab initio más sofisticados y resultados experimentales disponibles, consideraciones más precisas, como efectos de curvatura, k F desplazamiento [24, 25], hibridación σ-π [26] se introducen. El grafeno y los materiales similares al grafeno [6] se consideran un material revolucionario para la futura generación de dispositivos electrónicos de alta velocidad, dispositivos lógicos de radiofrecuencia [27, 28], compuestos reforzados con conductividad térmica y eléctrica [29, 30], catalizador [31], sensores [32,33,34,35], electrodos transparentes [27, 36], etc. basándose en las propiedades inusuales de todo lo anterior. Durante las últimas décadas, los nanotubos de carbono también han mostrado un gran potencial en circuitos lógicos, almacenamiento de gas, catálisis y almacenamiento de energía debido a sus extraordinarias propiedades electrónicas, mecánicas y estructurales [37,38,39]. Por lo tanto, la creación de nuevos alótropos de carbono (incluidos 2D y 1D) ha sido el foco de numerosas exploraciones teóricas y experimentales debido a su importancia científica y tecnológica fundamental [40]. Sin embargo, aclarar completamente las estructuras de estas emocionantes fases de carbono a través de las tecnologías experimentales actuales suele ser poco realista debido a su cantidad limitada, así como a la mezcla de otras fases. La predicción teórica es necesaria y ha tenido un gran éxito [31, 32, 33, 34, 35, 40, 41, 42].
En este estudio, diseñamos un nuevo alótropo de grafeno que tiene fermiones de Dirac bidimensionales sin una estructura exclusivamente hexagonal. El nuevo alótropo se construyó con hexágonos, octágonos y tetragones de carbono entrelazados y se denominó HOT grafeno. CALIENTE Los nanotubos de grafeno también se construyeron enrollando HOT hoja de grafeno junto con diferentes direcciones. La propiedad electrónica, efecto de curvatura, k F efecto de cambio, etc. de HOT El grafeno y los nanotubos se calcularon mediante cálculos ab initio basados en la teoría de la función de densidad (DFT).
Método de cálculo
Los cálculos actuales sobre HOT grafeno y CALIENTE Los nanotubos de grafeno se realizaron utilizando un método de primeros principios basado en la teoría de densidad funcional (DFT) con la aproximación de gradiente generalizado (GGA) en la forma de intercambio-correlación funcional de Perdew-Burke-Ernzerh (PBE) [43], como implementado en el Paquete de Simulación Ab initio de Viena (VASP) [44, 45]. Las funciones de onda se expandieron en ondas planas hasta un límite de energía cinética de onda plana de 520 eV. Las integrales de la zona de Brillouin (BZ) se realizaron utilizando un esquema de muestreo Monkhorst-Pack [46] con un k resolución de malla de puntos de 2π × 0.03 Å - 1 . Los vectores base de la celda unitaria (que representan la forma y el tamaño de la celda unitaria) y las coordenadas atómicas se relajaron completamente en cada sistema hasta que las fuerzas en todos los átomos fueron menores que 0.01 eV / Å.
Resultados y discusión
Estructuras geométricas y electrónicas de HOT Grafeno
La estructura geométrica de HOT el grafeno (Fig. 1a) muestra una situación de unión más complicada que el grafeno. La variedad de polígonos de carbono en HOT el grafeno da como resultado varios caracteres de enlace de carbono. Estos polígonos en HOT el grafeno comparte bordes comunes entre sí, y los enlaces se pueden distinguir por los dos polígonos a los que pertenecen. Por lo tanto, en nuestra investigación, se denominan 6–8 enlaces, 4–8 enlaces, 4–6 enlaces, 6–6 enlaces y 8–8 enlaces. Los enlaces 4-8 y los enlaces 6-8 tienen dos longitudes de enlace diferentes:1,44 Å y 1,47 Å para 4-8 enlaces; 1,41 Å y 1,48 Å para 6–8 enlaces. Los enlaces 4–6, 6–6 enlaces y 8–8 enlaces tienen longitudes de enlace únicas de 1,44 Å, 1,46 Å y 1,34 Å, relativamente. La Figura 1b muestra la estructura de bandas y la densidad de estados (DOS) de HOT grafeno con el BZ correspondiente representado en la Fig. 1c. El punto de cruce de las bandas de energía en el nivel de Fermi indica la semimetalicidad de HOT grafeno, que es confirmado por la desaparición de DOS en el nivel de Fermi. El punto de Dirac está ubicado en (0, 0.0585, 0) adyacente a Γ. La estructura de la banda 3D (Fig. 2) presenta las superficies de la banda cerca del nivel de Fermi, donde se pueden ver los conos de Dirac formados por superficies cónicas superior e inferior que se encuentran en dos puntos de Dirac exactamente en la superficie de Fermi. La correspondiente velocidad de Fermi (v F ) de los fermiones de Dirac, evaluados a partir del gradiente de las dispersiones lineales de las estructuras de bandas, es 6.27 × 10 5 m / s, que es un poco más bajo que 8.1 × 10 5 m / s [22] para nanotubos de grafeno y 8,6 × 10 5 m / s [47, 48] para el grafeno. El alto v F implica una alta movilidad de los transportistas en el HOT grafeno.
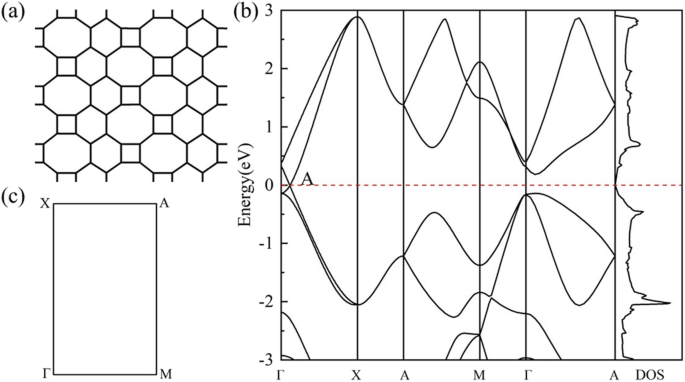
( a ) Geometría de HOT grafeno ( b ) Estructuras de banda y DOS del HOT grafeno ( c ) el BZ correspondiente de HOT grafeno
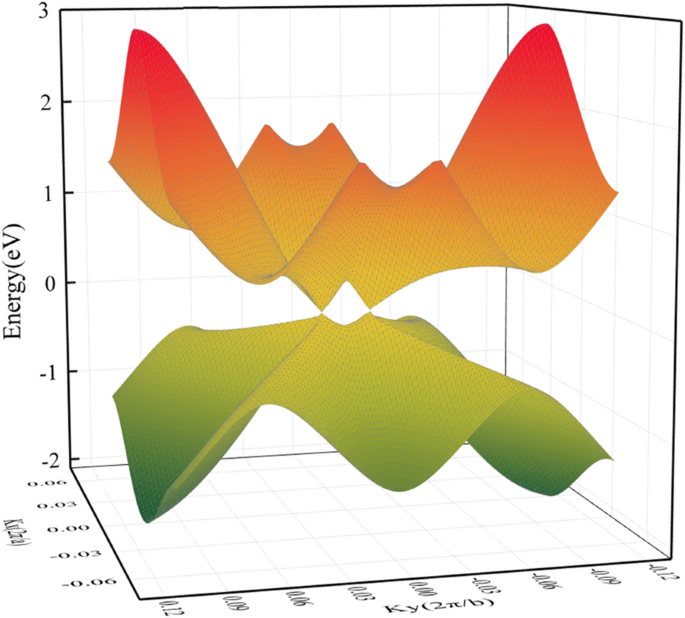
Estructura de banda 3D del HOT grafeno
Estructuras geométricas y electrónicas de HOT Nanotubos de grafeno
El CALIENTE Los tubos de grafeno se enrollan desde el HOT hoja de grafeno en varias direcciones simbolizadas por un índice en 2D HOT celosía de grafeno (Fig. 3a). Este índice se denota como ( l, m ) n basándose en dos vectores unitarios a y b . Símbolo ( l, m ) [18, 20, 21] significa diferentes direcciones en el HOT hoja de grafeno, n representa el número de unidades de perímetro (Fig. 3b yc) utilizadas para enrollar los tubos. Bajo la simetría de inversión espacial del HOT celda unitaria de grafeno, el símbolo de nanotubos se limita a 0 ≤ l y 0 ≤ m para evitar una correspondencia de varios a uno. El número de posibles estructuras geométricas del HOT nanotubos de grafeno es infinito ya que hay infinitas opciones para diámetros y direcciones de rodadura. Entre un número tan grande de nanotubos, en nuestro estudio solo se seleccionan dos direcciones (0,1, 1,0). Esto se debe a que la disposición helicoidal de los átomos en otras direcciones es apenas periódica y posee una longitud casi infinita de celda unitaria a lo largo del eje del tubo. Una celda unitaria tan grande no es realista en nuestros cálculos. Diferentes direcciones de rodadura entre (1,0) n y (0,1) n Los tubos dan lugar a diferencias en la geometría y la situación de unión. En la Fig. 3d ye se muestran dos tubos, (1,0) 6 y (0,1) 4, para describir las diferencias geométricas entre las dos direcciones de laminación. La disposición de los polígonos a lo largo de la dirección (1,0) se puede dividir en dos patrones:C 4 –C 6 –C 8 (naranja) y C 8 –C 6 –C 4 (azul) que son exactamente opuestos entre sí. Estos dos patrones opuestos se alternan a lo largo de la dirección circunferencial del tubo. En la dirección (0,1), los polígonos dispuestos a lo largo del eje del tubo también tienen dos patrones:C 4 –C 8 (azul) y C 6 –C 6 (naranja). Dos C 4 –C 8 los patrones se alternan con un C 6 –C 6 patrón a lo largo de la dirección circunferencial.
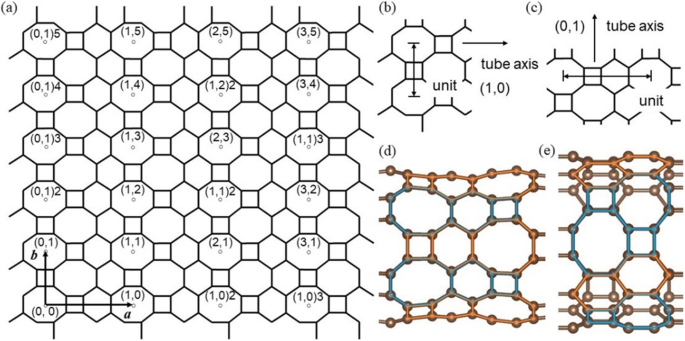
( a ) Los diferentes tubos se indican con el símbolo ( l, m ) n , con ( l, m ) significa dirección de balanceo basada en el vector unitario a y b y n para el número de unidades de diámetro del tubo; ( b ) unidad de diámetro en la dirección (1,0); ( c ) unidad de diámetro en la dirección (0,1); ( d ) estructura geométrica de un (1,0) 6 HOT nanotubo de grafeno; ( e ) estructura geométrica de un (0,1) 4 HOT nanotubo de grafeno
Para revelar el costo de energía al enrollar una hoja en tubos, definimos la energía de curvatura (Fig. 4) E cur como:
$$ {E} _ {\ mathrm {cur}} ={E} _ {\ mathrm {tubo}} ^ {\ mathrm {at}} - {E} _ {\ mathrm {hoja}} ^ {\ mathrm { en}} $$donde \ ({E} _ {\ mathrm {tube}} ^ {\ mathrm {at}} \) es la energía promedio de los átomos en nanotubos, y \ ({E} _ {\ mathrm {sheet}} ^ {\ mathrm {at}} \) es la energía promedio de los átomos en la hoja 2D. El (1,0) n Los tubos exhiben un menor costo de energía que los nanotubos de grafeno, mientras que el (0,1) n Los tubos son casi los mismos que los nanotubos de grafeno del sillón, excepto por varios tubos ultrapequeños. Estos resultados también sugieren que es posible sintetizar el HOT nanotubos de grafeno en experimentos. Cabe señalar que el tubo (1,0) 1 es demasiado pequeño porque su diámetro es incluso más corto que la longitud de enlace del carbono.
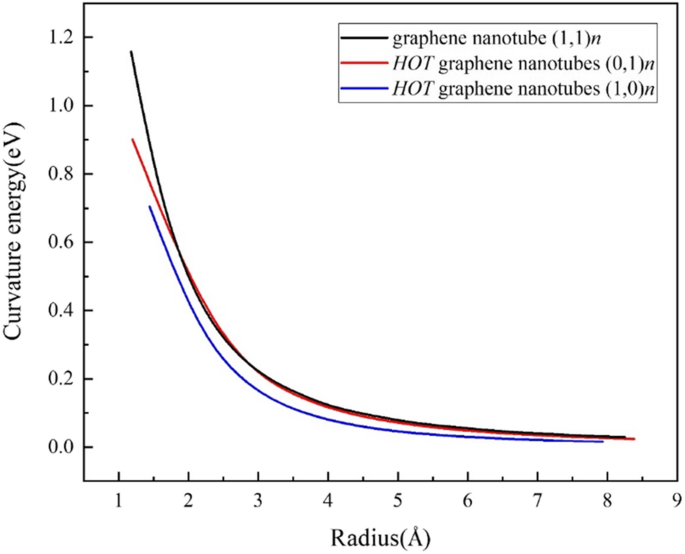
Energías de curvatura del HOT nanotubos de grafeno y nanotubos de grafeno
La estructura de banda electrónica calculada y el DOS del nanotubo (0,1) 6 (Fig. 5b) indican un carácter semimetálico. Cuando el CALIENTE La hoja de grafeno se enrolla en un nanotubo, su 2D BZ se reduce a 1D BZ como resultado de las nuevas condiciones de contorno periódicas en los nanotubos. Las condiciones de contorno periódicas a lo largo de la dirección circunferencial del tubo sólo permiten vectores de onda "alrededor" de la circunferencia de nanotubos y estos vectores se cuantifican [49]. Las condiciones de contorno periódicas a lo largo del eje de los nanotubos siguen siendo las mismas que las de la hoja 2D, luego los vectores de onda permanecen continuos a lo largo del eje de los nanotubos. Según el esquema de plegado de zonas, la estructura de la banda electrónica de un nanotubo específico viene dada por la superposición de las bandas de energía electrónica de la hoja 2D correspondiente a lo largo de la k específicamente permitida. líneas [50]. Como los vectores de onda cuantificados en el medio de la BZ del HOT el grafeno siempre cruza el punto de Dirac (punto F en la Fig. 5a), un punto de Dirac no degenerado (punto F en la Fig. 5b) y el cono de Dirac aparece en las estructuras de bandas de (0,1) n HOT nanotubos de grafeno, lo que resulta en la semimetalicidad de todos los (0,1) n nanotubos. El tubo (0,1) 6 se calcula para evaluar la semimetalicidad de este conjunto de (0,1) n nanotubos en la Fig. 5. Estructura de bandas de (0,1) 6 HOT Los nanotubos de grafeno muestran un punto de cruce de bandas de energía en el nivel de Fermi y el DOS correspondiente no muestra estados en el nivel de Fermi, lo que verifica la semimetalicidad del sistema. Como el cono de Dirac en (0,1) n tubos se origina en el HOT hoja de grafeno, la coordenada calculada del punto de Dirac en el (0,1) 6 nanotubos es la misma que en HOT hoja de grafeno que es (0, 0.0585, 0). La velocidad de fermi calculada en el punto de Dirac en (0,1) 6 nanotubos es 6,76 × 10 5 m / s, cerca de 6.27 × 10 5 m / s en el HOT hoja de grafeno.
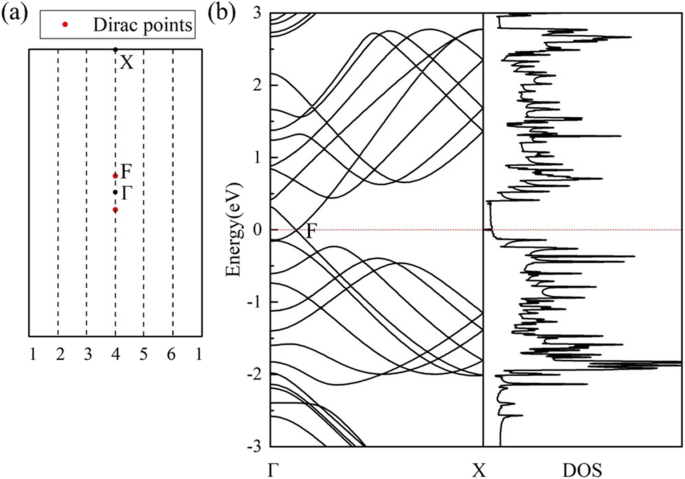
( a ) El primer BZ del HOT grafeno con k permitido líneas (líneas discontinuas) para el (0,1) 6 nanotubos. F es el punto de Dirac. ( b ) Las estructuras de bandas calculadas y DOS de (0,1) 6 nanotubos
La evolución de la estructura de bandas de (0,1) n nanotubos con diferentes radios de tubo (Fig. 6a) revela que el CALIENTE nanotubos de grafeno (0,1) n son semimetálicos ( n ≥ 3) y transformarse en metal ( n =2) y luego volver a semimetal ( n =1). Este cambio en un radio pequeño se debió al llamado efecto de curvatura [26]. En la situación de nanotubos ultrapequeños (por ejemplo, (0,1) 2 y (0,1) 1), la curvatura tiene un efecto no despreciable en el esquema de plegado de zonas. La longitud de enlace y el ángulo de enlace experimentan un cambio no despreciable dentro de la gran curvatura, lo que influye en la estructura de la banda electrónica. Las estructuras de bandas de tales nanotubos ya no son una simple superposición de bandas de energía en los vectores de onda permitidos. Este cambio de bonos modifica las condiciones que definen las k punto en el que las bandas ocupadas y desocupadas se cruzan (en un punto etiquetamos k F ) y mueva la k F lejos de los puntos de Dirac originales, que se llama k F efecto de cambio [24, 25]. Como resultado, en el (0,1) n HOT nanotubos de grafeno, el k F se aleja de su posición original ( k CALIENTE ) en el HOT hoja de grafeno (punto F en la Fig. 5a). Y la dirección de cambio de k F se calcula a lo largo del vector de onda permitido (líneas discontinuas en la Fig. 5a), lo que no produce cambios en la semimetalicidad (Fig. 6a ( n ≥ 3)). Según la coordinación calculada de los puntos de Dirac, el k F El efecto de desplazamiento se vuelve no despreciable en (0,1) 5 con un radio de tubo de 5.988 Å, cuyo punto de Dirac ( k F ) cambia a (0,0.0626,0) desde el punto original ( k CALIENTE ) en (0,0.0594,0) en HOT hoja de grafeno. A medida que el radio del tubo se hace más pequeño, la k F sigue cambiando y alcanza el punto (0,0.0712,0) en el tubo (0,1) 3. En el tubo (0,1) 2, el k F cambia a (0,0.0835,0) donde el punto de Dirac se mueve hacia abajo por debajo del nivel de Fermi, lo que resulta en un sistema metálico. La desaparición de la semimetalicidad en (0,1) 2 indica una desviación de la k F efecto de cambio en el (0,1) n nanotubos ( n ≥ 3). Además, el tubo (0,1) 1 se vuelve semimetálico nuevamente en su estructura de banda y el DOS (Fig. 6b). Nuestro análisis del estado de electrones del (0,1) n HOT nanotubos muestra estados π superpuestos en n ≥ 2, que generalmente se considera el origen de la semimetalicidad de los nanotubos de grafeno [18, 24]. Sin embargo, el análisis del estado de electrones correspondiente del HOT El nanotubo de grafeno (0,1) 1 muestra una hibridación σ-π en la que una banda baja σ * cruza el nivel de Fermi y se une al cono de Dirac (líneas azules en la Fig. 6a). La coordinación del punto de Dirac, que es (0,0.18345,0), también exhibe una distinción de otros (0,1) n HOT nanotubos de grafeno. La velocidad de Fermi calculada es 4,47 × 10 5 m / s, inferior a 6,27 × 10 5 m / s en HOT hoja de grafeno y valores para otros (0,1) n nanotubos (~ 6,76 × 10 5 Sra). En la figura 6a también se muestra una forma obviamente diferente de su estructura de banda. Todos estos personajes verifican que la semimetalicidad del HOT El nanotubo de grafeno (0,1) 1 se origina a partir de la hibridación σ-π. En resumen, con la curvatura creciente, la k F efecto de cambio emerge en n =5, se vuelve más eficaz a 4 ≥ n ≥ 2, y finalmente se reemplaza por el efecto de hibridación σ-π en n =1.
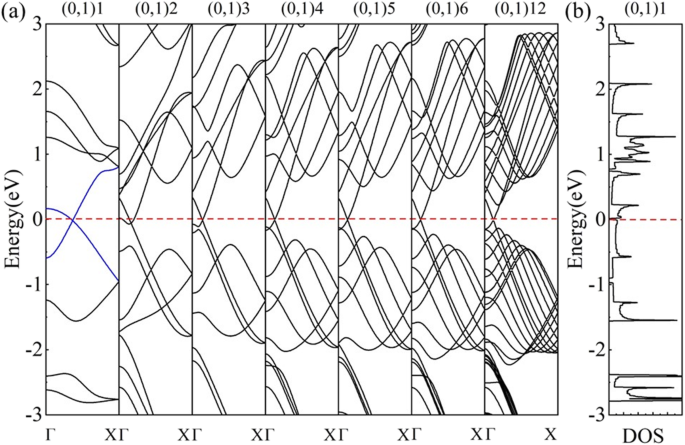
( a ) Evolución de la banda de (0,1) n nanotubos ( n =1, 2, 3, 4, 5, 6, 12); ( b ) DOS del (0,1) 1 nanotubo
En otra dirección de laminación, la estructura de banda calculada de (1,0) 6 (Fig. 7b) muestra semiconductividad. Los 6 vectores de onda (líneas discontinuas) son paralelos a Γ-M, cruzando el punto Г en el medio de la BZ de HOT grafeno (Fig. 7a) y abra una banda prohibida de 0,46 eV como se muestra en el DOS (Fig. 7b). En esta dirección de balanceo, los vectores de onda permitidos en el medio de BZ nunca incluyen los puntos de Dirac, lo que da como resultado espacios de banda distintos de cero en este conjunto de nanotubos. La evolución de la banda revela un cambio en los espacios de banda con diferentes radios en la Fig. 8a. El (1,0) n HOT Los nanotubos de grafeno son semiconductores ( n ≥ 4). El máximo de la banda de valencia (VBM) y el mínimo de la banda de conducción (CBM) se acercan del tubo (1,0) 6 al tubo (1,0) 4 y luego se cruzan entre sí en el tubo (1,0) 3 con un radio de 2,17 Å. Este punto de cruce está exactamente en el nivel de Fermi ubicado en (0.0791,0,0). El DOS calculado (Fig. 8b) presenta 0 estados al nivel de Fermi de (1,0) 3, verificando la semimetalicidad. Cuando el radio del tubo disminuye a (1,0) 2, se abre de nuevo un espacio de 0,848 eV. El CBM y VBM de (1,0) 2 están ubicados en el punto Γ y el punto M, respectivamente, lo que indica una banda prohibida indirecta. Este cambio en VBM implica un origen diferente para la semiconductividad en (1,0) 2. Un estudio adicional del cambio de banda prohibida en el (1,0) n HOT Los nanotubos de grafeno se muestran en la Fig. 9. La evolución de la banda prohibida en función de n (3 ≤ n ≤ 23) indica que la banda prohibida se puede ajustar con los tamaños de los tubos. Además, en lugar de ser monótona, la dependencia de la banda prohibida como el tamaño del tubo tiene una forma de zigzag (Fig. 9 curva negra). El mínimo global en (1,0) 15 presenta una brecha de banda cero. La semimetalicidad de (1,0) 15 se confirma además por la estructura de la banda y DOS (Fig. 9g). A partir del esquema de plegado de zonas, sabemos que la estructura de bandas de los nanotubos es la superposición de la estructura de bandas de la hoja 2D a lo largo de la k cuantificada correspondiente. líneas [50]. Por lo tanto, la semimetalicidad indica que al menos uno de los k permitidos líneas (líneas de trazos en la Fig. 7a) se cruzan con los puntos de Dirac (puntos rojos en la Fig. 7a) en n =15. De lo contrario, si el k permitido las líneas tienen una distancia de los puntos de Dirac ( k CALIENTE ), aparecerá una banda prohibida en nanotubos. Además, esta distancia entre k F y la k líneas es proporcional a los espacios de banda, ya que la dispersión de la banda cerca del cono de Dirac es lineal [25]. El Δk m mide la distancia más corta entre k F y k m líneas de número cuántico m . Calculamos esta distancia Δk m entre los puntos de Dirac ( k CALIENTE ) y las k permitidas líneas en el HOT grafeno y grafíquelo (línea roja) junto con los espacios de banda (línea negra) en la Fig. 9. En primer lugar, todos los k permitidos las líneas tienen un número cuántico m . Cuando n ≤ 7 (p. Ej., Fig. 9a), la distancia más corta ( Δk m ) está entre las k CALIENTE y las primeras k línea, k 1 , que se encuentra en el punto Γ constantemente (inserte el gráfico (a) en la Fig. 9). En esta situación, Δk m es constante ya que ambos k 1 y k CALIENTE son constantes independientes del tamaño del tubo. Sin embargo, como k permitido las líneas se vuelven más densas en nanotubos más grandes (7 ≤ n ≤ 17), la k 2 se convierte en el más cercano a k CALIENTE (por ejemplo, Fig. 9b). En esta situación, la k 2 se aproxima al punto de Dirac desde el exterior BZ con radios de tubo crecientes; por lo tanto, muestra una disminución de Δk m en la figura 9 (7 ≤ n ≤ 17). n =17 es un punto de inflexión donde k 2 casi se cruza con el punto de Dirac, lo que da como resultado un mínimo local de la distancia Δk m (Figura 9c). A medida que aumenta el radio, la k 2 atraviesa la k CALIENTE punto y continúa alejándose de él hasta el punto Г, lo que resulta en un aumento de la distancia de nuevo a 17 ≤ n ≤ 24 (por ejemplo, Fig. 9d). Al mismo tiempo, k 3 se acerca al punto de Dirac. k 3 se acerca a k CALIENTE de k 2 y comienza una nueva disminución en la distancia Δk m en n ≥ 24. Como los espacios entre bandas son proporcionales a esta distancia Δk m [25], la curva de banda prohibida muestra la misma forma que Δk m trama ( n ≥ 7). Y se revela que los intervalos de banda cambian en ciclos:el k m se acerca al punto de Dirac ( k CALIENTE ) provocando una disminución de la banda prohibida, luego atraviesa el punto de Dirac dando como resultado un mínimo local, luego se aleja más del punto de Dirac causando un aumento de la banda prohibida, y finalmente es reemplazado por la siguiente línea k m + 1 entrando en el siguiente ciclo. En resumen, la razón por la que los espacios entre bandas cambian con el tamaño del tubo ( n ≥ 7) es que el k las líneas se mueven con diferentes tamaños de tubo, por lo que cambia la distancia Δk m entre k CALIENTE y las k permitidas líneas que es proporcional a los espacios entre bandas.
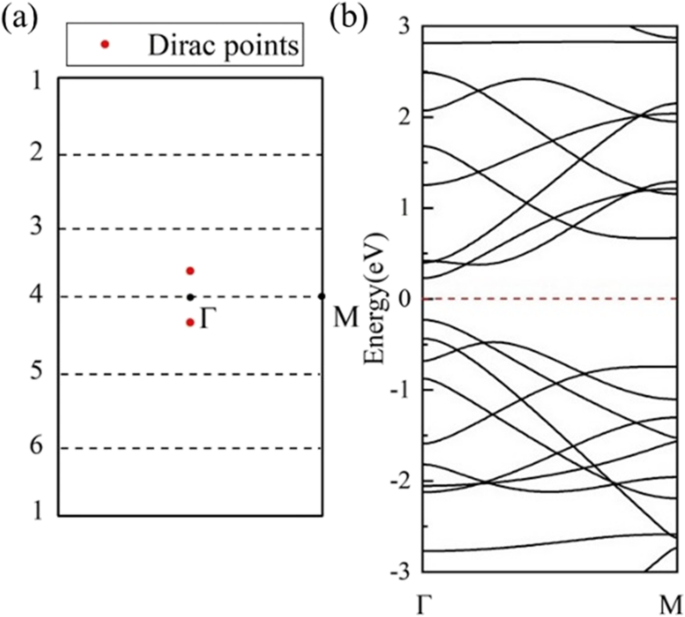
( a ) El primer BZ del HOT grafeno con k permitido líneas (líneas discontinuas) para el (1,0) 6 nanotubos; ( b ) estructuras de bandas del (1,0) 6 nanotubos
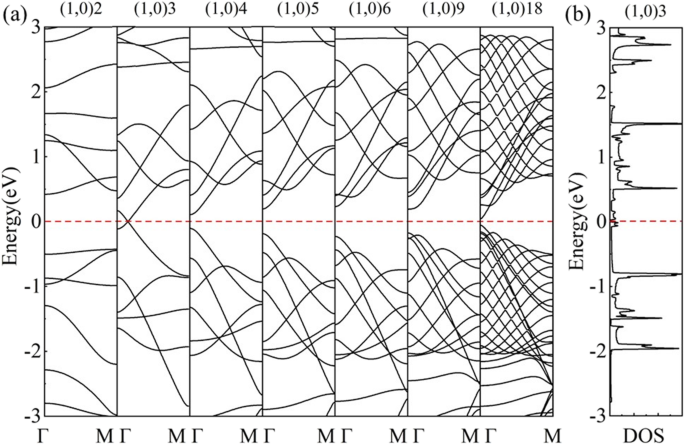
( a ) Evolución de la banda de HOT nanotubos de grafeno (1,0) n ( n = 2, 3, 4, 5, 6, 9, 18); ( b ) DOS del (1,0) 3 nanotubos
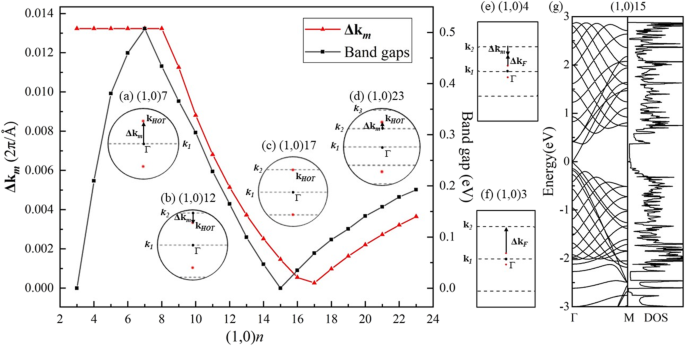
Espacios de banda calculados (línea negra) y distancia Δk m (línea roja) entre k CALIENTE y la k más cercana línea en (1,0) n tubos. Los gráficos insertados son el BZ cerca del punto Γ con k permitido líneas k m ( m =1, 2, 3) (líneas discontinuas) y el punto de Fermi de HOT nanotubos de grafeno k CALIENTE (puntos rojos) en tubo ( a ) (1,0) 7, ( b ) (1,0) 12, ( c ) (1,0) 17, ( d ) (1,0) 23, ( e ) (1,0) 4 y ( f ) (1,0) 3. ( g ) Estructuras de banda y DOS de tubo (1,0) 15
Aunque el Δk m La curva y la curva de banda prohibida tienen similitudes en la forma, las diferencias entre ellas también son obvias, y es que la Δk m el gráfico muestra un "retraso" en el cambio en n ≥ 7 y se vuelve completamente diferente del gráfico de banda prohibida en 3 ≤ n ≤ 7. La razón es que el punto de Fermi en HOT nanotubos de grafeno ( k F ) se supone que tiene la misma coordenada que el punto Fermi original en HOT grafeno ( k CALIENTE ) en la sección anterior donde se explicó el cambio de la banda prohibida. Sin embargo, el punto de Fermi ( k F ) en nanotubos se aleja del punto de origen de Fermi ( k CALIENTE ) en HOT hoja de grafeno bajo el efecto de curvatura. Por lo tanto, la k F desplazamiento (Δ k F = k F - k CALIENTE ) El efecto contribuye a los desajustes entre la distancia Δk m y los huecos de la banda. Como se calcula en el (0,1) n tubos (Fig.6), la k F en (1,0) n Los tubos también se desplazan hacia el exterior BZ hacia el punto simétrico X debajo de la curvatura. Por lo tanto, cuando el k más cercano m se encuentra entre las k CALIENTE y el punto Γ, la distancia Δk m subestima la banda prohibida (p. ej., 17 ≤ n ≤ 24 en la Fig. 9d). De lo contrario, la k más cercana m sentado en el exterior de la k CALIENTE punto, resulta en una sobreestimación de la banda prohibida (por ejemplo, 7 ≤ n ≤ 17 en la Fig. 9b). En pequeños nanotubos (3 ≤ n ≤ 7), la k F el efecto de desplazamiento se mejora bajo la gran tasa de crecimiento de la curvatura; en consecuencia, provoca una drástica k F cambiando y cambia la banda prohibida. Cuando el radio es menor que n =8, la k 1 se convierte en el más cercano al k CALIENTE indica una constante Δk m . Sin embargo, la k F El efecto de cambio es tan fuerte que mueve k F más lejos de k 1 pero más cerca de la k 2 (Figura 9e). La k F efecto de cambio gana la competencia con el k líneas en movimiento y comienza a determinar los espacios de banda desde entonces ( n ≤ 7). La k F sigue cambiando a la k 2 a alta velocidad de modo que la distancia entre k F y k 2 se vuelve cada vez más pequeño. Por lo tanto, de (1,0) 7 a (1,0) 3, la banda prohibida disminuye (Fig. 9). Por fin, el k F se pone al día con k 2 y lo cruza en n =3 (figura 9f). Este cruce de un k línea con la k F da como resultado el punto de Dirac en el tubo (1,0) 3 que da lugar a la semimetalicidad (Fig. 8) como se discutió en las secciones anteriores. Mayor disminución del radio a n =2 abre un espacio de 0,848 eV en el tubo (1,0) 2 (Fig. 8). Esta brecha es muy grande y se considera fuera de las k F esquema de cambio, y por lo tanto no se representa en la Fig. 9. En resumen, existe un mecanismo de competencia entre k línea en movimiento y la k F cambiando en la determinación de los huecos de la banda. La k F cables de efecto de desplazamiento en tubos pequeños (7 ≥ n ≥ 3), mientras que k línea de cables móviles en tubos grandes ( n ≥ 8) donde k F el efecto de cambio se desvanece. La cantidad de k F se estima que el desplazamiento es 0,0015 2π / Å en n =15 y 0.0238 2π / Å en n =3 ya que los espacios de banda son 0 eV donde el k desplazado F el punto está en el k permitido líneas. Puede verse que el k F El desplazamiento es 15,86 veces mayor en un tubo pequeño (tubo (1,0) 3) que en un tubo grande (tubo (1,0) 15).
En CALIENTE grafeno, los átomos de carbono están coordinados en tres partes, por lo que el cuarto electrón de valencia juega un papel clave en su conductividad. La densidad de carga descompuesta de la banda calculada ± 0,15 eV alrededor del nivel de Fermi (Fig. 10) muestra la distribución de los electrones en el cono de Dirac. Only the electrons on the 8–8 bonds (Fig. 10a) have an overlapping and the side view (Fig. 10b) shows that the electrons distribute perpendicularly to the HOT graphene sheet, which indicates that the Dirac cone consists of π states. Therefore, the electron overlapping on the 8–8 bonds (enlarged side view in Fig. 10a) is considered to be localized π states. In big nanotubes such as (0,1)6 (Fig. 10c), the charge density is similar to the HOT graphene sheet showing localized π bonds on 8–8 bonds (enlarged side view in Fig. 10c). As the radius decreases to (0,1)2, whose conductivity transforms to metal (Fig. 6), the 8–8 bonds show several deformations (Fig. 10d). Firstly, these states are no longer symmetric with respect to the tube wall. The overlapping of the π state outside the tube wall breaks apart while the π states inside keep overlapping with each other. Besides the 8–8 π bonds, new π bonds form on 4–8 in (0,1)2. These bonds are similar to the deformed 8–8 bonds:separated π states outside the tube wall and overlapping π states inside the tube wall. Every 4–8 bond connects two 8–8 bonds adjacent to it, forming a delocalized π overlapping inside the tube along the tube axis direction. The enlarged side view in Fig. 10d shows the connection between 4 and 8 and 8–8 bonds as a segment of the whole delocalized bond. Therefore, the metallicity in tube (0,1)2 can be attributed to the delocalized π overlapping in the 4–8 and 8–8 bonds along the tube axis direction which provides a pathway for the electrons to travel along the tube. When the radius keeps decreasing, the conductivity disappears and the (0,1)1 tube becomes a semimetal again (Fig. 6). Different from all the other (0,1) n tubes, the 8–8 overlapping (Fig. 10e) in nanotube (0,1)1 is totally broken up; instead, 4–8 overlapping and 4–6 overlapping plays the major role in the Dirac cones. These two bonds belong to two opposite edges in the same carbon tetragons and are arranged parallel to the tube axis. Furthermore, they are no longer π states. Based on the electronic state analysis, a σ-π hybridization takes place at the Fermi level under such a strong curvature in nanotube (0,1)1. It is verified by the charge density which shows the electron states distribute closely to the bond axis (enlarged side view in Fig. 10e). Strongly modified low-lying σ states are introduced at the Fermi level as discussed in the preceding sections (blue line in Fig. 6). Therefore, the σ-π hybrid states in the 4–8 and 4–6 bonds are considered the reason for the semimetallicity in (0,1)1, which is essentially different from the other semimetallic tubes (0,1) n ( n ≥ 3). In another set of HOT graphene nanotubes, the band gaps show adjustability with different tube radius (Fig. 9). The charge densities also present an evolution with the tube radii in Fig. 11. The band decomposed charge density of tube (1,0)9 in Fig. 11a and b shows the localized π states overlapping in both the VBM and CBM. The VBM is contributed by π states on 6–6 bonds and 8–8 bonds (Fig. 11a). The CBM is contributed by π states on part of 4–8 and 6–8 bonds (Fig. 11b). The 4–6 bonds have no states on both of the VBM and CBM. When the (1,0) n tubes become semimetallic at some specific radii, such as n = 15, the VBM and CBM meet with each other. Band decomposed charge density ± 0.15 eV around the Fermi level of (1,0)15 nanotube show the different distribution of electrons from the semiconductive tubes. More importantly, it exhibits a similar distribution to the semimetallic HOT graphene sheet and (0,1) n tubes. The localized π bond of (1,0)15 only locates on the 8–8 bonds. This redistribution of electron in (1,0) n tubes causes the conductivity change.
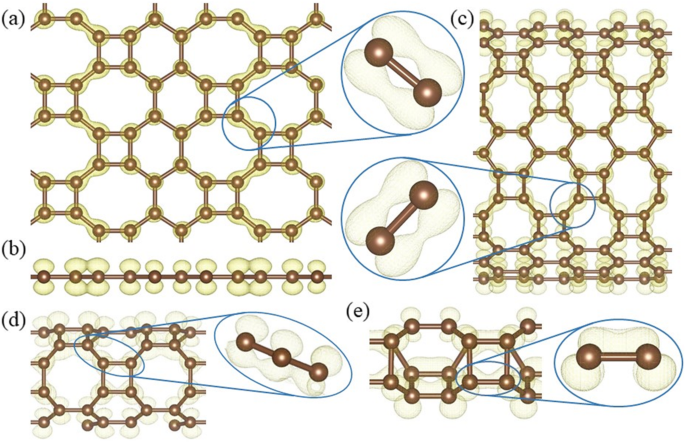
Band decomposed charge densities around the Fermi level of (a ) HOT graphene, (b ) the corresponding side view, and HOT graphene nanotubes (c ) (0,1)6, (d ) (0,1)2, and (e ) (0,1)1 with corresponding enlarged side views
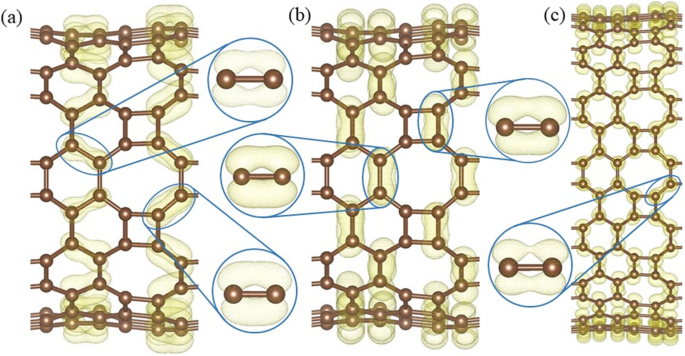
Band decomposed charge densities at (a ) VBM, and (b ) CBM of HOT graphene nanotube (1,0)9; ( c ) charge densities around the Fermi level of the HOT graphene nanotube (1,0)15 with the localized π bond in the enlarged side view
Conclusión
A new graphene allotrope named HOT graphene is constructed by carbon hexagons, octagons, and tetragons showing Dirac cone and high Fermi velocity, which implies that the honeycomb structure is not an indispensable condition for Dirac fermions to exist. The semiconductivity of HOT graphene is dependent on the localized π bonding. A corresponding series of nanotubes is rolled up from the HOT graphene sheet and shows distinctive electronic structures depending on the topology. The set of (0,1) n ( n ≥ 3) HOT graphene nanotubes reveals a character of semimetallicity and Dirac cones that are composed by π states. A non-negligible k F shifting along the allowed k line arises under the curvature effect when the tube radius gets smaller (3 ≤ n ≤ 5). However, the ultra-small nanotube (0,1)2 begins to deviate from the π state-based k F shifting effect showing a transformation to metallicity. Finally, an σ-π hybridization takes the place of the π states at Fermi level in nanotube (0,1)1, where a low-lying σ* band intersection appears at the Fermi level and forms a semimetallicity again. Another set of tubes (1,0) n shows various band gaps (0~ 0.51 eV), which is continuously adjustable with the tube size. The band gaps of (1,0) n ( n ≥ 3) nanotubes turn out to be determined by a competition mechanism between the k line moving and the k F shifting effect. The zone-folding approximation indicates a k line moving and results in the zigzag and periodical band gap changing curve in big tubes (n ≥ 8), while the k F shifting effect gets stronger and causes a dramatic decrease of band gaps in small tubes (7 ≥ n ≥ 3). Zero-gap semimetallic tubes appear periodically under the competition.
Disponibilidad de datos y materiales
Authors declare that the datasets used and/or analyzed during the current study are available to the readers and included in this article.
Abreviaturas
- 1D:
-
One-dimensional
- 2D:
-
Bidimensional
- 3D:
-
Tridimensional
- BZ:
-
Brillouin zone
- CBM:
-
Banda de conducción mínima
- DFT:
-
Teoría funcional de la densidad
- DOS:
-
Densidad de estados
- GGA:
-
Generalized-Gradient Approximation
- HOT :
-
Hexagons, octagons, and tetragons
- PBE:
-
Perdew–Burke–Ernzerh
- VASP:
-
Vienna Ab initio Simulation Package
- VBM:
-
Máximo de banda de valencia
Nanomateriales
- Gestión de memoria C++:nuevo y eliminar
- Nuevas SMU para optimizar la duración de la batería en IoT y semiconductores
- NUEVA FRAMBUESA PI 3 MODELO B + CARACTERÍSTICAS Y COMPRA
- Grafeno en altavoces y auriculares
- Aditivos:los nanotubos de grafeno en los fluoroelastómeros benefician a los sectores del petróleo y gas y de la automoción
- Nylon / Resina PPE modificada para aplicaciones automotrices exigentes en condiciones cálidas y húmedas
- Nuevos robots:económicos y de primera línea
- ¡Noticias! Nueva Fábrica y Oficina
- El nuevo adhesivo CARC tiene mejor rendimiento y es rentable
- BS 4360 Grado 43A Laminado en caliente
- Proceso de laminación en frío y en caliente



