Armónicos en sistemas de energía polifásicos

En el capítulo sobre señales de frecuencia mixta, exploramos el concepto de armónicos en sistemas de CA:frecuencias que son múltiplos enteros de la frecuencia de fuente fundamental.

Con los sistemas de alimentación de CA en los que se supone que la forma de onda de voltaje de la fuente procedente de un generador de CA (alternador) es una onda sinusoidal de frecuencia única, sin distorsiones, no debería haber contenido armónico. . . idealmente.

Componentes no lineales en sistemas de CA

Esto sería cierto si no fuera por los componentes no lineales . Los componentes no lineales consumen corriente de manera desproporcionada con respecto al voltaje de la fuente, lo que genera formas de onda de corriente no sinusoidales.

Ejemplos de componentes no lineales incluyen lámparas de descarga de gas, dispositivos semiconductores de control de potencia (diodos, transistores, SCR, TRIAC), transformadores (la corriente de magnetización del devanado primario generalmente no es sinusoidal debido a la curva de saturación B / H del núcleo) y motores eléctricos (nuevamente, cuando los campos magnéticos dentro del núcleo del motor operan cerca de los niveles de saturación).

Incluso las lámparas incandescentes generan corrientes levemente no sinusoidales, ya que la resistencia del filamento cambia a lo largo del ciclo debido a las rápidas fluctuaciones de temperatura.

Como aprendimos en el capítulo de frecuencias mixtas, cualquier La distorsión de una forma de onda en forma de onda sinusoidal constituye la presencia de frecuencias armónicas.

Cuando la forma de onda no sinusoidal en cuestión es simétrica por encima y por debajo de su línea central promedio, las frecuencias armónicas serán múltiplos enteros impares de la frecuencia de fuente fundamental únicamente, sin múltiplos enteros pares.

La mayoría de las cargas no lineales producen formas de onda de corriente como esta, por lo que los armónicos pares (2º, 4º, 6º, 8º, 10º, 12º, etc.) están ausentes o están mínimamente presentes en la mayoría de los sistemas de alimentación de CA.

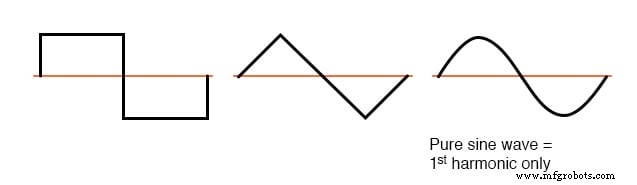
Ejemplos de formas de onda simétricas, solo armónicos impares.

En la figura siguiente se muestran ejemplos de formas de onda asimétricas con armónicos uniformes presentes como referencia.

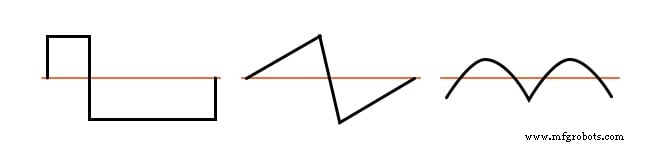
Ejemplos de formas de onda asimétricas, incluso armónicos presentes.

Aunque la mitad de las posibles frecuencias armónicas se eliminan por la distorsión típicamente simétrica de las cargas no lineales, los armónicos impares aún pueden causar problemas. Algunos de estos problemas son generales para todos los sistemas de energía, monofásicos o de otro tipo.

El sobrecalentamiento del transformador debido a pérdidas por corrientes parásitas, por ejemplo, puede ocurrir en cualquier Sistema de alimentación de CA donde hay un contenido armónico significativo.

Sin embargo, existen algunos problemas causados ​​por corrientes armónicas que son específicos de los sistemas de energía polifásicos, y son estos problemas a los que esta sección está específicamente dedicada.

Simulación SPICE sobre efectos armónicos

Es útil poder simular cargas no lineales en SPICE para evitar muchas matemáticas complejas y obtener una comprensión más intuitiva de los efectos armónicos.

Simulación de sistema de CA lineal

Primero, comenzaremos nuestra simulación con un circuito de CA muy simple:una sola fuente de voltaje de onda sinusoidal con una carga puramente lineal y todas las resistencias asociadas:

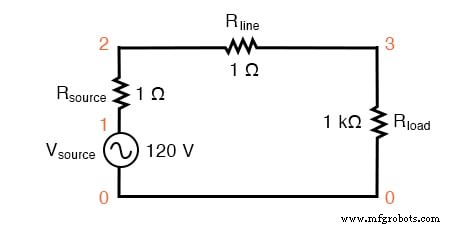
Circuito SPICE con una sola fuente de onda sinusoidal.

La _fuente de R y R _línea Las resistencias en este circuito hacen más que simplemente imitar el mundo real:también proporcionan resistencias de derivación convenientes para medir corrientes en la simulación SPICE:al leer el voltaje a través de una resistencia de 1 Ω, obtiene una indicación directa de la corriente a través de él, ya que E =IR .

Una simulación SPICE de este circuito (listado SPICE:"simulación de carga lineal") con análisis de Fourier del voltaje medido a través de R _línea debería mostrarnos el contenido armónico de la corriente de línea de este circuito. Al ser de naturaleza completamente lineal, no deberíamos esperar ningún otro armónico que el primero (fundamental) de 60 Hz, asumiendo una fuente de 60 Hz.

Consulte el resultado de SPICE "Componentes de Fourier de la respuesta transitoria v (2,3)" y la figura siguiente.

 simulación de carga lineal vsource 1 0 sin (0120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k .opciones itl5 =0 .tran 0.5m 30m 0 1u .plot tran v (2,3) .cuatro 60 v (2,3) .fin 

 Componentes de Fourier de la respuesta transitoria v (2,3) componente dc =4.028E-12 frecuencia armónica normalizada de Fourier fase normalizada sin (hz) componente componente (grados) fase (grados) 1 6.000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 5.793E-12 0.000000 51.122 123.122 3 1.800E + 02 7.407E-12 0.000000 -34.624 37.376 4 2.400E + 02 9.056E-12 0.000000 4.267 76.267 5 3.000E + 02 1.651E-11 0.000000 -83.461 -11.461 6 3.600E + 02 3.931E-11 0.000000 36.399 108.399 7 4.200E + 02 2.338E-11 0.000000 -41.343 30.657 8 4.800E + 02 4.716E-11 0.000000 53.324 125.324 9 5.400E + 02 3.453E-11 0.000000 21.691 93.691 distorsión armónica total =0,000000 por ciento 

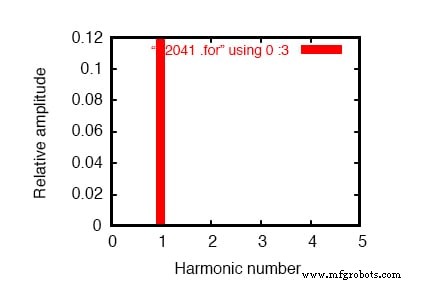
Gráfico de dominio de frecuencia de un componente de frecuencia única. Consulte la lista de SPICE:"simulación de carga lineal".

Aparece un comando .plot en la lista de redes SPICE, y normalmente esto daría como resultado una salida de gráfico de onda sinusoidal. En este caso, sin embargo, he omitido deliberadamente la visualización de la forma de onda por brevedad:el comando .plot está en la lista de conexiones simplemente para satisfacer una peculiaridad de la función de transformación de Fourier de SPICE.

Ninguna transformada discreta de Fourier es perfecta, por lo que vemos que se indican corrientes armónicas muy pequeñas (¡en el rango de pico-amperios!) Para todas las frecuencias hasta el noveno armónico (en la tabla), que es lo más lejos que llega SPICE al realizar el análisis de Fourier. .

Mostramos 0.1198 amperios (1.198E-01) para el "componente de Fourier" del 1er armónico, o la frecuencia fundamental, que es nuestra corriente de carga esperada:aproximadamente 120 mA, dado un voltaje de fuente de 120 voltios y una resistencia de carga de 1 kΩ.

Simulación de sistema de CA monofásico no lineal simple

A continuación, me gustaría simular una carga no lineal para generar corrientes armónicas. Esto se puede hacer de dos formas fundamentalmente diferentes. Una forma es diseñar una carga utilizando componentes no lineales como diodos u otros dispositivos semiconductores que sean fáciles de simular con SPICE. Otra es agregar algunas fuentes de corriente CA en paralelo con la resistencia de carga.

Los ingenieros a menudo prefieren este último método para simular armónicos, ya que las fuentes actuales de valor conocido se prestan mejor al análisis matemático de redes que los componentes con características de respuesta muy complejas.

Dado que estamos dejando que SPICE haga todo el trabajo matemático, la complejidad de un componente semiconductor no nos causaría ningún problema, pero dado que las fuentes de corriente se pueden ajustar para producir cualquier cantidad arbitraria de corriente (una característica conveniente), elija el último enfoque que se muestra en la figura siguiente y en la lista de SPICE "Simulación de carga no lineal".

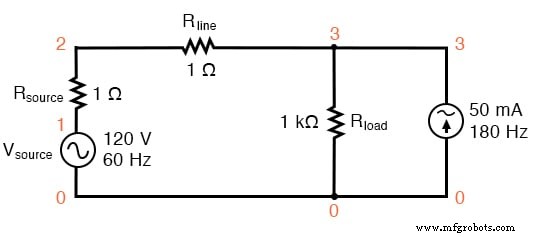
Circuito SPICE:fuente de 60 Hz con tercer armónico agregado.

 Simulación de carga no lineal frente a fuente 1 0 sin (0120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k i3har 3 0 sin (0 50m 180 0 0) .opciones itl5 =0 .tran 0.5m 30m 0 1u .plot tran v (2,3) .cuatro 60 v (2,3) .fin 

En este circuito, tenemos una fuente de corriente de 50 mA de magnitud y una frecuencia de 180 Hz, que es tres veces la frecuencia de la fuente de 60 Hz. Conectado en paralelo con la resistencia de carga de 1 kΩ, su corriente se sumará a la de la resistencia para crear una corriente de línea total no sinusoidal.

Mostraré el gráfico de forma de onda en la figura siguiente solo para que pueda ver los efectos de esta corriente del tercer armónico en la corriente total, que normalmente sería una onda sinusoidal simple.

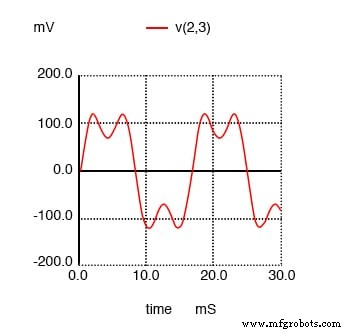
Gráfico de dominio de tiempo de SPICE que muestra la suma de la fuente de 60 Hz y el tercer armónico de 180 Hz.

 Componentes de Fourier de la respuesta transitoria v (2,3) componente dc =1.349E-11 frecuencia armónica normalizada de Fourier fase normalizada sin (hz) componente componente (grados) fase (grados) 1 6.000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 1.609E-11 0.000000 67.570 139.570 3 1.800E + 02 4.990E-02 0.416667 144.000 216.000 4 2.400E + 02 1.074E-10 0.000000 -169.546 -97.546 5 3.000E + 02 3.871E-11 0.000000 169.582 241.582 6 3.600E + 02 5.736E-11 0.000000 140.845 212.845 7 4.200E + 02 8.407E-11 0.000000 177.071 249.071 8 4.800E + 02 1.329E-10 0.000000 156.772 228.772 9 5.400E + 02 2.619E-10 0.000000 160.498 232.498 distorsión armónica total =41,666663 por ciento 

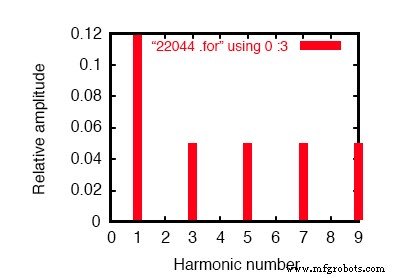
SPICE Diagrama de Fourier que muestra la fuente de 60 Hz y el tercer armónico de 180 Hz.

En el análisis de Fourier, (consulte la figura anterior y “Componentes de Fourier de la respuesta transitoria v (2,3)”) las frecuencias mixtas no se mezclan y se presentan por separado.

Aquí vemos los mismos 0.1198 amperios de corriente (fundamental) de 60 Hz como lo hicimos en la primera simulación, pero apareciendo en la tercera fila armónica vemos 49.9 mA:nuestra fuente de corriente de 50 mA, 180 Hz en el trabajo. ¿Por qué no vemos los 50 mA completos a través de la línea?

Debido a que esa fuente de corriente está conectada a través de la resistencia de carga de 1 kΩ, algunas de sus corrientes se derivan a través de la carga y nunca pasan por la línea de regreso a la fuente. Es una consecuencia inevitable de este tipo de simulación, donde una parte de la carga es "normal" (una resistencia) y la otra parte es imitada por una fuente de corriente.

Simulación de sistema de CA monofásico no lineal con múltiples fuentes de corriente

Si tuviéramos que agregar más fuentes de corriente a la "carga", veríamos una mayor distorsión de la forma de onda de la corriente de línea de la forma de onda sinusoidal ideal, y cada una de esas corrientes armónicas aparecería en el análisis de Fourier. Consulte la figura siguiente y la lista de SPICE:"Simulación de carga no lineal".

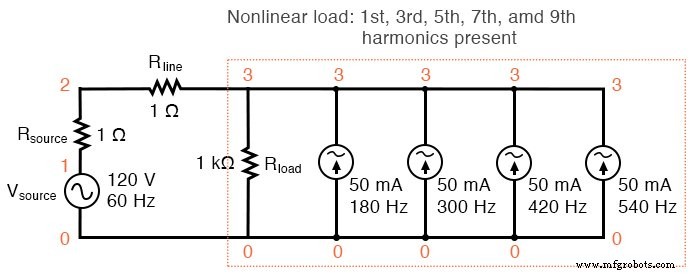
Carga no lineal:1.º, 3.º, 5.º, 7.º y 9.º armónicos presentes.

 simulación de carga no lineal vsource 1 0 sin (0120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k i3har 3 0 sin (0 50m 180 0 0) i5har 3 0 sin (0 50m 300 0 0) i7har 3 0 sin (0 50m 420 0 0) i9har 3 0 sin (0 50m 540 0 0) .opciones itl5 =0 .tran 0.5m 30m 0 1u .plot tran v (2,3) .cuatro 60 v (2,3) .end 

 Componentes de Fourier de la respuesta transitoria v (2,3) componente dc =6.299E-11 frecuencia armónica normalizada de Fourier fase normalizada sin (hz) componente componente (grados) fase (grados) 1 6.000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 1.900E-09 0.000000 -93.908 -21.908 3 1.800E + 02 4.990E-02 0.416667 144.000 216.000 4 2.400E + 02 5.469E-09 0.000000 -116.873 -44.873 5 3.000E + 02 4.990E-02 0.416667 0.000 72.000 6 3.600E + 02 6.271E-09 0.000000 85.062 157.062 7 4.200E + 02 4.990E-02 0.416666 -144.000 -72.000 8 4.800E + 02 2.742E-09 0.000000 -38.781 33.219 9 5.400E + 02 4.990E-02 0.416666 72.000 144.000 distorsión armónica total =83,333296 por ciento 

Análisis de Fourier:"Componentes de Fourier de la respuesta transitoria v (2,3)".

Como puede ver en el análisis de Fourier (Figura anterior), cada fuente de corriente armónica está igualmente representada en la corriente de línea, a 49,9 mA cada una. Hasta ahora, esto es solo una simulación de sistema de energía monofásica.

Simulación de sistema de CA trifásico

Las cosas se ponen más interesantes cuando lo convertimos en una simulación de tres fases. Se realizarán dos análisis de Fourier:uno para el voltaje a través de una resistencia de línea y otro para el voltaje a través de la resistencia neutra.

Como antes, la lectura de voltajes a través de resistencias fijas de 1 Ω cada una proporciona indicaciones directas de la corriente a través de esas resistencias. Consulte la figura siguiente y la lista de SPICE "Sistema de 4 cables de carga / fuente Y-Y con armónicos".

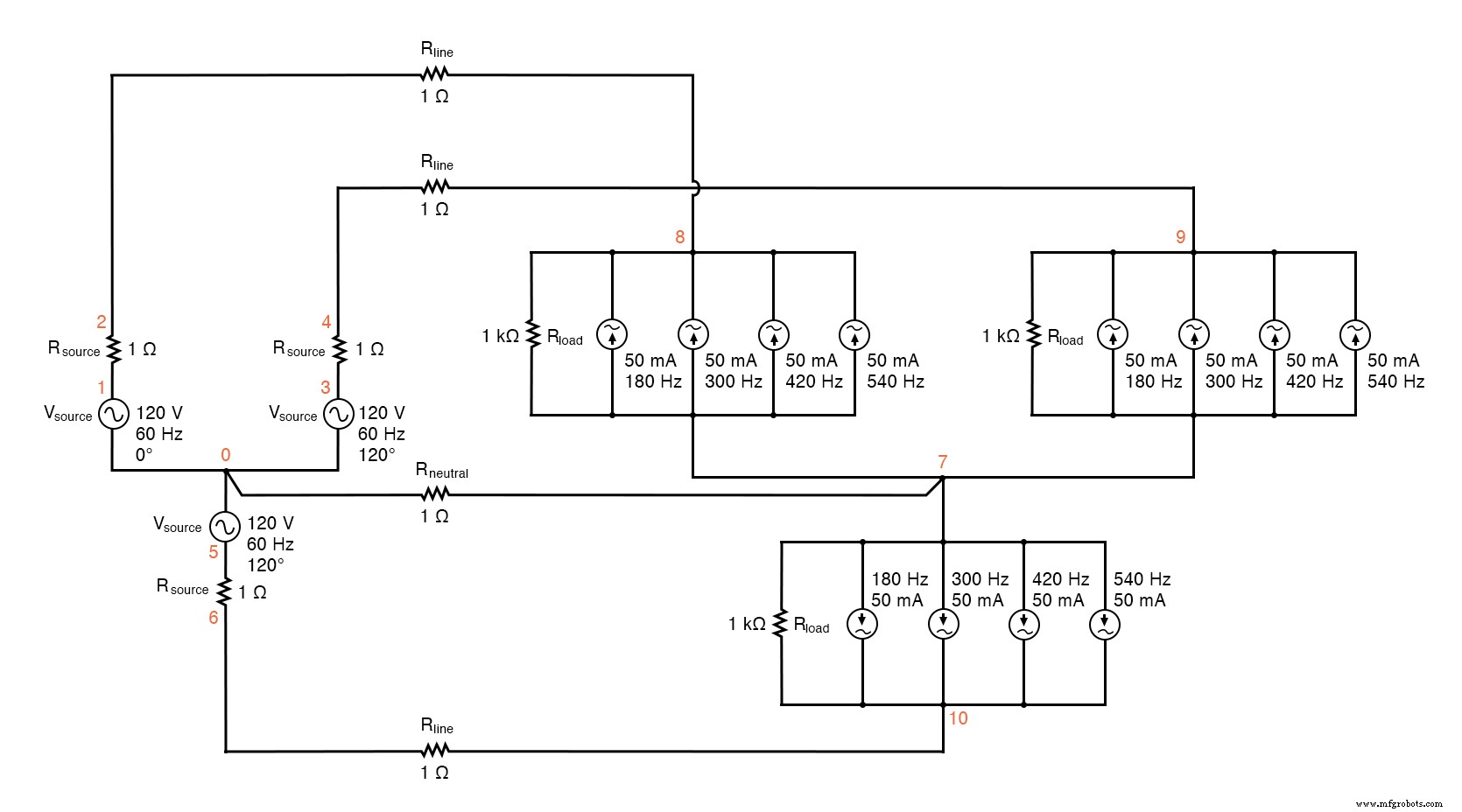
Circuito SPICE:análisis de "corriente de línea" y "corriente neutra", sistema de 4 hilos fuente / carga Y-Y con armónicos.

 Y-Y fuente / carga sistema de 4 hilos con armónicos * * fuente de voltaje fase1 yr (120 v / _ 0 grados) vsource1 1 0 sin (0120 60 0 0) rsource1 1 2 1 * * fuente de voltaje fase2 yr (120 v / _ 120 grados) vsource2 3 0 sin (0120 60 5.55555m 0) rsource2 3 4 1 * * fuente de voltaje fase3 yr (120 v / _ 240 grados) vsource3 5 0 sin (0120 60 11.1111m 0) rsource3 5 6 1 * * resistencias de hilo neutro y de línea rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 rneutral 0 7 1 * * fase 1 de carga rload1 8 7 1k i3har1 8 7 sin (0 50m 180 0 0) i5har1 8 7 sin (0 50m 300 0 0) i7har1 8 7 sin (0 50m 420 0 0) i9har1 8 7 sin (0 50m 540 0 0) * * fase 2 de carga rload2 9 7 1k i3har2 9 7 sin (0 50m 180 5.55555m 0) i5har2 9 7 sin (0 50m 300 5.55555m 0) i7har2 9 7 sin (0 50m 420 5.55555m 0) i9har2 9 7 sin (0 50m 540 5.55555m 0) * * fase 3 de carga rload3 10 7 1k i3har3 10 7 sin (0 50m 180 11.1111m 0) i5har3 10 7 sin (0 50m 300 11.1111m 0) i7har3 10 7 sin (0 50m 420 11.1111m 0) i9har3 10 7 sin (0 50m 540 11.1111m 0) * * material de análisis .opciones itl5 =0 .tran 0.5m 100m 12m 1u .plot tran v (2,8) .cuatro 60 v (2,8) .plot tran v (0,7) .cuatro 60 v (0,7) .fin 

Análisis de Fourier de la corriente de línea:

 Componentes de Fourier de la respuesta transitoria v (2,8) componente de CC =-6.404E-12 frecuencia armónica normalizada de Fourier fase normalizada sin (hz) componente componente (grados) fase (grados) 1 6.000E + 01 1.198E-01 1.000000 0.000 0.000 2 1.200E + 02 2.218E-10 0.000000 172.985 172.985 3 1.800E + 02 4.975E-02 0.415423 0.000 0.000 4 2.400E + 02 4.236E-10 0.000000 166.990 166.990 5 3.000E + 02 4.990E-02 0.416667 0.000 0.000 6 3.600E + 02 1.877E-10 0.000000 -147.146 -147.146 7 4.200E + 02 4.990E-02 0.416666 0.000 0.000 8 4.800E + 02 2.784E-10 0.000000 -148.811 -148.811 9 5.400E + 02 4.975E-02 0.415422 0.000 0.000 distorsión armónica total =83.209009 por ciento 

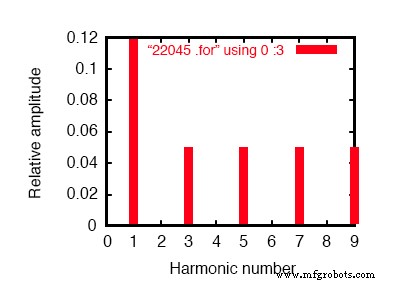
Análisis de Fourier de la corriente de línea en un sistema Y-Y equilibrado.

Análisis de Fourier de la corriente neutra:

 Componentes de Fourier de la respuesta transitoria v (0,7) componente dc =1.819E-10 frecuencia armónica normalizada de Fourier fase normalizada sin (hz) componente componente (grados) fase (grados) 1 6.000E + 01 4.337E-07 1.000000 60.018 0.000 2 1.200E + 02 1.869E-10 0.000431 91.206 31.188 3 1.800E + 02 1.493E-01 344147.7638 -180.000 -240.018 4 2.400E + 02 1.257E-09 0.002898 -21.103 -81.121 5 3.000E + 02 9.023E-07 2.080596 119.981 59.963 6 3.600E + 02 3.396E-10 0.000783 15.882 -44.136 7 4.200E + 02 1.264E-06 2.913955 59.993 -0.025 8 4.800E + 02 5.975E-10 0.001378 35.584 -24.434 9 5.400E + 02 1.493E-01 344147.4889 -179.999 -240.017 

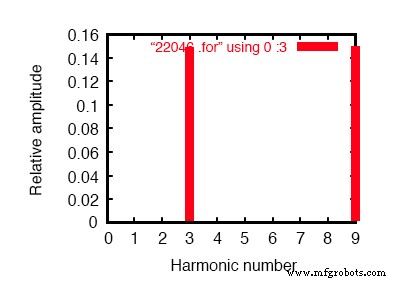
¡El análisis de Fourier de la corriente neutra muestra que no hay armónicos! Compare con la corriente de línea en la Figura anterior.

Este es un sistema de energía balanceado Y-Y, cada fase idéntica al sistema de CA monofásico simulado anteriormente. En consecuencia, no debería sorprender que el análisis de Fourier para la corriente de línea en una fase del sistema trifásico sea casi idéntico al análisis de Fourier para la corriente de línea en el sistema monofásico:una corriente de línea fundamental (60 Hz) de 0.1198 amperios y corrientes armónicas impares de aproximadamente 50 mA cada una.

Consulte la figura anterior y el análisis de Fourier:"Componentes de Fourier de la respuesta transitoria v (2,8)"

Lo que debería sorprender aquí es el análisis de la corriente del conductor neutro, según lo determinado por la caída de voltaje en el R _neutro resistencia entre los nodos SPICE 0 y 7.

En una carga Y trifásica equilibrada, esperaríamos que la corriente neutra fuera cero. Cada corriente de fase, que por sí sola pasaría a través del cable neutro de regreso a la fase de suministro en la fuente Y, debería cancelarse entre sí con respecto al conductor neutro porque todas tienen la misma magnitud y todas están separadas 120 °.

En un sistema sin corrientes armónicas, esto es qué sucede, dejando cero corriente a través del conductor neutro.

Efectos de las corrientes armónicas en el sistema

Sin embargo, no podemos decir lo mismo de armónico corrientes en el mismo sistema.

Tenga en cuenta que la corriente de frecuencia fundamental (60 Hz, o el primer armónico) está prácticamente ausente del conductor neutro. Nuestro análisis de Fourier muestra solo 0,4337 µA del primer armónico cuando se lee el voltaje en R _neutral . Lo mismo puede decirse de los armónicos 5 y 7, teniendo ambas corrientes una magnitud insignificante.

En contraste, los armónicos tercero y noveno están fuertemente representados dentro del conductor neutro, con 149.3 mA (1.493E-01 voltios en 1 Ω) cada uno. Esto es muy cerca de 150 mA, o tres veces los valores de las fuentes de corriente, individualmente.

Con tres fuentes por frecuencia armónica en la carga, parece que nuestras corrientes armónicas 3 y 9 en cada fase están sumando para formar la corriente neutra. Ver análisis de Fourier:"Componentes de Fourier de la respuesta transitoria v (0,7)"

Análisis gráfico en el dominio del tiempo

Esto es exactamente lo que está sucediendo, aunque puede que no sea evidente por qué es así.

La clave para comprender esto se aclara en un gráfico de las corrientes de fase en el dominio del tiempo. Examine este gráfico de corrientes de fase equilibradas a lo largo del tiempo, con una secuencia de fase de 1-2-3. (Figura siguiente)

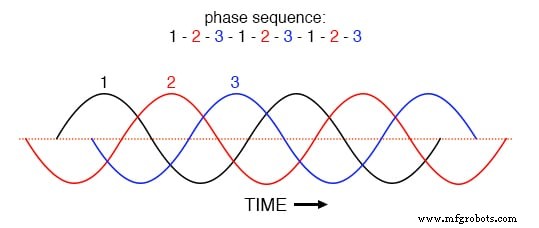
Secuencia de fase 1-2-3-1-2-3-1-2-3 de ondas igualmente espaciadas.

Con las tres formas de onda fundamentales igualmente desplazadas a lo largo del eje de tiempo del gráfico, es fácil ver cómo se cancelarían entre sí para dar una corriente resultante de cero en el conductor neutro. Sin embargo, consideremos cómo se vería una forma de onda del tercer armónico para la fase 1 superpuesta en el gráfico de la siguiente figura.

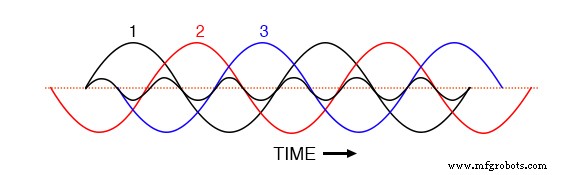
La forma de onda del tercer armónico para la fase 1 superpuesta en formas de onda fundamentales trifásicas.

Observe cómo esta forma de onda armónica tiene la misma relación de fase con la segunda y la tercera forma de onda fundamental que con la primera:en cada semiciclo positivo de cualquiera de las formas de onda fundamentales, encontrará exactamente dos semiciclos positivos y un semiciclo negativo de la forma de onda armónica.

Lo que esto significa es que las formas de onda del tercer armónico de tres formas de onda de frecuencia fundamental con desplazamiento de fase de 120 ° están en realidad en fase juntos. ¡La cifra de desplazamiento de fase de 120 ° generalmente asumida en sistemas de CA trifásicos se aplica solo a las frecuencias fundamentales, no a sus múltiplos armónicos!

Si tuviéramos que trazar las tres formas de onda del tercer armónico en el mismo gráfico, las veríamos superponerse con precisión y aparecer como una forma de onda única y unificada (mostrada en negrita en la (Figura siguiente)

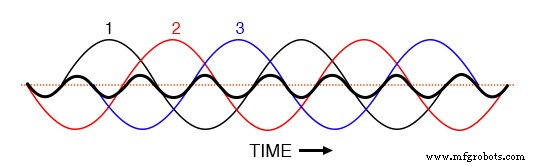
Los terceros armónicos para las fases 1, 2, 3 coinciden todos cuando se superponen a las formas de onda trifásicas fundamentales.

Análisis matemático del gráfico en el dominio del tiempo

Para los más inclinados a las matemáticas, este principio puede expresarse simbólicamente. Suponga que A representa una forma de onda y B otro, ambos a la misma frecuencia, pero desplazados 120 ° entre sí en términos de fase. Llamemos A ’ al tercer armónico de cada forma de onda y B ’ , respectivamente.

El cambio de fase entre A ’ y B ’ no es 120 ° (que es el cambio de fase entre A y B ), pero 3 veces más, porque la A ’ y B ’ las formas de onda se alternan tres veces más rápido que A y B . El cambio entre formas de onda solo se expresa con precisión en términos de ángulo de fase cuando se asume la misma velocidad angular.

Al relacionar formas de onda de diferente frecuencia, la forma más precisa de representar el cambio de fase es en términos de tiempo ; y el time-shift entre A ’ y B ’ es equivalente a 120 ° a una frecuencia tres veces menor, o 360 ° a la frecuencia de A ’ y B ’ . Un cambio de fase de 360 ​​° es lo mismo que un cambio de fase de 0 °, lo que significa que no hay ningún cambio de fase.

Por tanto, A ’ y B ’ deben estar en fase entre sí:

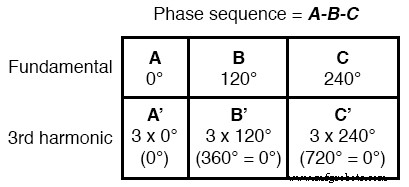
Esta característica del 3er armónico en un sistema trifásico también es válida para cualquier múltiplo entero del 3er armónico.

Entonces, no solo las formas de onda del 3er armónico de cada forma de onda fundamental están en fase entre sí, sino que también lo están los armónicos 6, los armónicos 9, los armónicos 12, los armónicos 15, los armónicos 18, los armónicos 21 y así sucesivamente.

Dado que solo aparecen armónicos impares en sistemas donde la distorsión de la forma de onda es simétrica con respecto a la línea central, y la mayoría de las cargas no lineales crean una distorsión simétrica, los múltiplos pares del 3er armónico (6, 12, 18, etc.) generalmente no son significativos, dejando solo el múltiplos impares (3, 9, 15, 21, etc.) para contribuir significativamente a las corrientes neutrales.

En sistemas de potencia polifásicos con un número de fases distinto de tres, este efecto se produce con armónicos del mismo múltiplo. Por ejemplo, las corrientes armónicas que se agregan al conductor neutro de un sistema de 4 fases conectado en estrella donde el cambio de fase entre las formas de onda fundamentales es de 90 ° serían los 4, 8, 12, 16, 20 y así sucesivamente.

Armónicos triples

Debido a su abundancia e importancia en los sistemas de potencia trifásicos, el 3er armónico y sus múltiplos tienen su propio nombre especial: armónicos triples .

Todos los armónicos triples se suman entre sí en el conductor neutro de una carga conectada en Y de 4 hilos. En los sistemas de energía que contienen una carga no lineal sustancial, las corrientes armónicas triples pueden ser de una magnitud lo suficientemente grande como para provocar el sobrecalentamiento de los conductores neutros.

Esto es muy problemático, ya que otras preocupaciones de seguridad prohíben que los conductores neutros tengan protección contra sobrecorriente y, por lo tanto, no existe ninguna disposición para la interrupción automática de estas altas corrientes.

Análisis de los efectos de los armónicos triples en un circuito Y-Y

La siguiente ilustración muestra cómo las corrientes armónicas triples creadas en la carga se suman dentro del conductor neutro. El símbolo “ω” se usa para representar la velocidad angular y es matemáticamente equivalente a 2πf. Entonces, "ω" representa la frecuencia fundamental, "3ω" representa el tercer armónico, "5ω" representa el quinto armónico, y así sucesivamente:(Figura siguiente)

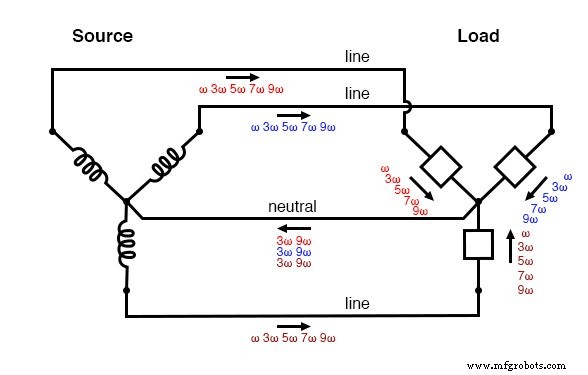
Fuente / carga triple “Y-Y”:las corrientes armónicas se agregan al conductor neutro.

En un esfuerzo por mitigar estas corrientes triples aditivas, uno podría tener la tentación de quitar el cable neutro por completo. Si no hay un cable neutro en el que las corrientes triples puedan fluir juntas, entonces no lo harán, ¿verdad?

Unfortunately, doing so just causes a different problem:the load’s “Y” center-point will no longer be at the same potential as the source’s, meaning that each phase of the load will receive a different voltage than what is produced by the source.

We’ll re-run the last SPICE simulation without the 1 Ω R_neutral resistor and see what happens:

Y-Y source/load (no neutral) with harmonics * * phase1 voltage source and r (120 v / 0 deg) vsource1 1 0 sin(0 120 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v / 120 deg) vsource2 3 0 sin(0 120 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v / 240 deg) vsource3 5 0 sin(0 120 60 11.1111m 0) rsource3 5 6 1 * * line resistances rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 * * phase 1 of load rload1 8 7 1k i3har1 8 7 sin(0 50m 180 0 0) i5har1 8 7 sin(0 50m 300 0 0) i7har1 8 7 sin(0 50m 420 0 0) i9har1 8 7 sin(0 50m 540 0 0) * * phase 2 of load rload2 9 7 1k i3har2 9 7 sin(0 50m 180 5.55555m 0) i5har2 9 7 sin(0 50m 300 5.55555m 0) i7har2 9 7 sin(0 50m 420 5.55555m 0) i9har2 9 7 sin(0 50m 540 5.55555m 0) * * phase 3 of load rload3 10 7 1k i3har3 10 7 sin(0 50m 180 11.1111m 0) i5har3 10 7 sin(0 50m 300 11.1111m 0) i7har3 10 7 sin(0 50m 420 11.1111m 0) i9har3 10 7 sin(0 50m 540 11.1111m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 12m 1u .plot tran v(2,8) .four 60 v(2,8) .plot tran v(0,7) .four 60 v(0,7) .plot tran v(8,7) .four 60 v(8,7) .fin 

Fourier analysis of line current:

Fourier components of transient response v(2,8) dc component =5.423E-11 harmonic frequency Fourier normalized phase normalized sin (hz) componente componente (grados) fase (grados) 1 6.000E+01 1.198E-01 1.000000 0.000 0.000 2 1.200E+02 2.388E-10 0.000000 158.016 158.016 3 1.800E+02 3.136E-07 0.000003 -90.009 -90.009 4 2.400E+02 5.963E-11 0.000000 -111.510 -111.510 5 3.000E+02 4.990E-02 0.416665 0.000 0.000 6 3.600E+02 8.606E-11 0.000000 -124.565 -124.565 7 4.200E+02 4.990E-02 0.416668 0.000 0.000 8 4.800E+02 8.126E-11 0.000000 -159.638 -159.638 9 5.400E+02 9.406E-07 0.000008 -90.005 -90.005 total harmonic distortion =58.925539 percent 

Fourier analysis of voltage between the two “Y” center-points:

Fourier components of transient response v(0,7) dc component =6.093E-08 harmonic frequency Fourier normalized phase normalized sin (hz) componente componente (grados) fase (grados) 1 6.000E+01 1.453E-04 1.000000 60.018 0.000 2 1.200E+02 6.263E-08 0.000431 91.206 31.188 3 1.800E+02 5.000E+01 344147.7879 -180.000 -240.018 4 2.400E+02 4.210E-07 0.002898 -21.103 -81.121 5 3.000E+02 3.023E-04 2.080596 119.981 59.963 6 3.600E+02 1.138E-07 0.000783 15.882 -44.136 7 4.200E+02 4.234E-04 2.913955 59.993 -0.025 8 4.800E+02 2.001E-07 0.001378 35.584 -24.434 9 5.400E+02 5.000E+01 344147.4728 -179.999 -240.017 total harmonic distortion =************ percent 

Fourier analysis of load phase voltage:

Fourier components of transient response v(8,7) dc component =6.070E-08 harmonic frequency Fourier normalized phase normalized sin (hz) componente componente (grados) fase (grados) 1 6.000E+01 1.198E+02 1.000000 0.000 0.000 2 1.200E+02 6.231E-08 0.000000 90.473 90.473 3 1.800E+02 5.000E+01 0.417500 -180.000 -180.000 4 2.400E+02 4.278E-07 0.000000 -19.747 -19.747 5 3.000E+02 9.995E-02 0.000835 179.850 179.850 6 3.600E+02 1.023E-07 0.000000 13.485 13.485 7 4.200E+02 9.959E-02 0.000832 179.790 179.789 8 4.800E+02 1.991E-07 0.000000 35.462 35.462 9 5.400E+02 5.000E+01 0.417499 -179.999 -179.999 total harmonic distortion =59.043467 percent 

Strange things are happening, indeed.

First, we see that the triplen harmonic currents (3rd and 9th) all but disappear in the lines connecting a load to source. The 5th and 7th harmonic currents are present at their normal levels (approximately 50 mA), but the 3rd and 9th harmonic currents are of negligible magnitude.

Second, we see that there is a substantial harmonic voltage between the two “Y” center-points, between which the neutral conductor used to connect. According to SPICE, there are 50 volts of both 3rd and 9th harmonic frequency between these two points, which is definitely not normal in a linear (no harmonics), balanced Y system.

Finally, the voltage as measured across one of the load’s phases (between nodes 8 and 7 in the SPICE analysis) likewise shows strong triplen harmonic voltages of 50 volts each.

The figure below is a graphical summary of the aforementioned effects.

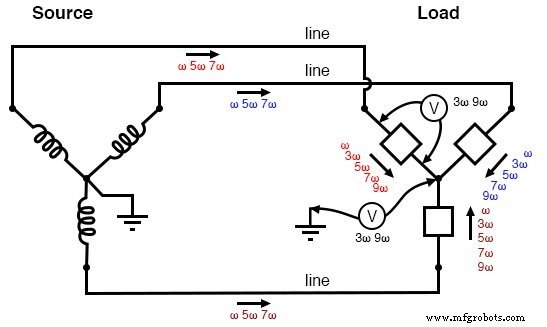
Three-wire “Y-Y” (no neutral) system:Triplen voltages appear between “Y” centers. Triplen voltages appear across load phases. Non-triplen currents appear in line conductors.

In summary, removal of the neutral conductor leads to a “hot” center-point on the load “Y”, and also to harmonic load phase voltages of equal magnitude, all comprised of triplen frequencies.

In the previous simulation where we had a 4-wire, Y-connected system, the undesirable effect from harmonics was excessive neutral current , but at least each phase of the load received voltage nearly free of harmonics.

Analysis of the Effects of Triplen Harmonics in a Delta-Wye(Y) Circuit

Since removing the neutral wire didn’t seem to work in eliminating the problems caused by harmonics, perhaps switching to a Δ configuration will. Let’s try a Δ source instead of a Y, keeping the load in its present Y configuration, and see what happens.

The measured parameters will be line current (voltage across R_line , nodes 0 and 8), load phase voltage (nodes 8 and 7), and source phase current (voltage across R_source , nodes 1 and 2). (Figura siguiente)

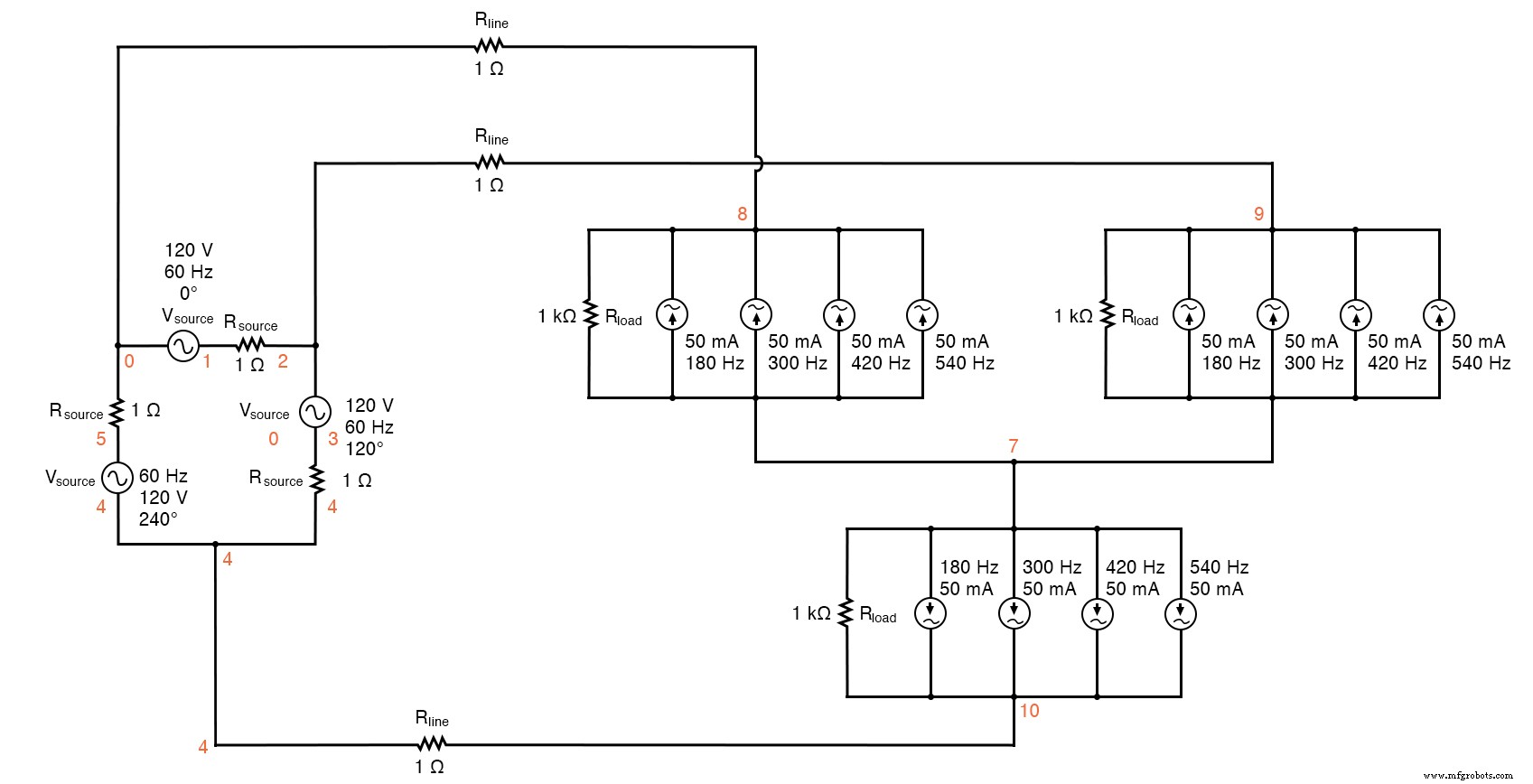
Delta-Y source/load with harmonics

Delta-Y source/load with harmonics * * phase1 voltage source and r (120 v /_ 0 deg) vsource1 1 0 sin(0 207.846 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v /_ 120 deg) vsource2 3 2 sin(0 207.846 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v /_ 240 deg) vsource3 5 4 sin(0 207.846 60 11.1111m 0) rsource3 5 0 1 * * line resistances rline1 0 8 1 rline2 2 9 1 rline3 4 10 1 * * phase 1 of load rload1 8 7 1k i3har1 8 7 sin(0 50m 180 9.72222m 0) i5har1 8 7 sin(0 50m 300 9.72222m 0) i7har1 8 7 sin(0 50m 420 9.72222m 0) i9har1 8 7 sin(0 50m 540 9.72222m 0) * * phase 2 of load rload2 9 7 1k i3har2 9 7 sin(0 50m 180 15.2777m 0) i5har2 9 7 sin(0 50m 300 15.2777m 0) i7har2 9 7 sin(0 50m 420 15.2777m 0) i9har2 9 7 sin(0 50m 540 15.2777m 0) * * phase 3 of load rload3 10 7 1k i3har3 10 7 sin(0 50m 180 4.16666m 0) i5har3 10 7 sin(0 50m 300 4.16666m 0) i7har3 10 7 sin(0 50m 420 4.16666m 0) i9har3 10 7 sin(0 50m 540 4.16666m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 16m 1u .plot tran v(0,8) v(8,7) v(1,2) .four 60 v(0,8) v(8,7) v(1,2) .fin 

Note:the following paragraph is for those curious readers who follow every detail of my SPICE netlists. If you just want to find out what happens in the circuit, skip this paragraph!

When simulating circuits having AC sources of differing frequency and differing phase, the only way to do it in SPICE is to set up the sources with a delay time or phase offset specified in seconds. Thus, the 0° source has these five specifying figures:“(0 207.846 60 0 0)”, which means 0 volts DC offset, 207.846 volts peak amplitude (120 times the square root of three, to ensure the load phase voltages remain at 120 volts each), 60 Hz, 0 time delay, and 0 damping factor.

The 120° phase-shifted source has these figures:“(0 207.846 60 5.55555m 0)”, all the same as the first except for the time delay factor of 5.55555 milliseconds, or 1/3 of the full period of 16.6667 milliseconds for a 60 Hz waveform.

The 240° source must be time-delayed twice that amount, equivalent to a fraction of 240/360 of 16.6667 milliseconds, or 11.1111 milliseconds.

This is for the Δ-connected source. The Y-connected load, on the other hand, requires a different set of time-delay figures for its harmonic current sources, because the phase voltages in a Y load are not in phase with the phase voltages of a Δ source.

If Δ source voltages VAC, VBA, and VCB are referenced at 0°, 120°, and 240°, respectively, then “Y” load voltages VA, VB, and VC will have phase angles of -30°, 90°, and 210°, respectively.

This is an intrinsic property of all Δ-Y circuits and not a quirk of SPICE. Therefore, when I specified the delay times for the harmonic sources, I had to set them at 15.2777 milliseconds (-30°, or +330°), 4.16666 milliseconds (90°), and 9.72222 milliseconds (210°).

One final note:when delaying AC sources in SPICE, they don’t “turn on” until their delay time has elapsed, which means any mathematical analysis up to that point in time will be in error. Consequently, I set the .tran transient analysis line to hold off analysis until 16 milliseconds after the start, which gives all sources in the netlist time to engage before any analysis takes place.

The result of this analysis is almost as disappointing as the last. (Figure below) Line currents remain unchanged (the only substantial harmonic content being the 5th and 7th harmonics), and load phase voltages remain unchanged as well, with a full 50 volts of triplen harmonic (3rd and 9th) frequencies across each load component.

Source phase current is a fraction of the line current, which should come as no surprise. Both 5th and 7th harmonics are represented there, with negligible triplen harmonics:

Fourier analysis of line current:

 Fourier components of transient response v(0,8) dc component =-6.850E-11 harmonic frequency Fourier normalized phase normalized sin (hz) componente componente (grados) fase (grados) 1 6.000E+01 1.198E-01 1.000000 150.000 0.000 2 1.200E+02 2.491E-11 0.000000 159.723 9.722 3 1.800E+02 1.506E-06 0.000013 0.005 -149.996 4 2.400E+02 2.033E-11 0.000000 52.772 -97.228 5 3.000E+02 4.994E-02 0.416682 30.002 -119.998 6 3.600E+02 1.234E-11 0.000000 57.802 -92.198 7 4.200E+02 4.993E-02 0.416644 -29.998 -179.998 8 4.800E+02 8.024E-11 0.000000 -174.200 -324.200 9 5.400E+02 4.518E-06 0.000038 -179.995 -329.995 total harmonic distortion =58.925038 percent 

Fourier analysis of load phase voltage:

Fourier components of transient response v(8,7) dc component =1.259E-08 harmonic frequency Fourier normalized phase normalized sin (hz) componente componente (grados) fase (grados) 1 6.000E+01 1.198E+02 1.000000 150.000 0.000 2 1.200E+02 1.941E-07 0.000000 49.693 -100.307 3 1.800E+02 5.000E+01 0.417222 -89.998 -239.998 4 2.400E+02 1.519E-07 0.000000 66.397 -83.603 5 3.000E+02 6.466E-02 0.000540 -151.112 -301.112 6 3.600E+02 2.433E-07 0.000000 68.162 -81.838 7 4.200E+02 6.931E-02 0.000578 148.548 -1.453 8 4.800E+02 2.398E-07 0.000000 -174.897 -324.897 9 5.400E+02 5.000E+01 0.417221 90.006 -59.995 total harmonic distortion =59.004109 percent 

Fourier analysis of source phase current:

Fourier components of transient response v(1,2) dc component =3.564E-11 harmonic frequency Fourier normalized phase normalized sin (hz) componente componente (grados) fase (grados) 1 6.000E+01 6.906E-02 1.000000 -0.181 0.000 2 1.200E+02 1.525E-11 0.000000 -156.674 -156.493 3 1.800E+02 1.422E-06 0.000021 -179.996 -179.815 4 2.400E+02 2.949E-11 0.000000 -110.570 -110.390 5 3.000E+02 2.883E-02 0.417440 -179.996 -179.815 6 3.600E+02 2.324E-11 0.000000 -91.926 -91.745 7 4.200E+02 2.883E-02 0.417398 -179.994 -179.813 8 4.800E+02 4.140E-11 0.000000 -39.875 -39.694 9 5.400E+02 4.267E-06 0.000062 0.006 0.186 total harmonic distortion =59.031969 percent 

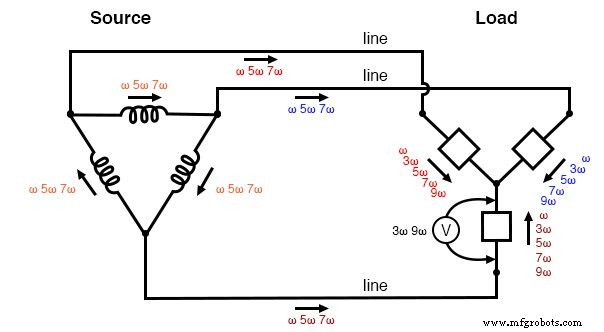
“Δ-Y” source/load:Triplen voltages appear across load phases. Non-triplen currents appear in line conductors and in source phase windings.

Really, the only advantage of the Δ-Y configuration from the standpoint of harmonics is that there is no longer a center-point at the load posing a shock hazard. Otherwise, the load components receive the same harmonically-rich voltages and the lines see the same currents as in a three-wire Y system.

Analysis of the Effects of Triplen Harmonics in a Delta - Delta Circuit

If we were to reconfigure the system into a Δ-Δ arrangement, (Figure below) that should guarantee that each load component receives non-harmonic voltage, since each load phase would be directly connected in parallel with each source phase.

The complete lack of any neutral wires or “center points” in a Δ-Δ system prevents strange voltages or additive currents from occurring.

It would seem to be the ideal solution. Let’s simulate and observe, analyzing line current, load phase voltage, and source phase current. See SPICE listing:“Delta-Delta source/load with harmonics”, “Fourier analysis:Fourier components of transient response v(0,6)”, and “Fourier components of transient response v(2,1)”.

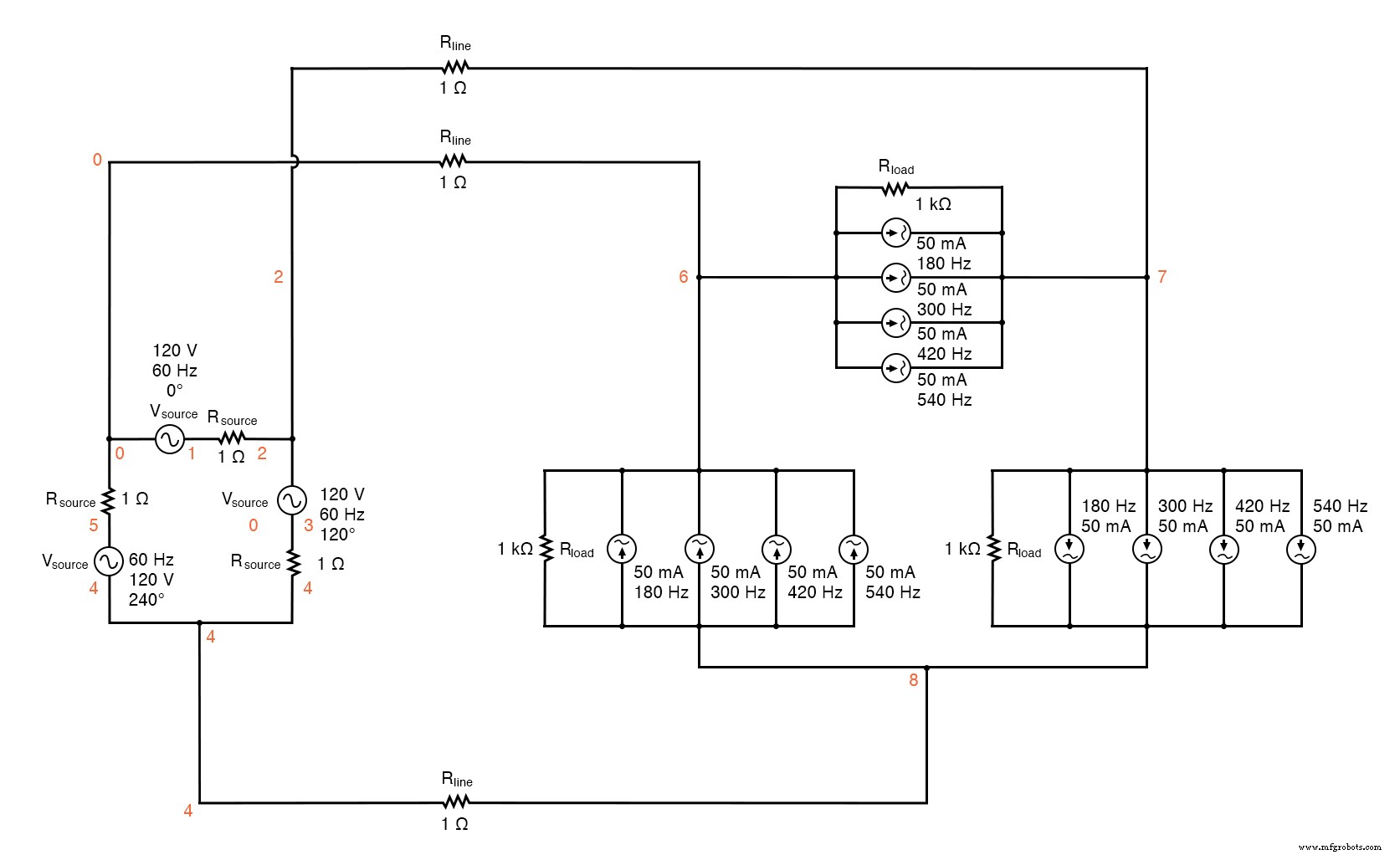
Delta-Delta source/load with harmonics.

Delta-Delta source/load with harmonics * * phase1 voltage source and r (120 v /_ 0 deg) vsource1 1 0 sin(0 120 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v /_ 120 deg) vsource2 3 2 sin(0 120 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v /_ 240 deg) vsource3 5 4 sin(0 120 60 11.1111m 0) rsource3 5 0 1 * * line resistances rline1 0 6 1 rline2 2 7 1 rline3 4 8 1 * * phase 1 of load rload1 7 6 1k i3har1 7 6 sin(0 50m 180 0 0) i5har1 7 6 sin(0 50m 300 0 0) i7har1 7 6 sin(0 50m 420 0 0) i9har1 7 6 sin(0 50m 540 0 0) * * phase 2 of load rload2 8 7 1k i3har2 8 7 sin(0 50m 180 5.55555m 0) i5har2 8 7 sin(0 50m 300 5.55555m 0) i7har2 8 7 sin(0 50m 420 5.55555m 0) i9har2 8 7 sin(0 50m 540 5.55555m 0) * * phase 3 of load rload3 6 8 1k i3har3 6 8 sin(0 50m 180 11.1111m 0) i5har3 6 8 sin(0 50m 300 11.1111m 0) i7har3 6 8 sin(0 50m 420 11.1111m 0) i9har3 6 8 sin(0 50m 540 11.1111m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 16m 1u .plot tran v(0,6) v(7,6) v(2,1) i(3har1) .four 60 v(0,6) v(7,6) v(2,1) .fin 

Fourier analysis of line current:

Fourier components of transient response v(0,6) dc component =-6.007E-11 harmonic frequency Fourier normalized phase normalized sin (hz) componente componente (grados) fase (grados) 1 6.000E+01 2.070E-01 1.000000 150.000 0.000 2 1.200E+02 5.480E-11 0.000000 156.666 6.666 3 1.800E+02 6.257E-07 0.000003 89.990 -60.010 4 2.400E+02 4.911E-11 0.000000 8.187 -141.813 5 3.000E+02 8.626E-02 0.416664 -149.999 -300.000 6 3.600E+02 1.089E-10 0.000000 -31.997 -181.997 7 4.200E+02 8.626E-02 0.416669 150.001 0.001 8 4.800E+02 1.578E-10 0.000000 -63.940 -213.940 9 5.400E+02 1.877E-06 0.000009 89.987 -60.013 total harmonic distortion =58.925538 percent 

Fourier analysis of load phase voltage:

Fourier components of transient response v(7,6) dc component =-5.680E-10 harmonic frequency Fourier normalized phase normalized sin (hz) componente componente (grados) fase (grados) 1 6.000E+01 1.195E+02 1.000000 0.000 0.000 2 1.200E+02 1.039E-09 0.000000 144.749 144.749 3 1.800E+02 1.251E-06 0.000000 89.974 89.974 4 2.400E+02 4.215E-10 0.000000 36.127 36.127 5 3.000E+02 1.992E-01 0.001667 -180.000 -180.000 6 3.600E+02 2.499E-09 0.000000 -4.760 -4.760 7 4.200E+02 1.992E-01 0.001667 -180.000 -180.000 8 4.800E+02 2.951E-09 0.000000 -151.385 -151.385 9 5.400E+02 3.752E-06 0.000000 89.905 89.905 total harmonic distortion =0.235702 percent 

Fourier analysis of source phase current:

Fourier components of transient response v(2,1) dc component =-1.923E-12 harmonic frequency Fourier normalized phase normalized sin (hz) componente componente (grados) fase (grados) 1 6.000E+01 1.194E-01 1.000000 179.940 0.000 2 1.200E+02 2.569E-11 0.000000 133.491 -46.449 3 1.800E+02 3.129E-07 0.000003 89.985 -89.955 4 2.400E+02 2.657E-11 0.000000 23.368 -156.571 5 3.000E+02 4.980E-02 0.416918 -180.000 -359.939 6 3.600E+02 4.595E-11 0.000000 -22.475 -202.415 7 4.200E+02 4.980E-02 0.416921 -180.000 -359.939 8 4.800E+02 7.385E-11 0.000000 -63.759 -243.699 9 5.400E+02 9.385E-07 0.000008 89.991 -89.949 total harmonic distortion =58.961298 percent 

As predicted earlier, the load phase voltage is almost a pure sine-wave, with negligible harmonic content, thanks to the direct connection with the source phases in a Δ-Δ system.

But what happened to the triplen harmonics? The 3rd and 9th harmonic frequencies don’t appear in any substantial amount in the line current, nor in the load phase voltage, nor in the source phase current! We know that triplen currents exist because the 3rd and 9th harmonic current sources are intentionally placed in the phases of the load, but where did those currents go?

Analysis of the Effects of Triplen Harmonics in a Delta - Delta Circuit

Remember that the triplen harmonics of 120° phase-shifted fundamental frequencies are in phase with each other.

Note the directions that the arrows of the current sources within the load phases are pointing, and think about what would happen if the 3rd and 9th harmonic sources were DC sources instead.

What we would have is currently circulating within the loop formed by the Δ-connected phases . This is where the triplen harmonic currents have gone:they stay within the Δ of the load, never reaching the line conductors or the windings of the source.

These results may be graphically summarized as such in the figure below.

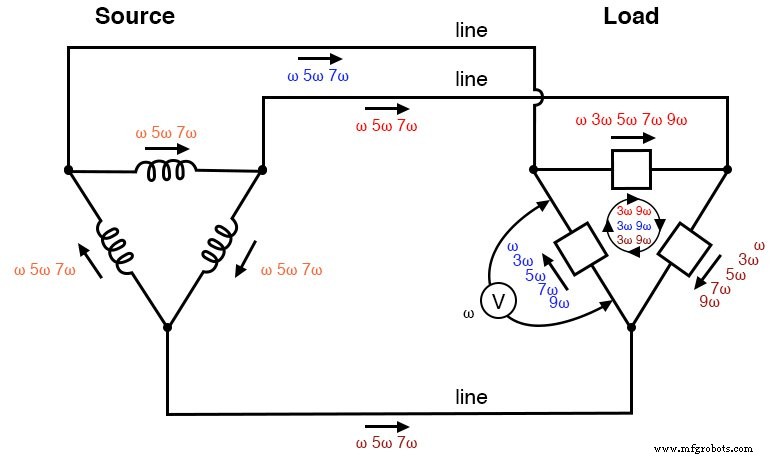
Δ-Δ source/load:Load phases receive undistorted sine wave voltages. Triplen currents are confined to circulate within load phases. Non-triplen currents appear in line conductors and in source phase windings.

This is a major benefit of the Δ-Δ system configuration:triplen harmonic currents remain confined in whatever set of components create them and do not “spread” to other parts of the system.

REVISAR:

• Nonlinear components are those that draw a non-sinusoidal (non-sine-wave) current waveform when energized by a sinusoidal (sine-wave) voltage. Since any distortion of an originally pure sine-wave constitutes harmonic frequencies, we can say that nonlinear components generate harmonic currents.
• When the sine-wave distortion is symmetrical above and below the average centerline of the waveform, the only harmonics present will be odd-numbered , not even-numbered.
• The 3rd harmonic, and integer multiples of it (6th, 9th, 12th, 15th) are known as triplen harmonics. They are in phase with each other, despite the fact that their respective fundamental waveforms are 120° out of phase with each other.
• In a 4-wire Y-Y system, triplen harmonic currents add within the neutral conductor.
• Triplen harmonic currents in a Δ-connected set of components circulate within the loop formed by the Δ.

HOJAS DE TRABAJO RELACIONADAS:

• Mixed-Frequency Signals Worksheet