Funciones de lógica digital

Podemos construir funciones lógicas simples para nuestro circuito hipotético de lámpara, usando múltiples contactos, y documentar estos circuitos de manera bastante fácil y comprensible con peldaños adicionales a nuestra "escalera" original.

Si usamos notación binaria estándar para el estado de los interruptores y la lámpara (0 para no activados o desactivados; 1 para activados o activados), se puede hacer una tabla de verdad para mostrar cómo funciona la lógica:

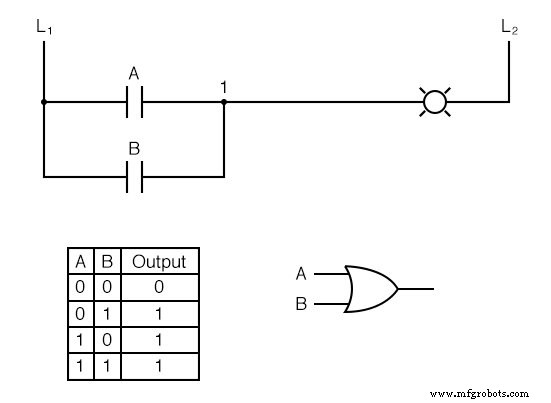
Ahora, la lámpara se encenderá si se activa el contacto A o el contacto B, porque todo lo que se necesita para que la lámpara se energice es tener al menos una ruta para la corriente desde el cable L ₁ al cable 1.

Lo que tenemos es una función lógica OR simple, implementada con nada más que contactos y una lámpara.

Podemos imitar la función lógica AND conectando los dos contactos en serie en lugar de en paralelo:

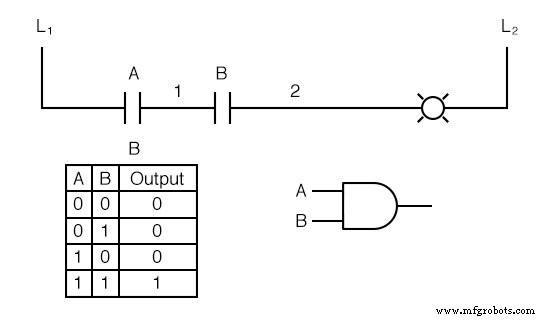
Ahora, la lámpara se energiza solo si contacta A y el contacto B se accionan simultáneamente.

Existe una ruta para la corriente del cable L ₁ a la lámpara (cable 2) si y solo si ambos los contactos del interruptor están cerrados.

La función de inversión lógica, o NO, se puede realizar en una entrada de contacto simplemente usando un contacto normalmente cerrado en lugar de un contacto normalmente abierto:

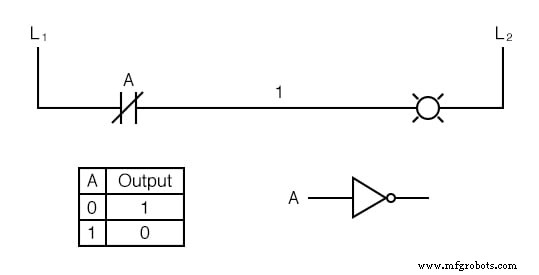
Ahora, la lámpara se energiza si el contacto no accionado, y se desenergiza cuando se acciona el contacto.

Si tomamos nuestra función OR e invertimos cada "entrada" mediante el uso de contactos normalmente cerrados, terminaremos con una función NAND.

En una rama especial de las matemáticas conocida como álgebra booleana , este efecto del cambio de identidad de la función de puerta con la inversión de las señales de entrada se describe en el Teorema de DeMorgan , un tema que se explorará con más detalle en un capítulo posterior.

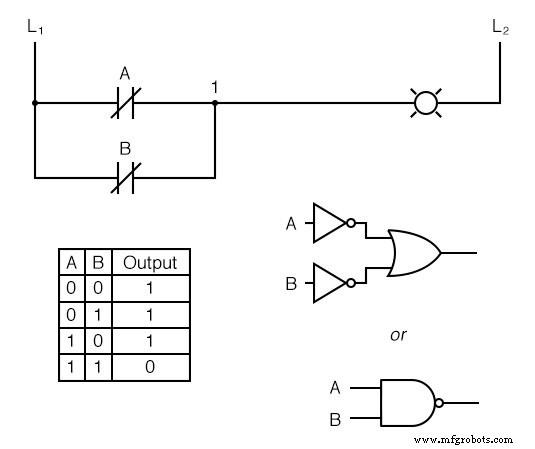
La lámpara se energizará si o el contacto no está activado. Saldrá solo si ambos los contactos se activan simultáneamente.

Del mismo modo, si tomamos nuestra función AND e invertimos cada "entrada" mediante el uso de contactos normalmente cerrados, terminaremos con una función NOR:

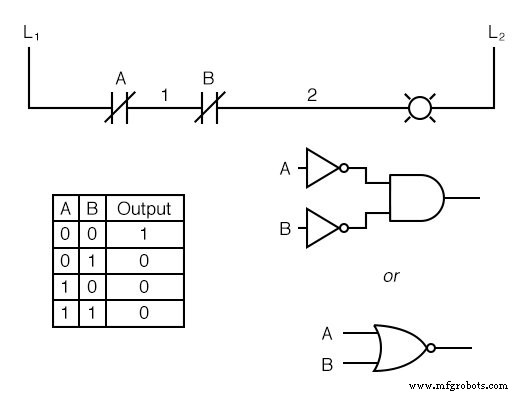
Un patrón se revela rápidamente cuando los circuitos de escalera se comparan con sus contrapartes de puertas lógicas:

• Los contactos paralelos son equivalentes a una puerta OR.
• Los contactos en serie son equivalentes a una puerta AND.
• Los contactos normalmente cerrados son equivalentes a una puerta NOT (inversor).

También podemos construir funciones lógicas combinacionales agrupando contactos en arreglos en serie-paralelo. En el siguiente ejemplo, tenemos una función O exclusiva construida a partir de una combinación de puertas AND, OR y de inversor (NOT):

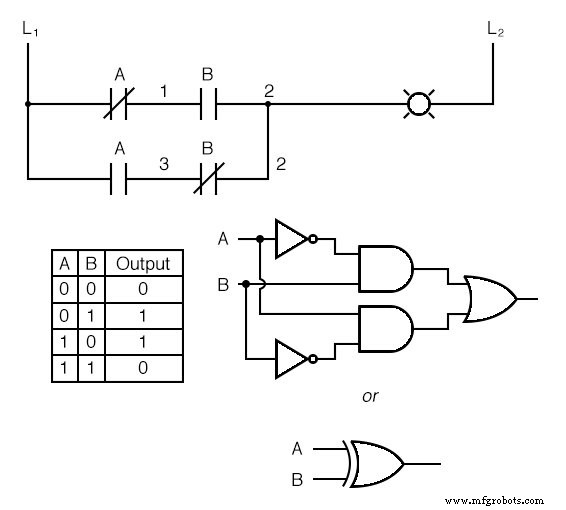
El peldaño superior (contacto NC A en serie con contacto NA B) es el equivalente a la combinación de puerta superior NO / Y.

El peldaño inferior (contacto NA A en serie con contacto NC B) es el equivalente a la combinación de puerta NO / Y inferior.

La conexión en paralelo entre los dos peldaños en el cable número 2 forma el equivalente de la puerta OR, al permitir que el peldaño 1 o el peldaño 2 energicen la lámpara.

Diseño de una función OR exclusiva

Para hacer la función O-Exclusiva, tuvimos que usar dos contactos por entrada:uno para entrada directa y el otro para entrada "invertida".

Los dos contactos "A" se activan físicamente mediante el mismo mecanismo, al igual que los dos contactos "B".

La asociación común entre contactos se indica mediante la etiqueta del contacto.

No hay límite para la cantidad de contactos por interruptor que se pueden representar en un diagrama de escalera, ya que cada nuevo contacto en cualquier interruptor o relé (ya sea normalmente abierto o normalmente cerrado) usado en el diagrama simplemente se marca con la misma etiqueta.

A veces, varios contactos en un solo interruptor (o relé) se designan con etiquetas compuestas, como "A-1" y "A-2" en lugar de dos etiquetas "A".

Esto puede ser especialmente útil si desea designar específicamente qué conjunto de contactos en cada interruptor o relé se está utilizando para qué parte de un circuito.

En aras de la simplicidad, me abstendré de un etiquetado tan elaborado en esta lección. Si ve una etiqueta común para varios contactos, sabrá que todos esos contactos están activados por el mismo mecanismo.

Si deseamos invertir la salida de cualquier función lógica generada por interruptor, debemos usar un relé con un contacto normalmente cerrado.

Por ejemplo, si queremos energizar una carga en función de la inversa, o NO, de un contacto normalmente abierto, podríamos hacer esto:

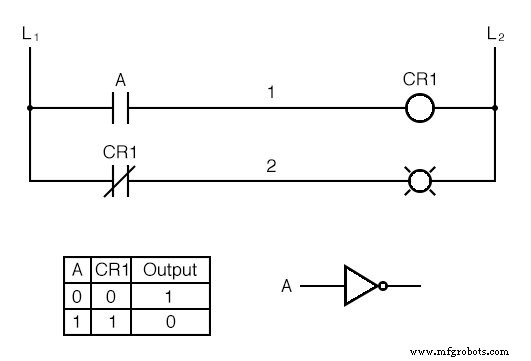
Llamaremos al relé, "relé de control 1" o CR ₁ . Cuando la bobina de CR ₁ (simbolizado con el par de paréntesis en el primer escalón) está energizado, el contacto en el segundo escalón se abre , desenergizando así la lámpara.

Desde el interruptor A a la bobina de CR ₁ , la función lógica no está invertida. El contacto normalmente cerrado accionado por la bobina de relé CR ₁ proporciona una función de inversor lógico para conducir la lámpara en sentido opuesto al estado de activación del interruptor.

Aplicando esta estrategia de inversión a una de nuestras funciones de entrada invertida creadas anteriormente, como OR-a-NAND, podemos invertir la salida con un relé para crear una función no invertida:

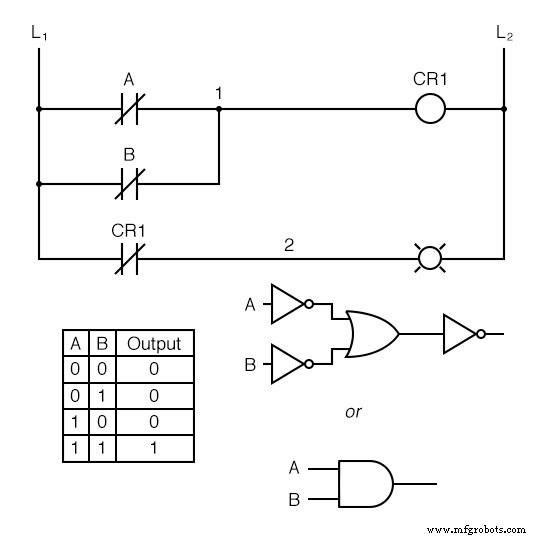
De los interruptores a la bobina de CR ₁ , la función lógica es la de una puerta NAND. CR ₁ El contacto normalmente cerrado proporciona una inversión final para convertir la función NAND en una función AND.

REVISAR :

• Los contactos paralelos son lógicamente equivalentes a una puerta OR.
• Los contactos de la serie son lógicamente equivalentes a una puerta AND.
• Los contactos normalmente cerrados (N.C.) son lógicamente equivalentes a una puerta NOT.
• Se debe usar un relé para invertir la salida de una función de puerta lógica, mientras que los contactos simples del interruptor normalmente cerrados son suficientes para representar las entradas de la puerta invertida .

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de álgebra booleana
• Hoja de trabajo de lógica de relé electromecánico
• Hoja de trabajo de señales lógicas digitales