Influencia de las dislocaciones en el índice de refracción de AlN por campo de deformación a nanoescala

Resumen

El índice de refracción de AlN tiene una influencia directa en los dispositivos optoelectrónicos ultravioleta profundos basados en AlGaN, como la eficiencia cuántica externa de los dispositivos emisores de luz. Revelar la dependencia del índice de refracción de AlN en las dislocaciones de roscado es significativo ya que las dislocaciones de rosca de alta densidad suelen existir en AlN. En este artículo, se investiga el efecto de diferentes densidades de dislocación sobre el índice de refracción de AlN. Con el aumento de las densidades de dislocación de 4,24 × 10 ⁸ a 3,48 × 10 ⁹ cm ^{- 2} , el índice de refracción de AlN disminuye de 2.2508 a 2.2102 a 280 nm. Un estudio adicional demuestra que el campo de deformación a nanoescala alrededor de las dislocaciones cambia la propagación de la luz y, por lo tanto, disminuye el índice de refracción de AlN. Este estudio será beneficioso para el diseño de dispositivos optoelectrónicos y, por lo tanto, la realización de dispositivos optoelectrónicos ultravioleta profunda de alto rendimiento.

Introducción

Los materiales basados en AlN son materiales prometedores para fabricar dispositivos optoelectrónicos ultravioleta profunda (DUV) como diodos emisores de luz (LED) [1,2,3,4,5], diodos láser [6,7,8] y fotodetectores [ 9, 10] debido a la banda prohibida directa sintonizable de 3,4 a 6,2 eV [11]. El índice de refracción de AlN tiene efectos sobre el rendimiento de los dispositivos optoelectrónicos directamente. Para los LED, el índice de refracción de AlN tiene un impacto en la eficiencia de extracción de luz (LEE) porque el ángulo de reflexión interno total está determinado por la diferencia del índice de refracción entre la capa de AlN y otra región, que es el factor limitante clave para la cantidad de salida de luz. Dado que la eficiencia cuántica externa (EQE) es el producto de la eficiencia cuántica interna y el LEE, el índice de refracción de AlN afectará la EQE de los LED. Además, el índice de refracción juega un papel clave en el diseño de estructuras de guías de ondas como el reflector de Bragg distribuido (DBR) [12,13,14], cuya reflectividad es sensible al índice de refracción. Por lo tanto, es importante revelar los factores que afectan el índice de refracción de AlN. Se puede aprender de estudios anteriores que el índice de refracción de AlN puede verse afectado por muchos factores, como la temperatura, la presión y la banda prohibida. El índice de refracción de AlN aumenta con una temperatura más alta [15] y una presión más baja [16]. Para el material a base de AlN, el índice de refracción se reduce con el aumento de la banda prohibida [17]. Además, las dislocaciones en los semiconductores tienen una gran influencia en las propiedades de los semiconductores y el rendimiento de los dispositivos. Las dislocaciones liberarán la tensión en los materiales [18]. También afectarán la corriente oscura y la capacidad de respuesta de los fotodetectores [19] e influirán en el IQE de múltiples pozos cuánticos [11, 20] y así sucesivamente. Sin embargo, pocas investigaciones se centran en la influencia de diferentes densidades de dislocación de subprocesos (TDD) en el índice de refracción de AlN, aunque existen TDD altas en los materiales de AlN, que generalmente varían de 10 ⁸ a 10 ⁹ cm ^{- 2} órdenes de informes recientes [21, 22, 23]. Investigar la correlación entre TDD y el índice de refracción de AlN es la clave para optimizar el rendimiento de los dispositivos optoelectrónicos. En este trabajo se ha estudiado la dependencia de diferentes TDD del índice de refracción de AlN. Se utilizan las diferentes longitudes de onda de los fotones, como 633 nm, 365 nm y 280 nm. Los resultados muestran que las dislocaciones conducen a la disminución del índice de refracción de AlN. Los resultados beneficiarán el diseño y la simulación de dispositivos optoelectrónicos basados en AlN, como los LED DUV y las estructuras DBR.

Métodos

Para estudiar la relación entre las dislocaciones y el índice de refracción de AlN, se cultivaron plantillas de AlN mediante deposición de vapor químico orgánico metálico (MOCVD) sobre sustratos de zafiro c y luego se recocieron a diferentes temperaturas para obtener muestras de AlN con diferentes densidades de dislocación.

Cuando se cultivaron moldes de AlN por MOCVD, se usaron trimetilaluminio y amoníaco como gases precursores. Se utilizó hidrógeno como gas portador. La presión durante el crecimiento se mantuvo a 40 mbar. La temperatura de crecimiento y el tiempo de la capa de nucleación es de aproximadamente 955 ° C durante 150 sy luego se eleva a 1280 ° C para el crecimiento de AlN a alta temperatura (HT). Después de 15 min de crecimiento de AlN a alta temperatura, se hizo crecer una capa intermedia de AlN a 1050 ° C durante 160 s. Finalmente, la temperatura de crecimiento se elevó a 1280 ° C para crecer HT AlN espeso durante 50 min. El espesor total de la película de AlN es de aproximadamente 1,1 μm.

Después del crecimiento de la capa de AlN por MOCVD, las plantillas de AlN se recocieron ex situ a 1500 ° C, 1600 ° C, 1700 ° C y 1750 ° C durante 1 h, respectivamente. La capa de AlN sin recocido se marcó como muestra 1, y las muestras después del recocido de 1500 ° C a 1750 ° C se marcaron como muestras 2 a 5. La difracción de rayos X (XRD) se utilizó para medir los TDD en muestras de AlN, y Se tomó la medida elipsométrica espectroscópica (SE) para medir el índice de refracción. Los espectros de cambio Raman se adoptaron para caracterizar el estado de tensión de las plantillas de AlN.

Resultados y discusión

Las Figuras 1 ayb muestran las curvas de oscilación XRD (XRD) del plano (0002) y (10-12) de las cinco muestras de AlN. Se puede observar que el ancho completo a la mitad del máximo (FWHM) del plano (0002) XRC disminuye levemente y el FWHM del plano (10-12) XRC disminuye en gran medida de la muestra 1 a la muestra 5. La densidad de dislocaciones con tornillo y borde El componente se puede calcular utilizando el FWHM de (0002) y (10-12) plano XRC de acuerdo con la fórmula (1) y (2):[24, 25].

$$ {\ rho} _ {\ mathrm {s}} ={\ beta _ {(0002)}} ^ 2 / \ left (2 \ pi \ ln 2 \ times {\ left | {b} _c \ right |} ^ 2 \ right) $$ (1) $$ {\ rho} _ {\ mathrm {e}} ={\ beta _ {\ left (10-12 \ right)}} ^ 2 / \ left (2 \ pi \ En 2 \ veces {\ left | {b} _a \ right |} ^ 2 \ right) $$ (2)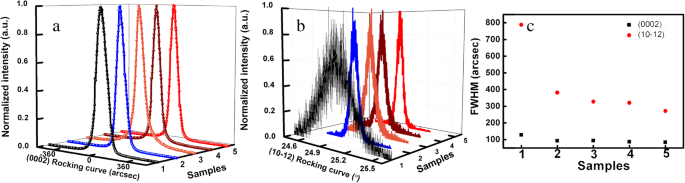

un El plano (0002) XRC de cinco muestras de AlN. b El plano (10-12) XRC de cinco muestras de AlN. c El FWHM del plano (0002, 10-12) XRC; el círculo rojo significa el FWHM del plano (10-12) y el cuadrado negro representa el FWHM del plano (0002)

donde ρ _s y ρ _e representan la densidad de la dislocación con el componente de tornillo y borde, respectivamente. β es el FWHM de XRC. | b _c | equivale a la constante de celosía c-axial, y | b _a | equivale a la constante reticular a-axial de AlN. El FWHM de (0002) y (10-12) plano XRC se muestran en la Fig. 1c para las cinco muestras de AlN y los TDD calculados de las cinco muestras de AlN se muestran en la Tabla 1.

Los datos experimentales SE de las cinco muestras se ajustan mediante el software CompleteEASE (J.A. Woollam Inc.) utilizando un modelo de semiconductor paramétrico, que puede reproducir las propiedades ópticas de los semiconductores de banda prohibida directa de forma eficaz [26]. La Figura 2a muestra las curvas experimentales y de ajuste parciales de las cinco muestras. El error cuadrático medio (MSE) de las cinco muestras es 8.139, 8.536, 9.175, 10.560 y 9.821, respectivamente, lo que confirma los buenos resultados de ajuste. Todos los datos y los resultados del ajuste se proporcionan en el archivo adicional 1.

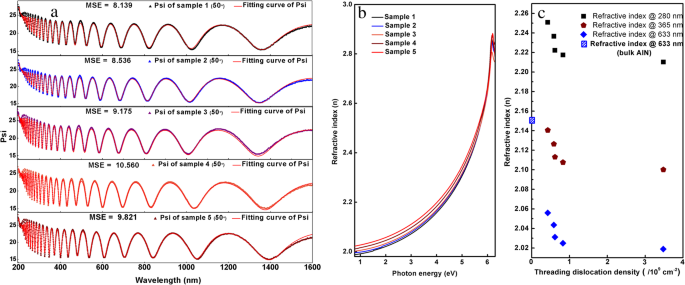
un Datos experimentales parciales de la medición SE y curvas de ajuste. b La curva del índice de refracción. c Índice de refracción frente a diferentes TDD a 280 nm, 365 nm y 633 nm

Las curvas del índice de refracción de las cinco muestras se pueden obtener a partir de los resultados del ajuste como se muestra en la Fig. 2b. Cuando la energía del fotón es menor que la banda prohibida de AlN (aproximadamente 6.2 eV), el índice de refracción aumenta al aumentar la energía del fotón para las cinco muestras. Sin embargo, cuando la energía de los fotones es superior a 6,2 eV, el índice de refracción disminuye con el aumento de la energía de los fotones. Este fenómeno puede describirse mediante la relación de dispersión de Kramers-Krőnig. Con la disminución de TDDs en AlN, el índice de refracción aumenta de 2.019 a 2.056 a 633 nm, que es más cercano al del AlN a granel (2.15 a 633 nm [27]). Significa que las dislocaciones en AlN hacen que el índice de refracción sea más pequeño que el del cristal de AlN a granel.

La relación entre el índice de refracción y los TDD a 4,42 eV (280 nm, UV ciego al sol), 3,40 eV (365 nm, banda prohibida de GaN) y 1,96 eV (633 nm) se muestran en la Figura 2c y en la Tabla 1. Se puede ver que el índice de refracción de AlN disminuye con el aumento de TDD. Con el aumento de las densidades de dislocación de 4,24 × 10 ⁸ a 3,48 × 10 ⁹ cm ^{- 2} , el índice de refracción de AlN disminuye de 2.2508 a 2.2102 a 280 nm.

Para revelar el mecanismo de cómo las dislocaciones cambian el índice de refracción de AlN, se estudia el campo de deformación inducido por las dislocaciones. La relación entre el índice de refracción y la deformación presentada se describe mediante la fórmula (3) [28]:

$$ \ Delta {\ left (\ frac {1} {n ^ 2} \ right)} _ i =PS =\ sum \ limits_ {ij} {p} _ {ij} {s} _j $$ (3)

En la fórmula, p _ij son el tensor elastoóptico y S es la presencia de tensión. La matriz de constantes fotoelásticas P de wurtzita AlN se muestra como la expresión (4) [29, 30].

$$ p =\ left (\ begin {array} {l} -0.1 \ kern1.75em -0.027 \ kern0.75em -0.019 \ kern1em 0 \ kern3em 0 \ kern2.75em 0 \\ {} -0.027 \ kern0.5em -0.1 \ kern2em -0.019 \ kern1em 0 \ kern3em 0 \ kern2.75em 0 \\ {} -0.019 \ kern0.5em -0.019 \ kern1em -0.107 \ kern1em 0 \ kern3em 0 \ kern2.75em 0 \\ {} 0 \ kern2.75em 0 \ kern3em 0 \ kern3.5em -0.032 \ kern0.75em 0 \ kern2.75em 0 \\ {} 0 \ kern2.75em 0 \ kern3em 0 \ kern3.5em 0 \ kern3em -0.032 \ kern0.5em 0 \\ {} 0 \ kern2.75em 0 \ kern3em 0 \ kern3.5em 0 \ kern3em 0 \ kern2.75em -0.037 \ end {array} \ right) $$ (4)

Se consideran las matrices del campo de deformación de la dislocación del tornillo y la dislocación del borde en AlN. Los modelos de anillo cilíndrico de los dos tipos de dislocación se describen en la Fig. 3. Según los modelos, se puede obtener la distribución del campo de deformación alrededor de una sola dislocación [31, 32].

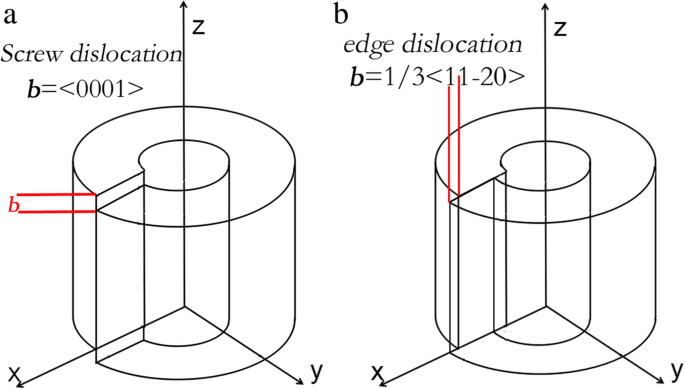
Modelo de anillo cilíndrico de a dislocación del tornillo y b dislocación del borde

El campo de deformación alrededor de la dislocación del tornillo de la unidad se puede escribir como:

$$ {e} _ {xz} ={e} _ {zx} =- \ frac {b} {4 \ pi} \ frac {y} {\ left ({x} ^ 2 + {y} ^ 2 \ derecha)} $$ (5) $$ {e} _ {yz} ={e} _ {zy} =\ frac {b} {4 \ pi} \ frac {x} {\ left ({x} ^ 2 + {y} ^ 2 \ right)} $$ (5a) $$ {e} _ {xx} ={e} _ {yy} ={e} _ {zz} ={e} _ {xy} ={ e} _ {yx} =0 $$ (5b)

El campo de deformación alrededor de la dislocación del borde de la unidad se puede escribir como:

$$ {e} _ {xx} =- \ frac {b} {4 \ pi \ left (1-v \ right)} \ frac {y \ left ({x} ^ 2- {y} ^ 2 \ right )} {{\ left ({x} ^ 2 + {y} ^ 2 \ right)} ^ 2} - \ frac {b} {2 \ pi} \ frac {y} {\ left ({x} ^ 2 + {y} ^ 2 \ right)} $$ (6) $$ {e} _ {yy} =\ frac {b} {4 \ pi \ left (1-v \ right)} \ frac {y \ left (3 {x} ^ 2 + {y} ^ 2 \ right)} {{\ left ({x} ^ 2 + {y} ^ 2 \ right)} ^ 2} - \ frac {b} {2 \ pi } \ frac {y} {\ left ({x} ^ 2 + {y} ^ 2 \ right)} $$ (6a) $$ {e} _ {zz} =\ frac {b \ left (\ lambda - 2 v \ lambda -2 Gv \ right)} {2 \ pi \ left (2G + \ lambda \ right) \ left (1-v \ right)} \ frac {y} {x ^ 2 + {y} ^ 2} $$ (6b) $$ {e} _ {xy} ={e} _ {yx} =\ frac {b} {4 \ pi \ left (1-v \ right)} \ frac {x \ left ({ x} ^ 2- {y} ^ 2 \ right)} {{\ left ({x} ^ 2 + {y} ^ 2 \ right)} ^ 2} $$ (6c) $$ {e} _ {xz } ={e} _ {zx} ={e} _ {yz} ={e} _ {zy} =0 $$ (6d)

donde b es la longitud del vector Burgers de dislocación unitaria y e representa la tensión alrededor de la dislocación. G =121 GPa es el módulo de corte de wurtzita AlN; λ =117,1 GPa y v =0.241 son la constante coja y la razón de Poisson [33, 34], respectivamente. Según la correspondencia entre e _ij y S _k ( yo , j = x , años , z ; k =1,2,3 ... 6) [35], convertimos el campo de deformación en una formación de matriz como se muestra a continuación para presentar aún más el cambio del índice de refracción causado por las dislocaciones.

$$ {S} _ {\ mathrm {edge}} =\ left ({S} _1 \ kern0.5em {S} _2 \ kern0.5em {S} _3 \ kern0.5em 0 \ kern0.5em 0 \ kern0. 5em {S} _6 \ right) $$ (7) $$ {S} _ {\ mathrm {tornillo}} =\ left (0 \ kern0.5em 0 \ kern0.5em 0 \ kern0.5em {S} _4 \ {S} _5 \ kern0.5em 0 \ right) $$ (8)

Tomando las matrices (7) y (8) en la fórmula (3), podemos obtener la expresión de Δ n causado por el tornillo de la unidad y la dislocación del borde de la unidad.

$$ \ Delta {\ left (\ frac {1} {n ^ 2} \ right)} _ {\ mathrm {tornillo}} ={\ left (\ frac {1} {n_1 ^ 2} - \ frac {1 } {n_0 ^ 2} \ right)} _ {\ mathrm {tornillo}} =- 0.032 \ left ({S} _4 + {S} _5 \ right) =- 0.008 \ frac {b \ left (xy \ right)} {\ pi \ left ({x} ^ 2 + {y} ^ 2 \ right)} $$ (9) $$ \ Delta {\ left (\ frac {1} {n ^ 2} \ right)} _ { \ mathrm {edge}} ={\ left (\ frac {1} {n_1 ^ 2} - \ frac {1} {n_0 ^ 2} \ right)} _ {\ mathrm {edge}} =- 0,146 \ left ( {S} _1 + {S} _2 \ right) -0.145 {S} _3-0.037 {S} _6 =\ hbox {-} 0.146 \ left (\ frac {b} {4 \ pi \ left (1-v \ right )} - \ frac {b} {2 \ pi} \ right) \ frac {2y} {x ^ 2 + {y} ^ 2} -0.145 \ frac {b \ left (\ lambda -2 \ lambda v-2 Gv \ right)} {2 \ pi \ left (2G + \ lambda \ right) \ left (1-v \ right)} \ frac {y} {x ^ 2 + {y} ^ 2} -0.037 \ frac {b } {4 \ pi \ left (1-v \ right)} \ frac {x \ left ({x} ^ 2- {y} ^ 2 \ right)} {{\ left ({x} ^ 2 + {y } ^ 2 \ right)} ^ 2} $$ (10)

Según el cálculo, las distribuciones del índice de refracción (tome el índice de refracción a 633 nm como ejemplo) alrededor de las dislocaciones del tornillo de la unidad y del borde de la unidad se muestran en la Fig. 4. Muestra que el índice de refracción alrededor de la dislocación cambia a lo largo de la dirección radial del núcleo de dislocación que puede considerarse un medio no homogéneo. Por tanto, la luz que se propaga en AlN se verá influida en consecuencia por los TDD. La dispersión y la interferencia ocurrirán [36] cuando la luz atraviese estos campos refractivos alrededor de las dislocaciones. Como resultado, se cambiará el índice de refracción de AlN, que corresponde a la matriz de dispersión del medio no homogéneo [37].

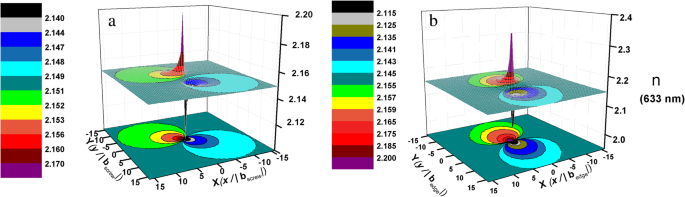
La distribución del índice de refracción a 633 nm alrededor de a dislocación del tornillo de la unidad y b dislocación del borde de la unidad

Como se mencionó en la sección “Introducción”, se deben evitar otros factores de influencia para demostrar que el índice de refracción está realmente influenciado por las dislocaciones. Todas las muestras se midieron a temperatura ambiente para evitar la influencia de la temperatura. Para obviar la influencia de la tensión en el material de AlN, se tomó el espectro Raman para confirmar la tensión en AlN y los resultados se muestran en la Fig. 5. La E _g modo pico de zafiro a 750 cm ^{- 1} se toma como calibración. El pico de cambio Raman de AlN E ₂ ( h ) el azul cambia con la disminución de TDD como se muestra en la Tabla 1. El cambio azul de E ₂ ( h ) pico significa que el AlN sufre cada vez más tensión de compresión debido al sustrato de zafiro. Sin embargo, con el aumento de la tensión de compresión, el índice de refracción se acerca al del AlN a granel a 633 nm. Se puede obtener claramente que la tensión de AlN que sufre de sustratos heterogéneos tiene poca influencia sobre el índice de refracción. Evidencia adicional para apoyar la conclusión es que el índice de refracción de AlN también es menor que el de AlN a granel cuando AlN sufre tensión de tracción del sustrato de Si [38], que es lo mismo que la condición de que AlN sufra tensión de compresión en este trabajo. Este fenómeno se puede atribuir al hecho de que la tensión que sufre el AlN por los sustratos es demasiado pequeña para realizar un cambio significativo en el índice de refracción del AlN. Como resultado, en comparación con la influencia de otros factores, el efecto de la tensión de los sustratos sobre el índice de refracción de AlN puede despreciarse.

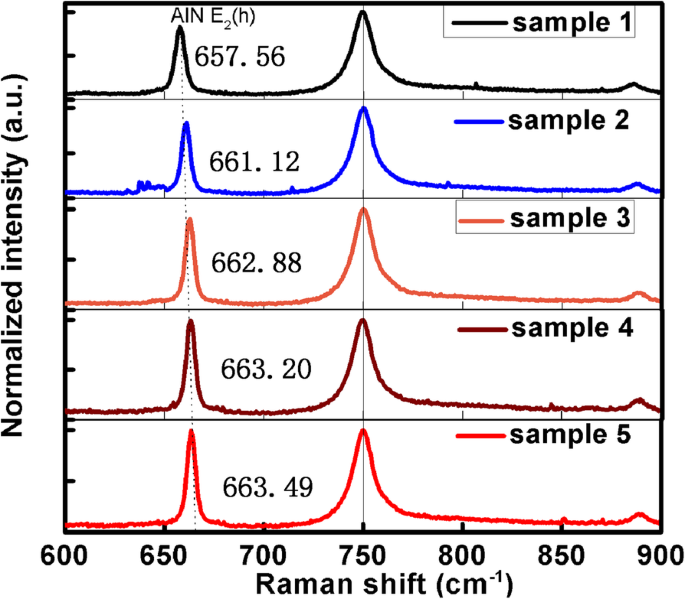
Espectros de cambio Raman de las cinco muestras

Aquí también se calcula la banda prohibida de las cinco muestras. El coeficiente de absorción óptica α se extrae de los resultados del ajuste SE, y luego la banda prohibida E _g se calcula según la fórmula siguiente [39]:

$$ {\ left (\ alpha E \ right)} ^ 2 =\ left \ {\ begin {array} {c} C \ left (E- {E} _g \ right) \ kern0.75em \ left (E \ ge {E} _g \ right) \\ {} 0 \ kern4.75em \ left (E <{E} _g \ right) \ end {array} \ right. $$ (11)

La trama de ( αE ) ² frente a E se presenta como la Fig. 6. La intersección de la x -axis es el valor de E _g . Desde la intersección de las curvas de ajuste en la x -eje, el aumento de la banda prohibida de 6.1106 a 6.1536 eV para la muestra 1 a la muestra 5 se muestra en la Fig. 6. La relación entre el índice de refracción y la banda prohibida se muestra a continuación [16].

$$ n (E) ={\ left [a {\ left (\ frac {E} {E_g} \ right)} ^ 2 \ left (2 - {\ left (1+ \ frac {E} {E_g} \ derecha)} ^ {0.5} - {\ izquierda (1- \ frac {E} {E_g} \ derecha)} ^ {0.5} \ derecha) + b \ derecha]} ^ {0.5} $$ (12)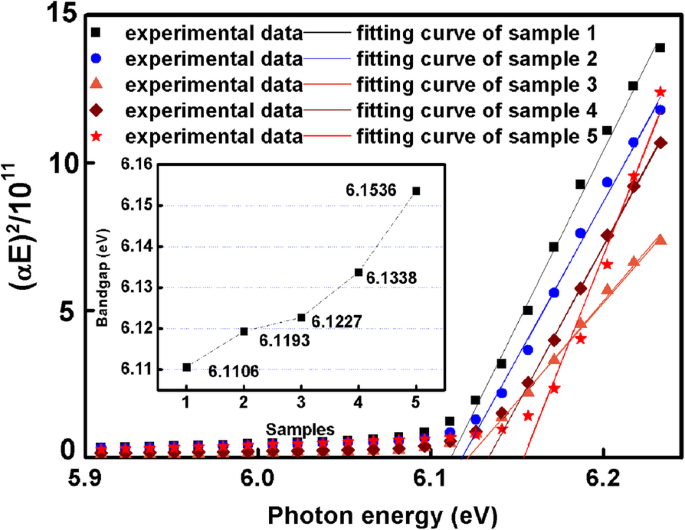

Dependencia de ( αE ) ² en ( E ), la imagen insertada muestra la banda prohibida de las plantillas de AlN

donde E es la energía del fotón y E _g es la banda prohibida de AlN. a y b son constantes que equivalen a 13,70 y 7,81 para AlN, respectivamente. El índice de refracción de AlN debería disminuir con el aumento de E _g según la fórmula. Sin embargo, en este trabajo, el índice de refracción de AlN aumenta con el aumento de E _g , lo que significa que la influencia de la banda prohibida en el índice de refracción de AlN puede despreciarse en comparación con la influencia de los TDD. Por lo tanto, el cambio de TDD juega un papel clave en el cambio del índice de refracción de AlN.

Combinado con los análisis anteriores, se confirma que el campo de deformación a nanoescala influirá en la distribución del índice de refracción alrededor de las dislocaciones, lo que influirá aún más en el índice de refracción de AlN. Las dislocaciones disminuirán la refracción de AlN según los datos experimentales.

Conclusiones

En conclusión, el efecto de los TDD sobre el índice de refracción de AlN se estudia tanto de forma experimental como teórica. Obviando la influencia de la temperatura, el estrés y la banda prohibida, se puede llegar a la conclusión de que el índice de refracción de AlN disminuye con el aumento de los TDD. Otros estudios demostraron que el campo de deformación a nanoescala alrededor de las dislocaciones da como resultado que el índice de refracción cambie significativamente alrededor de las dislocaciones. La dispersión y la interferencia ocurrirán una vez que la luz se propague a través de dislocaciones y, por lo tanto, se cambiará el índice de refracción de AlN. Los resultados de este trabajo serán beneficiosos para optimizar los dispositivos optoelectrónicos DUV basados en AlN.

Disponibilidad de datos y materiales

Todos los datos se pueden proporcionar en una solicitud adecuada.

Abreviaturas

DBR:: Reflector Bragg distribuido
DUV:: Ultravioleta profundo
EQE:: Eficiencia cuántica externa
FWHM:: Ancho completo a la mitad del máximo
LED:: Diodos emisores de luz
LEE:: Eficiencia de extracto ligero
MOCVD:: Deposición de vapor químico metalorgánico
MSE:: Error cuadrático medio
SE:: Elipsométrico espectroscópico
TDD:: Densidades de dislocación de subprocesos
XRC:: Curva oscilante XRD
XRD:: Difracción de rayos X

Transiciones de fase y formación de una estructura tipo monocapa en películas delgadas de oligotiofeno:exploración con una difracción de rayos X in situ y mediciones eléctricas combinadas Sensor de presión flexible capacitivo basado en papel de alto rendimiento y su aplicación en mediciones relacionadas con humanos

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias