Transmisión de diodo óptico dicroico en dos rejillas metálicas paralelas dislocadas
Resumen
Se propone e investiga numéricamente una estructura de diodo óptico con dos rejillas metálicas paralelas dislocadas. La transmisión de diodo óptico dicroico se realiza en esta estructura, es decir, el efecto de diodo óptico se observa en dos bandas de ondas correspondientes a direcciones de transmisión inversas. En la estructura, dos rejillas metálicas paralelas con diferentes constantes de rejilla están separadas por una losa dieléctrica en el medio. La primera rejilla iluminada actúa como un selector para excitar plasmones de superficie a una longitud de onda adecuada. La otra rejilla actúa como un emisor para realizar la transmisión óptica. Cuando se invierte la dirección del incidente, las funciones de dos rejillas se intercambian y los plasmones de superficie se excitan en otra longitud de onda. En las bandas de onda de transmisión dicroica, la estructura del diodo óptico exhibe una transmisión extraordinaria y posee un alto aislamiento óptico de hasta 1. Además, las bandas de onda operativas se pueden modular cambiando los parámetros de la estructura.
Introducción
El diodo óptico, que transmite fotones en una dirección y prohíbe la transmisión en la dirección inversa, ha atraído una atención considerable en virtud de la propiedad de transmisión unidireccional [1]. Los fenómenos de diodos ópticos se pueden observar cuando se rompe la simetría de inversión de tiempo de la interacción luz-materia. Se puede aplicar campo magnético externo [2], voltaje de polarización [3], onda acústica [4] o modulación dependiente del tiempo [5, 6] para lograr el efecto de diodo óptico. Además, la estructura de ruptura de simetría de inversión espacial es una opción alternativa, como estructuras asimétricas multicapa [7], cristales fotónicos asimétricos [8] y rejillas asimétricas [9]. En las últimas décadas, las micro-nanoestructuras metálicas han ganado un gran interés debido a las propiedades prometedoras de los plasmones de superficie (SP). Los dispositivos plasmónicos se proponen en muchos campos de investigación, como la holografía de metasuperficie [10, 11, 12, 13, 14], el sensor de índice de refracción [15, 16] y el filtro [17, 18]. Los dispositivos plasmónicos pueden modificar fuertemente la interacción de los campos electromagnéticos en nanoescala [19]. La modulación de los SP se puede realizar cambiando el entorno dieléctrico circundante y los parámetros geométricos de las estructuras metálicas [20, 21]. Diodos ópticos compuestos de estructuras metálicas a nanoescala, por ejemplo, rejillas intercaladas de capa plasmónica [22, 23], rejillas plasmónicas en cascada [24, 25], nanoagujeros plasmónicos [26], guía de ondas de ranura plasmónica [27] y agregados de nanopartículas plasmónicas [28] , se investigan ampliamente con el propósito de procesar información óptica.
En este trabajo, la transmisión de diodos ópticos dicroicos se obtiene en dos rejillas metálicas paralelas dislocadas intercalando una placa dieléctrica. Tanto la mejora de la transmisión como la alta relación de contraste de aislamiento se logran en las dos bandas de onda operativas con direcciones de transmisión inversas, porque las rejillas metálicas que constan de rendijas estrechas exhiben una transmisión de luz extraordinaria [29, 30] y las estructuras asimétricas realizan una transmisión unidireccional [27,28,29,30 , 31]. Según el orden de iluminación, dos rejillas metálicas con diferentes constantes de rejilla actúan como selector y emisor respectivamente. El selector selecciona la longitud de onda de resonancia excitando los SP y, con la contribución de los SP, el emisor realiza la transmisión de luz. Cuando se invierte la dirección del incidente, los roles de dos rejillas se intercambian y los SP se excitan en otra longitud de onda. Por tanto, se obtiene la transmisión de diodo óptico dicroico. El grosor de la estructura del diodo óptico propuesto en este artículo es tan pequeño como 160 nm. Con el desarrollo de las tecnologías de nanofabricación, se pueden aplicar muchos métodos a la fabricación de estructuras de rejillas metálicas, como la litografía por nanoimpresión ultravioleta [32], la litografía de escritura directa con láser [33] y la litografía por haz de electrones [34]. El carácter del diodo óptico es independiente de la intensidad incidente. Estas propiedades implican que nuestra estructura tiene amplios potenciales en integración óptica.
Métodos
El esquema de la estructura del diodo óptico se muestra en la Fig. 1. La estructura consta de dos rejillas de plata G 1 y G 2 intercalando una capa de sílice. El espesor de la capa de sílice se indica como d . G 1 y G 2 tienen el mismo ancho de hendidura s , del mismo grosor h y diferentes constantes de rejilla Λ i ( yo =1, 2). La estructura es simétrica traslacional y la celda unitaria contiene 2 unidades de G 1 y 3 unidades de G 2 . Δ denota la posición relativa lateral de G 1 y G 2 en una celda unitaria. El modelo Drude [35] se utiliza para describir la función dieléctrica de la plata. El índice de refracción de la sílice es de 1,5, ignorando su dispersión. El dieléctrico circundante es aire y su índice de refracción es 1. Onda plana incidente normal de p -La polarización se emplea para investigar el efecto del diodo óptico.
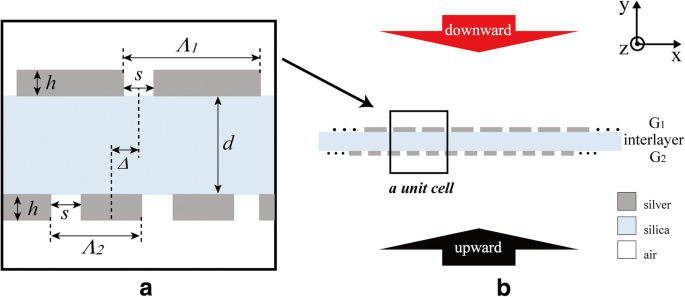
Diagrama esquemático de la estructura del diodo óptico. un La celda unitaria. b Vista general
Transmitancia T de la estructura del diodo óptico se define de la siguiente manera:
$$ T =\ frac {p_o} {p_i}, $$ (1)donde P i es la potencia incidente y P o es la potencia de salida. T se simula numéricamente mediante el método de diferencia finita en el dominio del tiempo (FDTD) [36]. Se emplean condiciones de contorno periódicas en los lados izquierdo y derecho, y se aplican límites de capa de coincidencia perfecta en los lados superior e inferior de nuestro modelo de simulación. T D y T U representan la transmitancia para la incidencia descendente y la incidencia ascendente, respectivamente. La propiedad del diodo óptico se describe mediante la relación de contraste de aislamiento η :
$$ \ eta =\ frac {\ left | {T} _D \ hbox {-} {T} _U \ right |} {T_D + {T} _U}. $$ (2)Por lo tanto, η =1 significa el mejor rendimiento de diodo óptico.
Resultados y análisis teóricos
La transmitancia y la relación de contraste de aislamiento de la estructura del diodo óptico se muestran en la Fig. 2. T D es diferente a T U cuando la longitud de onda incidente es menor que λ C . T D alcanza el valor máximo 0,73 y T U es 3,7 × 10 −3 en λ D (1315 nm). Considerando que T U alcanza el valor máximo 0.82 y T D es 3.6 × 10 −4 en λ U (921 nm). Las relaciones de contraste de aislamiento en λ D y λ U son 0.990 y 0.999, respectivamente. La Figura 2 muestra que el efecto de diodo óptico se obtiene alrededor de λ D y λ U , y las dos bandas de ondas tienen direcciones de transmisión inversas. En las bandas de onda de funcionamiento del diodo dicroico, la estructura exhibe una transmisión extraordinaria.
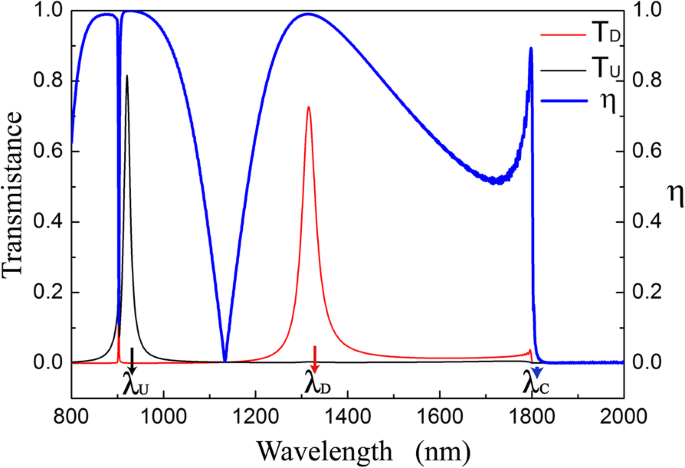
Espectros de transmisión y relación de contraste de aislamiento de la estructura del diodo óptico con d =200 nm, s = h =50 millas náuticas, Λ 1 =900 nm, Λ 2 =600 nm y Δ =0 nm
Para comprender la transmisión del diodo óptico dicroico, la intensidad del campo eléctrico | E | 2 en dos bandas de onda operativas se simulan. Como se muestra en la Fig. 3a, d, el campo eléctrico se mejora entre dos rejillas cuando la luz se transmite a través de la estructura del diodo óptico. Mientras tanto, las Fig. 3b, c muestran el estado de bloqueo inverso. La mejora del campo electromagnético entre dos rejillas se debe a los SP en dos interfaces de plata / sílice adyacentes. Los tipos de SP en dos redes son diferentes, que se clasifican como SP estructurados (SSP) y SP inducidos (ISP) respectivamente. SSP se excita y genera en la primera rejilla iluminada (selector). Los ISP se inducen en la última rejilla (emisor) por el acoplamiento entre los SPP y la interfaz adyacente plata / sílice. Debido a los SSP y los ISP, la luz se transmite a través de la estructura del diodo óptico.
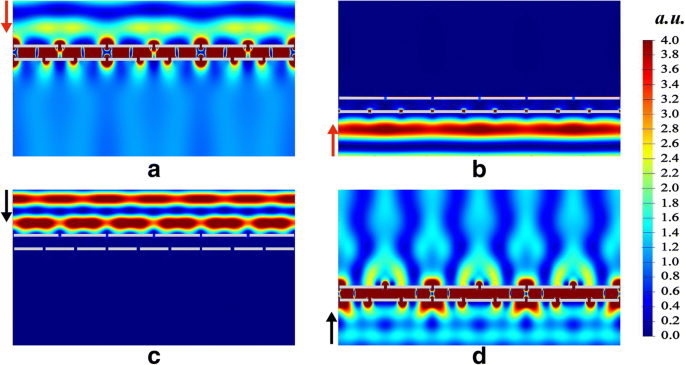
Distribuciones de la intensidad del campo eléctrico | E | 2 para incidencia a la baja en λ D =1315 nm ( a ), incidencia al alza en λ D =1315 nm ( b ), incidencia a la baja en λ U =921 nm ( c ) e incidencia ascendente en λ U =921 nm ( d )
Densidad de carga superficial en la interfaz plata / sílice y E y Los componentes de la distribución del campo eléctrico se ilustran en la Fig. 4 para revelar las funciones de acoplamiento de los SP. En la figura 4a, G 1 y G 2 tienen cargas opuestas en sus superficies adyacentes, que es similar al condensador de placa plana. Bajo la condición de incidencia a la baja, G 1 actúa como un selector para excitar a los SSP en λ D . La distribución periódica de la densidad de carga superficial representa que los SPP se determinan mediante la constante de rejilla de G 1 . G 2 apoya a los ISP inducidos por los SPP y actúa como emisor para la transmisión. E y entre G 1 y G 2 se mejora debido al acoplamiento entre los SPP y los ISP, como se muestra en la Fig. 4b. Para la condición de incidente ascendente que se muestra en la Fig. 4c, d, G 2 actúa como selector y G 1 actúa como emisor.
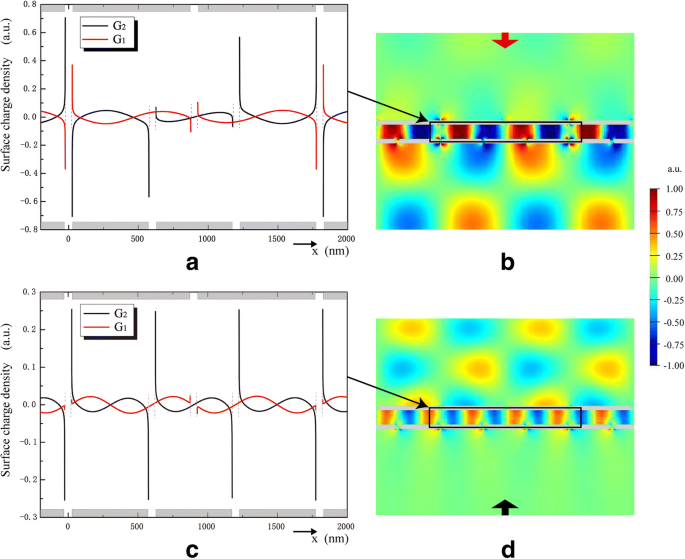
La densidad de carga superficial en la interfaz plata / sílice en G 1 y G 2 , bajo la condición de incidencia a la baja en λ D =1315 nm ( a ) e incidencia ascendente en λ U =921 nm ( c ). Ey componente del campo eléctrico bajo la condición de incidencia descendente en λ D =1315 nm ( b ) e incidencia ascendente en λ U =921 nm ( d )
Como puede verse en la Fig.4, el campo de transmisión es periódico y no uniforme en la horizontal ( x -eje) dirección. El período Λ ( Λ =2 Λ 1 =3 Λ 2 ) de la distribución de campo de transmisión está modulada por la estructura de diodo óptico integral y satisface 2π / Λ =| g 1 -g 2 |, aquí g i es el vector de rejilla de G i ( yo =1, 2). La eficiencia de difracción de la red aumenta por la existencia de SP. El vector de onda lateral κ de luz transmitida se deriva de la superposición de g 1 y g 2 :
$$ \ kappa =\ pm \ frac {2 \ pi} {\ Lambda} =\ pm \ left | {g} _1- {g} _2 \ right |, $$ (3)Y decide la longitud de onda crítica λ C ( λ C =2π / | κ |) para T D ≠ T U . Según Eq. (3), λ C es 1800 nm para nuestra estructura mencionada anteriormente, lo que está de acuerdo con los resultados de la simulación λ C =1806 nm mostrado en la Fig. 2. Los efectos del diodo óptico aparecen en el rango de λ ≤ λ C . Según los resultados de la simulación, el período de las rejillas integradas (1800 nm) es mayor que las longitudes de onda de funcionamiento del diodo (1315 nm y 921 nm). Se pueden obtener componentes de difracción de múltiples órdenes con la dispersión de luz de las rejillas integradas. Por lo tanto, el campo de transmisión no es uniforme a lo largo de la dirección paralela a las rejillas, incluso cuando la luz se transmite al campo lejano.
Los SSP de la rejilla de plata son similares a los SP en la interfaz planar plata / sílice, excepto que los SSP son de modo radiativo [37], mientras que los SP son modos completamente ligados a la superficie. Los SSP pueden tratarse como SP en la interfaz plana de plata / sílice aproximadamente cuando las ranuras de las rejillas son extremadamente estrechas. Entonces, la relación de dispersión de los SSP se puede escribir de la siguiente manera [38]:
$$ \ beta ={k} _0 \ sqrt {\ frac {\ varepsilon_m {\ varepsilon} _d} {\ varepsilon_m + {\ varepsilon} _d}} $$ (4)donde k 0 es el vector de onda espacial libre y ɛ m y ɛ d son el coeficiente dieléctrico de la plata y la sílice, respectivamente. La relación de dispersión descrita por la Ec. (4) se ilustra en la Fig. 5. La curva de dispersión calculada usando los parámetros del modelo Drude [35] en este documento encaja bien con la calculada usando los conjuntos de datos de constante óptica de Johnson y Christy [39] cuando la energía del fotón es inferior a 2.75 eV ( λ > 450 nm). En la Fig.5, las líneas de trazos verticales rojas y negras representan | g 1 | y | g 2 |, respectivamente. Los SSP se excitan con la rejilla cuando se cumple la condición de coincidencia de vectores [40]:
$$ \ beta ={k} _0 \ sin \ theta \ pm {Ng} _i \ left (N =1,2,3 \ dots \ right). $$ (5)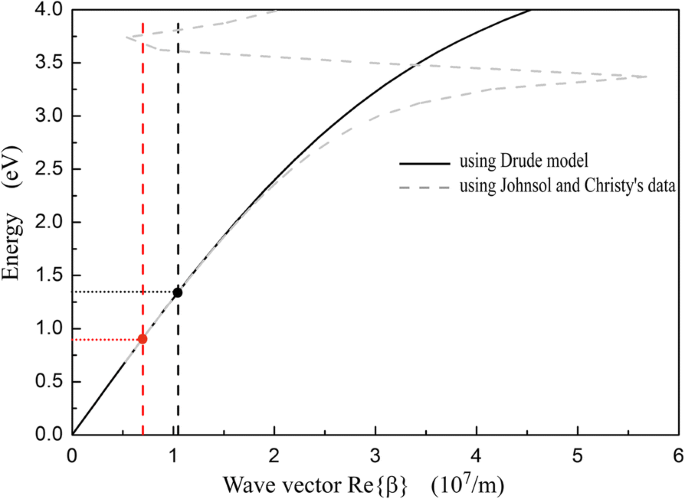
Dispersión de SP en la interfaz plana de plata / sílice calculada mediante el modelo de Drude y los datos de la constante óptica de Johnson y Christy. Las líneas de trazos verticales rojas y negras representan el módulo del vector de rejilla | g 1 | y | g 2 |, respectivamente
Para incidencia normal ( θ =0 °), el de primer orden ( N =1) la difracción de una rejilla tiene la mayor eficiencia de difracción, es decir, la mayor eficiencia de excitación para los SSP. Por tanto, la ecuación. (5) se cumple en los puntos rojo y negro que se muestran en la Fig.5:
$$ \ beta =\ mid {g} _i \ mid. $$ (6)En la estructura del diodo óptico, G 1 es el selector para excitar a los SSP para la incidencia a la baja y G 2 es el selector de incidencia al alza. G 1 y G 2 tienen diferentes constantes de rejilla, por lo que los SSP se excitan en diferentes longitudes de onda para direcciones de incidentes inversas. En la figura 5, la energía del fotón en el punto rojo es 0,91 eV y la longitud de onda es 1365 nm, que corresponde a λ D (1315 nm) que se muestra en la Fig. 2. De manera similar, la energía del fotón indicada por el punto negro es 1.04 eV y su longitud de onda es 924 nm, correspondiente a λ U (921 nm) en la Fig. 2. Como la aproximación de la rejilla a la placa, las longitudes de onda de resonancia de SSP calculadas mediante la ecuación. (4) y Eq. (6) no son exactamente iguales a los simulados mediante el uso de métodos FDTD que se muestran en la Fig. 2.
La ecuación (5) indica que el ángulo de incidencia θ influye en la condición de coincidencia del vector de onda de la rejilla con los SSP. Con el cambio de θ , la relación de contraste de transmisión y aislamiento en λ D (1315 nm) y λ U (921 nm) se simulan y se muestran en la Fig. 6a, b, respectivamente. Con θ aumentando de 0 ° a 10 °, T D en λ D y T U en λ U disminución de la discordancia del vector de onda entre g i y SSP. ( T D en λ D disminuye a 0 cuando θ ≈ 40 ° y T U en λ U disminuye a 0 cuando θ ≈ 35 °.) En un rango de ángulo de incidencia de 0 ° ≤ θ ≤ 5 °, T D en λ U y T U en λ D son casi 0 y η siempre se mantiene mayor que 0.98 en ambos λ U y λ D . La Figura 6 demuestra que la estructura muestra un buen efecto de diodo óptico en λ D y λ U bajo incidencia de ángulo pequeño.
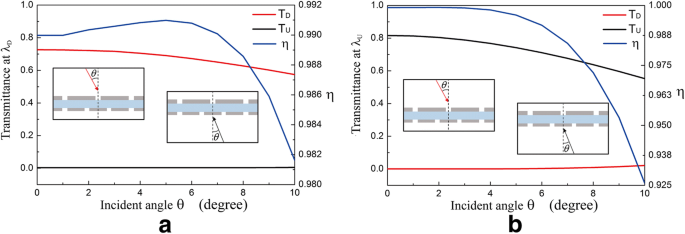
La influencia del ángulo incidente en la transmitancia y la relación de contraste de aislamiento en λ D =1315 nm ( a ) y λ U =921 nm ( b )
Investigación y discusión
En esta sección, investigamos la influencia de los parámetros de la estructura en los espectros de transmisión y la relación de contraste de aislamiento.
El espesor de la capa intermedia d y rejillas posición relativa lateral Δ están limitados por la precisión de fabricación. La influencia de d y Δ sobre los espectros de transmisión y las relaciones de contraste de aislamiento se muestran en las Figs. 7 y 8, respectivamente. La Figura 7 muestra que las bandas de onda operativas del diodo óptico exhiben un ligero desplazamiento al rojo cuando d aumenta. Mientras tanto, el valor máximo de T D disminuye muy poco, pero el valor máximo de T U disminuye significativamente. El aumento de d alargará la distancia de transmisión de luz a través de la estructura, debilitará la interacción electromagnética entre G 1 y G 2 y perjudican la densidad de carga inducida en la superficie del emisor. Como se ve en la Fig. 4, las cargas distribuidas en las esquinas de las ranuras del emisor actúan como fuentes de dipolos eléctricos del campo de transmisión. Densidad de carga en las esquinas de las ranuras del emisor G 2 (Fig. 4a) es mucho mayor que en las esquinas de las ranuras del emisor G 1 (Fig. 4c), entonces d influye menos en el valor máximo de T D que el de T U . Además, con el aumento de d , picos pequeños marcados como FP 1 y FP 2 aparecer en T U y el pico de transmisión de FP 1 exhibe un gran corrimiento al rojo. Intensidad de campo eléctrico | E | 2 distribuciones prueban que FP 1 y FP 2 resultado de resonancias de Fabry-Perot.
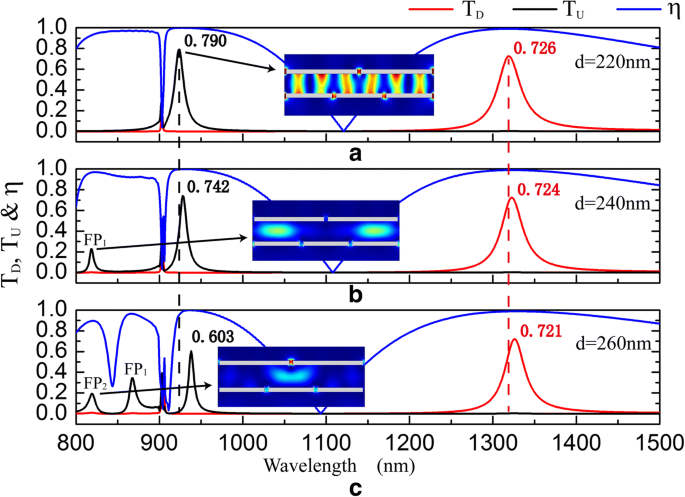
La influencia de d sobre los espectros de transmisión y la relación de contraste de aislamiento. d =220 nm ( a ), d =240 nm ( b ) y d =260 nm ( c ) cuando s = h =50 millas náuticas, Λ 1 =900 nm, Λ 2 =600 nm y Δ =0 nm. Los recuadros son distribuciones de la intensidad del campo eléctrico | E | 2 para resonancias de transmisión ascendente
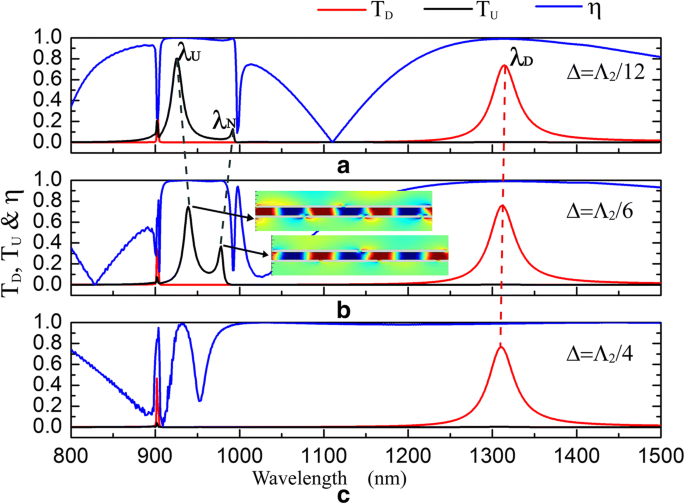
La influencia de Δ sobre los espectros de transmisión y la relación de contraste de aislamiento. Δ =50 nm = Λ 2 / 12 ( a ), Δ =100 nm = Λ 2 / 6 ( b ) y Δ =150 nm = Λ 2 / 4 ( c ) cuando d =200 nm, s = h =50 millas náuticas, Λ 1 =900 nm y Λ 2 =600 nm. Las inserciones en ( b ) son E y distribuciones para resonancias de transmisión ascendente
Como se muestra en la Fig.1, la estructura del diodo óptico es periódica y tiene la misma celda unitaria cuando Δ =a ± M Λ 2 / 2 (0 nm < a < Λ 2 / 2 y M =0, 1, 2…). Además, la celda unitaria de Δ = a es simétrico de giro de izquierda a derecha con el de Δ = - a ± M Λ 2 / 2 y pueden realizar el mismo efecto de transmisión. Entonces, la transmitancia de la estructura del diodo óptico se ve afectada por Δ como: T ( Δ ) = T ( Δ + Λ 2 / 2) =T (- Δ + Λ 2 / 2). Como se muestra en la Fig.8, efecto de diodo óptico en λ ~ 921 nm se enciende y apaga en un período de Λ 2 / 2 como Δ aumenta. Sin embargo, el pico de transmisión de T D exhibe un ligero desplazamiento hacia el azul y el efecto de diodo óptico en λ ~ 1315 nm está siempre encendido cuando Δ aumenta. Visto en la Fig. 8a, un nuevo pico de transmisión en λ N emerge en T U curva cerca de λ U . Cuando Δ aumenta de Λ 2 / 12 a Λ 2 / 6, el pico en λ N muestra un desplazamiento hacia el azul mientras que el pico en λ U exhibe un corrimiento al rojo (Fig. 8a, b). E y distribuciones para resonancias de transmisión en λ U y λ N se insertan en la Fig. 8b. Según los resultados de la simulación, la resonancia en λ N genera debido a la división de energía. Cuando Δ aumenta a Λ 2 / 4, que se muestra en la Fig. 8c, T U se suprime y dos resonancias de transmisión desaparecen, lo que hace que el efecto de diodo óptico se apague en λ ~ 921 nm.
Según el análisis de la teoría, la banda de ondas operativa del diodo óptico se puede obtener en un cierto rango optimizando los parámetros de la red. La Figura 9 muestra que la transmisión del diodo óptico dicroico se logra en el rango de luz visible con parámetros de estructura d =100 nm, Λ 1 =450 nm, Λ 2 =300 nm, s = h =30 nm y Δ =0 nm. Las transmitancias máximas de las bandas de ondas de transmisión de diodos dicroicos son 80% (a 522 nm para incidencia ascendente) y 71% (a 732 nm para incidencia descendente), y las correspondientes relaciones de contraste de aislamiento η son 0,998 y 0,993.
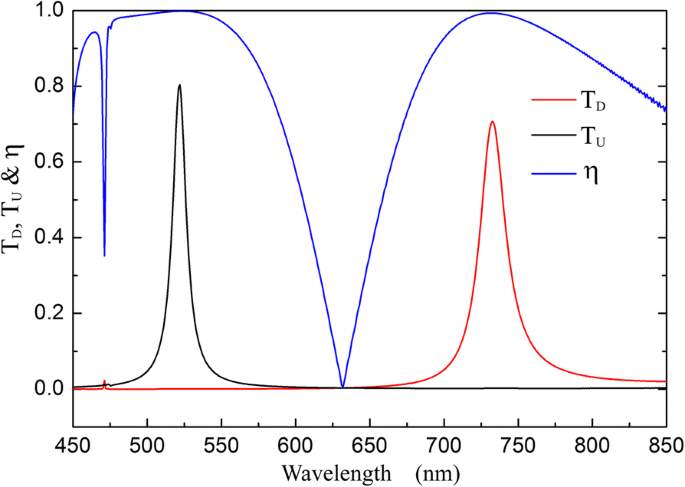
Espectros de transmisión y relación de contraste de aislamiento para la estructura del diodo óptico con d =100 nm, Λ 1 =450 nm, Λ 2 =300 nm, s = h =30 nm y Δ =0 nm
Además, el componente de la celda unitaria en nuestra estructura también influye en los fenómenos del diodo óptico. Según Eq. (5), las bandas de ondas del efecto de diodo dependen de Λ 1 y Λ 2 . En nuestra investigación, seleccionamos la celda unitaria que consta de 2 unidades de G 1 y 3 unidades de G 2 , es decir, 2 Λ 1 =3 Λ 2 , para obtener altas transmitancias y buenas relaciones de contraste de aislamiento en las bandas de onda del diodo óptico simultáneamente. Por ejemplo, la Fig. 10 muestra la transmisión dicroica de la estructura del diodo óptico con su celda unitaria que consta de 3 unidades de G 1 y 4 unidades de G 2 . Los efectos del diodo óptico se obtienen a 530 nm con T U =72% y 659 nm con T U =76%. Las relaciones de contraste de aislamiento en las dos longitudes de onda se reducen a 0,912 y 0,987, porque la diferencia de | g 1 | y | g 2 | es pequeño y la rejilla que actúa como selector puede excitar los SSP de ambas rejillas con diferentes eficiencias. Además, cuando Λ 1 =2 Λ 2 , la resonancia de transmisión de SP en la estructura del diodo óptico causada por la difracción de primer orden de G 2 también puede excitarse por la difracción de segundo orden de G 1 por 2 g 1 = g 2 , lo que reduciría la relación de contraste de aislamiento. Entonces, la buena propiedad del diodo óptico requiere que dos constantes de rejilla tengan una diferencia suficiente y eviten la relación de múltiplos enteros.
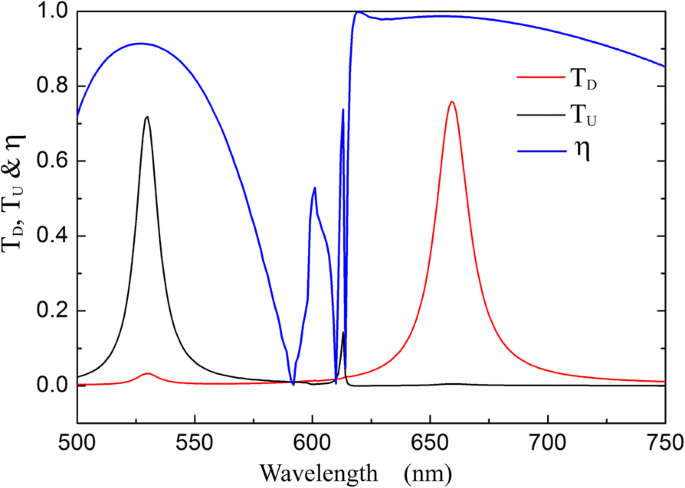
Espectros de transmisión y relación de contraste de aislamiento para la estructura del diodo óptico con la celda unitaria que incluye 3 unidades de G 1 y 4 unidades de G 2 . d =100 nm, Λ 1 =400 nm, Λ 2 =300 nm, s = h =30 nm y Δ =0 nm
Conclusiones
La transmisión de diodo óptico dicroico basada en SP se realiza en nuestra estructura, que consta de dos rejillas de plata paralelas dislocadas y una capa intermedia de sílice. La primera rejilla metálica iluminada selecciona la banda de ondas de transmisión excitando SSP, y la otra rejilla metálica emite energía electromagnética hacia adelante a través de las oscilaciones de electrones superficiales. Cuando se invierte la dirección de incidencia de la luz, los roles de dos rejillas se intercambian y aparece otra banda de ondas de transmisión de diodos ópticos. La relación de aislamiento óptico puede alcanzar casi hasta 1. Las bandas de ondas de transmisión de diodos ópticos se pueden ajustar para que estén en diferentes regiones cambiando los parámetros de la estructura. Las bandas de onda de funcionamiento del diodo óptico y la transmitancia son independientes de la intensidad incidente. El grosor de la estructura es de solo unos pocos cientos de nanómetros. Estas propiedades de nuestra estructura proporcionan una amplia gama de aplicaciones en circuitos integrados.
Abreviaturas
- ISP:
-
Plasmones superficiales inducidos.
- SP:
-
Plasmones de superficie
- SSP:
-
Plasmones de superficie estructurada
Nanomateriales



