Método para medir parámetros de movimiento de varios grados de libertad basado en rejillas de difracción de polidimetilsiloxano de acoplamiento cruzado

Resumen

Este trabajo presenta un método de medición de parámetros de movimiento de múltiples grados de libertad basado en el uso de rejillas de difracción de acoplamiento cruzado que se prepararon en los dos lados de un sustrato de polidimetilsiloxano (PDMS) utilizando tecnología de procesamiento de plasma de oxígeno. El rayo láser que viaja a través de la rejilla óptica de acoplamiento cruzado se difractaría en una matriz de puntos bidimensionales. El desplazamiento y el tamaño de la brecha de la matriz de puntos eran funciones del movimiento de la fuente láser, como se explica por el efecto de difracción de Fraunhofer. Se utilizó un dispositivo de carga acoplada (CCD) de 480 × 640 píxeles para adquirir imágenes de la matriz de puntos bidimensionales en tiempo real. Luego se utilizó un algoritmo propuesto para obtener los parámetros de movimiento. Utilizando este método y el CCD descrito anteriormente, las resoluciones del desplazamiento y el ángulo de deflexión fueron de 0,18 μm y 0,0075 rad, respectivamente. Además, un CCD con un mayor número de píxeles podría mejorar las resoluciones del desplazamiento y el ángulo de deflexión a escalas subnanométricas y micro radianes, respectivamente. Por último, las posiciones dinámicas de los helicópteros flotantes se han rastreado y comprobado mediante el método propuesto, que se puede utilizar para corregir la posición de la nave y proporcionar un método para la estabilización de la aeronave en el cielo.

Antecedentes

Los parámetros de movimiento de varios grados de libertad pueden proporcionar información precisa de ubicación y actitud sobre un objetivo específico, que se ha utilizado ampliamente para estructuras grandes en aplicaciones como el control de la estabilidad de actitud de la aeronave, la estabilidad de puntería de los sistemas de sonda de armas, el brazo robótico movimiento, alineación de piezas de precisión y posicionamiento de piezas de trabajo para procesamiento industrial [1,2,3].

Por lo tanto, se utilizaron métodos de detección de alta precisión para detectar información de varios grados de libertad (p. Ej., Rectitud, inclinación y ángulo de deflexión) sobre los objetivos, y estos métodos requerían sensores de alto rendimiento, incluida la característica de detección de alta velocidad. , sincronización, alta precisión de medición y en tiempo real. Estos métodos se utilizaron ampliamente en aplicaciones aeroespaciales, vehículos aéreos no tripulados, fabricación de precisión y alineación óptica [4, 5, 6].

El método de medición precisa en tiempo real y el desacoplamiento de la información dinámica de movimiento de múltiples grados de libertad fueron los elementos clave para determinar la estabilidad de actitud del portaaviones. Hsieh [7] propuso una matriz de detección tridimensional que usaba tres grupos de módulos para detectar los diferentes grados de libertad, en la que se usaban diferentes módulos de detección para medir la información de posición diferente y se usaba un algoritmo para calcular los ángulos y múltiples información sobre grados de libertad. Liu [8] presentó un método de medición de parámetros de movimiento de múltiples grados de libertad basado en el cambio en el ángulo relativo entre dos rejillas de ensamblaje para realizar las mediciones de información. Sin embargo, el enfoque anterior era propenso a ser los errores de ensamblar dos o más elementos sensores y la complejidad de los cálculos de acoplamiento, y su precisión también depende del sistema de instrumentos de alta precisión.

Con el desarrollo de la tecnología de fabricación de micro-nano, nanotecnología y nanomateriales, los investigadores han estudiado los métodos de detección de parámetros de movimiento de múltiples grados de libertad basados en la implementación de un solo chip, desde la perspectiva de la miniaturización y la aplicación de bajo costo en el campos de nanomateriales, materiales ópticos y nanodispositivos. Tana [9] informó de un algoritmo de detección de parámetros de movimiento de varios grados de libertad con un haz sin difracción basado en una estructura de prisma miniaturizado portátil, que podría minimizar los errores de medición. Nuestro equipo ha presentado un método de medición de deformación vectorial basado en un solo elemento sensor que se puede aplicar a las mediciones de deformación vectorial de superficie utilizando sensores mecánicos integrados de múltiples ejes y proporcionó la base para la investigación en este artículo [8, 10].

En este trabajo, se ha demostrado un método de medición de ángulos y desplazamiento vectorial de múltiples grados de libertad basado en un solo elemento; este elemento se fabricó utilizando tecnología de procesamiento de plasma de oxígeno para formar una estructura de rejilla óptica de gradiente ortogonal en ambos lados de un sustrato de polidimetilsiloxano (PDMS) que se dobló previamente en forma de elipse. Estas rejillas ópticas cruzadas pueden hacer que un rayo láser de entrada se difracte en una matriz de puntos bidimensionales. La información de ubicación del punto de difracción se puede utilizar para lograr el ángulo del haz incidente calculado por el algoritmo de ubicación en tiempo real. Según este método y un dispositivo de carga acoplada (CCD) de 480 × 640 píxeles, las resoluciones de medición del desplazamiento y el ángulo de deflexión fueron de 0,18 μm y 0,0075 rad, respectivamente. Además, el CCD de píxeles más altos puede mejorar la resolución de medición del desplazamiento y el ángulo de deflexión a niveles subnanométricos y microradianes, respectivamente. Finalmente, se ha seguido la posición dinámica de un helicóptero en vuelo estacionario utilizando el método propuesto en tiempo real; la información adquirida se puede utilizar para corregir la posición de la nave y demuestra un nuevo método para la estabilización de aeronaves en el cielo.

Experimental

Preparación de polidimetilsiloxano (PDMS)

El PDMS (Sylgard 184) se adquirió de Dow Corning. Se prepararon membranas de PDMS (10:1) mediante revestimiento por centrifugación sobre obleas de silicio y se curaron inmediatamente después de centrifugar a temperaturas inferiores a 80ºC durante 2 h. Se prepararon sustratos de PDMS con un espesor de 600 μm controlando la velocidad de hilado.

Preparación de rejilla ortogonal doble

De acuerdo con los requisitos experimentales, las películas PDMS se prepararon con un área de 3 × 3 cm ² . A continuación, las películas de PDMS se filtraron previamente en relación con el original 1,5 veces en la dirección X utilizando una etapa de traducción casera. SiO arrugado _x Luego se formaron capas en el O ₂ Sustrato de PDMS pretensado tratado con plasma (IoN Wave 10, PVA-TePla, Alemania) en condiciones de un caudal de oxígeno de 30 sccm y un tiempo de oxidación de 40 s. Se formaron estructuras de nanorejilla uniformes y ordenadas en la superficie del sustrato de PDMS después de relajar el pretensado. Como se muestra en la Fig. 1a, este proceso se repitió tomado en el otro lado del sustrato PDMS con una diferencia angular de 90 °, para formar las estructuras de rejilla ortogonales en ambos lados del sustrato PDMS.

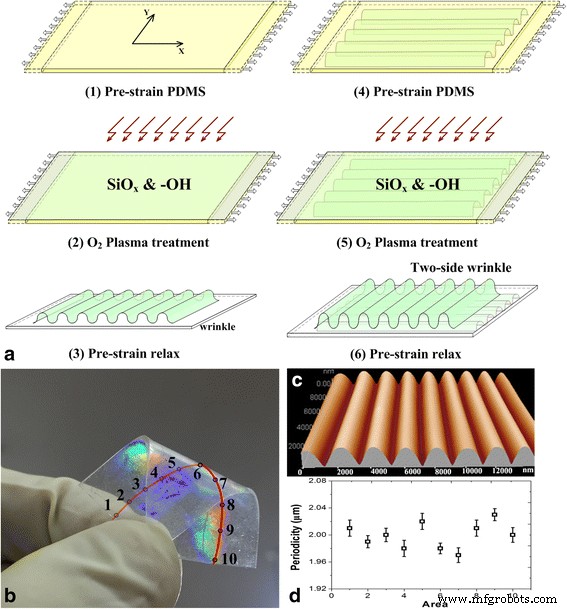
Proceso de fabricación y caracterizaciones morfológicas de la rejilla óptica doble PDMS. un Fabricación de doble rejilla óptica. b Las imágenes ópticas de la rejilla. c Imagen de microscopía de fuerza atómica de la rejilla. d La uniformidad de periodicidad de las muestras

Construcción de plataforma de prueba

El sistema de sensor de ángulo de desplazamiento de cuatro grados de libertad que se ha construido incluye una fuente de luz láser, un conjunto de plataforma de desplazamiento y ángulo, un portamuestras, una pantalla, una cámara CCD y una computadora. Como se muestra en la Fig.2, se instaló una fuente de luz láser He-Ne (longitud de onda láser de 680 nm) en el ensamblaje de la plataforma de ángulo y desplazamiento que consistía en una plataforma giratoria eléctrica y un marco de ajuste tridimensional manual (Beijing Zolix Instrument Co., Ltd .). La plataforma tiene una precisión de rotación de 0,1 ° y una precisión de desplazamiento de 2 μm. Esta rejilla óptica cruzada puede hacer que el rayo láser se difracte en una matriz de puntos bidimensionales. Se utilizó una cámara complementaria de óxido de metal-semiconductor (CMOS) con 480 × 640 píxeles para adquirir una imagen de la matriz de puntos bidimensionales en tiempo real utilizando algoritmos de procesamiento de imágenes MATLAB, que se utilizó para extraer la ubicación de cada punto de difracción y luego calcular el x- y y -desplazamientos de eje y la información de ángulo. Se proporcionó una plataforma de prueba en forma de un avión de cuatro rotores (Typhoon Q500, Yuneec Electric Aviation). Y se adquirió información de cuatro grados de libertad para obtener la actitud de vuelo estacionario en interiores.

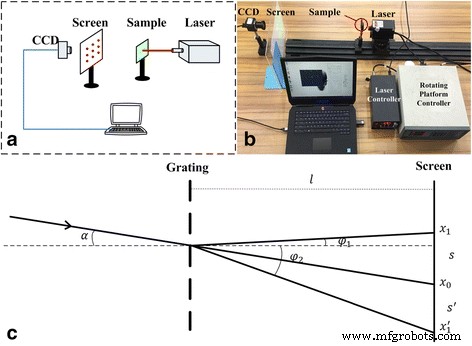
El principio y sistema de prueba para el parámetro de movimiento MODF. un sistema de diagrama. b Configuración del sistema. c Principio de prueba de desplazamiento y ángulo

Análisis y discusión

Caracterización de rejilla PDMS ortogonal

El proceso de fabricación se muestra como en la Fig. 1a. La modificación de la superficie hidrófila de PDMS utilizó la tecnología de plasma de oxígeno. Un SiO _x La capa y los grupos hidrófilos (p. ej., -OH) se formaron así sobre los sustratos de PDMS precurvados por el plasma de oxígeno. Cuando la tensión previa en el sustrato de PDMS supera un valor crítico, se formaron estructuras de rejilla en la superficie de PDMS después de la relajación previa a la tensión [11, 12]. La periodicidad de las rejillas se logró mediante el ajuste de las condiciones de predoblado y plasma aplicadas y se puede calcular en nuestros trabajos anteriores. Como se muestra en la Fig. 1c, las topografías de las micro / nano redes se caracterizaron por microscopía de fuerza atómica (AFM) (CSPM5500; Benyuan Co.). Como se muestra en la Fig. 1b, d, se han seleccionado 10 áreas a lo largo de la línea central en un lado de la muestra para estudiar la periodicidad y uniformidad de las estructuras de rejilla. La periodicidad correspondiente de las rejillas de 10 áreas fue uniforme y tuvo un período de (2 ± 0.05) μm en toda la superficie de la muestra.

Rejilla de difracción para caracterización de parámetros de movimiento de ángulo y posición

El rayo láser viaja a través de la muestra (con la rejilla) para difractar en la matriz de puntos de luz, de acuerdo con la teoría de difracción de Fraunhofer [13]. La posición del punto de difracción estaba directamente relacionada con la posición y el ángulo del haz incidente y, por lo tanto, la información de posición del haz incidente puede detectarse mediante la información de ubicación de los puntos de difracción.

La Figura 2 muestra la plataforma móvil y giratoria para rastrear el posicionamiento y los puntos de difracción correspondientes del haz incidente. Según la teoría de difracción de Fraunhofer, cuando la red de difracción y la distancia de la pantalla son fijas, la relación entre el haz incidente, el haz difractado y la longitud de onda se puede expresar de la siguiente manera:

$$ d \ left (\ sin \ varphi \ pm \ sin \ alpha \ right) =m \ lambda \ left (m =0,1,2, \ dots \ right) $$ (1)

Aquí, λ era la longitud de onda del haz incidente, d fue el período de la rejilla, α era el ángulo de incidencia, φ era el ángulo de difracción, y m era el orden de difracción de rejilla.

Cuando el ángulo de incidencia α no era igual a 0, "+" indica que el haz de difracción y el haz incidente se distribuyen en el mismo lado de la normal de rejilla, mientras que "-" indica que el haz de difracción y el haz incidente existen en dos lados de la normal. En un ángulo de incidencia específico, las distancias entre el primer orden de puntos de difracción y el orden cero de puntos de difracción no eran iguales en la pantalla. Por tanto, la distancia entre los puntos puede cambiar con el ángulo de incidencia. El ángulo del haz incidente se puede calcular cuantitativamente mediante el cálculo de la posición del punto de luz de difracción. Simultáneamente, la ubicación móvil del haz incidente provoca un movimiento del punto de difracción de orden cero. La información de la posición del haz incidente se puede calcular mediante la información de ubicación del punto del haz de difracción de orden cero.

La Figura 2c muestra una sola dirección del diagrama de difracción de rejilla, donde x ₀ fue el primer orden de puntos de difracción, y x ₁ y \ ({x} _1 ^ {\ hbox {'}} \) indican el segundo orden de puntos de difracción. De la Fig. 2c, s y s ’Eran la distancia entre el primer y segundo orden de puntos de difracción que se expresaron de la siguiente manera:

$$ s =l \ tan \ alpha + l \ tan {\ varphi} _1 $$ (2) $$ {s} ^ {\ hbox {'}} =l \ tan \ alpha -l \ tan {\ varphi} _2 $$ (3)

De la Eq. (1):

$$ d \ left (\ sin {\ varphi} _1 + \ sin \ alpha \ right) =\ lambda $$ (4) $$ d \ left (\ sin {\ varphi} _2- \ sin \ alpha \ right) =\ lambda $$ (5)

A partir de lo anterior, el modelo de correlación entre el ángulo de incidencia del haz y el espaciado de moteado de difracción se puede obtener como:

$$ s =l \ tan \ alpha + \ tan \ left (\ arcsin \ left (\ frac {\ lambda} {d} - \ sin \ alpha \ right) \ right) $$ (6) $$ {s} ^ {\ hbox {'}} =l \ tan \ alpha - \ tan \ left (\ arcsin \ left (\ frac {\ lambda} {d} + \ sin \ alpha \ right) \ right) $$ (7)

Detección y caracterización de parámetros de movimiento de múltiples grados de libertad basados en rejillas de difracción ortogonal

El rayo láser que viaja a través de una rejilla óptica unidireccional puede formar puntos de difracción únicos. La orientación ortogonal se puede formar a medida que el rayo láser viaja pasando las rejillas ortogonales en los dos lados del sustrato PDMS. Se formará un haz de difracción de rejilla unidimensional cuando se transmita un haz de luz a lo largo de la dirección de la rejilla en un lado de la pantalla y las dimensiones se establecieron en x -eje. Luego se formó un haz de difracción de rejilla unidimensional ortogonal a la x -eje cuando un haz de luz pasa a lo largo de la dirección de la rejilla en el otro lado de la pantalla y la dimensión se estableció en el y -eje. Se formó una matriz de puntos de difracción bidimensional en la pantalla, como se muestra en la Fig. 3b.

El parámetro de movimiento MODF depende del movimiento de los puntos de difracción. un Se generaron puntos de difracción unidimensionales mediante la rejilla unidireccional. b La matriz de puntos bidimensionales se generó mediante la rejilla óptica de doble cruz. c El movimiento de la matriz de puntos se controló mediante el movimiento de la fuente láser. d El espacio que se mueve entre la matriz de puntos se controló como el ángulo de incidencia del rayo láser

Cuando se cambió la posición de un rayo láser, el orden cero de la posición del punto de luz de difracción mostrará un movimiento correspondiente, y la posición del mapa de bits de difracción cambiará en consecuencia según la teoría de difracción de Fraunhofer. La posición del haz incidente se puede calcular directamente en función de la dirección del movimiento de la celosía, y luego se detecta la información de la posición de realización del haz de luz a lo largo de x- y y -eje. Como se muestra en la Fig. 3c, el primer orden de la posición del punto de difracción no puede calcular con precisión el desplazamiento de la luz debido a los efectos de acoplamiento del desplazamiento y la desviación. Además, el orden cero de la ubicación del punto de difracción solo estaba relacionado con la ubicación de la fuente. Por lo tanto, sería más preciso utilizar el orden cero del desplazamiento del punto de difracción para calcular la posición de la fuente de luz. Como se muestra en la Fig. 3d, la información del ángulo de deflexión de los rayos de luz incidente a lo largo de la x -eje y el y -eje se puede calcular por la distancia entre el punto de luz en el x -eje y el y -eje basado en el modelo relacionado entre el ángulo y el cambio del punto.

Sin embargo, la limitación del motivo del desplazamiento de los puntos de difracción depende del ángulo de incidencia y la distancia entre la rejilla y la pantalla según la Eq. (1). En nuestros trabajos, la rejilla se fijó con la pantalla, lo que significa que la variación de distancia entre la rejilla y la pantalla era cero. No hubo desplazamiento de puntos de difracción cuando la fuente láser se movía a lo largo de la z -eje. Además, cuando la fuente láser giraba a lo largo de la z eje, la variación del ángulo de incidencia fue cero, lo que resultaría en un no desplazamiento de los puntos de difracción.

En nuestros experimentos, el cambio de ángulo (Δ θ _x ) a lo largo de la x -eje se puede calcular en términos de los espacios entre columnas ( s _x , \ ({s} _x ^ {\ hbox {'}} \)) de los puntos de difracción, y el cambio de ángulo (∆ θ _y ) a lo largo de la y -eje se puede calcular en función de los espacios entre columnas ( s _y , \ ({s} _y ^ {\ prime} \)) de los puntos de difracción. La plataforma de la cartera se ajustó para cambiar la ubicación de la fuente de luz, y luego el software MATLAB adquirió las imágenes de la cámara cada 0.02 s para extraer la posición de los puntos de difracción para compararlos con valores anteriores, que se utilizó para calcular los desplazamientos de la matriz de puntos en el x -eje y el y -eje y los cambios en el espaciado de columnas y el espaciado de filas de la matriz.

Según el algoritmo, el desplazamiento de la matriz de puntos se puede analizar manipulando la imagen antes y después del movimiento para calcular ∆ x , ∆ años , ∆ θ _x y ∆ θ _y . Debido a que el punto láser incluye varios píxeles en la imagen y su energía estaba de acuerdo con la distribución gaussiana, se utilizó el método de ajuste de distribución gaussiana para eliminar el ruido de fondo de la imagen para extraer la ubicación del centro del punto láser con precisión. La función gaussiana del punto láser se expresa de la siguiente manera:

$$ I \ left (x, y \ right) =H \ cdot \ exp \ left \ {- \ left [\ frac {{\ left (x \ hbox {-} xo \ right)} ^ 2} {\ sigma_1 ^ 2} + \ frac {{\ left (y \ hbox {-} yo \ right)} ^ 2} {\ sigma_2 ^ 2} \ right] \ right \} $$ (8)

Aquí, yo ( x , años ) fue la intensidad del punto y H era la amplitud, ( x ₀ , años ₀ ) eran las coordenadas del centro del punto de luz, y σ ₁ , σ ₂ fueron las desviaciones estándar de la x -eje y el y -eje, respectivamente.

Se puede aplicar un logaritmo a ambos lados de la ecuación anterior para obtener la ubicación del centro del punto, que se puede expresar de la siguiente manera:

$$ {x} _0 =- \ frac {c} {2a} $$ (9) $$ {y} _0 =- \ frac {d} {2b} $$ (10)

Aquí, a , b , c y d fueron los coeficientes polinomiales que se obtuvieron mediante el ajuste gaussiano de todos los píxeles en el lugar.

Los cambios de distancia entre dos puntos de difracción se han calculado mediante dos imágenes antes y después del movimiento. Y el punto central de los puntos de difracción se ha establecido como el sistema de centros de coordenadas antes del movimiento:el desplazamiento absoluto y los sistemas de coordenadas de desplazamiento relativo del punto de luz. El sistema de coordenadas de desplazamiento absoluto del punto de luz de difracción tomó como referencia una pantalla de quietud. La información de movimiento ( Δx , Δy ) de la red en ambas pantallas se puede calcular por el orden cero de la coordenada del punto de difracción (es decir, la posición central). El sistema de coordenadas de desplazamiento relativo para el punto de luz tomó como referencia el orden cero del punto de difracción, que se puede usar para calcular los cambios en el espaciado de la matriz de puntos ( S _x ) y el espacio entre filas ( S _y ).

La Figura 4 mostró la caracterización de los cuatro grados de libertad. Cuando el rayo láser cortaba a lo largo de la x -eje, hubo un movimiento correspondiente de la red de difracción en el x -eje, pero el desplazamiento fue de aproximadamente cero en el y -eje. La sensibilidad del desplazamiento fue de aproximadamente 5,4 píxeles / μm. Este método se puede utilizar para calcular la información de ubicación de la fuente de luz a lo largo del eje con alta precisión, como se muestra en la Fig. 4a.

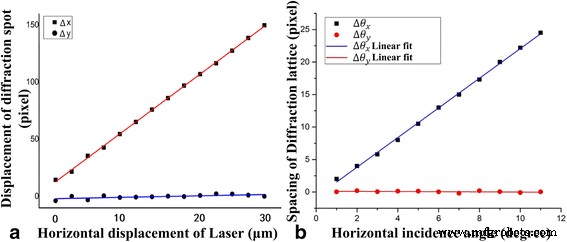
Caracterización de cuatro grados de libertad. un El desplazamiento de la fuente láser depende del desplazamiento de los puntos de difracción. b El ángulo de incidencia de la fuente láser depende del espacio entre los puntos de difracción

Cuando el láser giró un pequeño ángulo a lo largo de la x -eje, hubo un cambio de distancia correspondiente del espaciado de fila de la matriz de puntos de difracción y el espaciado de columna de la matriz de puntos fue cero. La sensibilidad del desplazamiento fue de aproximadamente 2,3 píxeles por ángulo (/ °). Mientras tanto, el rango de medición del ángulo fue de aproximadamente 9,8 ° en teoría calculado por las Ecs. (1) - (5) como la distancia s =0. Atribuir al primer orden de puntos de difracción coincide con el orden cero de puntos de difracción, ya que al aumentar el ángulo de incidencia, el cambio de distancia de los puntos de difracción sería cero ( s =0). Este método se puede utilizar para obtener la información del ángulo de la fuente de luz a lo largo de x -eje. La información de ubicación y ángulo también se puede obtener usando este método.

La resolución de detección de un píxel depende del algoritmo basado en el software MATLAB. Como se calculó anteriormente, el método tiene una sensibilidad de desplazamiento de 5,4 píxeles / μm, lo que significa que la resolución fue de 0,18 μm . Para la sensibilidad de desplazamiento de 2,3 píxeles / ° , fue una resolución de 0.0075 rad. Esto muestra que, según el método presentado aquí y la resolución del CCD, las resoluciones del desplazamiento y el ángulo fueron de 0,18 μm y 0,0075 rad, respectivamente. El CCD de 480 × 640 píxeles se utilizó para adquirir la imagen de la matriz de puntos bidimensionales en tiempo real. Además, el CCD de píxeles más altos y la optimización de la trayectoria de la luz podrían mejorar las resoluciones del desplazamiento y el ángulo de deflexión hasta escalas subnanométricas y micro radianes, respectivamente.

Caracterización de información de parámetros de movimiento de rotor de aeronave flotante

Un giroavión era un tipo de sistema de aeronave civil no tripulada con baja precisión, que se usaba ampliamente en los campos aéreo, de modelos de aeronaves y de navegación. El control de estabilidad de un helicóptero representa un microcosmos de una plataforma de combate no tripulada. Para realizar un control de vuelo de alta precisión, el aspecto más importante era el control constante de la actitud y la posición de la aeronave. Y el aspecto central fue la decodificación de la información de posición y actitud de vuelo estacionario de alta precisión en tiempo real, de modo que la información precisa de los parámetros de movimiento de cuatro grados de libertad sobre el vuelo estacionario se convierte en un activo esencial.

En nuestro experimento, basado en una rejilla de difracción de acoplamiento cruzado, se ha presentado un método de medición para lograr la información de actitud de cuatro grados de libertad del vuelo de la aeronave en tiempo real. Primero, se usó un avión de cuatro rotores para reemplazar la plataforma, que estaba compuesta por la posición y la postura de un sistema de prueba de cuatro grados de libertad, que se basaba en una rejilla doble para configurar los cuatro grados de libertad. -sistema de prueba de actitud de libertad para aviones de cuatro rotores. En el sistema de prueba, se fijó un pequeño puntero láser en el centro de una aeronave de cuatro rotores como fuente de luz y proyecta los rayos láser verticalmente hacia abajo. Una muestra con la rejilla doble, una pantalla y una cámara giran a lo largo del centro del eje óptico. Esta rejilla óptica cruzada puede hacer que el rayo láser se difracte en una matriz de puntos bidimensionales. En los experimentos, la cámara se utilizó para adquirir la imagen de la pantalla y transmitir imágenes a la computadora en tiempo real para calcular la información de desplazamiento mediante el software MATLAB.

Para lograr mediciones rápidas, precisas y en tiempo real de las señales de vuelo, un avión de cuatro rotores estaba flotando en el aire y rastreaba rápidamente la señal de postura mantenida durante 4 s. Información sobre los desplazamientos axiales a lo largo de la x -eje y el y -eje para aviones de cuatro rotores se han obtenido en un tiempo de 4 s, como se muestra en la Fig. 5c. Sobre la base del establecimiento de un sistema de coordenadas planas (es decir, una x -eje y una y -eje), la x y y los valores se convierten en estos puntos de coordenadas. Los resultados de posicionamiento 200 en 4 s significan un punto adquirido en 0,02 s. Esto representa el uso del método de seguimiento de la aeronave cada 0.02 s en tiempo real para determinar su ubicación y posición. La aeronave tiene un desplazamiento máximo de 2,1 mm en el x -eje y desplazamiento máximo de 2,3 mm en la y -eje, según el algoritmo.

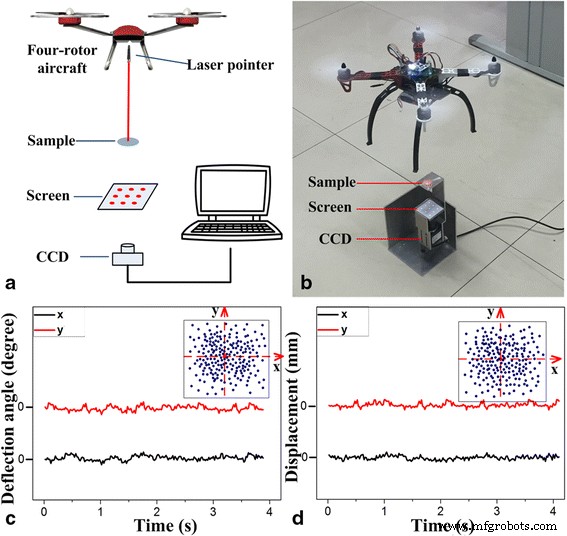
Caracterizaciones de la actitud de las embarcaciones de cuatro rotores. un Sistema de diagrama. b Configuración del sistema. c Ángulo de deflexión de la nave del rotor. d Desplazamiento de la nave de rotor

Además, la información del ángulo de cabeceo y del ángulo de alabeo de la aeronave se ha calculado mediante el algoritmo y el método de procesamiento de datos anteriores. Como se muestra en el recuadro de la Fig. 5d, el diagrama de puntos del ángulo de rotación de la aeronave de cuatro rotores proporcionó información precisa sobre el ángulo de la aeronave mediante el seguimiento en tiempo real cada 0,02 s. Observó que la aeronave tiene una desviación angular máxima de 1 ° en el x -eje y el y- eje. Por lo tanto, este método puede calcular la información de cuatro grados de libertad para la aeronave, que puede retroalimentar las señales precisas de posición y ángulo al sistema de control de vuelo dentro de 0.02 s para mejorar la estabilidad de la aeronave.

Conclusiones

En resumen, se demostró una tecnología simple fabricable para fabricar la estructura de rejilla óptica ortogonal con una periodicidad de 2 μm en los dos lados del sustrato PDMS. Basado en la estructura de rejilla óptica ortogonal, se ha estudiado un método para identificar la posición del haz y una información de parámetro de movimiento angular utilizando la información de posición del punto de luz de difracción basada en el efecto de difracción de Fraunhofer. Se utilizó un CCD de 480 × 640 píxeles para adquirir imágenes de la matriz de puntos bidimensionales en tiempo real. Los resultados muestran que, al utilizar este método y el CCD descrito anteriormente, las resoluciones del desplazamiento y el ángulo de deflexión fueron de 0,18 μm y 0,0075 rad, respectivamente. Además, con el CCD de píxeles más alto, las resoluciones del desplazamiento y el ángulo de deflexión pueden mejorar hasta escalas subnanométricas y micro radianes, respectivamente. Este método se puede utilizar para detectar posiciones precisas de vuelo estacionario e información de ángulo para aeronaves de rotor en tiempo real con alta precisión cada 0.02 s. La información se puede devolver para controlar el sistema de vuelo de los vehículos aéreos no tripulados en el aire. Este método era simple, de bajo costo y de alta precisión y puede realizar un monitoreo en tiempo real al tiempo que proporciona una base de investigación para un vuelo estable y un control preciso de aeronaves para plataformas de combate no tripuladas.

Síntesis y propiedades electroquímicas de materiales de cátodo LiNi0.5Mn1.5O4 con dopaje compuesto Cr3 + y F− para baterías de iones de litio Estudio de los primeros principios sobre la estabilidad y la imagen STM del borofeno

Nanomateriales