Resonancias Fano de banda dual de factor de alta calidad inducidas por estados de doble enlace en el continuo utilizando una losa de nanoagujeros plana

Métodos

Estructura y diseño de celosía

La Figura 1 muestra la geometría esquemática del PNS propuesto y sus espectros de transmisión. El PNS consta de cuatro nanoagujeros que pueden encogerse (Δ <0) o expandirse (Δ> 0) con una distancia de desplazamiento de Δ a lo largo de las diagonales de la superrejilla, y Δ =0 corresponde a una red simple con un período reducido a la mitad, donde cada nanoagujero está ubicado en el centro de un cuarto de área de la superrejilla. El período y la altura del PNS son Λ y H, respectivamente; el radio del nanoagujero es r . El índice de refracción del SNP es n _s =3.2, y el fondo es aire con un índice de refracción de n _a =1. La Figura 1c muestra los espectros del SNP en función de la distancia de desplazamiento de Δ, donde el SNP está iluminado por una x que incide normalmente -luz polarizada. Los espectros, así como las distribuciones de campo electromagnético de los PNS presentados en este artículo, se calculan utilizando el software comercial del método de elementos finitos de COMSOL Multiphysics. Como se muestra en la Fig. 1c, no hay resonancia de Fano para el SNP no encogido con Δ =0. Sin embargo, se pueden obtener dos resonancias de Fano con profundidades de modulación del 100% (definidas como las diferencias de transmisión entre los picos de Fano y las caídas de Fano) mediante encogiendo o expandiendo ligeramente los nanoagujeros. En comparación con la respuesta de transmisión del SNP no encogido, la respuesta de transmisión del SNP encogido varía abruptamente mientras que las bandas laterales se mantienen casi iguales.

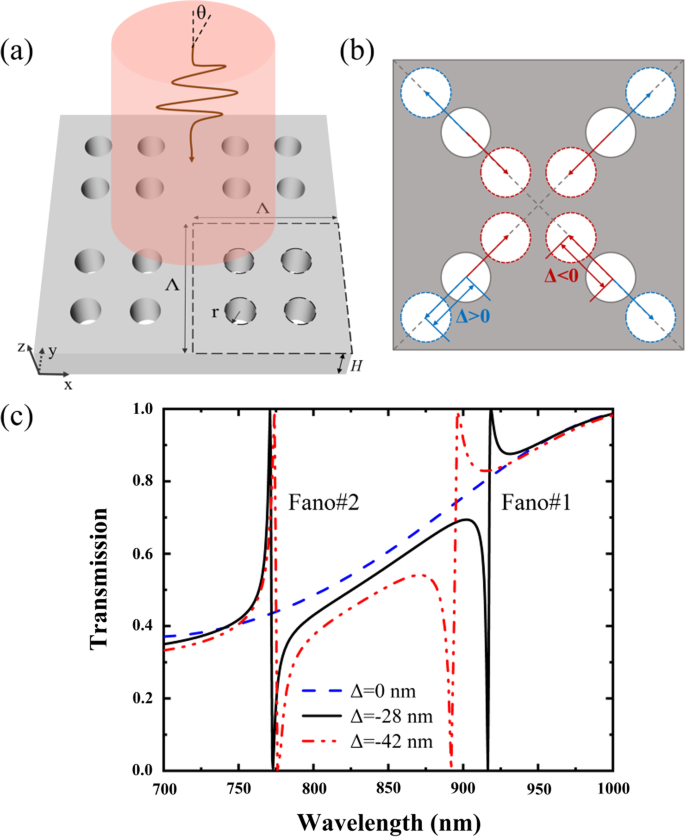
un Vista en perspectiva del SNP. b Vista vertical del SNP como cuatro nanoagujeros que se encogen (Δ <0) o se expanden (Δ> 0) a lo largo de las diagonales de la superrejilla. c Espectros de transmisión del PNS en función de la distancia de desplazamiento de Δ. El PNS está iluminado por la x -onda incidente polarizada con el ángulo de incidencia de θ =0. Los parámetros del PNS son:Λ =350 nm, r =35 nm y H =175 nm

Para mostrar claramente la evolución de las resonancias Fano de doble banda que surgen de la contracción o expansión de los agujeros tetramerizados, en la figura 2a se muestra el mapa 2D de transmisión del SNP en función de la distancia de desplazamiento de Δ. Como se muestra en la Fig. 2a, dos BIC se producen en la región de longitud de onda de interés como Δ =0, y un fenómeno similar de BIC duales se informó anteriormente en las estructuras de las metamembranas de doble rejilla [13] y el resonador de anillo dividido [21]. En el caso de Δ ≠ 0, las resonancias Fano de doble banda se realizan a medida que los BIC se inducen a los QBIC debido a la ruptura de la simetría del SNP, es decir, de la centrosimetría de la red simple a la cuádruple rotacional (C ₄ ) simetría de superrejilla. Además, debido a que el C ₄ La simetría del PNS se puede mantener a medida que los agujeros tetramerizados se contraen o expanden a lo largo de las diagonales de la superrejilla, los espectros de transmisión del PNS son los mismos para el mismo valor absoluto de | Δ |. En principio, la contracción o expansión de los orificios tetramerizados reduce el área de la primera zona de Brillouin del PNS a medida que la celda unitaria del PNS cambia de una red simple a una superrejilla, y el BIC protegido por simetría puede excitarse con una incidencia normal debido a la introducción de perturbaciones superficiales, así como plegamiento de la zona de Brillouin del SNP [42, 43]. Generalmente, el factor Q de un BIC protegido por simetría muestra una dependencia del cuadrado inverso del grado de asimetría δ basado en la teoría de la perturbación [21]:

donde ĸ es una constante de proporcionalidad, S es el área de una superrejilla, ω es la frecuencia angular y el parámetro de asimetría es \ (\ delta {=} \ sqrt 2 \ Delta / \ Lambda \).

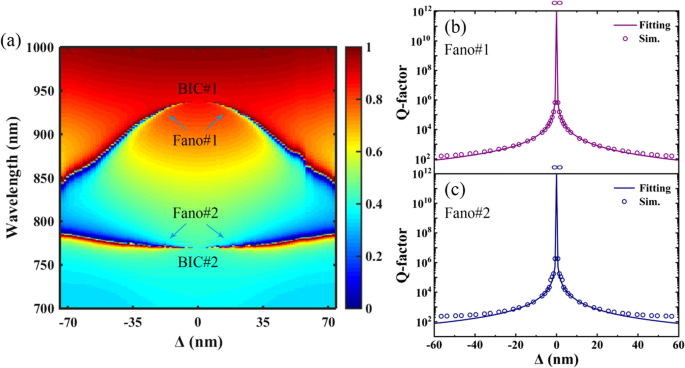
un Transmisión Mapa 2D del PNS en función de la distancia de desplazamiento de Δ a lo largo de las diagonales de la superrejilla. b y c Factor Q y el resultado de ajuste de Fano # 1 y Fano # 2, respectivamente. Otros parámetros son los mismos que en la Fig. 1c

La Figura 2b, c muestra el factor Q y el resultado de ajuste de Fano # 1 y Fano # 2, respectivamente. El factor Q del SNP se calcula como una relación entre la longitud de onda de resonancia λ _r y su ancho completo a la mitad del máximo (FWHM) Δλ, donde Δλ es la región de longitud de onda entre el pico y la caída de la resonancia Fano. Los resultados de ajuste del PNS se calculan mediante la ecuación. (1). Como se muestra en la Fig. 2b, c, las trayectorias divergentes del SNP donde los factores Q divergen hasta el infinito en Δ =0 se validan utilizando la relación del cuadrado inverso para ajustar los datos. Se pueden obtener excelentes resultados de ajuste y el ligero desacuerdo en una asimetría más grande se debe a la desviación del supuesto de una pequeña perturbación en la ecuación. (1). La ventaja significativa del PNS es que la ubicación y el factor Q de las resonancias Fano de doble banda se pueden adaptar reduciendo o expandiendo los orificios tetramerizados, lo que facilita el control dinámico de las actuaciones resonantes del múltiplo de factor Q alto. Resonancias Fano.

Mecanismos físicos e interpretación

Para obtener información sobre el origen de las resonancias Fano de doble banda mediante la reducción o expansión de los agujeros tetramerizados del PNS, descomponemos la radiación de campo lejano de la resonancia BIC y Fano en contribuciones de diferentes componentes multipolares para analizar más a fondo sus características. Los momentos multipolares se pueden calcular en función de la densidad de corriente de desplazamiento j en la superrejilla del PNS [26, 44, 45]:

donde P , M , T , Q ^{( e )} y Q ^{( m )} son los momentos de dipolo eléctrico (ED), dipolo magnético (MD), dipolo toroidal (TD), cuadrupolo eléctrico (EQ) y cuadrupolo magnético (MQ), respectivamente; c es la velocidad de la luz en el vacío y α , β = x , años , z . Aquí la densidad de carga ρ , que suele aparecer en la definición de ED y MQ, se ha reemplazado por la densidad de corriente de desplazamiento j a través de la relación de conservación de carga de \ (i \ omega \ rho + \ nabla \ cdot {\ varvec {j}} =0 \). En el caso de excitación armónica ~ exp ( iωt ), el poder de dispersión de los momentos multipolares inducidos que contribuyen a la respuesta de campo lejano se puede escribir como:

donde los dos primeros términos corresponden a la dispersión convencional ED (carga) y MD. El tercer término corresponde a la dispersión TD. El cuarto y quinto términos provienen de EQ y MQ. El último término es el término de orden superior que contiene la dispersión y el acoplamiento multipolares de orden superior entre ellos y, en general, puede ignorarse. Usando las Ecs. (2) - (7), se pueden obtener las contribuciones de diferentes multipolos al poder de dispersión del campo lejano.

La Figura 3 muestra el poder de dispersión de diferentes multipolos del PNS para diferentes distancias de desplazamiento de Δ, otros parámetros son los mismos que en la Figura 1c. Como se muestra en la Fig. 3a-d, para el SNP con Δ =0, ED y MD son los dipolos dominantes y no son resonantes en la región de longitud de onda de interés. Sin embargo, al contraer o expandir los nanoagujeros del PNS con | Δ | ≠ 0, se pueden realizar resonancias Fano de doble banda debido a las excitaciones de los modos dipolares resonantes. Para ver claramente los roles importantes de los modos de dipolo resonante en la formación de las resonancias Fano de banda dual observadas, la Fig. 3e, f muestra el poder de dispersión normalizado de diferentes multipolares con Δ =- 28 nm alrededor de Fano # 1 y Fano # 2, respectivamente . Como se muestra en la Fig. 3e, los modos de resonancia dominantes son ED y TD alrededor de Fano # 1, y Fano # 1 es la consecuencia directa del acoplamiento resonante de los dipolos toroidales eléctricos. En particular, ED y TD se mejoran fuertemente a una magnitud comparable en la punta resonante (918,5 nm) de Fano # 1; por lo tanto, se puede obtener una transmisión del 100% debido a la interferencia destructiva entre ED y TD. Mientras que para la caída resonante (916,5 nm) de Fano # 1, la reflexión se maximiza y la transmisión llega a cero debido a la dispersión mejorada de ED y TD. De manera similar, como se muestra en la Fig.3f, Fano # 2 surge del acoplamiento resonante de los dipolos toroidales magnéticos, su punta (771.1 nm) indica la interferencia destructiva entre MD y TD, mientras que su caída (772.9 nm) está asociada con el dispersión mejorada de MD y TD. Tenga en cuenta que debido al fuerte acoplamiento de dipolos toroidales eléctricos o dipolos toroidales magnéticos, los modos resonantes son robustos tanto para Fano # 1 como para Fano # 2 incluso si se varía Δ.

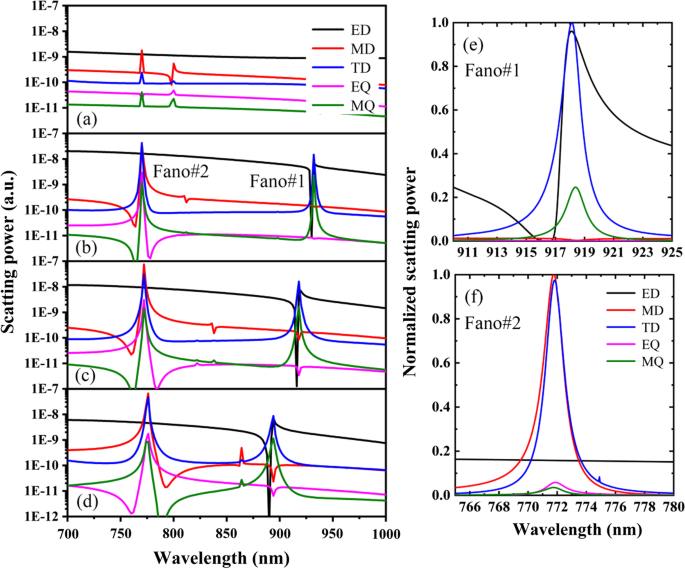
Poder de dispersión de ED, MD, TD, EQ y MQ cartesianos cuando a Δ =0, b Δ =- 14 nm, c Δ =- 28 nm y d Δ =-42 nm. e y f Poder de dispersión normalizado de diferentes multipolos con Δ =- 28 nm alrededor de Fano # 1 y Fano # 2, respectivamente. Otros parámetros son los mismos que en la Fig. 1c

Para vincular la respuesta de transmisión de las resonancias Fano de doble banda en el campo lejano con las excitaciones de los momentos multipolares inducidos, las distribuciones del campo electromagnético y la corriente de desplazamiento de las resonancias Fano de la superrejilla del SNP se muestran en la Fig. 4. Como se muestra en Fig. 4a, b, el campo eléctrico de Fano # 1 está bien confinado en la superrejilla del PNS con la corriente de desplazamiento a lo largo de x eje, que indica un modo resonante ED. Además, la corriente de desplazamiento de Fano # 1 forma dos bucles invertidos entre el centro y los bordes de la superrejilla, y el campo magnético forma un bucle en el yz plano, correspondiente a un modo de resonancia TD a lo largo de la x eje [44, 46]. Por lo tanto, Fano # 1 surge del acoplamiento resonante entre los modos ED y TD, que están en línea con los resultados predichos de las descomposiciones multipolares como se mencionó anteriormente. De hecho, debido a las características resonantes de los dipolos toroidales eléctricos de Fano # 1, las distribuciones del campo electromagnético y la corriente de desplazamiento en el pico resonante (918.5 nm), la longitud de onda central (917.5 nm) y el buzamiento resonante (916.5 nm) de Fano # 1 son casi iguales, excepto por una ligera diferencia en la amplitud del campo (archivo adicional 1:Fig. S1). En el caso de Fano # 2, como se muestra en la Fig.4c, el campo eléctrico está fuertemente mejorado y la corriente de desplazamiento forma dos bucles invertidos entre el centro de la superrejilla y la superrejilla vecina del PNS, lo que indica un modo de resonancia TD a lo largo del z eje. Además, el campo magnético de Fano # 2 está altamente localizado en la superrejilla con la dirección a lo largo de y eje, como se muestra en la Fig. 4d, con un modo resonante MD. Como resultado, Fano # 2 es la consecuencia directa del acoplamiento resonante de los dipolos toroidales magnéticos, que está de acuerdo con la predicción de las descomposiciones multipolares del campo lejano del SNP. Además, debido al acoplamiento de los dipolos toroidales magnéticos de Fano # 2, el campo electromagnético y la corriente de desplazamiento en el pico resonante (771.1 nm), la longitud de onda central (772.0 nm) y el buzamiento resonante (722.9 nm) de Fano # 2 muestran similares distribuciones (archivo adicional 1:Figura S2).

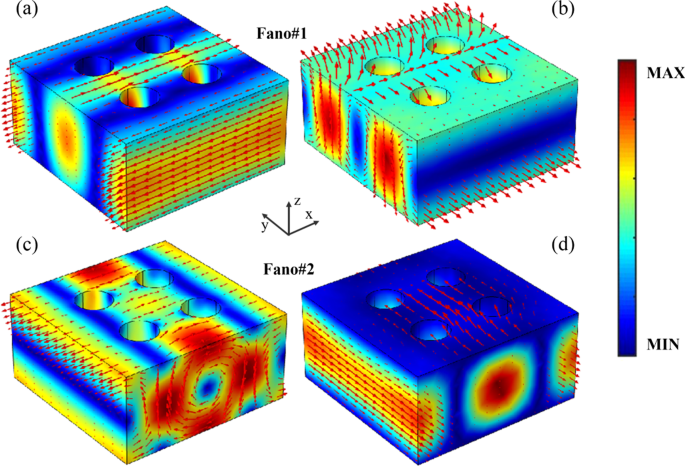
Distribuciones de campo electromagnético y corriente de desplazamiento de resonancias Fano de la superrejilla del SNP, la barra de color representa la amplitud del campo y las flechas rojas indican vector de campo o vector de corriente de desplazamiento. Otros parámetros son los mismos que en la Fig. 1c con Δ =- 28 nm. un y c Distribuciones de amplitud de campo eléctrico y vector de corriente de desplazamiento de Fano # 1 y Fano # 2, respectivamente. b y d Distribuciones de amplitud de campo magnético y vector de campo magnético de Fano # 1 y Fano # 2, respectivamente

Resultados y discusión

La figura 5 muestra los espectros de transmisión del SNP en función del radio r del nanoagujero, y otros parámetros son los mismos que en la Fig. 1c con Δ =- 28 nm. Como se muestra en la Fig. 5a, las resonancias Fano de doble banda se pueden mantener como r varía de 0 al valor máximo de 67,5 nm, es decir , los agujeros tetramerizados son tangentes entre sí en la superrejilla. El aumento del radio del nanoagujero r aumenta las perturbaciones de la superficie del SNP y también reduce su índice de refracción efectivo (ERI), lo que da como resultado el aumento del factor Q y el desplazamiento hacia el azul de las resonancias Fano. Específicamente, la ubicación resonante de Fano # 1 es más sensible a la variación de r , y las resonancias Fano de doble banda tienden a fusionarse en un modo resonante a medida que los agujeros tetramerizados se acercan entre sí. Como se muestra en la Fig. 5b, el aumento de r no solo cambia al blues la ubicación resonante de las resonancias Fano, sino que también aumenta sus FWHM. Como r aumenta de 25 a 45 nm, los picos resonantes de Fano # 1 y Fano # 2 se desplazan al azul de 936,7 nm y 793,2 nm a 887,6 nm y 743,8 nm, respectivamente; y sus FWHM se incrementan de 0,8 nm y 0,6 nm a 6,8 nm y 3,1 nm, respectivamente. Tenga en cuenta el aumento de r también mejora las profundidades de modulación de las resonancias Fano, y las profundidades de modulación al 100% se pueden realizar como r es mayor de 30 nm. Además, al evaluar el desplazamiento de la longitud de onda del pico de Fano afectado por los parámetros estructurales del SNP, se muestra que el radio del nanoagujero r es el parámetro estructural más sensible para Fano # 1 y Fano # 2 (archivo adicional 1:Figura S3). Por lo tanto, la variación de r proporciona un enfoque eficaz para controlar dinámicamente las actuaciones resonantes de las resonancias Fano de doble banda del PNS.

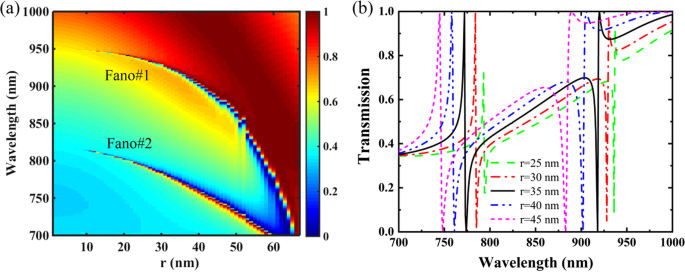
un Transmisión Mapa 2D del SNP en función del radio r del nanoagujero. b Espectros de transmisión del PNS para diferentes radios de nanoagujeros r . Otros parámetros son los mismos que en la Fig. 1c con Δ =- 28 nm

La Figura 6 muestra las influencias de la simetría de la estructura en las respuestas de transmisión del SNP, donde el radio r ' de dos nanoagujeros varía de cero a tangente entre sí, y otros parámetros son los mismos que en la Fig. 1c con Δ =- 28 nm. Como se muestra en la Fig. 6a, para la superrejilla con simetría especular a lo largo de la x eje (dirección del campo eléctrico de la luz incidente), como el radio r ′ De los dos nanoagujeros aumenta, las ubicaciones resonantes de las resonancias Fano de doble banda se desplazan hacia el azul debido a la disminución del ERI del PNS, y sus anchos de banda se amplían debido al aumento de las perturbaciones de la superficie. Sin embargo, como se muestra en la Fig. 6b, aunque las dos resonancias Fano se pueden mantener con el aumento de r ′, Se producirán dos resonancias Fano adicionales como la simetría especular de la superrejilla a lo largo de la x El eje está roto. En general, romper la simetría estructural a lo largo de la x ( y ) también romperá la simetría del modo a lo largo de la x ( y ) eje de una red periódica, y el modo no radiativo no degenerado es capaz de acoplarse a la radiación exterior debido a su componente degenerado [47]. Por lo tanto, el hecho de que las dos resonancias de Fano adicionales estén presentes solo para la estructura con simetría de espejo rota a lo largo de x El eje indica que se deben a los modos no degenerados perturbados.

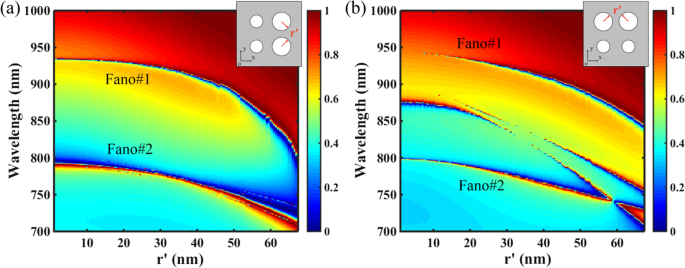
Influencias de la simetría de la estructura en las respuestas de transmisión del SNP. Otros parámetros son los mismos que en la Fig. 1c con Δ =- 28 nm. Las figuras de inserción indican el diagrama esquemático de la superrejilla del SNP. un Transmisión Mapa 2D del SNP en función del radio r ′ De dos nanoagujeros, donde la simetría estructural de la superrejilla a lo largo de la x se mantiene el eje. b Transmisión Mapa 2D del SNP en función del radio r ′ De dos nanoagujeros, donde la simetría estructural de la superrejilla a lo largo de la x el eje está roto

Además, caracterizamos los rendimientos resonantes del PNS bajo la influencia del ángulo de incidencia y el ángulo de polarización. Como se muestra en la Fig. 7a, las resonancias Fano de banda dual del SNP son inmunes a la variación del ángulo de polarización debido al C ₄ topología simétrica. A medida que el ángulo de polarización se modifica de 0 a 90 °, es decir, de x -polarización a y -polarización, Fano # 1 y Fano # 2 se mantienen iguales. Sin embargo, en el caso del ángulo de incidencia, como se muestra en la Fig.7b, aunque Fano # 1 también es insensible a la variación del ángulo de incidencia, Fano # 2 se desplaza al rojo cuando el ángulo de incidencia se desvía de la incidencia normal, y una resonancia de Fano adicional (Fano # 3) se produce debido a que la supresión de la degradación de la radiación del BIC protegido por simetría se cancela con una incidencia anormal. En general, este tipo de supresión de la degradación de la radiación de BIC está estrechamente relacionado con la interferencia destructiva entre los campos de radiación emitidos por dos modos de fuga contrapropagados en uno de los dos bordes de la banda de parada de las redes periódicas [48]. Tenga en cuenta que debido al fuerte acoplamiento entre Fano # 2 y Fano # 3, se puede excitar una ventana de transparencia inducida estrecha en la región cercana entre ellos.

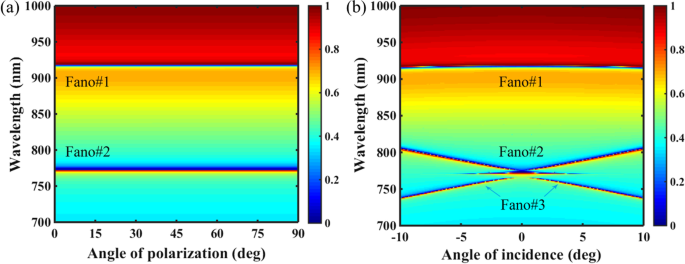
un Transmisión Mapa 2D del PNS en función del ángulo de polarización. b Transmisión Mapa 2D del SNP en función del ángulo de incidencia. Otros parámetros son los mismos que en la Fig. 1c con Δ =- 28 nm

Finalmente, mostramos que se pueden obtener múltiples resonancias de Fano aumentando la altura de la losa H del PNS. La Figura 8 muestra el mapa 2D de transmisión del SNP como funciones de H para las estructuras no encogidas (Δ =0 nm) y contraídas (Δ =- 28 nm). Como se muestra en la Fig. 8a, no hay resonancia de Fano excepto las resonancias de Fabry-Pérot (F-P) para el SNP no encogido cuando H varía. Según la teoría F – P, la condición de resonancia de la cavidad F – P del SNP no encogido se puede escribir como:

$$ \ delta =(2 \ pi / \ lambda) \ cdot H \ cdot n_ {eff} + \ varphi =m \ pi, $$ (8)

donde δ es el cambio de fase, λ es la longitud de onda en el espacio libre, n _ef es el ERI de la losa homogénea equivalente del SNP, φ es la fase adicional y m es un número entero que indica el orden de resonancia. Utilizando la teoría del medio efectivo [49], el ERI del SNP se puede estimar como:

$$ n_ {eff} =\ sqrt {\ frac {{\ left [{\ left ({1 - f} \ right) n_ {a} ^ {2} + fn_ {s} ^ {2}} \ right] \ left [{fn_ {a} ^ {2} + \ left ({1 - f} \ right) n_ {s} ^ {2}} \ right] + n_ {s} ^ {2}}} {{2 \ left [{fn_ {a} ^ {2} + \ left ({1 - f} \ right) n_ {s} ^ {2}} \ right]}}}, $$ (9)

donde f es el factor de llenado del SNP, y f =1 - 4π ( r / Λ) ² .

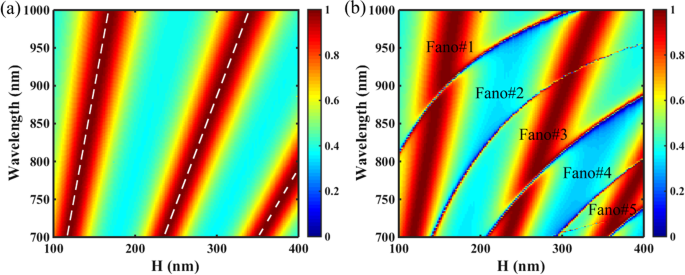
un Transmisión Mapa 2D del PNS en función de la altura de la losa H con Δ =0 nm, las líneas discontinuas blancas son los resultados del modelo de cavidad F – P. b Transmisión Mapa 2D del PNS en función de la altura de la losa H con Δ =- 28 nm. Otros parámetros son los mismos que en la Fig. 1c

Usando las Ecs. (8) y (9), las ubicaciones de la resonancia F – P del SNP no encogido se pueden calcular como λ _{F – P} =2 π · H · n _ef / ( mπ - φ ). En cálculo, aunque la fase adicional φ no puede tratarse como una constante porque evidentemente afecta el cambio de fase δ , sus valores se pueden calcular utilizando el método de ajuste lineal [50, 51]. La Figura 8a muestra el mapa 2D de transmisión del SNP con Δ =0 nm, y los resultados de la teoría F – P están indicados por las líneas discontinuas blancas. Como se muestra en la Fig. 8a, las líneas discontinuas blancas del modelo de cavidad F – P coinciden con las de los picos de transmisión del SNP, lo que confirma que es la resonancia F – P la que mejora la transmisión del SNP no encogido en el región espectral de interés. Sin embargo, como se muestra en la Fig. 8b, para el SNP contraído con Δ =- 24 nm, cinco resonancias Fano con factor Q alto se excitan y coexisten con las resonancias F – P cuando H varía en el rango de 100 a 400 nm. , las resonancias Fano son tan fuertes que dividen las resonancias F – P en la región de cruce entre las resonancias Fano y F – P. De acuerdo con la teoría de la guía de ondas de losa, el aumento en el espesor de la losa de cristal fotónico asegura más modos de fugas delimitados en la estructura [32, 52]; por tanto, el número de resonancias de Fano puede aumentarse simplemente aumentando el grosor del PNS. Tenga en cuenta que el desplazamiento de los agujeros tetramerizados no cambiará el ERI del PNS, por lo que las ubicaciones de las resonancias F – P se mantienen casi iguales para las estructuras encogidas y no encogidas.

Conclusiones

Las resonancias Fano de doble banda de factor Q alto se pueden realizar mediante el uso de una arquitectura relativamente simple de PNS basada en la excitación de QBIC duales. Al contraer o expandir cuatro nanoagujeros del SNP a lo largo de las diagonales de la superrejilla, dos BIC protegidos por simetría se pueden transformar en resonancias Fano de doble banda y sus ubicaciones, así como sus factores Q, se pueden sintonizar de manera flexible. Las resonancias Fano de banda dual del SNP son el resultado de los acoplamientos resonantes entre los dipolos toroidales eléctricos o los dipolos toroidales magnéticos, y se verifican sus correlaciones entre las múltiples descomposiciones de campo lejano y las distribuciones de campo cercano de la superrejilla. Las resonancias Fano de doble banda del PNS poseen una característica independiente de la polarización, y sus características de alto factor Q son robustas a las variaciones de los parámetros geométricos. Al aumentar la altura del PNS, se puede mejorar el número de resonancias Fano de factor Q alto, ya que la estructura puede soportar más modos con fugas. Nuestros resultados brindan más libertades de ajuste para la realización de resonadores de alto factor Q con mejores rendimientos, lo que puede proporcionar un paso más en el desarrollo de fotónica láser, de detección y no lineal.

Disponibilidad de datos y materiales

Los conjuntos de datos utilizados y / o analizados durante el estudio actual están disponibles del autor correspondiente a solicitud razonable.

Abreviaturas

factor Q:

Factor de calidad

PNS:

Losa plana con nanoagujeros

BIC:

Estados ligados en el continuo

NIR:

Infrarrojo cercano

QBIC:

Cuasi-BIC

FWHM:

Ancho completo a la mitad del máximo

ED:

Dipolo eléctrico

MD:

Dipolo magnético

TD:

Dipolo toroidal

EQ:

Cuadrupolo eléctrico

MQ:

Cuadrupolo magnético

ERI:

Índice de refracción efectivo

F – P:

Fabry – Pérot

El diseño de la capa de emisión para multiplicadores de electrones Absorción de luz mejorada con plasmón en (p-i-n) células solares de nanocables GaAs de unión:un estudio de método de simulación FDTD