Prácticas recomendadas de acumulación de tolerancias

El apilamiento de tolerancias, también conocido como apilamiento de tolerancias, se refiere a la combinación de varias tolerancias de dimensiones de piezas. Después de identificar una tolerancia en la dimensión de una parte , es importante probar si esa tolerancia funcionaría con la herramienta tolerancias:ya sea el extremo superior o el extremo inferior. Una pieza o ensamblaje puede estar sujeto a imprecisiones cuando sus tolerancias se apilan incorrectamente.

La importancia de las tolerancias

Las tolerancias influyen directamente en el costo y el rendimiento de un producto. Las tolerancias más estrictas hacen que una pieza mecanizada sea más difícil de fabricar y, por lo tanto, a menudo más costosa. Con esto en mente, es importante encontrar un equilibrio entre la capacidad de fabricación de la pieza, su funcionalidad y su costo.

Consejos para un apilamiento de tolerancia exitoso

Evite usar tolerancias que sean innecesariamente pequeñas

Como se indicó anteriormente, las tolerancias más estrictas conducen a un mayor costo de fabricación ya que la pieza es más difícil de fabricar. Este mayor costo a menudo se debe a la mayor cantidad de piezas desechadas que pueden ocurrir cuando se descubre que las dimensiones están fuera de tolerancia. El costo de portaherramientas de alta calidad y herramientas con tolerancias más estrictas también puede ser un gasto adicional.

Además, las tolerancias innecesariamente pequeñas darán lugar a tiempos de fabricación más prolongados, ya que se requiere más trabajo para garantizar que la pieza cumpla con criterios estrictos durante el mecanizado y después del mecanizado en el proceso de inspección.

Tenga cuidado de no sobredimensionar una pieza

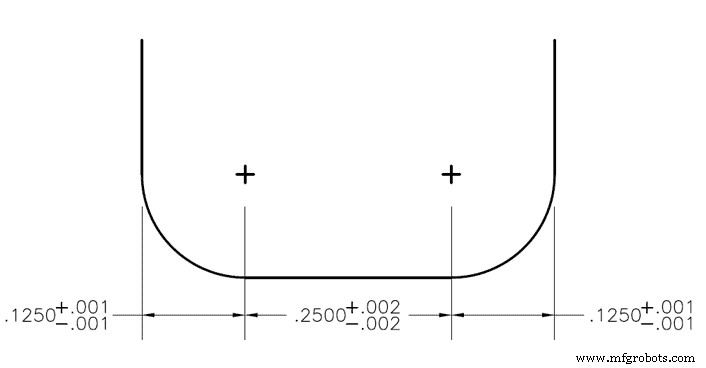
Cuando se etiqueta una tolerancia superior e inferior en cada característica de una pieza, el sobredimensionamiento puede convertirse en un problema. Por ejemplo, una fresa de extremo con radio de esquina con radios de esquina derecha e izquierda podría tener una tolerancia de +/- 0,001”, y el plano entre ellos tiene una tolerancia de 0,002”. En este caso, la ventana de tolerancia para el diámetro del cortador sería de +/- 0,004”, pero a menudo se calcula mal durante el dimensionamiento de la pieza. Además, colocar una tolerancia en esta llamada haría que se sobredimensionara y, por lo tanto, se debe dejar que la cota de referencia "REF" ocupe el lugar de la tolerancia.

Utilizar análisis de tolerancia estadística:

El análisis estadístico analiza la probabilidad de que las tres tolerancias estén por debajo o por encima del ancho de ranura dimensionado, en función de una desviación estándar. Esta probabilidad está representada por una función de densidad de probabilidad normal, que se puede ver en la figura 2 a continuación. Al combinar todas las probabilidades de las diferentes partes y dimensiones en un diseño, podemos determinar la probabilidad de que una parte tenga un problema o falle por completo, según las dimensiones y la tolerancia de las partes. Generalmente, este método de análisis solo se usa para ensamblajes con cuatro o más tolerancias.

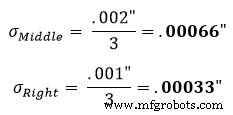
Antes de iniciar un análisis de tolerancia estadístico, debe calcular o elegir un factor de distribución de tolerancia. La distribución estándar es 3 . Esto significa que la mayoría de los datos (o, en este caso, las tolerancias) estarán dentro de las 3 desviaciones estándar de la media. Las desviaciones estándar de todas las tolerancias deben dividirse por este factor de distribución de tolerancia para normalizarlas de una distribución de 3 a una distribución de 1 . Una vez hecho esto, se puede tomar la raíz de la suma al cuadrado para encontrar la desviación estándar del ensamblaje.

Piense en ello como una taza de café preparada con 3 granos de diferentes tamaños. Para hacer una deliciosa taza de café, primero debe moler todos los granos al mismo tamaño para que puedan agregarse al filtro de café. En este caso, los granos son las desviaciones estándar, el molinillo es el factor de distribución de tolerancia y el filtro de café es la ecuación de suma de raíces al cuadrado. Esto es necesario porque algunas tolerancias pueden tener diferentes factores de distribución según la estrechez del rango de tolerancia.

El método de análisis estadístico se usa si existe el requisito de que la ranura debe tener un ancho de 0,500" con una tolerancia de +/- 0,003", pero no se necesitan los radios (0,125") y el plano (0,250"). ) para ser exactos, siempre que encajen en la ranura. En este ejemplo, tenemos 3 tolerancias bilaterales con sus desviaciones estándar ya disponibles. Dado que son bilaterales, la desviación estándar de la media sería simplemente cualquiera que sea el valor de tolerancia + o –. Para los radios exteriores, sería 0,001” y para la región plana media, sería 0,002”.

Para este ejemplo, encontremos la desviación estándar (σ) de cada sección usando la ecuación 1. En esta ecuación representa la desviación estándar.

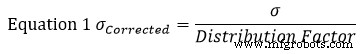
La suposición estándar es que una tolerancia parcial representa una distribución normal de +/- 3. Por lo tanto, el factor de distribución será 3. Usando la ecuación 1 en la sección izquierda de la figura 1, encontramos que su desviación estándar corregida equivale a:

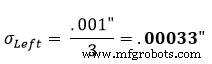
Esto luego se repite para las secciones central y derecha:

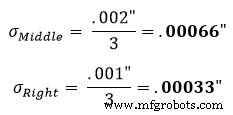
Después de llegar a estas desviaciones estándar, ingresamos los resultados en la ecuación 2 para encontrar la desviación estándar de la zona de tolerancia. La ecuación 2 se conoce como la ecuación de suma de raíces al cuadrado.

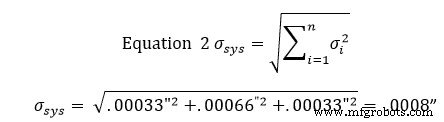
En este punto, significa que el 68 % de las ranuras estarán dentro de una tolerancia de +/- 0,0008”. Multiplicar esta tolerancia por 2 dará como resultado una ventana de confianza del 95 %, mientras que multiplicarla por 3 dará como resultado una ventana de confianza del 99 %.

El 68 % de las ranuras estarán dentro de +/- 0,0008”

El 95% de las ranuras estarán dentro de +/- .0016”

El 99% de las ranuras estarán dentro de +/- .0024”

Estas ventanas de confianza son estándar para un conjunto normal distribuido de puntos de datos. En la Figura 2 anterior se puede ver una distribución normal estándar.

El análisis de tolerancia estadística solo debe usarse para ensamblajes con más de 4 piezas con tolerancia. Muchos factores no se tuvieron en cuenta en este simple análisis. Este ejemplo fue para 3 dimensiones bilaterales cuyas tolerancias eran representativas de sus desviaciones estándar de sus medias. En el análisis de tolerancia estadística estándar, entran en juego otras variables, como ángulos, descentramiento y paralelismo, que requieren factores de corrección.

¿Sabía que las marcas de Harvey Performance Company se asocian con los principales proveedores de software de cámara de la industria para ofrecer bibliotecas de herramientas?

Haga clic aquí para obtener más información

Usar análisis de peor caso:

El análisis del peor de los casos es la práctica de sumar todas las tolerancias de una pieza para encontrar la tolerancia total de la pieza. Al realizar este tipo de análisis, cada tolerancia se establece en su límite más grande o más pequeño en su rango respectivo. Esta tolerancia total se puede comparar con los límites de rendimiento de la pieza para asegurarse de que el ensamblaje esté diseñado correctamente. Por lo general, esto se usa solo para 1 dimensión (solo 1 plano, por lo tanto, no hay ángulos involucrados) y para ensamblajes con una pequeña cantidad de piezas.

El análisis del peor de los casos también se puede utilizar al elegir la herramienta de corte adecuada para su trabajo, ya que la tolerancia de la herramienta se puede agregar a la tolerancia de las piezas para el peor de los casos. Una vez que se identifica este escenario, el maquinista o el ingeniero pueden realizar los ajustes necesarios para mantener la pieza dentro de las dimensiones especificadas en la impresión. Cabe señalar que el peor de los casos rara vez ocurre en la producción real. Si bien estos análisis pueden ser costosos para la fabricación, brindan tranquilidad a los maquinistas al garantizar que todos los ensamblajes funcionarán correctamente. A menudo, este método requiere tolerancias estrictas porque la acumulación total en condiciones máximas es la característica principal utilizada en el diseño. Las tolerancias más estrictas intensifican los costos de fabricación debido a la mayor cantidad de raspado, el tiempo de producción para la inspección y el costo de las herramientas utilizadas en estas piezas.

Ejemplo del peor de los casos en el contexto de la Figura 1:

Encuentre el límite de especificación inferior.

Para el radio de la esquina izquierda

.125” – .001” =.124”

Para la sección plana

.250” – .002” =.248”

Para el radio de la esquina derecha

.125” – .001” =.124”

Agregue todos estos juntos al límite de especificación inferior:

.124” + .248” + .124” =.496”

Encuentre el límite de especificación superior:

Para el radio de la esquina izquierda

.125” + .001” =.126”

Para la sección plana

.250” + .002” =.252”

Para el radio de la esquina derecha

.125” + .001” =.126”

Agregue todos estos juntos al límite de especificación inferior:

.126” + .252” + .126” =.504”

Reste los dos y divida esta respuesta por dos para obtener la tolerancia del peor de los casos:

(Límite superior – Límite inferior)/2 =0,004”

Por lo tanto, el peor de los casos de esta tragamonedas es .500” +/- .004”.