Reglas booleanas para simplificar

El álgebra de Boole encuentra su uso más práctico en la simplificación de circuitos lógicos.

Si traducimos la función de un circuito lógico en forma simbólica (booleana) y aplicamos ciertas reglas algebraicas a la ecuación resultante para reducir el número de términos y / o operaciones aritméticas, la ecuación simplificada se puede traducir nuevamente a la forma de circuito para un circuito lógico que funcione la misma función con menos componentes.

Si se puede lograr una función equivalente con menos componentes, el resultado será una mayor confiabilidad y un menor costo de fabricación.

Con este fin, hay varias reglas del álgebra booleana presentadas en esta sección para su uso en la reducción de expresiones a sus formas más simples.

Las identidades y propiedades ya revisadas en este capítulo son muy útiles en la simplificación booleana y, en su mayor parte, tienen similitudes con muchas identidades y propiedades del álgebra "normal".

Sin embargo, las reglas que se muestran en esta sección son exclusivas de las matemáticas booleanas.

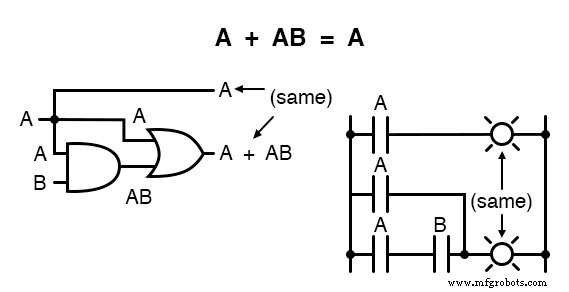
Esta regla puede probarse simbólicamente factorizando una "A" de los dos términos, luego aplicando las reglas de A + 1 =1 y 1A =A para lograr el resultado final:

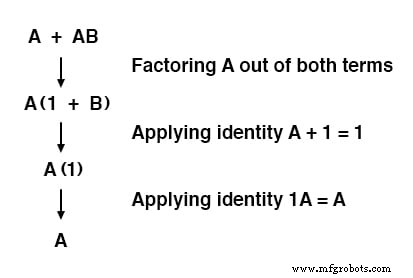
Tenga en cuenta cómo se utilizó la regla A + 1 =1 para reducir el término (B + 1) a 1.

Cuando una regla como "A + 1 =1" se expresa con la letra "A", no significa que solo se aplica a las expresiones que contienen "A".

Lo que significa la "A" en una regla como A + 1 =1 es cualquier variable booleana o colección de variables.

Este es quizás el concepto más difícil de dominar para los nuevos estudiantes en la simplificación booleana:aplicar identidades, propiedades y reglas estandarizadas a expresiones que no están en forma estándar.

Por ejemplo, la expresión booleana ABC + 1 también se reduce a 1 por medio de la identidad "A + 1 =1".

En este caso, reconocemos que el término "A" en la forma estándar de la identidad puede representar el término "ABC" completo en la expresión original.

La siguiente regla es similar a la primera que se muestra en esta sección, pero en realidad es bastante diferente y requiere una prueba más inteligente:

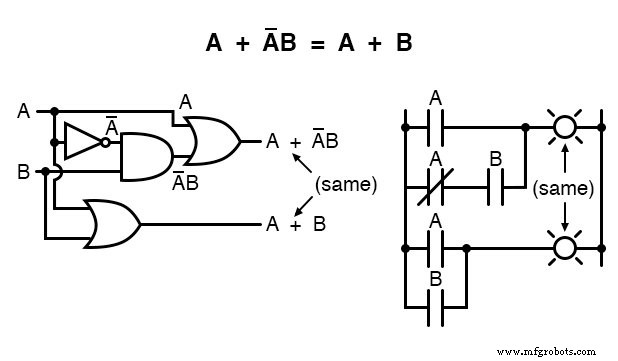
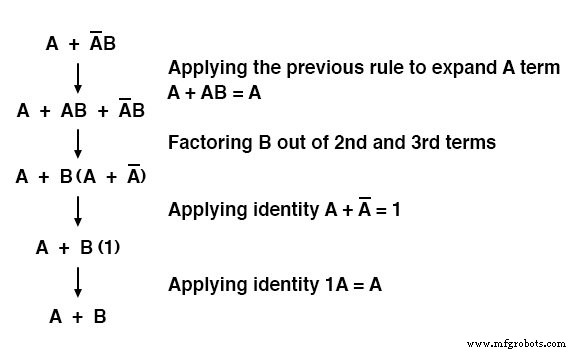
Observe cómo se usa la última regla (A + AB =A) para "des-simplificar" el primer término "A" en la expresión, cambiando la "A" por una "A + AB".

Si bien esto puede parecer un paso atrás, ¡ciertamente ayudó a reducir la expresión a algo más simple!

A veces, en matemáticas debemos dar pasos "hacia atrás" para lograr la solución más elegante.

Saber cuándo dar ese paso y cuándo no hacerlo es parte del arte del álgebra, al igual que una victoria en una partida de ajedrez casi siempre requiere sacrificios calculados.

Otra regla implica la simplificación de una expresión de producto de sumas:

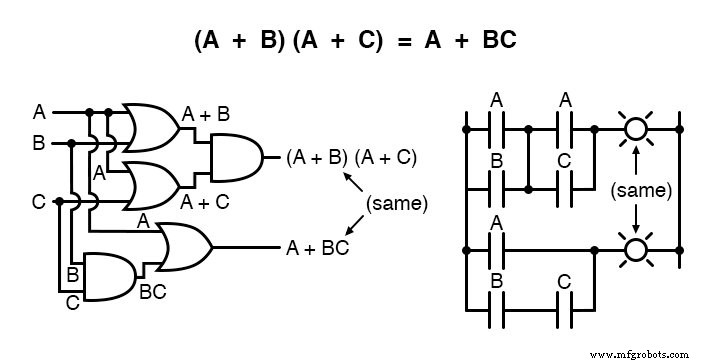
Y, la prueba correspondiente:

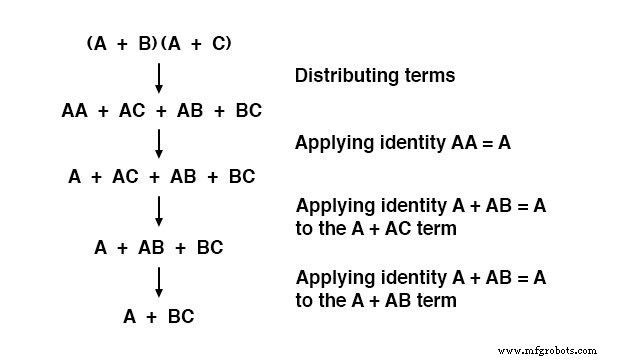
Para resumir, aquí están las tres nuevas reglas de simplificación booleana expuestas en esta sección:

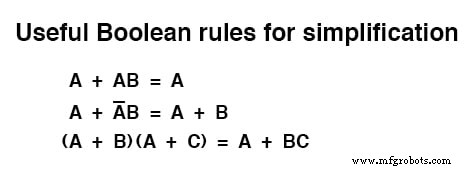
HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de álgebra booleana