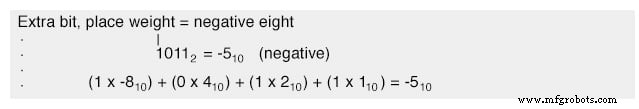Números binarios negativos

Como la suma se logra fácilmente, podemos realizar la operación de resta con la misma técnica simplemente haciendo que uno de los números sea negativo. Por ejemplo, el problema de resta de 7 - 5 es esencialmente el mismo que el problema de suma 7 + (-5).

Como ya sabemos cómo representar números positivos en binario, todo lo que necesitamos saber ahora es cómo representar sus contrapartes negativas y podremos restar.

Por lo general, representamos un número decimal negativo colocando un signo menos directamente a la izquierda del dígito más significativo, como en el ejemplo anterior, con -5. Sin embargo, el propósito de usar la notación binaria es construir circuitos de encendido / apagado que puedan representar valores de bits en términos de voltaje (2 valores alternativos:“alto” o “bajo”).

En este contexto, no podemos darnos el lujo de un tercer símbolo como un signo "menos", ya que estos circuitos solo pueden estar encendidos o apagados (dos estados posibles). Una solución es reservar un bit (circuito) que no hace más que representar el signo matemático:

Como puede ver, debemos tener cuidado cuando comenzamos a usar bits para cualquier propósito que no sea valores ponderados por lugar estándar. De lo contrario, 1101 ₂ podría malinterpretarse como el número trece cuando en realidad queremos representar cinco menos.

Para mantener las cosas claras aquí, primero debemos decidir cuántos bits se necesitarán para representar los números más grandes con los que trataremos, y luego asegurarnos de no exceder la longitud del campo de bits en nuestras operaciones aritméticas.

Para el ejemplo anterior, me he limitado a la representación de números de menos siete (1111 ₂ ) a siete positivo (0111 ₂ ), y no más, haciendo que el cuarto bit sea el bit de "signo". Solo estableciendo primero estos límites puedo evitar la confusión de un número negativo con un número positivo más grande.

Representar cinco menos como 1101 ₂ es un ejemplo del sistema signo-magnitud de numeración binaria negativa. Al usar el bit más a la izquierda como indicador de signo y no como valor ponderado por lugar, estoy sacrificando la forma "pura" de notación binaria por algo que me da una ventaja práctica:la representación de números negativos.

El bit más a la izquierda se lee como el signo, ya sea positivo o negativo, y los bits restantes se interpretan de acuerdo con la notación binaria estándar:de izquierda a derecha, coloque los pesos en múltiplos de dos.

Complementación

Tan simple como es el enfoque de magnitud de signo, no es muy práctico para propósitos aritméticos. Por ejemplo, ¿cómo agrego un cinco negativo (1101 ₂ ) a cualquier otro número, utilizando la técnica estándar para la suma binaria?

Tendría que inventar una nueva forma de hacer sumas para que funcione, y si hago eso, también podría hacer el trabajo con la resta a mano; No hay ninguna ventaja aritmética en el uso de números negativos para realizar la resta mediante la suma si tenemos que hacerlo con numeración de magnitud de signo, ¡y ese era nuestro objetivo!

Hay otro método para representar números negativos que funciona con nuestra técnica conocida de la suma a mano, y también tiene más sentido desde el punto de vista de la numeración ponderada por lugar, llamada complementación.

Con esta estrategia, asignamos el bit más a la izquierda para que tenga un propósito especial, tal como lo hicimos con el enfoque de magnitud de signo, definiendo nuestros límites numéricos como antes. Sin embargo, esta vez, el bit más a la izquierda es más que un bit de signo; más bien, posee un valor posicional negativo. Por ejemplo, un valor de cinco menos se representaría como tal:

Con los tres bits de la derecha capaces de representar una magnitud de cero a siete, y el bit más a la izquierda representando cero o menos ocho, podemos representar con éxito cualquier número entero de menos siete (1001 ₂ =-8 ₁₀ + 1 ₂ =-7 ₁₀ ) a siete positivo (0111 ₂ =0 ₁₀ + 7 ₁₀ =7 ₁₀ ).

Representar números positivos en este esquema (con el cuarto bit designado como peso negativo) no es diferente de la notación binaria ordinaria. Sin embargo, representar números negativos no es tan sencillo:

Tenga en cuenta que los números binarios negativos en la columna de la derecha, que son la suma del total de los tres bits de la derecha más el ocho negativo del bit más a la izquierda, no "cuentan" en la misma progresión que los números binarios positivos en la columna de la izquierda.

Más bien, los tres bits de la derecha deben establecerse en el valor adecuado para igualar el total deseado (negativo) cuando se suman con el valor de posición negativo de ocho del bit más a la izquierda.

Complemento de dos

Los tres bits de la derecha se conocen como el complemento a dos del número positivo correspondiente. Considere la siguiente comparación:

En este caso, siendo el bit de peso negativo el cuarto bit (valor posicional de ocho negativo), el complemento a dos para cualquier número positivo será el valor que se necesite sumar al ocho negativo para hacer el equivalente negativo de ese valor positivo.

Afortunadamente, existe una manera fácil de averiguar el complemento de dos para cualquier número binario:simplemente invierta todos los bits de ese número, cambiando todos los 1 por 0 y viceversa (para llegar a lo que se llama el complemento de uno) y luego agregue uno. Por ejemplo, para obtener el complemento a dos de cinco (101 ₂ ), primero invertiríamos todos los bits para obtener 010 ₂ (el "complemento a uno"), luego agregue uno para obtener 011 ₂ , o -5 ₁₀ en forma de complemento a dos de tres bits

Curiosamente, la generación del complemento a dos de un número binario funciona igual si manipula todos los bits, incluido el bit más a la izquierda (signo) al mismo tiempo que los bits de magnitud. Intentemos esto con el ejemplo anterior, convirtiendo un cinco positivo en un cinco negativo, pero realizando el proceso de complementación en los cuatro bits.

Debemos asegurarnos de incluir el bit de signo 0 (positivo) en el número original, cinco (0101 ₂ ). Primero, invirtiendo todos los bits para obtener el complemento a uno:1010 ₂ . Luego, agregando uno, obtenemos la respuesta final:1011 ₂ , o -5 ₁₀ expresado en forma de complemento a dos de cuatro bits.

Es de vital importancia recordar que el lugar del bit de peso negativo ya debe estar determinado antes de que se puedan realizar conversiones de complemento a dos. Si nuestro campo de numeración binaria fuera tal que el octavo bit fuera designado como bit de peso negativo (10000000 ₂ ), tendríamos que determinar el complemento a dos en función de los otros siete bits.

Aquí, el complemento a dos de cinco (0000101 ₂ ) sería 1111011 ₂ . Un cinco positivo en este sistema se representaría como 00000101 ₂ y un cinco negativo como 11111011 ₂ .

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de matemáticas binarias