Sistema teórico de nanogeneradores triboeléctricos en modo de contacto para una alta eficiencia de conversión de energía

Resumen

Con la rápida expansión de la electrónica de próxima generación, las fuentes de energía portátiles y eficientes se han convertido en uno de los factores más importantes que obstaculizan el desarrollo del mercado. Los nanogeneradores triboeléctricos (TENG) son un candidato potencial por sus características insuperables. Aquí, analizamos en profundidad la potencia y la eficiencia de conversión de los TENG en modo de contacto considerando todo el proceso de conversión de energía. En primer lugar, yendo más allá del análisis convencional, se introdujo una fuerza de compresión para obtener un perfil de movimiento más versátil, lo que proporcionó una mejor comprensión del principio de funcionamiento del proceso de separación de contactos. Luego, analizamos en profundidad la influencia de varios parámetros en su desempeño. Especialmente, los TENG de máxima eficiencia se pueden obtener con una fuerza óptima. Es realista y útil para TENG más eficientes. Además, esta investigación tiene buenas posibilidades de establecer estándares para cuantificar la eficiencia de los TENG, lo que sienta las bases para una mayor industrialización y multifuncionalización de la tecnología TENG.

Antecedentes

La inteligencia artificial y la red en la nube están mejorando gradualmente la calidad de nuestra vida moderna con el rápido desarrollo de la electrónica de próxima generación para el hogar inteligente, el control de la salud, el entretenimiento y el control del entorno [1, 2, 3]. Alimentar estas grandes cantidades de componentes electrónicos se ha convertido en una misión imposible utilizando las tecnologías de baterías existentes, considerando su gran tamaño, corta vida útil y problemas de carga especialmente rápida. Se ha convertido en una de las barreras más importantes para desarrollar una fuente de energía sostenible adecuada para dispositivos electrónicos portátiles [4, 5, 6].

Actualmente, los nanogeneradores triboeléctricos (TENG) basados en la triboelectrificación han demostrado una tecnología atractiva para la recolección de energía mecánica. Es un candidato prometedor para dispositivos electrónicos portátiles por sus numerosas ventajas, que incluyen flexibilidad [7], rentabilidad [8], proceso de fabricación simple [9], protección del medio ambiente [10] y versatilidad [11]. Se ha utilizado ampliamente para recolectar energía de la energía mecánica ambiental. Además, se puede utilizar para integrarse con dispositivos portátiles para aplicaciones autoamplificadas [12, 13, 14]. Por ahora, se han utilizado muchos métodos para aumentar la potencia, incluida la morfología de la superficie [15, 16], la optimización del material [17, 18], la inyección de carga [19, 20], la optimización de la estructura [21, 22] y los nanogeneradores múltiples. [23, 24]. A pesar del rápido avance en el rendimiento de la producción, no existe un modelo definitivo para analizar la eficiencia de conversión de energía. Se han publicado varias explicaciones teóricas para diferentes modos de TENG [25, 26, 27]. Sin embargo, la mayoría de los análisis no discuten todo el proceso de conversión de energía y solo se enfocan en la potencia de salida. Más importante aún, una mayor potencia de salida no significa una mayor eficiencia de conversión de energía e incluso puede resultar contraproducente. De alguna manera ha impedido el desarrollo de TENG más eficientes debido a la falta de un estudio directo sobre la eficiencia de conversión de energía.

En este trabajo, analizamos de manera sistémica y directa la potencia y la eficiencia de conversión de los TENG en modo contacto considerando todo el proceso. En primer lugar, yendo más allá del análisis convencional, se introdujo una fuerza de compresión para obtener un perfil de movimiento más versátil, lo que proporcionó una mejor comprensión del principio de funcionamiento del proceso de separación de contactos. Luego, de acuerdo con las ecuaciones de movimiento, se presentaron ecuaciones explícitas para el importante desempeño del dispositivo en todo el proceso de contacto y separación. Finalmente, se investigó sistemáticamente la influencia de las propiedades de los materiales, los parámetros estructurales y el factor experimental en la potencia máxima y especialmente en la eficiencia de conversión de energía. Podemos obtener la máxima eficiencia y potencia mediante el diseño racional de parámetros, especialmente la fuerza de compresión. Es realista y útil para TENG más eficientes. Es importante destacar que tiene una buena posibilidad de establecer los estándares para cuantificar la eficiencia de los TENG, lo que sienta las bases para una mayor industrialización y multifuncionalización de los TENG.

Métodos

El principio de funcionamiento básico de los TENG se basa en la triboelectrificación y la inducción electrostática. Se podría clasificar aproximadamente en dos tipos en vista de los materiales de fricción. Debido a la función de trabajo y la fricción, el material dieléctrico y el material conductor se eligen como pares triboeléctricos. Como se muestra en la Fig. 1, la capa superior consta de un electrodo superior (TE) y la capa dieléctrica puede moverse hacia arriba y hacia abajo, mientras que el electrodo inferior (BE) está fijo en el sustrato. Las dos capas están conectadas con una resistencia de carga R . El proceso de separación y contacto se indican en la Fig. 1a, b, respectivamente. En el proceso de separación, los electrones fluyen al BE desde el TE y regresan al TE en el proceso de contacto.

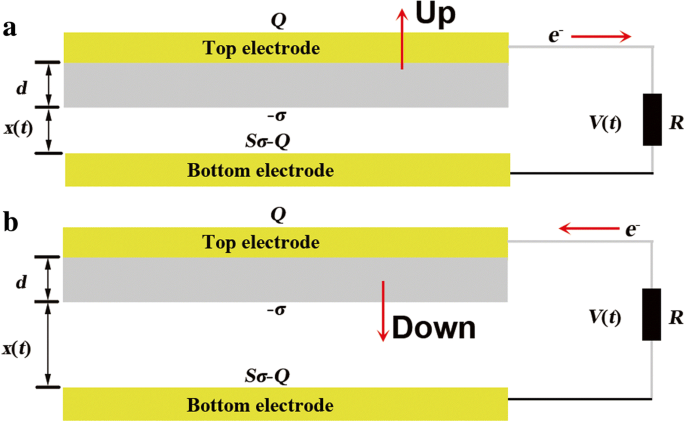
El modelo teórico para el modo de contacto de TENGA. un Proceso de separación y b proceso de contacto

Bajo la fuerza aplicada F , la capa superior hará contacto completo con la capa inferior. El BE tendrá cargas triboeléctricas positivas con la densidad de carga superficial σ mientras que la capa dieléctrica tiene las mismas cargas con signo opuesto. En el proceso de separación, la capa superior se separa con la capa inferior con una distancia x ( t ). Dará como resultado una diferencia de potencial V ( t ) entre el TE y BE debido al campo eléctrico. Para compensar V ( t ), los electrones fluirán entre los dos electrodos a través de R . Por lo tanto, las cargas del TE son Q mientras que el BE se queda con Sσ - Q . La intensidad del campo eléctrico en las dos regiones se da de la siguiente manera de acuerdo con el teorema de Gauss.

Dentro de la capa dieléctrica:

$$ {E} _ {\ mathrm {dieléctrico}} =- \ frac {Q} {S {\ varepsilon} _0 {\ varepsilon} _r} $$ (1)

Dentro del espacio de aire:

$$ {E} _ {\ mathrm {air}} =\ frac {\ sigma_0-Q / S} {\ varepsilon_0} $$ (2)

donde ε ₀ y ε _r son la permitividad del vacío y la permitividad relativa, respectivamente.

La V ( t ) debe satisfacer la siguiente ecuación:

$$ V (t) ={E} _ {\ mathrm {dieléctrico}} d + {E} _ {\ mathrm {aire}} x (t) $$ (3)

De la ley de Ohm, la V ( t ) se da como

$$ V (t) =RI (t) =R \ frac {dQ} {dt} $$ (4)

Fusionando ecuaciones, podemos obtener

$$ \ frac {dQ} {dt} + \ frac {d_0 + x (t)} {RS {\ varepsilon} _0} \ times Q =\ frac {\ sigma x (t)} {R {\ varepsilon} _0 } $$ (5)

La Eq. (5) es la ecuación que rige los TENG. Puede aplicarse a todo el proceso de separación y contacto. Es obvio que x ( t ) es uno de los factores más importantes de los TENG. A diferencia del trabajo anterior, construimos la ecuación de movimiento práctica en lugar de asumirla directamente. En este artículo, la ecuación de movimiento en todo el proceso se construye en base a la fuerza de compresión y la condición experimental.

Resultados y discusión

Sistema sin resorte

En primer lugar, solo consideramos una fuerza de compresión constante F y la gravedad de la capa superior. La ecuación de movimiento se puede obtener de la siguiente manera (consulte el archivo adicional 1:Nota 1 y Figura S1 en el ESM). En realidad, el x ( t ) siempre tiene un valor máximo x _máx y mínimo cero. Entonces las ecuaciones de movimiento vienen dadas por

$$ \ left \ {\ begin {array} {c} \ x (t) =\ frac {F- mg} {2m} {t} ^ 2, t <\ sqrt {\ frac {2 {x} _ { \ mathrm {max}} m} {F- mg}} \ \\ {} x (t) ={x} _ {\ mathrm {max}}, t \ ge \ sqrt {\ frac {2 {x} _ {\ mathrm {max}} m} {F- mg}} \ end {matriz} \ right. $$ (6.1) $$ \ left \ {\ begin {array} {c} \ x (t) =\ frac {F + mg} {2m} {t} ^ 2, t <\ sqrt {\ frac {2 { x} _ {\ mathrm {max}} m} {F + mg}} \ \\ {} x (t) =0, t \ ge \ sqrt {\ frac {2 {x} _ {\ mathrm {max}} m} {F + mg}} \ end {matriz} \ right. $$ (6.2)

Las Ecs. (6.1) y (6.2) representan el proceso de separación y el proceso de contacto, respectivamente.

Entonces podemos obtener el cargo transferido. (La derivación detallada se encuentra en el archivo adicional 1:Nota 2 del ESM).

En el proceso de separación:

$$ {\ Displaystyle \ begin {array} {l} Q (t) =\ exp \ left (- \ frac {6m {d} _0t + \ left (F- mg \ right) {t} ^ 3} {6 mRS {\ varepsilon} _0} \ right) \\ {} \ times {\ int} _0 ^ t \ frac {\ sigma \ left (F- mg \ right) {t} ^ 2} {2 mR {\ varepsilon} _0 } \ mathit {\ exp} \ frac {6m {d} _0t + \ left (F- mg \ right) {t} ^ 3} {6 mRS {\ varepsilon} _0} dt, t <\ sqrt {\ frac {2 {x} _ {\ mathrm {max}} m} {F- mg}} \ end {matriz}} $$ (7.1) $$ {\ Displaystyle \ begin {array} {l} Q (t) =\ frac {\ sigma S {x} _ {\ mathrm {max}}} {d_0 + {x} _ {\ mathrm {max}}} - \ left (\ frac {\ sigma S {x} _ {\ mathrm {max} }} {d_0 + {x} _ {\ mathrm {max}}} - {Q} _0 \ right) \\ {} \ times \ mathit {\ exp} \ left (- \ frac {d_0 + {x} _ {\ mathrm {max}}} {RS {\ varepsilon} _0} \ left (t- {t} _0 \ right) \ right), t \ ge \ sqrt {\ frac {2 {x} _ {\ mathrm {max} } m} {F- mg}} \ end {matriz}} $$ (7.2)

donde \ ({t} _0 =\ sqrt {2 {x} _ {\ mathrm {max}} m / \ left (F- mg \ right)} \) y Q ₀ = Q ( t ₀ ) en la ecuación. (7.1).

En el proceso de contacto:

$$ {\ Displaystyle \ begin {array} {l} Q (t) =\ exp \ left (- \ frac {6m {d} _0t + \ left (F + mg \ right) {t} ^ 3} {6 mRS { \ varepsilon} _0} \ right) \\ {} \ times \ left (\ sigma S + {\ int} _0 ^ t \ frac {\ sigma \ left (F + mg \ right) {t} ^ 2} {2 mR { \ varepsilon} _0} \ mathit {\ exp} \ frac {6m {d} _0t + \ left (F + mg \ right) {t} ^ 3} {6 mRS {\ varepsilon} _0} dt \ right), t <\ sqrt {\ frac {2 {x} _ {\ mathrm {max}} m} {F + mg}} \ end {array}} $$ (8.1) $$ Q (t) ={Q} _0 \ times \ exp \ left (\ frac {d_0 {t} _0- {d} _0t} {RS {\ varepsilon} _0} \ right), t \ ge \ sqrt {\ frac {2 {x} _ {\ mathrm {max}} m} {F + mg}} $$ (8.2)

donde \ ({t} _0 =\ sqrt {2 {x} _ {\ mathrm {max}} m / \ left (F + mg \ right)} \), Q ₀ se puede calcular asignando t = t ₀ en Eq. (8.1).

Por lo tanto, la corriente de salida se puede derivar como I ( t ) = dQ / dt y V ( t ) = RI ( t ).

De acuerdo con los parámetros específicos exhibidos en la Tabla 1, podemos obtener los resultados del cálculo numérico.

La relación características-tiempo en diferentes R en todo el proceso se muestra en la Fig. 2. Las cargas transferidas, la corriente de salida y las relaciones de voltaje de salida a diferentes cargas en el proceso de contacto se muestran en la Fig. 2a, c, e. Los comportamientos son similares a los de estudios anteriores [25]. Pero el proceso de separación rara vez se estudia. Suponga que las cargas superficiales se transfieren completamente al TE en el proceso de separación después de mucho tiempo. Como se muestra en la Fig. 2b, en condición de cortocircuito (SC), las cargas en el TE pueden fluir completamente de regreso al BE cuando la capa superior deja de moverse ( t =2 ms). Los cargos no pueden disminuir a cero en t =2 ms cuando R es más de 1 MΩ. Considerando que, casi todos los cargos se transfieren al BE cuando R es inferior a 10 MΩ en el proceso de separación. Las cargas transferidas en el proceso de contacto son mucho menores que las del proceso de separación. Esto se debe a la fuerza impulsora relativamente pequeña en el proceso de contacto temprano. La relación entre la corriente y el tiempo de salida se representa en la figura 2d. En condición SC, la corriente máxima es casi la misma que en el proceso de separación. Cuando R es mayor, la curva actual-tiempo tiene dos valores máximos locales, que está al principio y al final del movimiento. Y la corriente máxima absoluta cae dramáticamente a medida que aumenta la resistencia. Los dos valores máximos locales al principio y al final del movimiento se deben a los electrones adecuados y al movimiento de alta velocidad, respectivamente. El voltaje de salida tiene el mismo perfil que la corriente, pero una tendencia diferente en magnitud, como se muestra en la Fig. 2f (consulte el archivo adicional 1:Figura S2 para ver la relación detallada en el ESM). Cabe señalar que el valor de voltaje máximo absoluto es mucho menor en comparación con el del proceso de separación. Obviamente, el voltaje y la corriente no son simétricos en el proceso de separación y contacto. Combinando el proceso de separación y contacto, el voltaje y la corriente de salida se alternan.

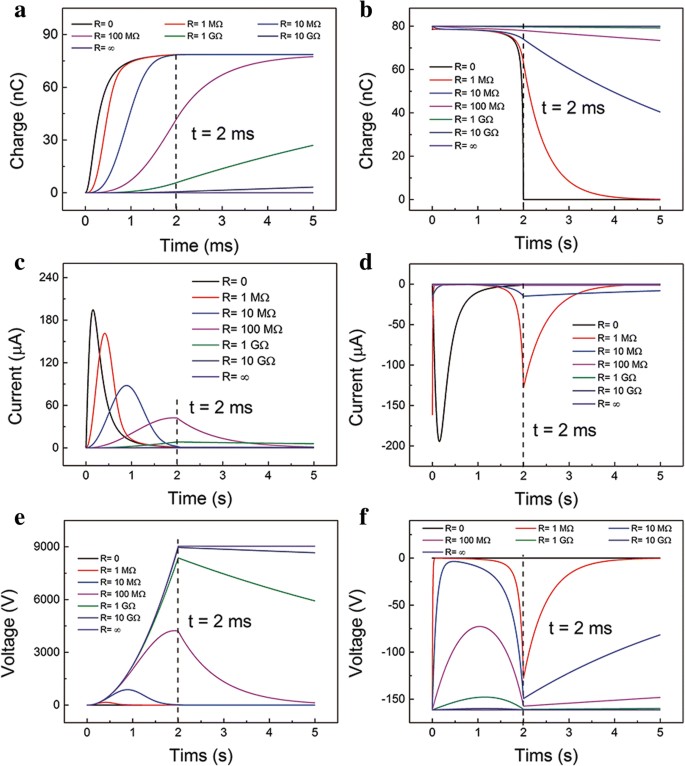
Características de salida calculadas cuando el dispositivo está bajo una fuerza de compresión constante F. Relación cargos-tiempo transferidos a diferentes R en el a proceso de contacto y b proceso de separación. Relación de tiempo actual en diferentes R en la c proceso de contacto y d proceso de separación. Relación voltaje-tiempo en diferentes R en el e proceso de contacto y f proceso de separación

Además, la influencia de varios parámetros en la relación entre la potencia máxima P _máx y la resistencia correspondiente se representan en la Fig. 3. Estos diferentes parámetros se pueden dividir en material, estructura y condición del experimento. Por ejemplo, los parámetros del material incluyen σ y ε _r . Los parámetros estructurales son principalmente el tamaño del área S, x _máx y d. La fuerza de compresión F es el parámetro de experimento. Se puede ver que σ, S , F y x _máx influyen en gran medida en la P _máx , como se muestra en la Fig. 3a – d. La P _máx aumenta drásticamente a medida que σ, S , F y x _máx aumento. El parámetro σ y S decidir principalmente la cantidad de cargos que se pueden transferir. Los parámetros F y x _máx Influyen principalmente en las ecuaciones de movimiento. La resistencia óptima correspondiente disminuye con x _máx disminuyendo mientras que rara vez se ve afectado por σ, S y F. Además, los parámetros d y ε _r rara vez afectan a la P _máx y la resistencia correspondiente, como se indica en la Fig. 3e, f. Ese es el espesor efectivo de la capa dieléctrica d ₀ = d / ε _r que tiene poca influencia en el desempeño de los TENG. Podemos ajustar estos parámetros para controlar la potencia máxima. Vale la pena señalar que la resistencia correspondiente suele ser la resistencia de carga de la electrónica.

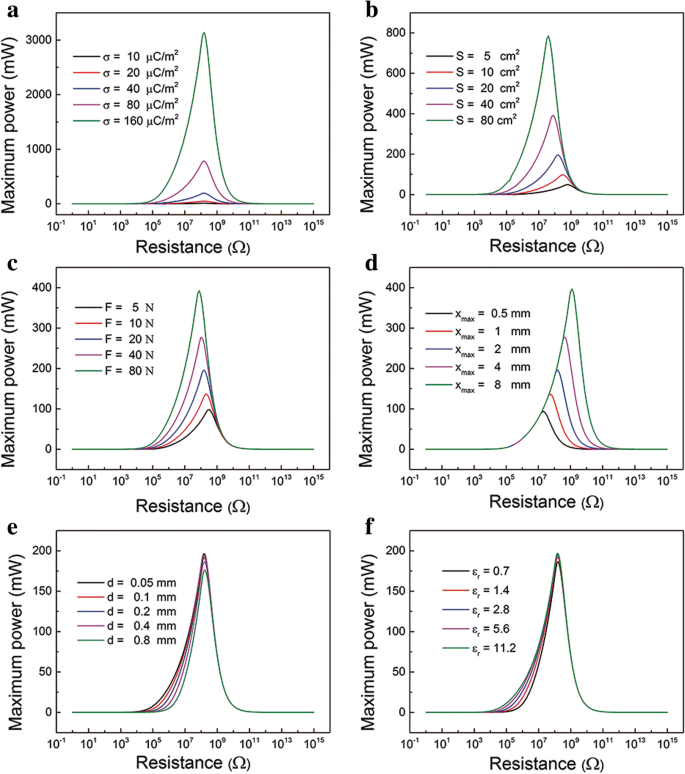
El efecto de los parámetros en P _máx y la correspondiente resistencia. Perfil de potencia instantánea con R en a diferente densidad de carga superficial σ, b tamaño del área S , c fuerza de compresión F , d distancia máxima de separación x _máx , e espesor de la capa dieléctrica d y f ε _r

Sistema Spring

Para una condición de experimento más popular, se incluye el sistema de resorte. La fuerza de compresión F se aplica periódicamente, como se muestra en la Fig. 4a. En el proceso de separación ( T = t ₁ ), solo hay fuerza de restauración de los resortes y la gravedad, por lo que F =0. Durante el proceso de contacto ( T = t ₂ + t ₃ ), la fuerza de compresión F está agregado. Y aún duraría mucho después de que las dos capas entraran en contacto total. Las curvas de movimiento se muestran en la Fig. 4b. Las ecuaciones de movimiento calculadas y el rendimiento de salida se derivan de la siguiente manera. (Archivo adicional 1:Nota 3 en el ESM)

$$ \ mathrm {x} (t) ={x} _ {\ mathrm {max}} - {x} _ {\ mathrm {max}} \ mathit {\ cos} \ left ({\ omega} _0t \ right ) $$ (9.1) $$ \ mathrm {x} (t) ={x} _ {\ mathrm {max}} - \ frac {F} {k} + \ frac {F} {k} \ cos \ left ({\ omega} _0t \ right) $$ (9.2)

donde \ ({\ omega} _0 ^ 2 =k / m \). Y las Ecs. (9.1) y (9.2) representan el proceso de separación y el proceso de contacto, respectivamente.

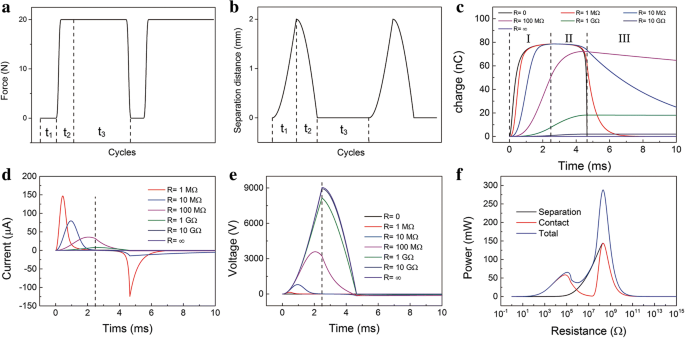
Características calculadas de los TENG en modo de separación de contactos . un La fuerza periódica F . b El movimiento periódico de la capa superior. c Relación cargos-tiempo transferidos a diferentes R en el proceso de contacto y separación. d Relación de tiempo actual en diferentes R en el proceso de contacto y separación. e Relación voltaje-tiempo en diferentes R en el proceso de contacto y separación. f Las relaciones de potencia máxima instantánea con resistencias en el contacto, separación y todo el proceso

En el proceso de separación:

$$ {\ Displaystyle \ begin {array} {c} Q (t) ={\ int} _0 ^ t \ frac {\ sigma {x} _ {\ mathrm {max}} \ left (1- \ mathit {\ cos} \ left ({\ omega} _0t \ right) \ right)} {R {\ varepsilon} _0} \ mathit {\ exp} \ left (\ frac {d_0 + {x} _ {\ mathrm {max}}} {RS {\ varepsilon} _0} t- \ frac {x _ {\ mathrm {max}}} {RS {\ varepsilon} _0 {\ omega} _0} \ mathit {\ sin} \ left ({\ omega} _0t \ derecha) \ derecha) dt \\ {} \ veces \ mathit {\ exp} \ izquierda (- \ frac {d_0 + {x} _ {\ mathrm {max}}} {RS {\ varepsilon} _0} t + \ frac { x _ {\ mathrm {max}}} {RS {\ varepsilon} _0 {\ omega} _0} \ mathit {\ sin} \ left ({\ omega} _0t \ right) \ right), t <{t} _1 \ end {array}} $$ (10)

En el proceso de contacto:

$$ {\ Displaystyle \ begin {array} {l} Q (t) =\ mathit {\ exp} \ left (- \ frac {d_0 + {x} _ {\ mathrm {max}} - \ frac {F} { k}} {RS {\ varepsilon} _0} t + \ frac {Fsin \ left ({\ omega} _0t \ right)} {kRS {\ varepsilon} _0 {\ omega} _0} \ right) \\ {} \ veces \ left \ {{q} _0 + {\ int} _0 ^ t \ mathit {\ exp} \ left (\ frac {d_0 + {x} _ {\ mathrm {max}} - \ frac {F} {k}} { RS {\ varepsilon} _0} t- \ frac {Fsin \ left ({\ omega} _0t \ right)} {kRS {\ varepsilon} _0 {\ omega} _0} \ right) \ right. \ \\ {} \ \\ {} \ times \ left. \ frac {\ sigma \ left ({x} _ {\ mathrm {max}} - \ frac {F} {k} + \ frac {F} {k} \ cos \ left ({\ omega} _0t \ right) \ right)} {R {\ varepsilon} _0} dt \ right \}, t <{t} _2 \ \ end {array}} $$ (11) $$ Q (t ) ={Q} _0 \ times \ mathit {\ exp} \ left (\ frac {d_0} {RS {\ varepsilon} _0} \ left ({t} _0-t \ right) \ right), t \ ge { t} _3 $$ (12)

donde q ₀ son los cargos que se transfirieron del BE al TE en el proceso de separación.

La corriente y el voltaje de salida se pueden calcular como I ( t ) = dQ / dt y V ( t ) = RI ( t ).

La relación cargo-tiempo transferida en diferentes R en el proceso completo se representa en la Fig. 4c. El proceso de transferencia de carga se divide en tres regiones, que corresponde a la fuerza periódica. La Región I representa el proceso de separación y el proceso de contacto contiene las regiones II y III. En la región I, los cargos se transfieren al TE desde el BE. Las cargas en el TE siguen aumentando. En la región II, la dirección del flujo de carga está relacionada con la resistencia. Las cargas en el TE continúan aumentando cuando la resistencia es grande ( R ≥ 1 GΩ). Aumenta al máximo y luego disminuye cuando la resistencia es baja ( R ≤ 100 MΩ). Especialmente, cuando R =0, los cargos continuarán disminuyendo en la región II. En la región III, los cargos en el TE continúan disminuyendo. La corriente de salida correspondiente en todo el proceso se muestra en la Fig. 4d. La corriente en el proceso de separación y contacto tiene el signo contrario. Por lo general, el valor de corriente máxima en el proceso de separación es un poco mayor que en el proceso de contacto. Curiosamente, en el proceso de contacto, el valor actual máximo absoluto aparece al comienzo del proceso de contacto o en el momento en que recién están en contacto. Cuando la resistencia es grande, aparece al inicio del proceso de contacto, y viceversa. El voltaje de salida aumenta con el tiempo y luego disminuye, como se muestra en la Fig. 4e. El voltaje de salida aparecería como un valor negativo en el proceso de contacto. Y el valor absoluto es mucho menor que el del proceso de separación. Estas cifras son consistentes con los gráficos experimentales medidos en la literatura. La corriente de salida medida es obviamente alterna, y la tensión de salida medida suele ser de pico. Las relaciones de la potencia máxima instantánea con las resistencias en el contacto, la separación y todo el proceso se muestran en la Fig. 4f. El TENG alcanza su potencia instantánea máxima absoluta alrededor de 200 MΩ en el proceso de separación y contacto. Mientras está en el proceso de contacto, tiene un valor máximo local adicional alrededor de 0.1 MΩ. Entonces, en todo el proceso, la potencia instantánea obtiene su valor máximo alrededor de 200 MΩ. Se puede ver que la curva de potencia del proceso de contacto se superpone a la del proceso de separación cuando la resistencia es grande. Porque el valor de corriente máximo aparece en la intersección de los dos procesos cuando R ≥ 200 MΩ.

Además, los resultados calculados de P _máx y la resistencia óptima correspondiente se representan en la Fig. 5. Como se indica en la Fig. 5a-c, la potencia instantánea máxima aumenta a medida que los parámetros x _máx , S y k aumento. Esto puede contribuir a una mayor velocidad de transferencia de los electrones. Al mismo tiempo, también cambia la resistencia óptima correspondiente. La resistencia óptima disminuye con S y k aumentando, pero la tendencia inversa con x _máx . La influencia de los parámetros σ en la P _máx y la resistencia óptima se muestra en la Fig. 5d. La P _máx aumenta rápidamente con el aumento de σ, mientras que la resistencia óptima se mantiene constante. La resistencia óptima tampoco se ve afectada por ε _r . Pero como ε _r aumenta, la potencia instantánea máxima aumenta y luego se satura. La F casi no tiene influencia sobre la potencia instantánea máxima y la resistencia óptima. En todo el proceso de contacto y separación, la F solo afecta el proceso de contacto. Entonces, la corriente máxima en el proceso de separación se mantiene igual. Como se ilustra en la Fig. 5f, la potencia instantánea máxima no cambia. Esto es diferente del sistema sin resorte. En el sistema sin resorte, el F afecta directamente el proceso de separación, por lo tanto afecta la potencia máxima.

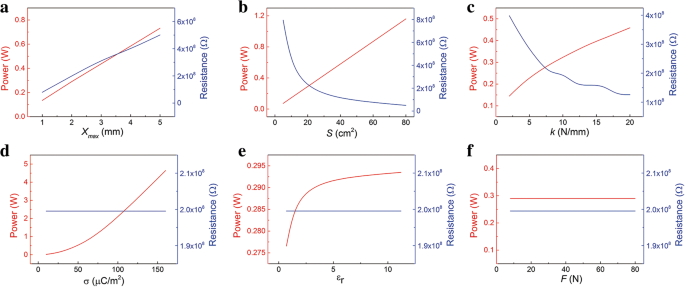
Influencia de los parámetros en la P _máx y la resistencia correspondiente en un ciclo. La relación de P _máx y la resistencia correspondiente con los parámetros a x _máx , b S , c k , d σ, e ε _r y f F

En una palabra, la P _máx se puede aumentar aumentando la distancia de separación máxima x _máx , área S , coeficiente de resorte k , permitividad relativa de la capa dieléctrica ε _r , y especialmente la densidad de carga superficial σ. Por ejemplo, parámetros de material como ε _r y σ generalmente se optimizan para obtener una mayor potencia [28, 29]. Mientras que la resistencia óptima se puede ajustar con los parámetros x _máx , S y k . La P _máx y la resistencia óptima dependen principalmente del material y los parámetros estructurales.

Eficiencia de conversión η de TENG

A veces nos preocupa más P _máx que ignoramos el η . La eficiencia es un parámetro importante para evaluar una fuente de energía. η se define como la relación entre la energía eléctrica de salida y la energía mecánica de entrada. Aquí, hemos investigado de manera sistemática y directa la influencia de estos parámetros en la eficiencia.

La energía eléctrica y la energía mecánica se obtienen de acuerdo con el pulso de corriente en un R óptimo. . La energía eléctrica de salida viene dada por

$$ {E} _ {\ mathrm {eléctrico}} ={\ int} _ {t _ {\ mathrm {inicio}}} ^ {t _ {\ mathrm {end}}} {I} ^ 2 Rdt $$ (13 )

donde el intervalo de tiempo entre t _iniciar y t _final expresa todo un proceso de contacto y separación.

La energía mecánica calculada es

$$ {E} _ {\ mathrm {mecánico}} =F \ veces S $$ (14)

Así, el η se calcula de la siguiente manera

$$ \ eta =\ frac {E _ {\ mathrm {eléctrico}}} {E _ {\ mathrm {mecánico}}} \ veces 100 \% $$ (15)

La relación de η con x _máx se muestra en la Fig. 6a. Como x _máx aumenta, la eficiencia η aumenta y luego se satura gradualmente. Sabemos que la energía mecánica y la potencia máxima es proporcional a x _máx . Sin embargo, aumentar x _máx cambiará el agudo de la curva de tiempo actual. Significa que la tasa de crecimiento se ralentizará cuando x _máx es más grande. La influencia de los parámetros S , k y σ en η se muestran en la Fig. 6b – d. La tendencia creciente de la eficiencia η con estos parámetros es similar al de la potencia máxima. La eficiencia η aumenta gradualmente con la S y k creciente. Sorprendentemente, σ puede influir en gran medida en la eficiencia η . El parámetro ε _r es difícil de cambiar y, afortunadamente, casi no afecta a η como se muestra en la Fig. 6e. Como se muestra en la Fig. 6f, la eficiencia η disminuye rápidamente como F aumenta. Esto se debe principalmente al aumento de la energía mecánica. Obviamente, la eficiencia es relativamente baja. Afortunadamente, podemos aumentar considerablemente la eficiencia mejorando σ.

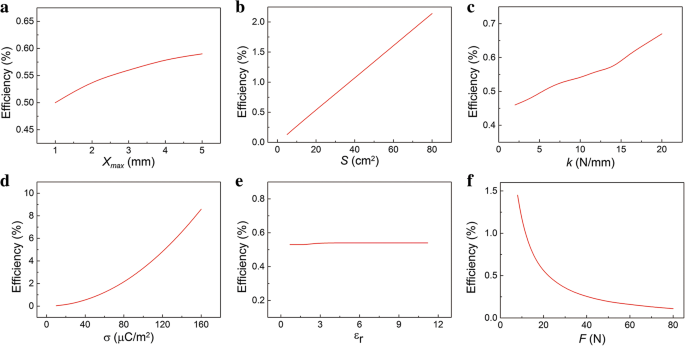
Eficiencia de conversión η de TENG. La relación de la eficiencia de conversión calculada con los parámetros a x _máx , b S , c k , d σ, e ε _r y f F

En la práctica, sin embargo, el F puede afectar al parámetro σ [30]. Bajo la pequeña F , las dos capas son de contacto parcial. Las dos capas pueden tener un mejor contacto como F aumenta. Luego, el parámetro F casi puede afectar la densidad de carga superficial σ. Es decir, σ aumenta con F luego se satura, como se muestra en la Fig. 7a. Por lo tanto, recalculamos la relación entre el rendimiento de salida y la fuerza de compresión F . La influencia de F en la corriente máxima, el voltaje y la potencia instantánea se muestran en la figura 7b – d, respectivamente. Tienen una relación similar con F . Por ejemplo, el voltaje de salida aumenta con F aumentando y luego se mantiene constante, lo cual es consistente con los datos del experimento en la literatura [31, 32]. La influencia de F sobre la energía eléctrica se muestra en la Fig. 7e. Cabe señalar que hay un punto de inflexión en la curva. La energía eléctrica de salida aumenta con F aumentando y luego disminuye ligeramente. La ligera caída de la energía eléctrica de salida se debe al proceso de contacto más corto bajo una F más grande . Bajo una pequeña fuerza de compresión, la F es proporcional a σ, lo que resulta en una mayor producción de energía eléctrica. Sin embargo, bajo una gran fuerza de compresión, σ se satura. Las cargas transferidas en el proceso de separación se mantienen constantes mientras disminuyen en el proceso de contacto bajo una fuerza de compresión mayor. Entonces, la energía eléctrica de salida en todo el proceso de separación y contacto cae ligeramente. La relación de η y F se presenta en la Fig. 7f. Curiosamente, el η - F La curva es un pico agudo y el valor máximo apareció en F ≈ 50 N. La entrada E _mecánico es proporcional a F , mientras que E _mecánico es mucho mayor que la salida E _eléctrico . Bajo la pequeña F , la tasa de crecimiento de E _eléctrico es más rápido que E _mecánico debido al rápido aumento de σ. Sin embargo, en grandes F , la disminución de E _eléctrico y aumento de E _mecánico resultar en una menor eficiencia. El punto de inflexión en la relación entre la eficiencia de conversión de energía y la fuerza de compresión es importante en el diseño de una fuente de energía eficaz.

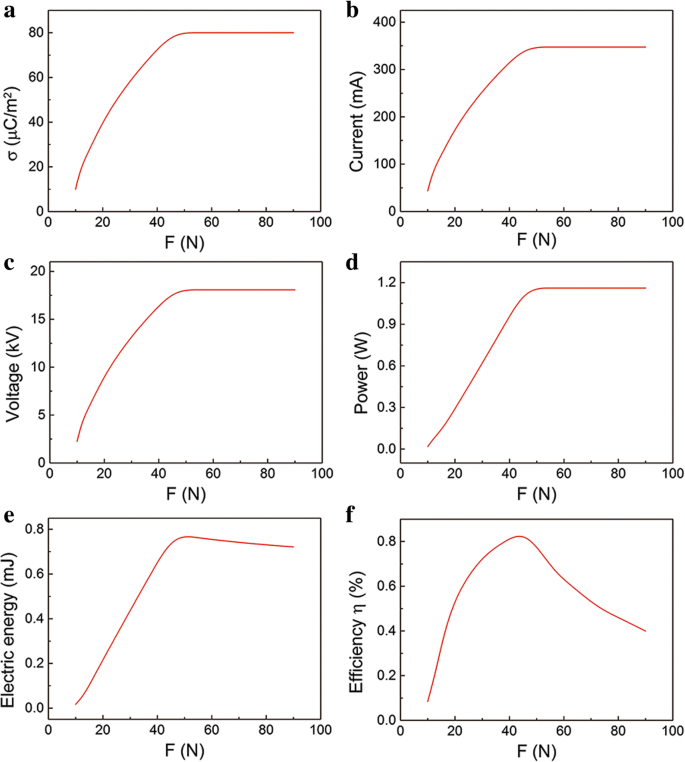
La relación del rendimiento de salida con la fuerza de compresión F en situación práctica. un La influencia de la fuerza de compresión F el a densidad de carga superficial σ, b corriente máxima, c voltaje máximo, d potencia instantánea máxima, e energía eléctrica y f eficiencia

Para obtener un mayor rendimiento de salida, como potencia actual e instantánea, una gran fuerza de compresión F se aplica habitualmente. Pero eso puede causar una baja eficiencia de conversión. De acuerdo con el análisis anterior, podemos elegir una F racional para obtener alta potencia y eficiencia de conversión.

Conclusión

En conclusión, presentamos un enfoque práctico para analizar sistémica y directamente la eficiencia de conversión de los TENG en modo de contacto. Más allá del análisis convencional, se introdujo una fuerza de compresión para obtener un perfil de movimiento más versátil, lo que proporcionó una mejor comprensión del principio operativo del proceso de separación de contactos. Se presentaron las ecuaciones explícitas para el desempeño importante del dispositivo en todo el proceso de separación y contacto, a diferencia del análisis convencional que solo se enfoca en el proceso de separación. En primer lugar, analizamos la relación del rendimiento de salida con el material, la estructura y los parámetros experimentales, que fue principalmente para una mayor potencia de salida. Luego, lo que es más importante, estudiamos de manera sistémica y profunda la influencia de estos parámetros en la eficiencia de conversión de energía en todo el proceso. Es importante destacar que se encontró un punto de inflexión en la relación entre la eficiencia de conversión y la fuerza de compresión. Los TENG con alta potencia de salida y alta eficiencia de conversión se pueden obtener al mismo tiempo con una fuerza óptima. Es realista y útil para TENG más eficientes. Es importante destacar que tiene una buena posibilidad de establecer los estándares para cuantificar la eficiencia de los TENG, lo que sienta las bases para una mayor industrialización y multifuncionalización de los TENG.

Abreviaturas

BE:: Electrodo inferior
TE:: Electrodo superior
TENG:: Nanogeneradores triboeléctricos

Investigación sobre el comportamiento nanomecánico del gradiente del esmalte de fluorosis dental Entrega novedosa de mitoxantrona con nanopartículas de pululano modificadas hidrofóbicamente para inhibir las células cancerosas de la vejiga y el efecto del tamaño de los nanofármacos en la efic…

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias