Tutorial de SciPy en Python:¿Qué es | Biblioteca y ejemplos de funciones
SciPy en Python
SciPy en Python es una biblioteca de código abierto utilizada para resolver problemas matemáticos, científicos, de ingeniería y técnicos. Permite a los usuarios manipular los datos y visualizarlos utilizando una amplia gama de comandos Python de alto nivel. SciPy se basa en la extensión Python NumPy. SciPy también se pronuncia como "Sigh Pi".
Subpaquetes de SciPy:
- Entrada/salida de archivos:scipy.io
- Función especial:scipy.special
- Operación de álgebra lineal:scipy.linalg
- Interpolación:scipy.interpolate
- Optimización y ajuste:scipy.optimize
- Estadísticas y números aleatorios:scipy.stats
- Integración numérica:scipy.integrate
- Transformadas rápidas de Fourier:scipy.fftpack
- Procesamiento de señales:scipy.signal
- Manipulación de imágenes:scipy.ndimage
En este tutorial de Python SciPy, aprenderá:
- ¿Qué es SciPy?
- Por qué usar SciPy
- Numpy VS SciPy
- SciPy:instalación y configuración del entorno
- Paquete de entrada/salida de archivos:
- Paquete de funciones especiales:
- Álgebra lineal con SciPy:
- Transformada discreta de Fourier:scipy.fftpack
- Optimización y ajuste en SciPy:scipy.optimize
- Algoritmo Nelder-Mead:
- Procesamiento de imágenes con SciPy:scipy.ndimage
Por qué usar SciPy
- SciPy contiene variedades de subpaquetes que ayudan a resolver el problema más común relacionado con la computación científica.
- El paquete SciPy en Python es la biblioteca científica más utilizada, solo superada por la biblioteca científica GNU para C/C++ o Matlab.
- Fácil de usar y comprender, así como poder computacional rápido.
- Puede operar en una matriz de la biblioteca NumPy.
Numpy VS SciPy
Numpy:
- Numpy está escrito en C y se usa para cálculos matemáticos o numéricos.
- Es más rápido que otras bibliotecas de Python
- Numpy es la biblioteca más útil para Data Science para realizar cálculos básicos.
- Numpy no contiene nada más que el tipo de datos de matriz que realiza la operación más básica como ordenar, dar forma, indexar, etc.
SciPy:
- SciPy está integrado en la parte superior de NumPy
- El módulo SciPy en Python es una versión completa de álgebra lineal, mientras que Numpy contiene solo algunas funciones.
- La mayoría de las funciones nuevas de Data Science están disponibles en Scipy en lugar de Numpy.
SciPy:instalación y configuración del entorno
También puede instalar SciPy en Windows a través de pip
Python3 -m pip install --user numpy scipy
Instalar Scipy en Linux
sudo apt-get install python-scipy python-numpy
Instalar SciPy en Mac
sudo port install py35-scipy py35-numpy
Antes de comenzar a aprender SciPy Python, debe conocer la funcionalidad básica, así como los diferentes tipos de una matriz de NumPy
La forma estándar de importar módulos SciPy y Numpy:
from scipy import special #same for other modules import numpy as np
Paquete de entrada/salida de archivos:
Scipy, paquete de E/S, tiene una amplia gama de funciones para trabajar con diferentes formatos de archivos que son Matlab, Arff, Wave, Matrix Market, IDL, NetCDF, TXT, CSV y formato binario.
Tomemos un ejemplo de formato de archivo Python SciPy que se usa regularmente en MatLab:
import numpy as np
from scipy import io as sio
array = np.ones((4, 4))
sio.savemat('example.mat', {'ar': array})
data = sio.loadmat(‘example.mat', struct_as_record=True)
data['ar']
Salida:
array([[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.]])
Explicación del código
- Líneas 1 y 2: Importe la biblioteca SciPy esencial en Python con el paquete I/O y Numpy.
- Línea 3 :Crear matriz de 4 x 4, dimensional uno
- Línea 4 :Almacenar matriz en example.mat expediente.
- Línea 5: Obtener datos de example.mat archivo
- Línea 6 :Salida de impresión.
Paquete de funciones especiales
- scipy.especial El paquete contiene numerosas funciones de física matemática.
- La función especial de SciPy incluye raíz cúbica, exponencial, log sum exponencial, Lambert, permutación y combinaciones, gamma, Bessel, hipergeométrica, Kelvin, beta, cilindro parabólico, error relativo exponencial, etc.
- Para una descripción de una línea de todas estas funciones, escriba en la consola de Python:
help(scipy.special)
Output :
NAME
scipy.special
DESCRIPTION
========================================
Special functions (:mod:`scipy.special`)
========================================
.. module:: scipy.special
Nearly all of the functions below are universal functions and follow
broadcasting and automatic array-looping rules. Exceptions are noted.
Función de raíz cúbica:
La función de raíz cúbica encuentra la raíz cúbica de los valores.
Sintaxis:
scipy.special.cbrt(x)
Ejemplo:
from scipy.special import cbrt #Find cubic root of 27 & 64 using cbrt() function cb = cbrt([27, 64]) #print value of cb print(cb)
Salida: matriz([3., 4.])
Función exponencial:
La función exponencial calcula el elemento 10**x.
Ejemplo:
from scipy.special import exp10 #define exp10 function and pass value in its exp = exp10([1,10]) print(exp)
Salida:[1.e+01 1.e+10]
Permutaciones y combinaciones:
SciPy también brinda funcionalidad para calcular permutaciones y combinaciones.
Combinaciones – scipy.especial.peine(N,k)
Ejemplo:
from scipy.special import comb #find combinations of 5, 2 values using comb(N, k) com = comb(5, 2, exact = False, repetition=True) print(com)
Salida:15,0
Permutaciones –
scipy.special.perm(N,k)
Ejemplo:
from scipy.special import perm #find permutation of 5, 2 using perm (N, k) function per = perm(5, 2, exact = True) print(per)
Salida:20
Función exponencial de suma logarítmica
Log Sum Exponential calcula el logaritmo del elemento de entrada exponencial de suma.
Sintaxis :
scipy.special.logsumexp(x)
Función de Bessel
Función de cálculo de orden de número entero N
Sintaxis :
scipy.special.jn()
Álgebra lineal con SciPy
- El álgebra lineal de SciPy es una implementación de las bibliotecas BLAS y ATLAS LAPACK.
- El rendimiento de Álgebra lineal es muy rápido en comparación con BLAS y LAPACK.
- La rutina de álgebra lineal acepta un objeto de matriz bidimensional y la salida también es una matriz bidimensional.
Ahora hagamos una prueba con scipy.linalg,
Cálculo de determinante de una matriz bidimensional,
from scipy import linalg import numpy as np #define square matrix two_d_array = np.array([ [4,5], [3,2] ]) #pass values to det() function linalg.det( two_d_array )
Salida: -7.0
Matriz inversa –
scipy.linalg.inv()
Inverse Matrix of Scipy calcula el inverso de cualquier matriz cuadrada.
A ver,
from scipy import linalg import numpy as np # define square matrix two_d_array = np.array([ [4,5], [3,2] ]) #pass value to function inv() linalg.inv( two_d_array )
Salida:
array( [[-0.28571429, 0.71428571],
[ 0.42857143, -0.57142857]] )
Valores propios y vector propio
scipy.linalg.eig()
- El problema más común en álgebra lineal son los valores propios y los vectores propios, que se pueden resolver fácilmente usando eig()
- Ahora encontremos el valor propio de (X ) y corresponden al vector propio de una matriz cuadrada bidimensional.
Ejemplo
from scipy import linalg import numpy as np #define two dimensional array arr = np.array([[5,4],[6,3]]) #pass value into function eg_val, eg_vect = linalg.eig(arr) #get eigenvalues print(eg_val) #get eigenvectors print(eg_vect)
Salida:
[ 9.+0.j -1.+0.j] #eigenvalues [ [ 0.70710678 -0.5547002 ] #eigenvectors [ 0.70710678 0.83205029] ]
Transformada discreta de Fourier:scipy.fftpack
- DFT es una técnica matemática que se utiliza para convertir datos espaciales en datos de frecuencia.
- FFT (Fast Fourier Transformation) es un algoritmo para calcular DFT
- FFT se aplica a una matriz multidimensional.
- La frecuencia define el número de señales o longitudes de onda en un período de tiempo particular.
Ejemplo: Tome una ola y muestre usando la biblioteca Matplotlib. tomamos el ejemplo de función periódica simple de sin(20 × 2πt)
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
#Frequency in terms of Hertz
fre = 5
#Sample rate
fre_samp = 50
t = np.linspace(0, 2, 2 * fre_samp, endpoint = False )
a = np.sin(fre * 2 * np.pi * t)
figure, axis = plt.subplots()
axis.plot(t, a)
axis.set_xlabel ('Time (s)')
axis.set_ylabel ('Signal amplitude')
plt.show()
Salida:
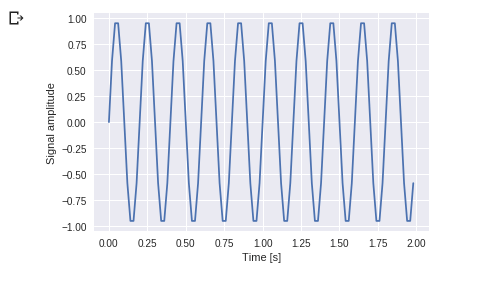
Puedes ver esto. La frecuencia es de 5 Hz y su señal se repite en 1/5 de segundo:se llama como un período de tiempo particular.
Ahora usemos esta onda sinusoidal con la ayuda de la aplicación DFT.
from scipy import fftpack
A = fftpack.fft(a)
frequency = fftpack.fftfreq(len(a)) * fre_samp
figure, axis = plt.subplots()
axis.stem(frequency, np.abs(A))
axis.set_xlabel('Frequency in Hz')
axis.set_ylabel('Frequency Spectrum Magnitude')
axis.set_xlim(-fre_samp / 2, fre_samp/ 2)
axis.set_ylim(-5, 110)
plt.show()
Salida:
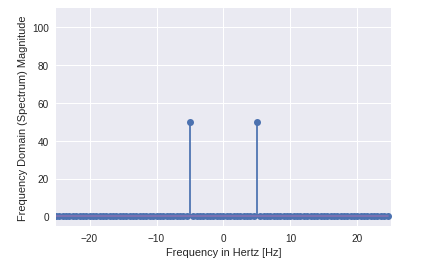
- Puede ver claramente que la salida es una matriz unidimensional.
- La entrada que contiene valores complejos es cero excepto dos puntos.
- En el ejemplo de DFT visualizamos la magnitud de la señal.
Optimización y ajuste en SciPy:scipy.optimize
- Optimization proporciona un algoritmo útil para minimizar el ajuste de curvas, el ajuste multidimensional o escalar y raíz.
- Tomemos un ejemplo de una función escalar, para encontrar la función escalar mínima.
%matplotlib inline
import matplotlib.pyplot as plt
from scipy import optimize
import numpy as np
def function(a):
return a*2 + 20 * np.sin(a)
plt.plot(a, function(a))
plt.show()
#use BFGS algorithm for optimization
optimize.fmin_bfgs(function, 0)
Salida:
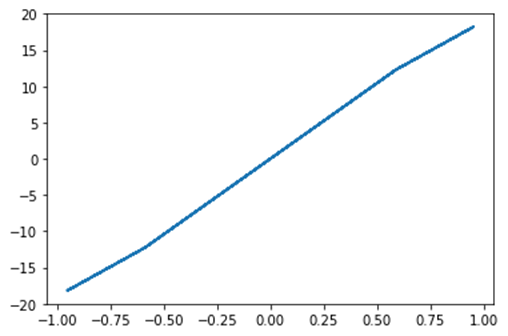
La optimización terminó con éxito.
Valor de la función actual:-23.241676
Iteraciones:4
Evaluaciones de funciones:18
Evaluaciones de gradiente:6
matriz([-1.67096375])
- En este ejemplo, la optimización se realiza con la ayuda del algoritmo de descenso de gradiente desde el punto inicial
- Pero el posible problema son los mínimos locales en lugar de los mínimos globales. Si no encontramos un vecino de los mínimos globales, entonces debemos aplicar la optimización global y encontrar la función de mínimos globales utilizada como basinhopping() que combina optimizador local.
optimize.basinhopping(función, 0)
Salida:
fun: -23.241676238045315
lowest_optimization_result:
fun: -23.241676238045315
hess_inv: array([[0.05023331]])
jac: array([4.76837158e-07])
message: 'Optimization terminated successfully.'
nfev: 15
nit: 3
njev: 5
status: 0
success: True
x: array([-1.67096375])
message: ['requested number of basinhopping iterations completed successfully']
minimization_failures: 0
nfev: 1530
nit: 100
njev: 510
x: array([-1.67096375])
Algoritmo Nelder-Mead:
- El algoritmo de Nelder-Mead selecciona a través del parámetro del método.
- Proporciona la forma más directa de minimización para una función de comportamiento justo.
- Nelder:el algoritmo Mead no se utiliza para las evaluaciones de gradiente porque puede llevar más tiempo encontrar la solución.
import numpy as np
from scipy.optimize import minimize
#define function f(x)
def f(x):
return .4*(1 - x[0])**2
optimize.minimize(f, [2, -1], method="Nelder-Mead")
Salida:
final_simplex: (array([[ 1. , -1.27109375],
[ 1. , -1.27118835],
[ 1. , -1.27113762]]), array([0., 0., 0.]))
fun: 0.0
message: 'Optimization terminated successfully.'
nfev: 147
nit: 69
status: 0
success: True
x: array([ 1. , -1.27109375])
Procesamiento de imágenes con SciPy:scipy.ndimage
- scipy.ndimage es un submódulo de SciPy que se usa principalmente para realizar una operación relacionada con imágenes
- ndimage significa la imagen dimensional "n".
- El procesamiento de imágenes de SciPy proporciona transformación geométrica (rotar, recortar, voltear), filtrado de imágenes (nítidas y delineadas), visualización de imágenes, segmentación de imágenes, clasificación y extracción de características.
- Paquete MISC en SciPy contiene imágenes prediseñadas que se pueden usar para realizar tareas de manipulación de imágenes
Ejemplo: Tomemos un ejemplo de transformación geométrica de imágenes
from scipy import misc from matplotlib import pyplot as plt import numpy as np #get face image of panda from misc package panda = misc.face() #plot or show image of face plt.imshow( panda ) plt.show()
Salida:
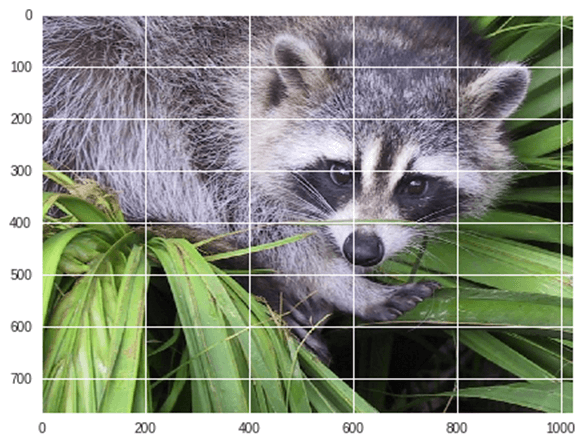
Ahora Volteamos hacia abajo imagen actual:
#Flip Down using scipy misc.face image flip_down = np.flipud(misc.face()) plt.imshow(flip_down) plt.show()
Salida:
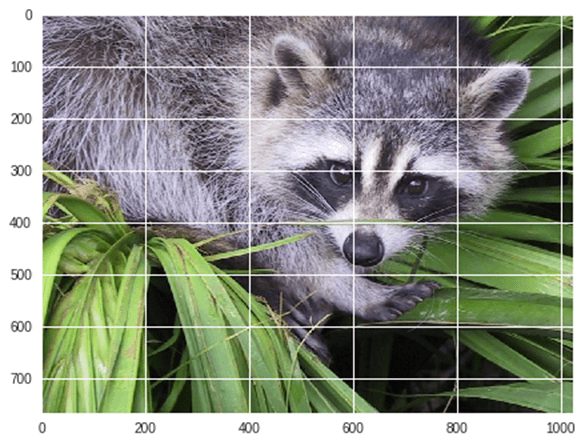
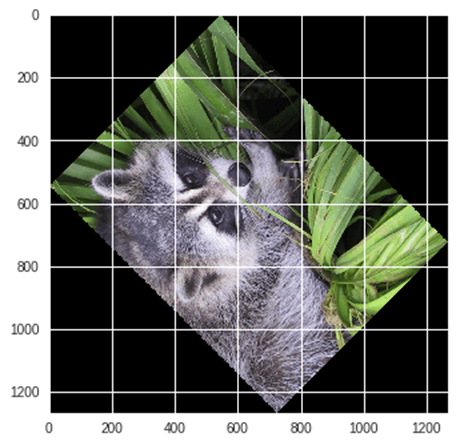
Ejemplo: Rotación de imagen usando Scipy,
from scipy import ndimage, misc from matplotlib import pyplot as plt panda = misc.face() #rotatation function of scipy for image – image rotated 135 degree panda_rotate = ndimage.rotate(panda, 135) plt.imshow(panda_rotate) plt.show()
Salida:
Integración con Scipy – Integración Numérica
- Cuando integramos cualquier función donde la integración analítica no es posible, debemos recurrir a la integración numérica
- SciPy proporciona funcionalidad para integrar funciones con integración numérica.
- scipy.integrate La biblioteca tiene integración simple, doble, triple, múltiple, cuadrado gaussiano, reglas de Romberg, trapezoidal y de Simpson.
Ejemplo: Ahora tome un ejemplo de Integración única
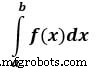
Aquí un es el límite superior y b es el límite inferior
from scipy import integrate # take f(x) function as f f = lambda x : x**2 #single integration with a = 0 & b = 1 integration = integrate.quad(f, 0 , 1) print(integration)
Salida:
(0.33333333333333337, 3.700743415417189e-15)
Aquí la función devuelve dos valores, en los que el primer valor es la integración y el segundo valor es el error estimado en la integral.
Ejemplo:Ahora tome un ejemplo de SciPy de integración doble. Encontramos la doble integración de la siguiente ecuación,
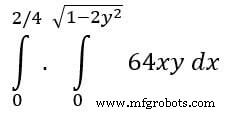
from scipy import integrate import numpy as np #import square root function from math lib from math import sqrt # set fuction f(x) f = lambda x, y : 64 *x*y # lower limit of second integral p = lambda x : 0 # upper limit of first integral q = lambda y : sqrt(1 - 2*y**2) # perform double integration integration = integrate.dblquad(f , 0 , 2/4, p, q) print(integration)
Salida:
(3.0, 9.657432734515774e-14)
Ha visto el resultado anterior como el mismo anterior.
Resumen
- SciPy (pronunciado como "Sigh Pi") es una biblioteca de código abierto basada en Python, que se utiliza en matemáticas, computación científica, ingeniería y computación técnica.
- SciPy contiene variedades de subpaquetes que ayudan a resolver el problema más común relacionado con la computación científica.
- SciPy está integrado en la parte superior de NumPy
| Nombre del paquete | Descripción |
|---|---|
| scipy.io |
|
| scipy.especial |
|
| scipy.linalg |
|
| scipy.interpolar |
|
| scipy.optimizar |
|
| scipy.stats |
|
| scipy.integrar |
|
| scipy.fftpack |
|
| scipy.signal |
|
| scipy.ndimage |
|
python
- Declaración Python Print():cómo imprimir con ejemplos
- Python String count () con EJEMPLOS
- Python String format() Explicar con EJEMPLOS
- Método Python String find() con ejemplos
- Funciones Python Lambda con EJEMPLOS
- Función Python abs():Ejemplos de valores absolutos
- Función Python round() con EJEMPLOS
- Función Python map() con EJEMPLOS
- Python Timeit() con ejemplos
- Tutorial de Rendimiento en Python:Generador y Rendimiento vs Ejemplo de Retorno
- type() y isinstance() en Python con ejemplos



