Introducción a los números complejos

Si tuviera que describir la distancia entre dos ciudades, podría dar una respuesta que consista en un solo número en millas, kilómetros o alguna otra unidad de medida lineal.

Sin embargo, si tuviera que describir cómo viajar de una ciudad a otra, tendría que proporcionar más información que solo la distancia entre esas dos ciudades; También tendría que proporcionar información sobre la dirección viajar, también.

El tipo de información que expresa una sola dimensión, como la distancia lineal, se denomina escalar cantidad en matemáticas. Los números escalares son el tipo de números que ha utilizado en la mayoría de sus aplicaciones matemáticas hasta ahora.

El voltaje producido por una batería, por ejemplo, es una cantidad escalar. También lo es la resistencia de un trozo de cable (ohmios) o la corriente que lo atraviesa (amperios).

Sin embargo, cuando comenzamos a analizar circuitos de CA, encontramos esa cantidad de voltaje, corriente e incluso resistencia (llamada impedancia en CA) no son las conocidas cantidades unidimensionales que estamos acostumbrados a medir en circuitos de CC.

Más bien, estas cantidades, por ser dinámicas (alternas en dirección y amplitud), poseen otras dimensiones que deben tenerse en cuenta. La frecuencia y el cambio de fase son dos de estas dimensiones que entran en juego.

Incluso con circuitos de CA relativamente simples, donde solo estamos tratando con una sola frecuencia, todavía tenemos que lidiar con la dimensión del cambio de fase además de la amplitud.

Para analizar con éxito los circuitos de CA, necesitamos trabajar con objetos y técnicas matemáticas capaces de representar estas cantidades multidimensionales.

Aquí es donde debemos abandonar los números escalares por algo más adecuado: números complejos . Al igual que en el ejemplo de dar direcciones de una ciudad a otra, las cantidades de CA en un circuito de frecuencia única tienen tanto amplitud (analogía:distancia) como desplazamiento de fase (analogía:dirección).

Un número complejo es una única cantidad matemática capaz de expresar estas dos dimensiones de amplitud y cambio de fase a la vez.

Representación gráfica de números complejos

Los números complejos son más fáciles de comprender cuando se representan gráficamente. Si dibujo una línea con una cierta longitud (magnitud) y ángulo (dirección), tengo una representación gráfica de un número complejo que se conoce comúnmente en física como un vector :(Figura siguiente)

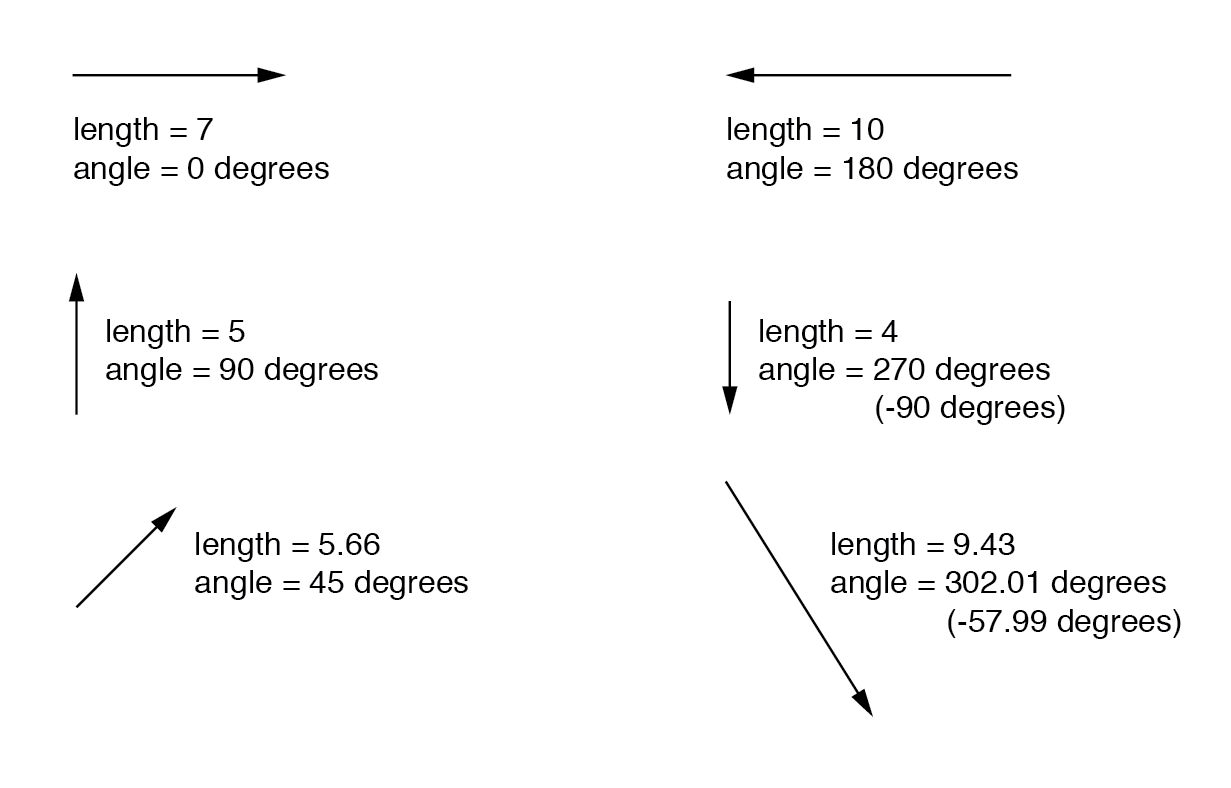
Como distancias y direcciones en un mapa, debe haber un marco de referencia común para que las figuras de ángulos tengan algún significado. En este caso, directamente a la derecha se considera 0 ^o , y los ángulos se cuentan en una dirección positiva en sentido antihorario:(Figura siguiente)

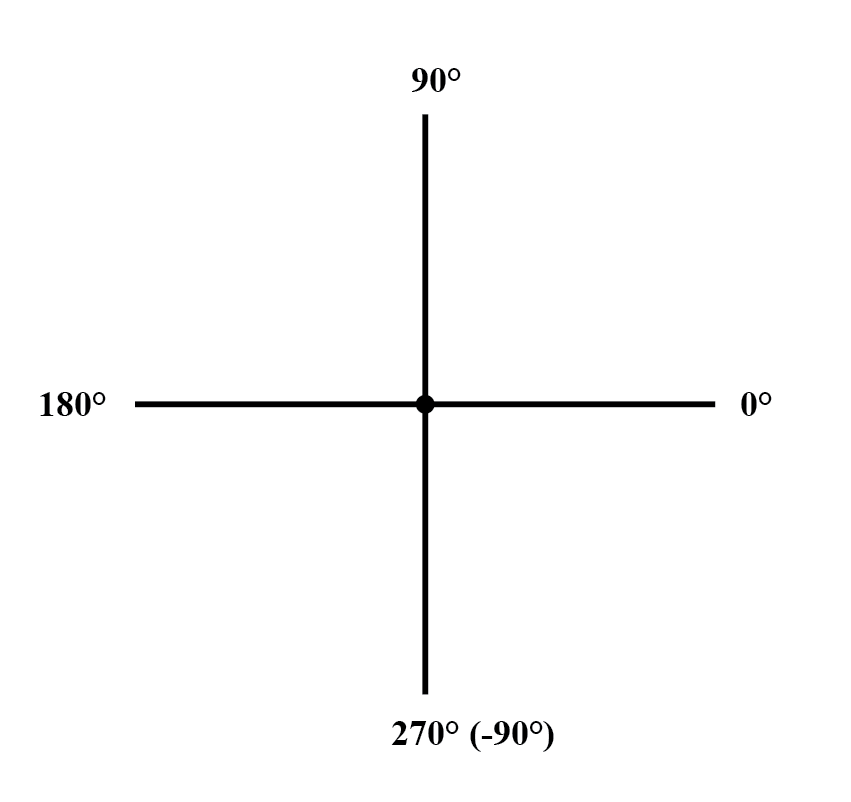
La idea de representar un número en forma gráfica no es nada nuevo. Todos aprendimos esto en la escuela primaria con la "recta numérica:" (Figura siguiente)

Incluso aprendimos cómo funcionan la suma y la resta al ver cómo se apilan las longitudes (magnitudes) para dar una respuesta final:(Figura siguiente)

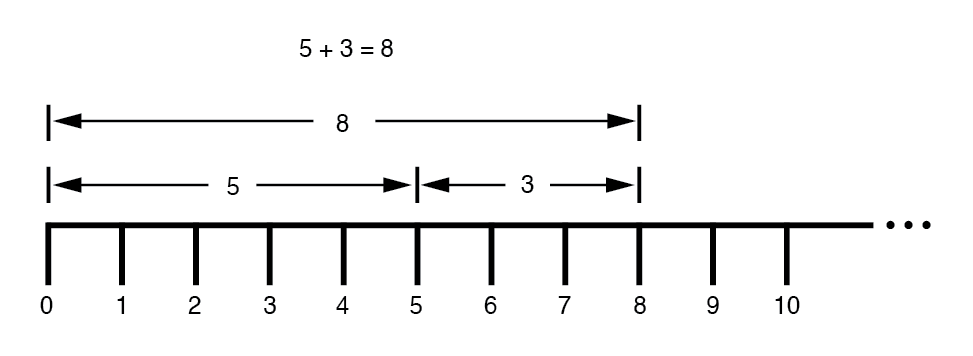
Más tarde, supimos que había formas de designar los valores entre los números enteros marcados en la línea. Se trataba de cantidades fraccionarias o decimales:(Imagen siguiente)

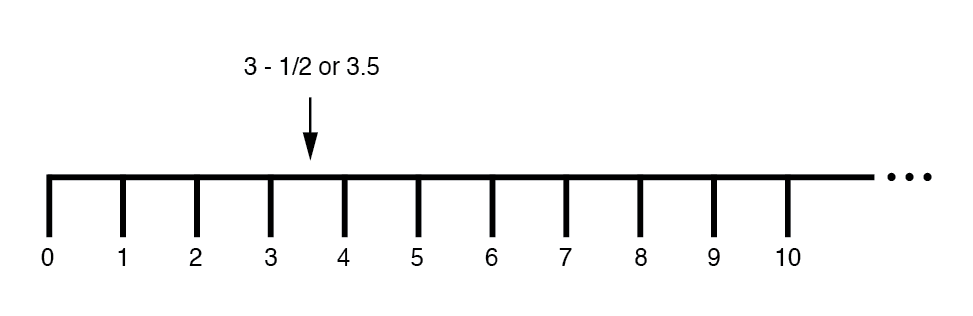
Estos campos de números (enteros, enteros, racionales, irracionales, reales, etc.) que se aprenden en la escuela primaria comparten un rasgo común:todos son unidimensionales . La rectitud de la recta numérica ilustra esto gráficamente.

Puede moverse hacia arriba o hacia abajo en la línea numérica, pero todo el "movimiento" a lo largo de esa línea está restringido a un solo eje (horizontal).

Los números escalares unidimensionales son perfectamente adecuados para contar cuentas, representar el peso o medir el voltaje de la batería de CC, pero no pueden representar algo más complejo como la distancia y dirección entre dos ciudades, o la amplitud y fase de una forma de onda de CA.

Para representar este tipo de cantidades, necesitamos representaciones multidimensionales. En otras palabras, necesitamos una recta numérica que pueda apuntar en diferentes direcciones, y eso es exactamente lo que es un vector.

REVISAR:

• Un escalar número es el tipo de objeto matemático que las personas están acostumbradas a usar en la vida cotidiana:una cantidad unidimensional como temperatura, longitud, peso, etc.
• Un número complejo es una cantidad matemática que representa dos dimensiones de magnitud y dirección.
• Un vector es una representación gráfica de un número complejo. Parece una flecha, con un punto de partida, una punta, una longitud definida y una dirección definida. A veces, la palabra fasor se utiliza en aplicaciones eléctricas donde el ángulo del vector representa el cambio de fase entre formas de onda.

HOJA DE TRABAJO RELACIONADA:

• Hoja de trabajo de la fase de CA