Cableado del circuito

Hasta ahora, hemos estado analizando circuitos de una sola batería y una sola resistencia sin tener en cuenta los cables de conexión entre los componentes, siempre que se forme un circuito completo. ¿Importa la longitud del cable o la “forma” del circuito para nuestros cálculos? Veamos un par de diagramas de circuitos y descubramos:

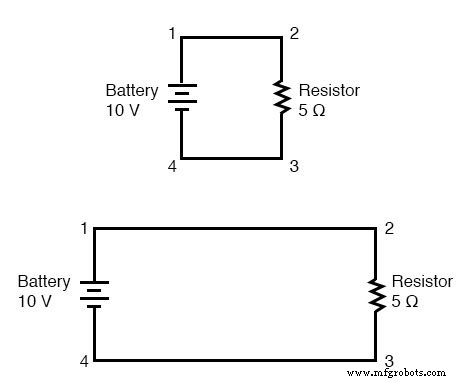
Cuando dibujamos cables que conectan puntos en un circuito eléctrico, generalmente asumimos que esos cables tienen una resistencia insignificante. Como tales, no contribuyen de manera apreciable a la resistencia general del circuito, por lo que la única resistencia con la que tenemos que lidiar es la resistencia en los componentes. En los circuitos anteriores, la única resistencia proviene de las resistencias de 5 Ω, por lo que es todo lo que consideraremos en nuestros cálculos.

En la vida real, los cables metálicos sí tienen resistencia (¡y también las fuentes de energía!), pero esas resistencias son generalmente mucho más pequeñas que la resistencia presente en los otros componentes del circuito que pueden ignorarse con seguridad. Existen excepciones a esta regla en el cableado del sistema de energía, donde incluso cantidades muy pequeñas de resistencia del conductor pueden crear caídas de voltaje significativas dados los niveles normales (altos) de corriente.

Puntos eléctricamente comunes en un circuito

Si la resistencia del cable de conexión es muy pequeña o nula, podemos considerar que los puntos conectados en un circuito son eléctricamente comunes . Es decir, los puntos 1 y 2 de los circuitos anteriores pueden estar físicamente unidos juntos o muy separados, y no importa para ninguna medición de voltaje o resistencia relativa a esos puntos.

Lo mismo ocurre con los puntos 3 y 4. Es como si los extremos de la resistencia estuvieran conectados directamente a los terminales de la batería, en lo que respecta a los cálculos de la ley de Ohm y las mediciones de voltaje.

Es útil saberlo, porque significa que puede volver a dibujar un diagrama de circuito o volver a cablear un circuito, acortando o alargando los cables como desee sin afectar apreciablemente la función del circuito. Todo lo que importa es que los componentes se unan entre sí en la misma secuencia.

También significa que las mediciones de voltaje entre conjuntos de puntos "eléctricamente comunes" serán las mismas. Es decir, el voltaje entre los puntos 1 y 4 (directamente a través de la batería) será el mismo que el voltaje entre los puntos 2 y 3 (directamente a través de la resistencia). Observe de cerca el siguiente circuito e intente determinar qué puntos son comunes entre sí:

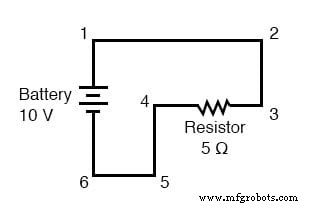
Aquí, solo tenemos 2 componentes excluyendo los cables:la batería y la resistencia. Aunque los cables de conexión toman un camino complicado para formar un circuito completo, hay varios puntos eléctricamente comunes en el camino de la corriente. Los puntos 1, 2 y 3 son todos comunes entre sí, porque están conectados directamente entre sí por cable. Lo mismo ocurre con los puntos 4, 5 y 6.

El voltaje entre los puntos 1 y 6 es de 10 voltios y proviene directamente de la batería. Sin embargo, dado que los puntos 5 y 4 son comunes a 6, y los puntos 2 y 3 comunes a 1, esos mismos 10 voltios también existen entre estos otros pares de puntos:

 Entre los puntos 1 y 4 =10 voltios Entre los puntos 2 y 4 =10 voltios Entre los puntos 3 y 4 =10 voltios (directamente a través de la resistencia) Entre los puntos 1 y 5 =10 voltios Entre los puntos 2 y 5 =10 voltios Entre los puntos 3 y 5 =10 voltios Entre los puntos 1 y 6 =10 voltios (directamente a través de la batería) Entre los puntos 2 y 6 =10 voltios Entre los puntos 3 y 6 =10 voltios 

Dado que los puntos eléctricamente comunes están conectados entre sí mediante un cable (resistencia cero), no hay una caída de voltaje significativa entre ellos, independientemente de la cantidad de corriente conducida de uno a otro a través de ese cable de conexión. Por lo tanto, si tuviéramos que leer voltajes entre puntos comunes, deberíamos mostrar (prácticamente) cero:

 Entre los puntos 1 y 2 =0 voltios Los puntos 1, 2 y 3 están entre los puntos 2 y 3 =0 voltios eléctricamente comunes Entre los puntos 1 y 3 =0 voltios Entre los puntos 4 y 5 =0 voltios Los puntos 4, 5 y 6 están entre los puntos 5 y 6 =0 voltios eléctricamente comunes Entre los puntos 4 y 6 =0 voltios 

Cálculo de la caída de voltaje con la ley de Ohm

Esto también tiene sentido matemáticamente. Con una batería de 10 voltios y una resistencia de 5 Ω, la corriente del circuito será de 2 amperios. Si la resistencia del cable es cero, la caída de voltaje en cualquier tramo continuo de cable se puede determinar mediante la Ley de Ohm como tal:

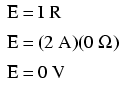
Debería ser obvio que la caída de voltaje calculada a través de cualquier longitud ininterrumpida de cable en un circuito donde se supone que el cable tiene resistencia cero siempre será cero, sin importar la magnitud de la corriente, ya que cero multiplicado por cualquier cosa es igual a cero.

Debido a que los puntos comunes en un circuito exhibirán las mismas medidas relativas de voltaje y resistencia, los cables que conectan puntos comunes a menudo se etiquetan con la misma designación. Esto no quiere decir que la terminal los puntos de conexión están etiquetados de la misma manera, solo los cables de conexión. Tome este circuito como ejemplo:

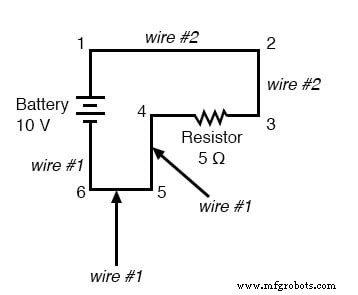
Los puntos 1, 2 y 3 son todos comunes entre sí, por lo que el punto de conexión de cables 1 a 2 tiene la misma etiqueta (cable 2) que el punto de conexión de cables 2 a 3 (cable 2). En un circuito real, el cable que se extiende desde el punto 1 al 2 puede que ni siquiera sea del mismo color o tamaño que el cable que conecta el punto 2 a 3, pero deben llevar exactamente la misma etiqueta. Lo mismo ocurre con los cables que conectan los puntos 6, 5 y 4.

La caída de voltaje debe ser igual a cero en puntos comunes

Saber que los puntos eléctricamente comunes tienen una caída de voltaje cero entre ellos es un principio valioso para la resolución de problemas. Si mido el voltaje entre puntos en un circuito que se supone que son comunes entre sí, debería leer cero.

Sin embargo, si leo un voltaje sustancial entre esos dos puntos, entonces sé con certeza que no pueden conectarse directamente entre sí. Si esos puntos son supuestos para ser eléctricamente común pero registran lo contrario, entonces sé que hay una "falla abierta" entre esos puntos.

Voltaje cero significa técnicamente un voltaje insignificante

Una nota final:para la mayoría de los propósitos prácticos, se puede suponer que los conductores de alambre poseen resistencia cero de un extremo a otro. En realidad, sin embargo, siempre se encontrará una pequeña cantidad de resistencia a lo largo de la longitud de un cable, a menos que sea un cable superconductor. Sabiendo esto, debemos tener en cuenta que los principios aprendidos aquí sobre los puntos comunes eléctricamente son todos válidos en gran medida, pero no en un absoluto grado.

Es decir, la regla de que se garantiza que los puntos eléctricamente comunes tienen voltaje cero entre ellos se establece con mayor precisión como tal:los puntos eléctricamente comunes tendrán muy poco el voltaje cayó entre ellos. Ese pequeño, prácticamente inevitable rastro de resistencia que se encuentra en cualquier trozo de cable de conexión está destinado a crear un pequeño voltaje a lo largo del mismo a medida que se conduce la corriente.

Siempre que comprenda que estas reglas se basan en ideal condiciones, no se quedará perplejo cuando se encuentre con alguna condición que parezca ser una excepción a la regla.

REVISAR:

• Se supone que los cables de conexión en un circuito tienen resistencia cero a menos que se indique lo contrario.
• Los cables de un circuito se pueden acortar o alargar sin afectar la función del circuito; todo lo que importa es que los componentes estén conectados entre sí en la misma secuencia.
• Los puntos conectados directamente entre sí en un circuito por resistencia cero (cable) se consideran eléctricamente comunes .
• Los puntos eléctricamente comunes, con resistencia cero entre ellos, tendrán una caída de voltaje cero entre ellos, independientemente de la magnitud de la corriente (idealmente).
• Las lecturas de voltaje o resistencia a las que se hace referencia entre conjuntos de puntos eléctricamente comunes serán las mismas.
• Estas reglas se aplican a ideal condiciones, donde se supone que los cables de conexión poseen una resistencia absolutamente nula. En la vida real, probablemente este no será el caso, pero las resistencias de los cables deben ser lo suficientemente bajas para que los principios generales establecidos aquí se mantengan.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de circuitos simples
• Hoja de trabajo del circuito elemental
• Hoja de trabajo del circuito divisor de voltaje