home Tecnología de fabricación Equipo de fabricación
Manufactura industrial
Internet industrial de las cosas | Materiales industriales | Mantenimiento y reparación de equipos | Programación industrial |
home  MfgRobots >> Manufactura industrial >  >> Industrial materials >> Nanomateriales

Estructura electrónica y características I-V de las nanocintas InSe

Resumen

Hemos estudiado la estructura electrónica y la corriente-voltaje ( I-V ) características de las nanocintas InSe unidimensionales utilizando la teoría de la función de densidad combinada con el método de función de Green sin equilibrio. Se tienen en cuenta las nanocintas que tienen bordes desnudos o pasivados en H de tipo zigzag (Z), Klein (K) y sillón (A). Se encuentra que los estados de borde juegan un papel importante en la determinación de sus propiedades electrónicas. Los bordes Z y K suelen ser metálicos en nanocintas anchas, así como sus contrapartes hidrogenadas. La transición de semiconductor a metal se observa en nanocintas hidrogenadas HZZH a medida que aumenta su ancho, debido a la fuerte dependencia del ancho de la diferencia de energía entre los estados del borde izquierdo y derecho. Sin embargo, las estructuras electrónicas de otras nanocintas varían con el ancho en una escala muy limitada. El I-V Las características de las nanocintas desnudas ZZ y KK muestran una fuerte resistencia diferencial negativa, debido al desajuste espacial de las funciones de onda en las bandas de energía alrededor de la energía de Fermi. También se predice la polarización de espín en estas nanocintas. Por el contrario, las nanocintas AA desnudas y sus homólogos hidrogenados HAAH son semiconductores. Las brechas de banda de las nanocintas AA (HAAH) son más estrechas (más anchas) que las de la monocapa bidimensional de InSe y aumentan (disminuyen) con el ancho de las nanocintas.

Antecedentes

Los materiales bidimensionales (2D) atómicamente delgados han atraído un gran interés en la última década debido a sus propiedades electrónicas únicas y su potencial de aplicación prometedor [1, 2, 3, 4] originado principalmente por su dimensionalidad reducida. Las nanocintas unidimensionales (1D) se pueden fabricar adaptando los materiales 2D [5] o ensamblando átomos con precisión de abajo hacia arriba [6, 7]. En las nanocintas, las propiedades electrónicas se modulan aún más mediante un confinamiento adicional y una posible funcionalización de los bordes [8, 9]. Por ejemplo, su brecha de energía, un parámetro clave del semiconductor, puede ajustarse continuamente por su ancho [10,11,12,13,14,15]. Los enlaces colgantes de los átomos de los bordes pueden ser pasivados por átomos de H en un entorno adecuado, y la hidrogenación puede estabilizar los bordes de la reconstrucción estructural [16, 17].

Recientemente, se ha agregado un nuevo miembro, la monocapa InSe, a los materiales 2D. Bulk InSe pertenece a la familia de semiconductores de calcogenuros metálicos en capas y se ha estudiado intensamente en las últimas décadas [18,19,20,21,22]. Cada una de sus capas cuádruples tiene una red hexagonal que consiste efectivamente en cuatro planos atómicos Se-In-In-Se enlazados covalentemente. Las capas cuádruples se apilan juntas mediante interacciones de van der Waals a una distancia entre capas de aproximadamente 0,8 nm. El estilo de apilamiento define sus politipos como β, γ y ε, entre los cuales los β y γ tienen espacios de banda directos. Sin embargo, la única capa cuádruple de InSe se fabricó con éxito sólo en los últimos años mediante el método de exfoliación mecánica [23, 24]. Desde entonces, la extraordinaria movilidad de electrones elevada y las propiedades físicas especiales de las monocapas de InSe han desencadenado un extenso estudio sobre sus posibles aplicaciones en dispositivos optoelectrónicos [24, 25, 26] y dispositivos electrónicos [27, 28]. En aras de explorar nuevas propiedades funcionales, el estudio teórico también puede ser un enfoque eficiente. Se han realizado simulaciones numéricas de las propiedades estructurales, eléctricas y magnéticas de las monocapas de InSe y su modulación por dopaje, defecto y adsorción [29,30,31,32,33,34,35,36,37,38]. Las estructuras de bandas de InSe de una y pocas capas se han estudiado cuidadosamente mediante la teoría funcional de la densidad [29]. Se han descubierto los defectos intrínsecos dominantes en la monocapa de InSe [30], y se han estimado las propiedades de los defectos nativos y las impurezas de sustitución en la monocapa de InSe mediante el cálculo de las energías de formación e ionización [31]. Además, se ha predicho que el dopaje sustitutivo de átomos de As puede transferir la monocapa de InSe de semiconductor no magnético a semiconductor magnético / metal o semimetal [32]. La conductividad térmica de las monocapas de InSe se puede modular en gran medida por su tamaño [33]. Sin embargo, hasta donde sabemos, existen pocos estudios sobre las propiedades electrónicas de nanocintas unidimensionales de monocapa de InSe hasta ahora.

En este artículo, llevamos a cabo una simulación de los primeros principios sobre las propiedades electrónicas de nanocintas en zigzag desnudo 1D, sillón y monocapa InSe de Klein y sus contrapartes pasivadas con hidrógeno. Nuestros estudios indican la transición de semiconductores a metal en nanocintas en zigzag de InSe pasivadas con hidrógeno y el interesante cambio de brecha de energía en las nanocintas de sillón. Las curvas de corriente-voltaje muestran propiedades eléctricas diversificadas para nanocintas con diferentes bordes.

Métodos

Se tienen en cuenta los tres patrones de borde típicos de celosía de nido de abeja, zigzag (Z), sillón (A) y Klein (K) [39]. Como se ilustra en la Fig.1, una nanocinta puede identificarse por su número de ancho n y la combinación de los tipos de sus dos aristas. Hay cinco clases de nanocintas desnudas: n -ZZ, n -AA, n -KK, n -ZK y n -KZ. Tenga en cuenta que n -ZK es diferente de n -KZ porque suponemos que el borde Z izquierdo (derecho) termina con átomos de In (Se). Si cada átomo de borde está pasivado por un átomo de hidrógeno, denotamos las nanocintas pasivadas como n -HZZH, n -HAAH, n -HKKH, n -HZKH y n -HKZH, respectivamente. Se utiliza una capa cuádruple de Se-In-In-Se de constante de celosía de 4,05 Å con una distancia de capa de Se-In de 0,055 Å y una distancia de capa de In-In de 0,186 Å para fabricar nanocintas antes de la optimización de la geometría [21].

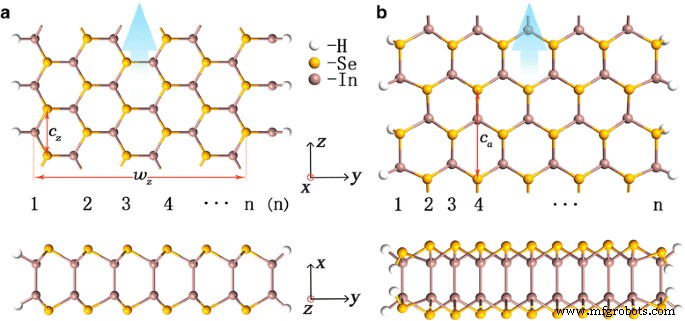
Vistas superior y lateral de 6-HZKH ( a ) y 11-HAAH ( b ) Nanocintas InSe. Número de ancho de nanocintas n , ancho w z y constantes de celosía c z o c a están marcados

Todos los cálculos se realizan utilizando el Atomistix ToolKit (ATK) basado en DFT con la técnica pseudopotencial. Se adopta la correlación de intercambio funcional en la aproximación de densidad de espín local con la parametrización Perdew-Zunger (LSDA-PZ). Las funciones de onda se expanden sobre la base de un conjunto de orbitales de doble ζ más un orbital de polarización (DZP). Un corte de energía de 3000 eV, a k -rejilla de malla espacial de 1 × 1 × 100, y una temperatura electrónica de 300 K se utilizan en la integración del eje real para las funciones de Green en no equilibrio. Se adopta una capa de vacío de 15 Å de espesor en las supercélulas para separar las nanocintas de sus imágenes vecinas tanto en x y y direcciones y asegurar la supresión del acoplamiento entre ellos. Las estructuras de banda se calculan después de la relajación total de la geometría con una tolerancia de fuerza de 0.02 eV / Å −1 .

Para simular la propiedad de transporte electrónico de las nanocintas, conectamos cada una en un circuito con potencial químico izquierdo (derecho) μ L ( μ R ) [40, 41]. La nanocinta se puede dividir en tres regiones, el electrodo izquierdo (derecho) L (R) y la región central C. La corriente dependiente del espín puede estimarse mediante la fórmula de Landauer-Büttiker [42].

$$ {I} _ {\ sigma} \ left ({V} _b \ right) =\ frac {e} {h} {\ int} _ {- \ infty} ^ {+ \ infty} {T} _ { \ sigma} \ left (E, {V} _b \ right) \ left [{f} _L \ left (E - {\ mu} _L \ right) - {f} _R \ left (E - {\ mu} _R \ derecha) \ derecha] dE $$

con giro σ =↑, ↓ y polarización de voltaje V b =( μ R - μ L ) / e . Aquí, \ ({T} _ {\ sigma} \ left (E, {V} _b \ right) =Tr \ left [{\ Gamma} _L {G} _ {\ sigma} {\ Gamma} _R {G} _ {\ sigma} ^ {\ dagger} \ right] \) es el espectro de transmisión con G σ la función de Green retardada en la región C y Γ L (Γ R ) la matriz de acoplamiento entre C y L (R). f L ( f R ) es la función de distribución de Fermi de electrones en L (R).

Resultados y discusión

En la Fig. 1, esquematizamos las vistas superior y lateral de (a) nanocintas 6-HZKH y (b) 11-HAAH con constantes de celosía c z =4.05 Å y c a =7,01 Å, respectivamente. El borde K está a lo largo de la dirección paralela a la del borde Z. La dirección de extensión z de la nanocinta está marcada con flechas azules. A diferencia del caso de las nanocintas de grafeno [39], no se observa reconstrucción de bordes para los tres estilos de bordes en nanocintas InSe desnudas y pasivadas con H, y nuestra simulación indica que todos son energéticamente estables.

Desnudo n Las nanocintas -ZZ son metales magnéticos excepto el 2-ZZ que tiene una geometría reconstruida y parece semiconductor. Tienen estructuras de bandas similares a las ilustradas en la Fig. 2a. La p Los orbitales de los átomos de borde Se dominan la contribución a los estados cercanos a la energía de Fermi, similar al caso de la monocapa de InSe [32], pero aquí se observan más contribuciones de los átomos de In. Las dos bandas parcialmente ocupadas son de los estados del borde izquierdo y derecho, respectivamente, como se muestra en los estados de Bloch de punto Г para la nanocinta 4-ZZ. Uno de ellos es la división de espín y un momento magnético neto, p. Ej., 0,706 μ B para nanocintas 4-ZZ, aparece en cada celda primitiva en el borde izquierdo.

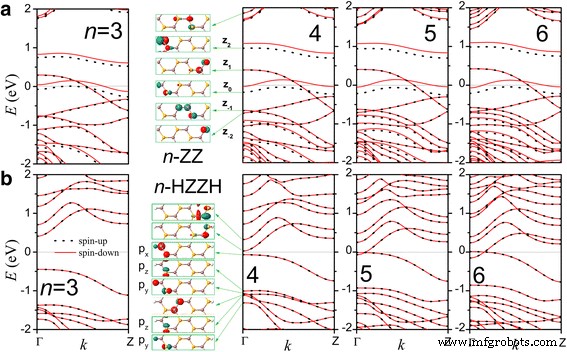
Las estructuras de bandas de a Nanocintas de 3, 4, 5 y 6 ZZ y b Nanocintas de 3, 4, 5 y 6-HZZH. Los estados de Bloch de punto Г cerca de la energía de Fermi se muestran para n =4. Las órbitas de los estados por debajo de la energía de Fermi están indicadas para la nanocinta 4-HZZH

Cuando los átomos del borde son pasivados por átomos de H, n -Las nanocintas HZZH se convierten en semiconductores no magnéticos para n =3, 4 y metal para n > 4 como se muestra en la Fig. 2b. Tenga en cuenta que la estructura se vuelve inestable para n =2. En la nanocinta 4-HZZH, los estados de Bloch en Г en las bandas de conducción (valencia) cerca de la energía de Fermi están confinadas al borde derecho (izquierdo). Tienen componentes similares a los de la monocapa 2D InSe, excepto las partes orbitales atómicas H. Las cinco bandas más altas de los estados del borde izquierdo se componen de una p x , dos p años y dos p z orbitales de átomos de borde de Se. Las bandas de energía de los estados del borde derecho (izquierdo) son similares a las bandas de conducción (valencia) en la dirección Γ-K de la monocapa 2D InSe [32]. Su separación de energía depende en gran medida de n aunque sus dispersiones son insensibles a n . Definimos E d como la diferencia de energía entre el mínimo de los estados del borde derecho y el máximo de los estados del borde izquierdo.

En la figura 3, graficamos E d versus n y w z y encontró aproximadamente una dependencia inversa E d ≈ E 0 + a / ( w z - w 0 ) con E 0 =- 0.45eV, w 0 =4Å y a =4eVÅ. Este comportamiento es similar a la dependencia del ancho de la brecha de energía en el grafeno en zigzag y las nanocintas B-N [12,13,14,15, 43,44,45,46,47] que tienen origen de interacción electrón-electrón. Las nanocintas estrechas de HZZH InSe son semiconductores y se produce una transición de semiconductor a metal a medida que aumenta el ancho.

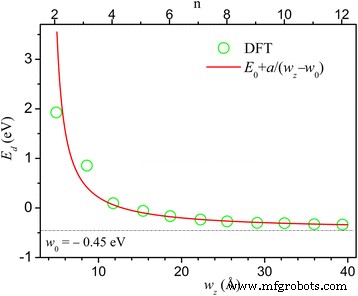
Las diferencias mínimas de energía E d entre los estados del borde derecho e izquierdo cerca de la energía de Fermi en n -Las nanocintas HZZH se muestran frente a n y w z . La curva de ajuste está en rojo

Las estructuras de bandas de n -KK y n -Las nanocintas HKKH no son sensibles al número de ancho n como se ejemplifica en la Fig. 4a, b, respectivamente, para n =4. En comparación con el borde en zigzag, el borde Klein desnudo tiene más uniones colgantes que dan como resultado un cambio significativo de la estructura de la banda. Los orbitales de los átomos de borde de Se generalmente tienen menor energía que los de los átomos de borde de In, similar a la nanocinta ZZ. En nanocintas HKKH, la supresión de p orbital de borde en átomos y el p orbital del átomo de borde de Se por la pasivación de átomos de H es obvio. Sin embargo, un átomo de H no es suficiente para pasivar todos los enlaces colgantes de los átomos del borde. Tanto las nanocintas KK como HKKH son metálicas.

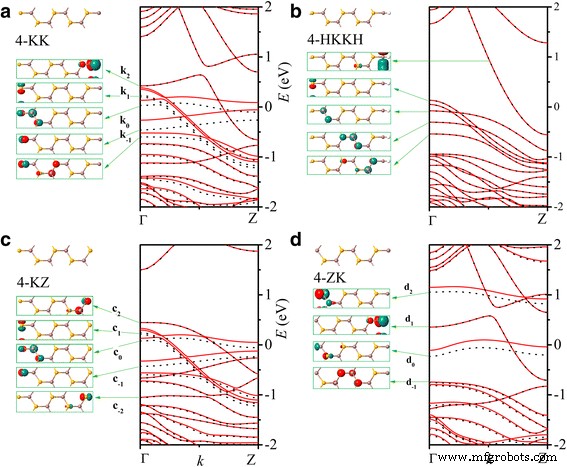
Las estructuras de bandas y los estados de Bloch de Γ puntos de 4-KK ( a ), 4-HKKH ( b ), 4-KZ ( c ) y 4-ZK ( d ) nanocintas

En nanocintas con una mezcla de zigzag y bordes de Klein, observamos una combinación de bandas de energía de los dos tipos de bordes cerca de la energía de Fermi. Como se muestra en la Fig. 4c para la nanocinta de 4 KZ, la dispersión y los estados de Bloch de puntos Γ de las bandas c 1 , c 0 y c −1 son los mismos que los de la banda k 1 , k 0 y k −1 en nanocintas de 4 KK como se muestra en la Fig. 4a, mientras que las bandas c 2 y c −2 son los mismos que la banda z 1 y z −2 de nanocintas 4-ZZ en la Fig. 2a. De manera similar, la estructura de la banda del nanocinta 4-ZK, como se ilustra en la Fig. 4d, está compuesta por la banda d 1 desde el borde derecho de Klein y las bandas d 2 , d 0 y d −1 desde el borde en zigzag izquierdo. Desde n -Las nanocintas -ZK y n-KZ mantienen parte de las bandas de energía de n -Nanocintas KK cercanas a la energía de Fermi, ambas son metálicas como n -Nanocintas KK. Por la misma razón, los bordes de mezcla de nanocintas pasivados con H, Z y K, también son metálicos.

Tanto las nanocintas AA como HAAH son semiconductores no magnéticos como se muestra en la Fig. 5a, b, donde las estructuras de banda se representan gráficamente para n =4, 5. La pasivación de los átomos de H puede mejorar la estabilidad estructural energéticamente y agranda la brecha energética. Curiosamente, la brecha de energía tiene una dependencia en zigzag del ancho de la nanocinta, mostrando un comportamiento familiar impar-par como en el grafeno y las nanocintas BN [10,11,12,13,14,15, 43,44,45,46, 47]. Como se ilustra en la Fig. 5c, n -Las nanocintas AA tienen un espacio (cuadrado verde oliva) más estrecho que el de la monocapa 2D InSe (guión rojo). El espacio aumenta (disminuye) monótonamente con el ancho para impar (par) n y converge a un valor de 1,15 eV en el límite de ancho grande cuando los dos bordes están desacoplados entre sí y estabilizan su energía [13]. Los estados de Bloch del máximo de la banda de valencia (VBM) en el punto Г y el mínimo de la banda de conducción (CBM) en el punto Z también se muestran en la Fig. 5c. El comportamiento de paridad se observa nuevamente con el simétrico ( n =5) o diagonal ( n =4, 6) distribución de los estados alrededor de átomos de borde de Se en VBM y alrededor de átomos de borde en CBM.

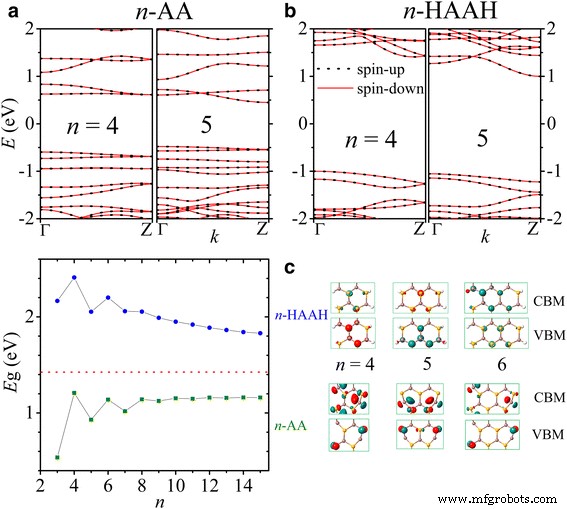
Las estructuras de bandas de las nanocintas de 4 y 5 AA se muestran en a y los de 4- y 5-HAAH en b . Las brechas de energía E g de n -AA (verde) y n -Las nanocintas HAAH (azules) se representan frente a n en c con el espacio de la monocapa de InSe (rojo) marcado. Los estados de Bloch en CBM y VBM para n =4, 5 y 6 se muestran en los paneles de la derecha de c

Por otro lado, las brechas de n -Las nanocintas HAAH (círculo azul) son más anchas que su contraparte 2D y disminuyen con el ancho para n pares e impares . En nanocintas pasivadas, los estados de Bloch en VBM y CBM tienen mucho menos componente de borde. Las brechas de energía correspondientes son aproximadamente 1 eV más anchas que las de las nanocintas desnudas, y la diferencia disminuye con el aumento de ancho [13].

En la Fig. 6a, mostramos la corriente-voltaje ( I - V ) característica de las nanocintas metálicas de InSe anteriores 4-ZZ (cuadrado), 4-KK (círculo) y 4-HKKH (triángulo). Las curvas de subida (bajada) están marcadas con símbolos rellenos (vacíos). Se ha empleado la fórmula de Landauer-Büttiker para calcular la corriente dependiente del espín I σ cuando una polarización de voltaje V b se aplica entre los electrodos L y R, con μ R = eV b / 2 y μ L =- eV b / 2 asumido. La resistencia diferencial negativa (NDR) y la polarización de espín se observan en nanocintas desnudas 4-ZZ y 4-KK bajo un sesgo en la región entre 0.5 y 1.2 V. La relación pico a valle de NDR es mayor que 10 para el 4- Nanoribbon ZZ debido al desajuste transversal de las funciones de onda entre las bandas de energía cerca de la energía de Fermi, como se ilustra en la Fig. 2a y se explica a continuación. Banda z 1 es el canal de transporte dominante en V b <1.2 V como lo indican los espectros de transmisión de giro hacia arriba y hacia abajo en la Fig. 6b, c, respectivamente. Sin embargo, las funciones de onda de la banda z 1 son ortogonales o están separados en el espacio de los de las bandas cercanas z 2 , z −1 yz −2 . Esto conduce a la discrepancia entre los estados z 1 en un electrodo y los de la misma energía en el otro electrodo bajo V b . Los electrones de la banda z 1 en un electrodo luego tienen dificultades para transportar al otro electrodo con conservación de energía. Como resultado, el I-V La curva de nanocintas 4-ZZ muestra una característica de banda única con fuerte NDR. Además, el spin split de la banda z 0 conduce a la polarización de espín en el régimen lineal. Sin embargo, en la nanocinta 4-HKKH pasivada, la corriente se satura en la región de sesgo NDR anterior.

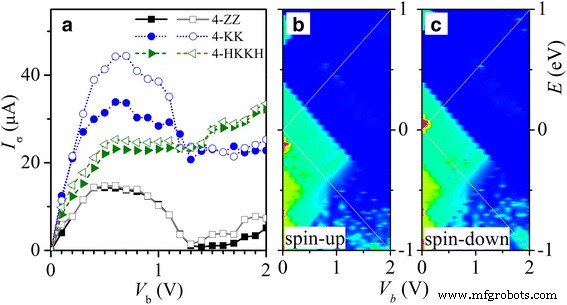
un El spin-up (lleno) y el spin-down (vacío) I - V Se presentan las características de las nanocintas InSe 4-ZZ (cuadrado), 4-KK (círculo) y 4-HKKH (triángulo). Los correspondientes espectros de transmisión de spin-up ( b ) y spin-down ( c ) se muestran para la nanocinta 4-ZZ. La ventana de transporte entre μ L y μ R está marcado por líneas blancas

Conclusiones

Hemos investigado sistemáticamente las propiedades electrónicas de las nanocintas InSe con bordes Z, A o K. Los bordes juegan un papel clave en la determinación de las propiedades, ya que los estados de electrones cercanos a la energía de Fermi tienen un gran peso de orbitales atómicos de borde. Los bordes desnudos Z y K son conductores y magnéticos. Una fuerte interacción borde-borde puede conducir a la transición de n -Nanocintas HZZH de semiconductores a metal como n aumenta. Como resultado, las nanocintas desnudas y pasivadas en H con bordes Z y K son metálicas, excepto las muy estrechas. n -AA y n -HAAH son semiconductores no magnéticos con brechas de energía más estrechas y más anchas, respectivamente, que las de la monocapa InSe. Sus brechas se acercan entre sí en zigzag como n aumenta, mostrando un comportamiento par-impar. Las curvas de corriente-voltaje de las nanocintas ZZ y KK se caracterizan por una fuerte polarización de espín y NDR de banda única.

Abreviaturas

1D:

Unidimensional

2D:

Bidimensional

A:

Sillón

CBM:

Banda de conducción mínima

K:

Klein

VBM:

Máximo de banda de valencia

Z:

Zigzag


Nanomateriales

  • Metal
  • Resina
  • fibra
  • Material compuesto
  • Nanomateriales
  • Materiales poliméricos
  • Biologicos
  • Teñir
  • Especias

    1. Características y usos de la aleación W-Ag
    2. Características y aplicaciones del titanio
    3. Características y aplicaciones del condensador de tantalio
    4. Óxido de hafnio y su estructura y aplicaciones
    5. Estructura cristalina y de valencia
    6. C Estructura y Función
    7. Estructura, características y aplicaciones del fotomultiplicador de silicio (SiPM)
    8. Tipos y características de la tela de fibra de vidrio
    9. Características y aplicaciones de la cinta adhesiva de fibra de vidrio
    10. Propiedades del aluminio y características de la aleación
    11. Diferencia entre estructura y unión.