Dos técnicas para linealizar puentes de sensores resistivos

Medir los minúsculos cambios de resistencia en los sensores resistivos puede ser una tarea abrumadora. A continuación, se muestran dos métodos de hardware para eliminar los errores de no linealidad del puente.

La resistencia de un sensor resistivo depende de una variable física como la temperatura o la fuerza. El cambio porcentual en la resistencia de estos dispositivos suele ser pequeño. Por ejemplo, el cambio total en la resistencia de una galga extensométrica puede ser inferior al 1% en todo su rango operativo.

Discernir estos pequeños valores exige circuitos de medición de alta precisión. Los circuitos puente nos permiten realizar estas medidas precisas con mayor facilidad. Sin embargo, la salida de un circuito puente puede tener una relación no lineal con la variable física medida incluso si estamos usando un sensor lineal.

En estos casos, podemos utilizar técnicas de software o hardware para eliminar los errores de no linealidad del puente. En este artículo, veremos dos técnicas diferentes de linealización de puentes de sensores resistivos.

Puente de no linealidad de sensores resistivos

Considere un sensor de presión resistiva con la siguiente respuesta lineal:

\ [R_ {sensor} =R_0 + Mx \]

donde R ₀ es la resistencia inicial del sensor a presión cero, x es el valor del mensurando (presión) y M es la pendiente de la respuesta del sensor. Para simplificar nuestras ecuaciones futuras, supongamos que el valor de M es igual al valor de la resistencia inicial del sensor (R ₀ ) y, por tanto, la respuesta del sensor es \ [R_0 (1 + x) \].

Por lo general, el cambio porcentual en la resistencia de un sensor resistivo es pequeño y necesitamos emplear un circuito de puente para realizar mediciones precisas más fácilmente. En la Figura 1 se muestra una configuración de puente común para este sensor.

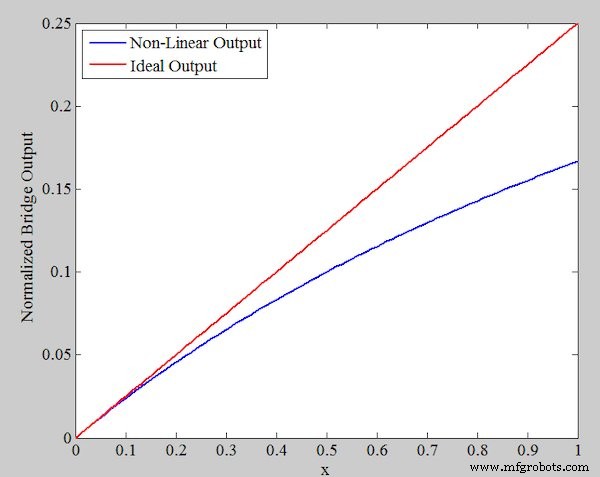
Figura 1. Configuración de puente común de un sensor resistivo

Tenga en cuenta que las otras tres resistencias del puente tienen una resistencia de R ₀ . Esta elección de resistencias de puente maximiza la sensibilidad de la salida (V _out ) a cambios en la resistencia del sensor. La ecuación de salida se puede obtener como:

\ [V_ {out} =V_A - V_B =V_r \ left (\ frac {R_0 (1 + x)} {R_0 + R_0 (1 + x)} - \ frac {1} {2} \ right) \]

Esto se simplifica a:

\ [V_ {out} =V_r \ left (\ frac {x} {2 (2 + x)} \ right) \]

Ecuación 1.

Como puede ver, la relación entre la salida del puente y el cambio en el valor de resistencia (x) no es lineal. Con \ [x \ ll2 \], podemos aproximar la ecuación anterior mediante la siguiente relación lineal:

\ [V_ {out} \ approx V_r \ left (\ frac {x} {4} \ right) \]

Ecuación 2.

La Figura 2 muestra la salida normalizada del puente \ [\ frac {V_ {out}} {V_r} \] tanto para el caso real (Ecuación 1) como para el resultado ideal (Ecuación 2).

Figura 2. Salidas no lineales (azul) e ideales (rojo) de las ecuaciones 1 y 2

Como era de esperar, la desviación de la respuesta lineal aumenta con x.

¿Cuánto error de no linealidad se introducirá?

Cuantifiquemos el error de no linealidad del circuito puente anterior. Podemos reescribir la Ecuación 1 como:

\ [V_ {out} =V_r \ left (\ frac {x} {4} \ right) \ left (\ frac {1} {1+ \ frac {x} {2}} \ derecha) \]

Suponiendo que \ [\ frac {x} {2} <<1 \], podemos usar el teorema de Taylor para obtener una aproximación de la función anterior como:

\ [V_ {out} =V_r \ left (\ frac {x} {4} \ right) \ left (1 - \ frac {x} {2} \ right) \]

Comparando este resultado con la Ecuación 2, podemos calcular la magnitud del error como:

\ [E_ {No linealidad} =V_r \ left (\ frac {x} {4} \ right) \ left (\ frac {x} {2} \ right) \]

Dividiendo esto por el valor ideal esperado dado por la Ecuación 2, podemos obtener el error de linealidad del punto final porcentual para un cambio dado en la resistencia (x):

\ [Porcentaje ~ Error =\ frac {x} {2} \ times 100 \% \]

Ejemplo de cálculo del error de no linealidad

Considere un sensor con respuesta \ [R_ {sensor} =R_0 (1 + x) \]. Suponga que \ [R_0 =100 ~ \ Omega \] y el valor máximo de x en todo el rango operativo es 0.01. El porcentaje máximo de error de linealidad será:

\ [Porcentaje ~ Error =\ left (\ frac {0.01} {2} \ right) \ times 100 \% =0.5 \% \]

Tenga en cuenta que, aunque podríamos utilizar software para eliminar los errores de linealidad del sensor, es deseable tener una respuesta lineal, ya que aumenta la precisión de la medición y facilita la calibración del sistema. Hay diferentes topologías de circuitos que se pueden utilizar para linealizar circuitos de puente.

En el resto de este artículo, examinaremos dos técnicas diferentes de linealización de puentes.

Método 1:Creación de un voltaje proporcional a los cambios de resistencia (x)

La primera técnica de linealización que analizaremos en este artículo se muestra en la Figura 3. Primero examinemos la idea básica de esta técnica y luego veamos cómo el circuito de la Figura 3 implementa esta idea.

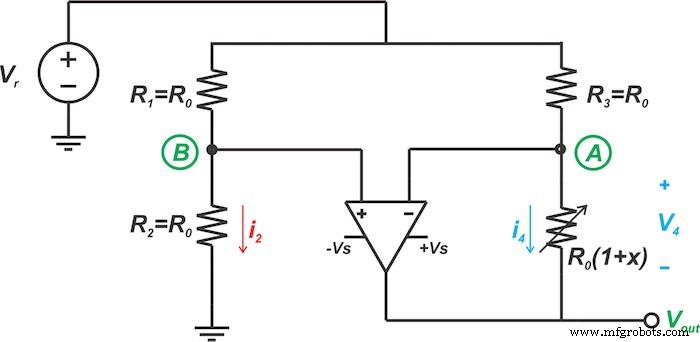
Figura 3. Un tipo de circuito para linealizar puentes de sensores resistivos

La Figura 4 muestra una representación de una corriente fija de \ [I_ {Ref} \] forzado a fluir a través de nuestro sensor lineal.

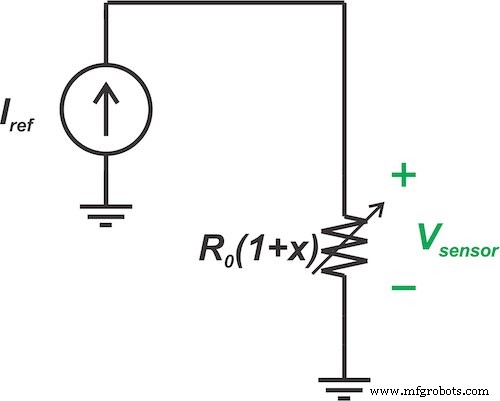
Figura 4. Una corriente fija (I _Ref ) forzado a través de un sensor lineal

En este escenario, el voltaje resultante a través del sensor sería:

\ [V_ {sensor} =I_ {Ref} \ times R_0 (1 + x) \]

que se puede reorganizar como:

\ [V_ {sensor} =R_0 \ times I_ {Ref} + R_0 \ times I_ {Ref} \ times x \]

Mientras que el primer término es un valor constante, el segundo término es proporcional a los cambios en la resistencia del sensor (x). Si podemos omitir el término constante, tendremos un voltaje que tiene una relación lineal con x.

Implementación del circuito

El circuito de la Figura 3 utiliza la idea anterior para linealizar el circuito puente. Dado que las entradas del amplificador operacional idealmente no consumen ninguna corriente, el voltaje en el nodo B tendrá un valor constante de:

\ [v_B =\ frac {R_0} {R_0 + R_0} V_r =\ frac {V_r} {2} \]

La retroalimentación negativa junto con la alta ganancia del amplificador operacional obligará a las entradas inversoras y no inversoras del amplificador operacional a tener el mismo voltaje:

\ [v_A =v_B =\ frac {V_r} {2} \]

Dado que ambos extremos de R3 están a potenciales constantes, fluirá una corriente constante a través de él. En otras palabras, el amplificador operacional hace que R3 actúe como una fuente de corriente que fuerza una corriente constante de \ [\ frac {V_r} {2R_0} \] en el sensor. Por lo tanto, el voltaje a través del sensor será:

\ [V_4 =\ frac {V_r} {2R_0} \ times R_0 (1 + x) =\ frac {V_r} {2} + \ frac {V_r} {2} x \]

El primer término es el valor constante que debe eliminarse de V _out ecuación. El segundo término es proporcional a los cambios de resistencia del sensor (x) y debería aparecer en la ecuación de salida. Aplicando la ley de voltaje de Kirchhoff, encontramos V _out como:

\ [V_ {out} =-V_4 + V_A =- \ left (\ frac {V_r} {2} + \ frac {V_r} {2} x \ right) + V_A \]

Por lo tanto, solo necesitamos V _A para ser igual a \ [\ frac {V_r} {2} \]. Esto ya está satisfecho, lo que conduce a:

\ [V_ {out} =- \ frac {V_r} {2} x \]

Por tanto, la salida tiene una relación lineal con x.

Método 2:Creación de una corriente proporcional a los cambios de resistencia (x)

La segunda técnica de linealización de puentes que analizaremos en este artículo se muestra en la Figura 5.

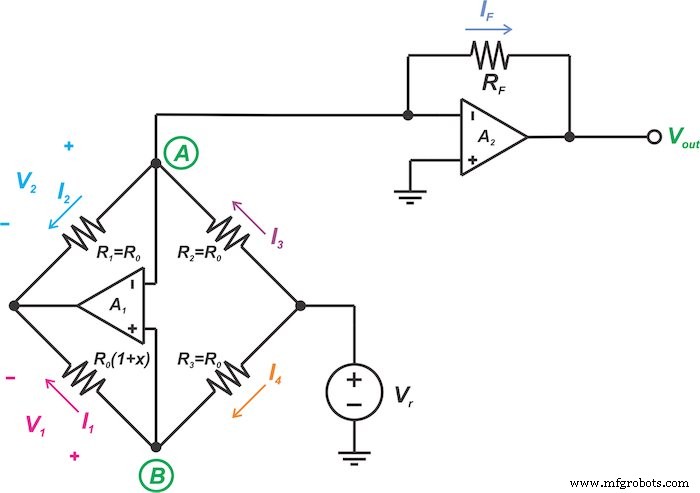
Figura 5. Otro circuito para la linealización analógica de puentes de sensores resistivos

De nuevo, echemos un vistazo a la idea básica de esta técnica y luego examinemos su implementación de circuito.

Esta segunda técnica de linealización se ilustra en la Figura 6.

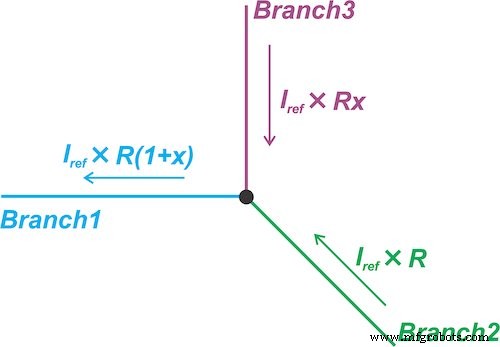
Figura 6. Técnica de linealización que obliga a que la corriente a través de una rama del circuito sea proporcional a la resistencia del sensor

Obliga a que la corriente a través de una rama del circuito (rama 1) sea proporcional a la resistencia del sensor:

\ [I_1 =I_ {Ref} \ times R_0 (1 + x) \]

donde yo _Ref es un valor constante. Luego, realiza la resta del dominio actual para eliminar el término constante \ [I_ {Ref} \ times R_0 \]. Con este fin, la corriente a través de la Rama 2 se establece en \ [I_ {Ref} \ times R_0 \]. Por lo tanto, la corriente a través de la Rama 3 será \ [I_ {Ref} \ times R_0x \] - proporcional a los cambios en la resistencia del sensor (x).

Implementación del circuito

Veamos cómo el circuito de la Figura 5 implementa la idea anterior. Nuevamente, la retroalimentación negativa junto con la alta ganancia de los amplificadores operacionales forzará las entradas inversoras y no inversoras de los dos amplificadores operacionales (ambos A ₁ y A ₂ ) para tener el mismo voltaje:

\ [v_A =v_B =0 \]

Ecuación 3.

Por lo tanto, tenemos V ₁ =V ₂ que lleva a

\ [R_0 (1 + x) \ times I_1 =R_0 \ times I_2 \]

Esto se simplifica a:

\ [I_2 =I_1 + I_1 \ times x \]

Ecuación 4.

Sabemos que yo ₁ =I ₄ y, teniendo en cuenta la Ecuación 3, tenemos:

\ [I_1 =I_4 =\ frac {V_r - v_A} {R_0} =\ frac {V_r} {R_0} \]

Sustituyendo esto en la Ecuación 4, obtenemos:

\ [I_2 =\ frac {V_r} {R_0} + \ frac {V_r} {R_0} \ times x \]

Por lo tanto, I ₂ es la suma de un valor constante y un término que es proporcional ax. Solo necesitamos usar la ley de la corriente de Kirchhoff para eliminar el término constante en la ecuación de la corriente de salida. La corriente a través de R2 genera una corriente igual a \ [\ frac {V_r} {R_0} \] al nodo A, lo que lleva a:

\ [I_F =- \ frac {V_r} {R_0} \ times x \]

Por tanto, obtenemos:

\ [V_ {out} =V_r \ times \ frac {R_F} {R_0} \ times x \]

El circuito de la Figura 5 necesita un amplificador operacional adicional en comparación con la primera técnica. Sin embargo, con las dos soluciones de amplificador operacional, podemos establecer arbitrariamente la ganancia eligiendo la relación \ [\ frac {R_F} {R_0} \].

Para ver una lista completa de mis artículos, visite esta página.

Los diodos láser permiten la detección de movimiento y las mediciones de distancia basadas en la luz (LiDAR) Seguimiento de activos de la cadena de frío