Energía en circuitos de CA resistivos y reactivos

Considere un circuito para un sistema de alimentación de CA monofásico, donde una fuente de voltaje de CA de 120 voltios y 60 Hz suministra energía a una carga resistiva:(Figura siguiente)

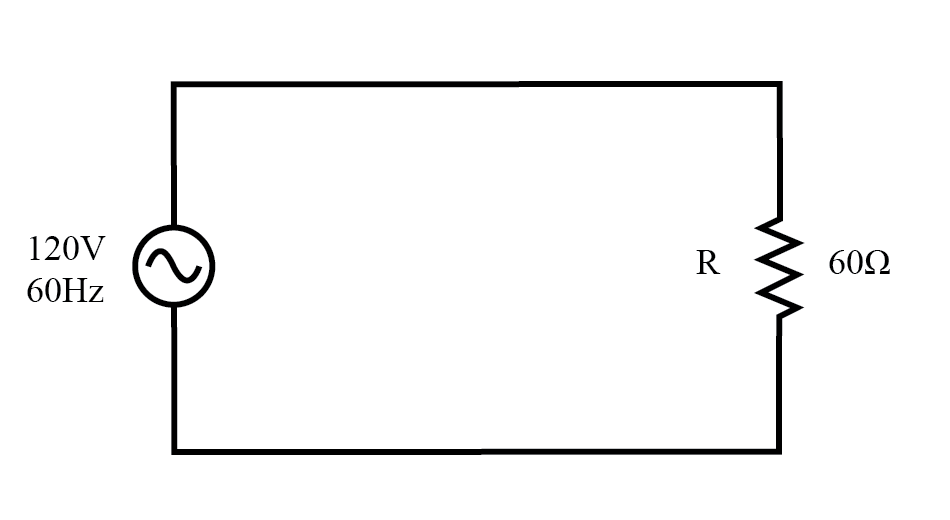
La fuente de CA impulsa una carga puramente resistiva.

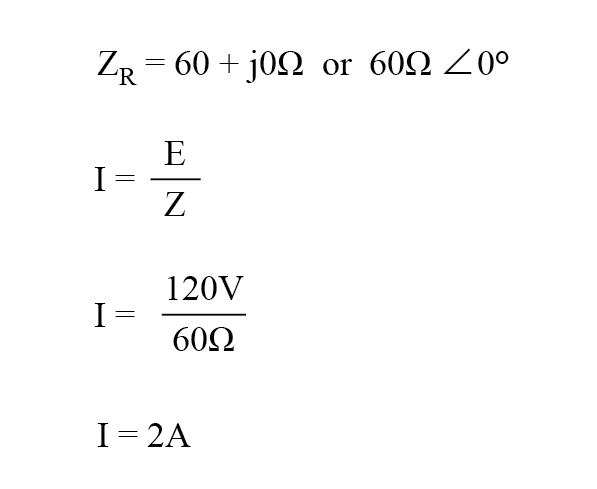
En este ejemplo, la corriente a la carga sería de 2 amperios, RMS. La potencia disipada en la carga sería de 240 vatios.

Debido a que esta carga es puramente resistiva (sin reactancia), la corriente está en fase con el voltaje y los cálculos son similares a los de un circuito de CC equivalente.

Si tuviéramos que trazar las formas de onda de voltaje, corriente y potencia para este circuito, se vería como la siguiente figura.

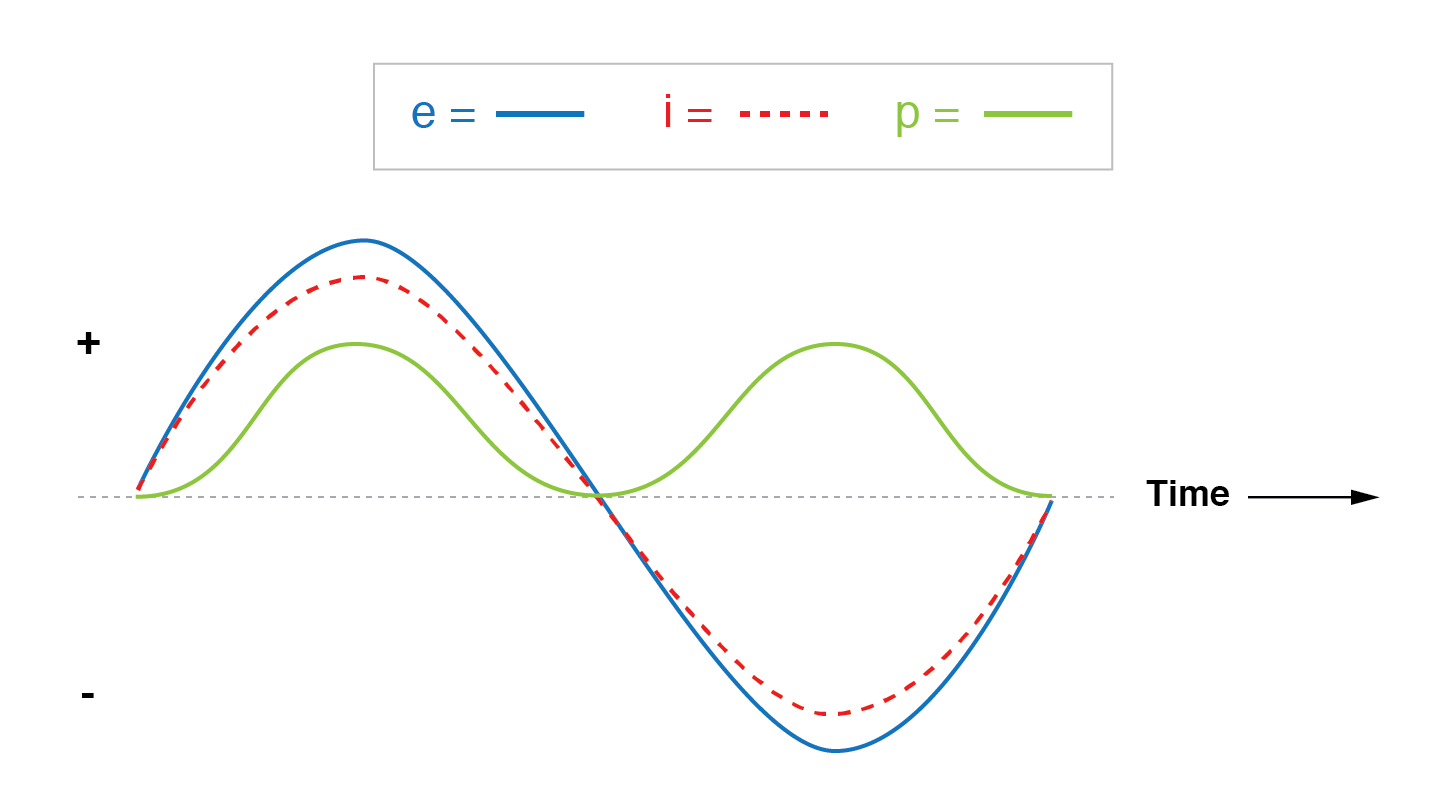
La corriente está en fase con el voltaje en un circuito resistivo.

Tenga en cuenta que la forma de onda de la potencia es siempre positiva, nunca negativa para este circuito resistivo.

Esto significa que la potencia siempre es disipada por la carga resistiva y nunca regresa a la fuente como ocurre con las cargas reactivas. Si la fuente fuera un generador mecánico, se necesitarían 240 vatios de energía mecánica (aproximadamente 1/3 de caballo de fuerza) para hacer girar el eje.

Además, tenga en cuenta que la forma de onda de la potencia no tiene la misma frecuencia que el voltaje o la corriente. Más bien, su frecuencia es doble el de las formas de onda de voltaje o corriente.

Esta frecuencia diferente prohíbe nuestra expresión de potencia en un circuito de CA usando la misma notación compleja (rectangular o polar) que se usa para voltaje, corriente e impedancia porque esta forma de simbolismo matemático implica relaciones de fase invariables.

Cuando las frecuencias no son las mismas, las relaciones de fase cambian constantemente.

Por extraño que parezca, la mejor manera de proceder con los cálculos de energía de CA es usar escalar notación y para manejar cualquier relación de fase relevante con trigonometría.

Circuito de CA con una carga puramente reactiva

A modo de comparación, consideremos un circuito de CA simple con una carga puramente reactiva en la figura siguiente.

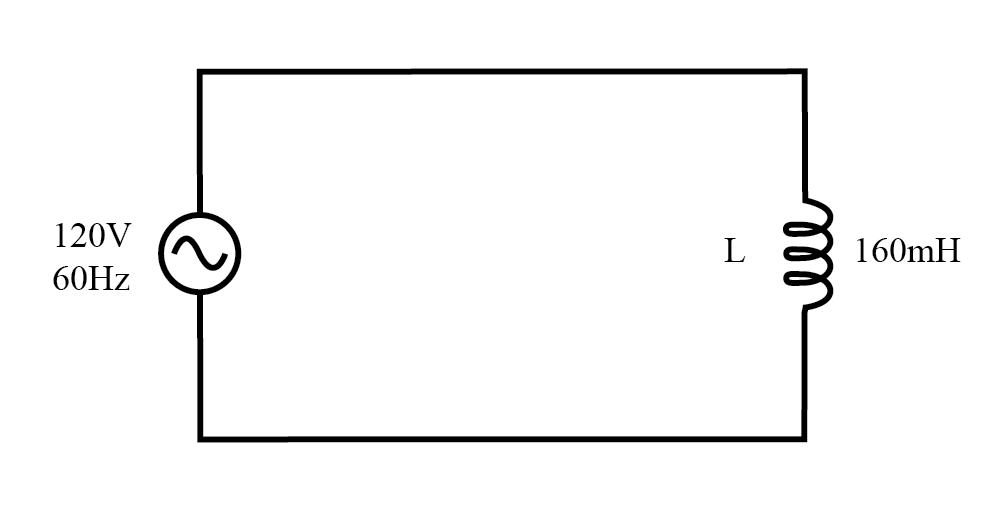
Circuito de CA con una carga puramente reactiva (inductiva).

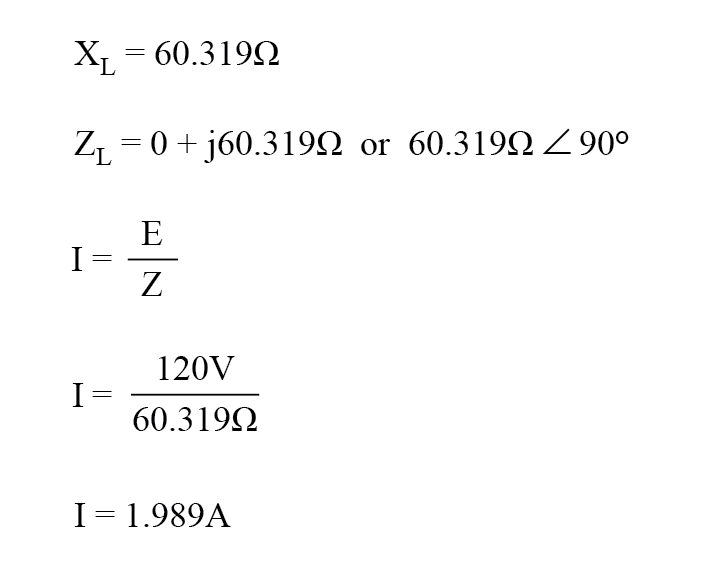
La energía no se disipa en una carga puramente reactiva. Aunque alternativamente se absorbe y se devuelve a la fuente.

Tenga en cuenta que la potencia alterna igualmente entre ciclos de positivo y negativo. (Figura anterior) Esto significa que la energía se absorbe y se devuelve alternativamente a la fuente.

Si la fuente fuera un generador mecánico, no se necesitaría (prácticamente) energía mecánica neta para hacer girar el eje, porque la carga no utilizaría energía.

El eje del generador sería fácil de girar y el inductor no se calentaría como lo haría una resistencia.

Circuito de CA con carga resistiva y puramente reactiva

Ahora, consideremos un circuito de CA con una carga que consta de inductancia y resistencia en la figura siguiente.

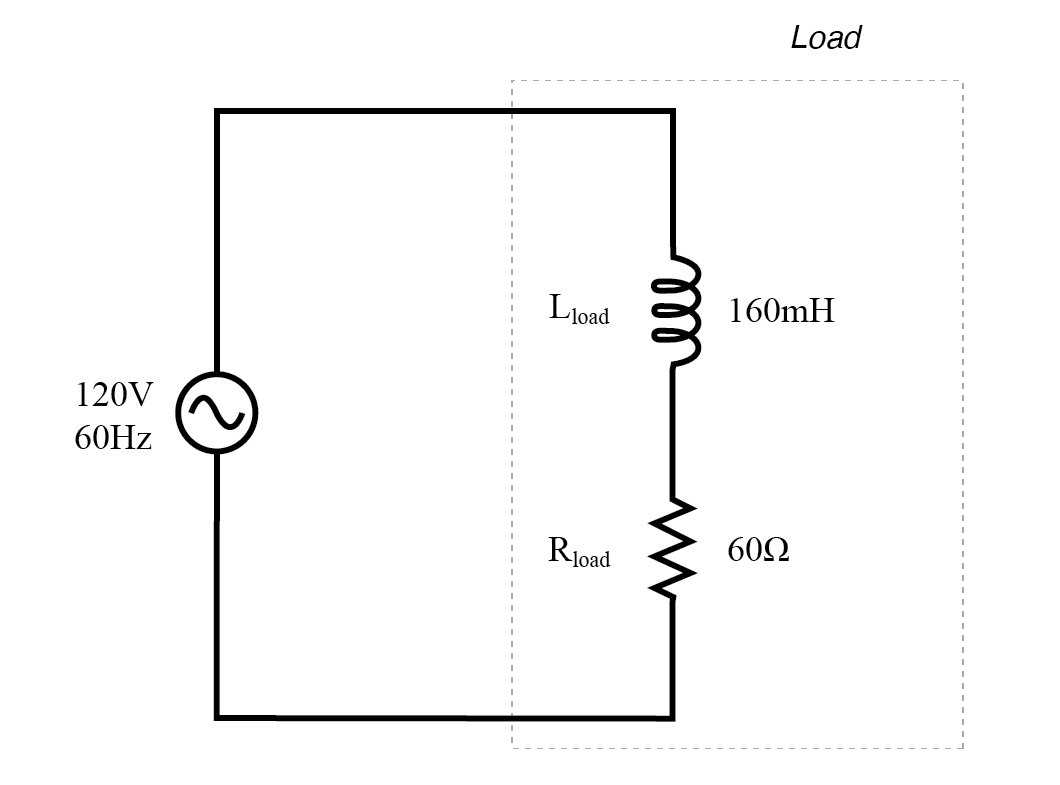
Circuito de CA con reactancia y resistencia.

A una frecuencia de 60 Hz, los 160 milihenrys de inductancia nos dan 60,319 Ω de reactancia inductiva.

Esta reactancia se combina con los 60 Ω de resistencia para formar una impedancia de carga total de 60 + j60.319 Ω, o 85.078 Ω ∠ 45.152 ^o . Si no nos preocupan los ángulos de fase (que no estamos en este punto), podemos calcular la corriente en el circuito tomando la magnitud polar de la fuente de voltaje (120 voltios) y dividiéndola por la magnitud polar de la impedancia. (85,078 Ω).

Con una tensión de alimentación de 120 voltios RMS, nuestra corriente de carga es de 1.410 amperios. Esta es la cifra que indicaría un amperímetro RMS si estuviera conectado en serie con la resistencia y el inductor.

Ya sabemos que los componentes reactivos disipan energía cero, ya que absorben energía del resto del circuito y la devuelven por igual.

Por lo tanto, cualquier reactancia inductiva en esta carga también disipará potencia cero.

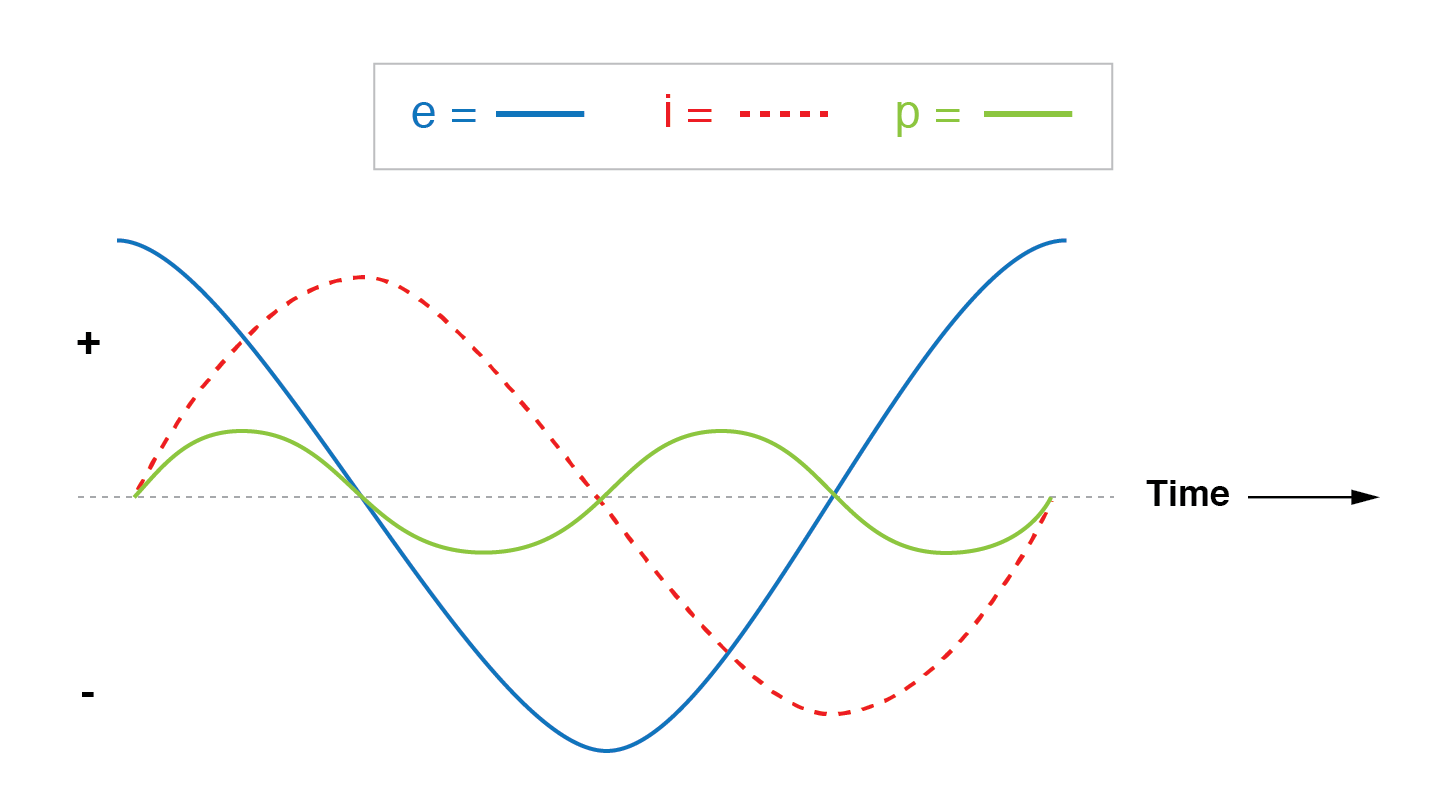
Lo único que queda para disipar la energía aquí es la parte resistiva de la impedancia de carga. Si observamos el gráfico de forma de onda de voltaje, corriente y potencia total para este circuito, vemos cómo funciona esta combinación en la figura siguiente.

Un circuito combinado resistivo / reactivo disipa más energía de la que regresa a la fuente. La reactancia no disipa energía; sin embargo, la resistencia lo hace.

Al igual que con cualquier circuito reactivo, la potencia alterna entre valores instantáneos positivos y negativos a lo largo del tiempo.

En un circuito puramente reactivo, la alternancia entre potencia positiva y negativa se divide por igual, lo que da como resultado una disipación de potencia neta de cero. Sin embargo, en circuitos con resistencia y reactancia mixtas como este, la forma de onda de potencia seguirá alternando entre positiva y negativa, pero la cantidad de potencia positiva superará la cantidad de potencia negativa.

En otras palabras, la carga inductiva / resistiva combinada consumirá más energía de la que regresa a la fuente.

Al observar el gráfico de forma de onda para la potencia, debería ser evidente que la onda pasa más tiempo en el lado positivo de la línea central que en el negativo, lo que indica que hay más potencia absorbida por la carga de la que regresa al circuito.

El poco retorno de potencia que se produce se debe a la reactancia; el desequilibrio de la potencia positiva frente a la negativa se debe a la resistencia, ya que disipa energía fuera del circuito (generalmente en forma de calor).

Si la fuente fuera un generador mecánico, la cantidad de energía mecánica necesaria para hacer girar el eje sería la cantidad de energía promediada entre los ciclos de energía positivo y negativo.

Representar matemáticamente la potencia en un circuito de CA es un desafío, porque la onda de potencia no tiene la misma frecuencia que el voltaje o la corriente.

Además, el ángulo de fase para la potencia significa algo bastante diferente del ángulo de fase para voltaje o corriente. Mientras que el ángulo de voltaje o corriente representa un cambio relativo en el tiempo entre dos ondas, el ángulo de fase para la potencia representa una relación entre energía disipada y energía regresada.

Debido a esta forma en que la potencia de CA difiere del voltaje o la corriente de CA, en realidad es más fácil llegar a cifras de potencia calculando con escalar cantidades de voltaje, corriente, resistencia y reactancia de lo que es para tratar de derivarlo de vector o complejo cantidades de voltaje, corriente e impedancia con las que hemos trabajado hasta ahora.

REVISAR:

• En un circuito puramente resistivo, toda la potencia del circuito es disipada por la (s) resistencia (s). El voltaje y la corriente están en fase entre sí.
• En un circuito puramente reactivo, la (s) carga (s) no disipa la potencia del circuito. Más bien, la energía se absorbe y se devuelve alternativamente a la fuente de CA. El voltaje y la corriente están desfasados ​​90 ° entre sí.
• En un circuito que consiste en una mezcla de resistencia y reactancia, habrá más potencia disipada por la carga que devuelta, pero parte de la potencia definitivamente se disipará y parte simplemente será absorbida y devuelta. El voltaje y la corriente en dicho circuito estarán desfasados ​​en un valor entre 0 ° y 90 °.

HOJA DE TRABAJO RELACIONADA:

• Hoja de trabajo de energía CA