Predicción de la temperatura máxima del canal en MOSFETs de Ga₂O₃: Un modelo analítico robusto

Resumen

En este trabajo se propone un modelo analítico preciso para la estimación de la temperatura máxima del canal de MOSFETs de Ga₂O₃ con sustratos nativos o de alta conductividad térmica. La conductividad térmica del Ga₂O₃ es anisotrópica y disminuye significativamente con el aumento de temperatura, ambos factores importantes para el comportamiento térmico de los MOSFETs de Ga₂O₃ y considerados en el modelo. Se realizan simulaciones numéricas mediante COMSOL Multiphysics para investigar la dependencia de la temperatura máxima del canal con la densidad de potencia variando parámetros geométricos del dispositivo y temperatura ambiente, mostrando buena concordancia con el modelo analítico, lo que valida este modelo. El nuevo modelo es instructivo para una gestión térmica eficaz de los MOSFETs de Ga₂O₃.

Antecedentes

Los transistores de efecto de campo metal-óxido-semiconductor (MOSFET) basados en óxido de galio (Ga₂O₃) son candidatos excelentes para la electrónica de potencia de próxima generación, beneficiándose de dos grandes ventajas del Ga₂O₃: banda prohibida significativamente alta (~ 4,8 eV) y cristales bulk de alta calidad producidos a bajo coste [1]. Se han dedicado enormes esfuerzos a mejorar sus propiedades eléctricas en todos los aspectos, como densidad de corriente [2], voltaje de ruptura [3] y figura de mérito de potencia [4]. Con la confirmación experimental de su potencial sin precedentes para dispositivos de electrónica de potencia [5-9], ahora es de suma importancia explorar el rendimiento y fiabilidad de los MOSFETs de Ga₂O₃, como el efecto de auto-calentamiento y, por tanto, la temperatura máxima del canal (T_max), debido a su conductividad térmica relativamente baja (κ, 0,11–0,27 Wcm⁻¹ K⁻¹ a temperatura ambiente) [1].

En años recientes, se han propuesto teórica y experimentalmente diversos métodos para estimar la T_max de MOSFETs de Ga₂O₃ [10-13]. En general, las simulaciones numéricas pueden estimar cuantitativamente la T_max de un dispositivo determinado, pero consumen mucho tiempo [14]. Por otro lado, la extracción de T_max mediante experimentos siempre se subestima [15]. Por ello, es necesario un modelo analítico que modele adecuadamente la T_max en MOSFETs de Ga₂O₃, proporcionando precisión suficiente con eficiencia temporal y evaluaciones cualitativas [14].

En este artículo se propone un modelo analítico de T_max para MOSFETs de Ga₂O₃ empleando la transformación de Kirchhoff, considerando la dependencia de κ con la temperatura y las direcciones cristalográficas del Ga₂O₃. El modelo propuesto se aplica a MOSFETs de Ga₂O₃ con sustratos nativos o de alta conductividad térmica. La validez y precisión del modelo analítico se verifican sistemáticamente mediante comparación con simulaciones numéricas mediante COMSOL Multiphysics.

Métodos y desarrollo del modelo

El modelo analítico para T_max en MOSFETs de Ga₂O₃ se propone basado en la estructura mostrada en la Fig. 1. Los parámetros clave de la estructura se listan en la Tabla 1. De hecho, se ha demostrado que el calentamiento Joule se concentra en el borde de drenaje de la compuerta en MOSFETs de Ga₂O₃ [13]. Para simplificar el modelo, se asume que el efecto de calentamiento desde la compuerta es uniforme [12] y puede penetrar completamente a través del óxido de compuerta debido a su grosor despreciable. Se consideran diferentes materiales de sustrato debajo del canal de Ga₂O₃, como Ga₂O₃ bulk y materiales de alta κ, buscando amplia factibilidad y compatibilidad. Así, el dispositivo se trata como un problema de dos capas. El sustrato contacta con un disipador de calor ideal, de modo que la superficie inferior es isotérmica y su temperatura iguala a la temperatura ambiente (T_amb, 300 K por defecto). Se imponen condiciones de frontera adiabáticas en las demás superficies de la estructura. Estas condiciones de frontera se resumen como [14, 16]:

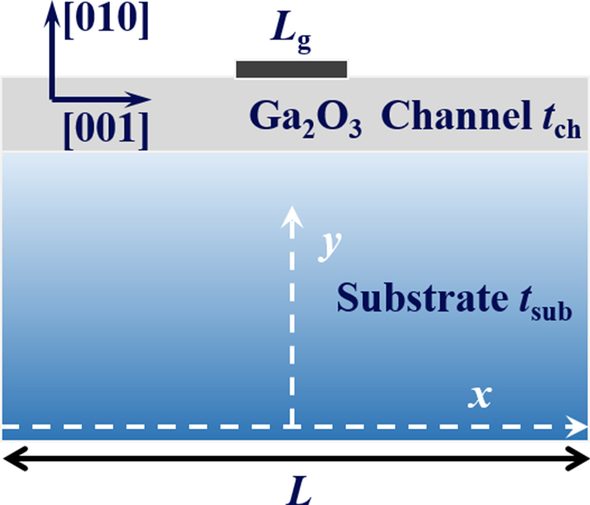
Diagrama esquemático del MOSFET de Ga₂O₃

$$\kappa_{y}\left.\frac{\partial T}{\partial y}\right|_{y=t_{ch}+t_{sub}} = \begin{cases} \frac{P}{L_{g}} & |x| \le \frac{L_{g}}{2} \\ 0 & |x| > \frac{L_{g}}{2} \end{cases}$$ (1)

$$\left.T\right|_{y=0} = T_{amb}$$ (2)

$$\left.\frac{\partial T}{\partial x}\right|_{x=-\frac{L}{2}} = \left.\frac{\partial T}{\partial x}\right|_{x=\frac{L}{2}} = 0$$ (3)

donde P, T y κ_y denotan la densidad de disipación de potencia, temperatura y conductividad térmica en dirección [010] para Ga₂O₃, respectivamente. Debe destacarse que la unidad de P es W/mm en este trabajo.

El valor de κ del Ga₂O₃, uno de los parámetros clave para la característica térmica del material, juega un papel importante en la difusión del efecto de calentamiento y en la precisión del modelo. Es decir, se requiere una descripción cuidadosa del valor de κ, debido a su seria anisotropía y dependencia de temperatura [17]. En general, la dependencia de κ del Ga₂O₃ con la temperatura (T) en dos orientaciones cristalinas diferentes ([001] y [010]) viene dada por:

$$\kappa_{[001]}(T) = 0,137 \times \left(\frac{T}{300}\right)^{-1,12}$$ (4)

$$\kappa_{[010]}(T) = 0,234 \times \left(\frac{T}{300}\right)^{-1,27}$$ (5)

Se realizó un estudio comparativo de T_max a diferentes P mediante COMSOL Multiphysics, considerando κ constante y realista, respectivamente. Se encontró que a P = 1 W/mm, se obtienen valores de T_max de 533 K y 622 K, respectivamente (no mostrados). Por tanto, es bastante necesario tener en cuenta los impactos de T y dirección cristalográfica en κ del Ga₂O₃ en el modelo.

El comportamiento térmico se rige por la ecuación de conducción de calor. La ecuación de conducción de calor en estado estacionario en el dominio de Ga₂O₃ es:

$$\frac{\partial}{\partial x}\left(\kappa_{x}(T)\frac{\partial T}{\partial x}\right) + \frac{\partial}{\partial y}\left(\kappa_{y}(T)\frac{\partial T}{\partial y}\right) = 0$$ (6)

donde κ_x denota la conductividad térmica en dirección [001] para Ga₂O₃. La ecuación no lineal de conducción de calor puede resolverse empleando la transformación de Kirchhoff. Sin embargo, la aplicación de la transformación de Kirchhoff puede verse restringida debido a la κ altamente anisotrópica en Ga₂O₃, siendo válida estrictamente solo para materiales con κ isotrópica [14]. Dada esta limitación, no se debe considerar κ_x y κ_y como dos variables independientes. La Figura 2 muestra la relación entre la resistividad térmica, es decir, 1/κ, y T para direcciones [001] y [010] en un amplio rango de T. Se observa que 1/κ_y puede sustituirse por 1/(cκ_x) y c se elige igual a 1,64. Consecuentemente, la Ec. (6) se transforma en:

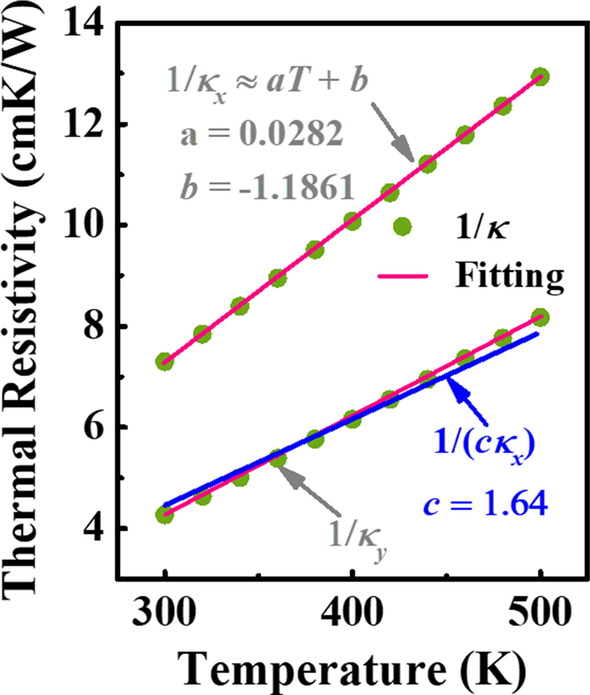
Relación entre la resistividad térmica y T para direcciones [001] y [010]. Símbolos verdes y líneas rojas denotan valores reales y ajustados, respectivamente. Línea azul representa la hipótesis 1/κ_y ≈ 1/(cκ_x), donde c = 1,64

$$\frac{\partial}{\partial x}\left(\kappa_{x}(T)\frac{\partial T}{\partial x}\right) + \frac{\partial}{\partial y}\left(c\kappa_{x}(T)\frac{\partial T}{\partial y}\right) = 0$$ (7)

Basado en las aproximaciones anteriores de κ_x y κ_y, la transformación de Kirchhoff puede emplearse sin restricciones. Además, se observa que el recíproco de κ se espera que sea proporcional a T. Para reducir la complejidad computacional, la expresión de 1/κ_x puede simplificarse como 1/κ_x = aT + b, como se muestra en la Fig. 2. El motivo del uso de a, b y c es solo comodidad para escribir las ecuaciones siguientes.

Mediante la aplicación de la transformación de Kirchhoff y el método de separación de variables, la expresión de T_max se deriva como:

$$\begin{aligned} T_{\text{max}} = & \\ & \left( T_{\text{amb}} + \frac{b}{a} \right)\exp\left( \frac{aP(t_{ch} + t_{sub})}{cL} + \frac{aPSL}{\sqrt{c} \pi^{2} L_{g}} \right) - \frac{b}{a}, \end{aligned}$$ (8)

donde

$$S = \sum_{n=1}^{\infty} \frac{\sin n\pi \frac{L_{g}}{L}}{n^{2}} \frac{\sinh 2n\pi \frac{t_{ch}+t_{sub}}{\sqrt{c}L}}{\cosh 2n\pi \frac{t_{ch}+t_{sub}}{\sqrt{c}L}}$$ (9)

Debe señalarse que S es una serie infinita convergente y su valor aproximado, que puede obtenerse fácilmente, se usa en el cálculo en lugar de su valor real.

En el caso de MOSFETs de Ga₂O₃ con sustratos de alta κ, la transformación de Kirchhoff no puede aplicarse directamente teóricamente. De hecho, para que la transformación sea válida, las condiciones de frontera deben ser isotérmicas (superficie T constante) o tener una densidad de flujo de calor fija. Sin embargo, debido a la diferente κ de Ga₂O₃ y material de sustrato, ninguna de estas condiciones se cumple completamente en la interfaz Ga₂O₃/sustrato. Considerando que la κ de Ga₂O₃ es mucho menor que la del sustrato de alta κ, se introduce la hipótesis de interfaz isotérmica entre Ga₂O₃ y sustrato. Esta hipótesis es instrumental para derivar la expresión de T_max y su validez se verificará después. En este caso, la resistencia térmica (R_TH) del sustrato de alta κ, razón entre la diferencia de T_int y T_amb y PW, es decir, R_TH = (T_int—T_amb) / (PW), puede calcularse como R_TH = LW/(κt_sub), donde W es el ancho del sustrato [19]. Así, la expresión de la temperatura de la interfaz Ga₂O₃/sustrato (T_int) es:

$$T_{int} = \frac{P t_{sub}}{\kappa_{sub} L} + T_{amb}$$ (10)

donde κ_sub es la conductividad térmica del sustrato heterogéneo, asumida constante. Además, debe señalarse que la resistencia térmica de frontera entre Ga₂O₃ y sustratos heterogéneos no se incluye en el modelo. Por tanto, con ayuda de la Ec. (8), la expresión de T_max para MOSFETs de Ga₂O₃ con sustrato heterogéneo se deriva como:

$$\begin{aligned} T_{\text{max}} = & \\ & \left( T_{\text{int}} + \frac{b}{a} \right)\exp\left( \frac{aP t_{ch}}{cL} + \frac{aPSL}{\sqrt{c} \pi^{2} L_{g}} \right) - \frac{b}{a}, \end{aligned}$$ (11)

donde

$$S = \sum_{n=1}^{\infty} \frac{\sin n\pi \frac{L_{g}}{L}}{n^{2}} \frac{\sinh 2n\pi \frac{t_{ch}}{\sqrt{c}L}}{\cosh 2n\pi \frac{t_{ch}}{\sqrt{c}L}}$$ (12)

Resultados y discusión

La validez del modelo analítico para T_max en MOSFETs de Ga₂O₃ se verificó sistemáticamente en esta sección, considerando tanto sustrato nativo como su contraparte con mayor conductividad térmica. La mejor forma de probar la validez de un modelo es contra datos experimentales. Sin embargo, no se encontraron algunos parámetros geométricos clave en la literatura experimental, como t_sub y L en Ref. [12]. Por tanto, se usa simulación de elementos finitos, uno de los medios más precisos, para verificar nuestro modelo. La Figura 3 muestra la dependencia de T_max con la densidad de potencia P obtenida tanto de COMSOL Multiphysics como del modelo analítico, para MOSFET de Ga₂O₃ con sustrato nativo. Se consideran parámetros clave variados, incluyendo longitud del dispositivo L, grosor de sustrato t_sub y temperatura ambiente T_amb. Como se muestra en la Fig. 3a, T_max aumenta naturalmente con la densidad de potencia elevada y la tasa de aumento se acelera con L menor. Esto se atribuye a que el dispositivo con L mayor permite disipación de calor desde la región activa y, por tanto, su temperatura global es menor que la de L menor a mismo P [11]. Es decir, su R_TH, la pendiente de las curvas, es menor que la de este último. Además, como κ de Ga₂O₃ disminuye con el aumento de temperatura global, su R_TH también aumentará más lentamente que el de L menor, lo cual es evidente en la Fig. 3a [19]. De igual modo, se investigó la dependencia de T_max respecto a t_sub, como se ilustra en la Fig. 3b. Se observa que la tendencia de T_max respecto a P es la misma que en la Fig. 3a. El sustrato más delgado siempre produce un aumento atenuado de T_max sobre la densidad de potencia aumentada, lo cual es comprensible: sustrato más delgado, temperatura global menor, R_TH menor y su tasa de aumento, igual que el análisis en Fig. 3a. La Figura 3c compara la influencia de T_amb en T_max a medida que P aumenta. Es evidente que la diferencia entre las dos curvas aumenta lentamente, lo cual difiere de las Figs. 3a, b. Normalmente, R_TH está dominado por parámetros geométricos del dispositivo y el valor de κ del material. Sin embargo, considerando que la estructura es fija en este caso, el aumento de R_TH solo es inducido por la disminución de κ de Ga₂O₃. Por otro lado, se observa un alto nivel de concordancia para el modelo propuesto, que considera la relación T- y dirección-dependiente para κ de Ga₂O₃, confirmando la naturaleza escalable del modelo. En promedio, la diferencia entre el modelo propuesto y la simulación es < 1 K. La excelente concordancia general observada sugiere que el modelo propuesto es altamente efectivo y preciso.

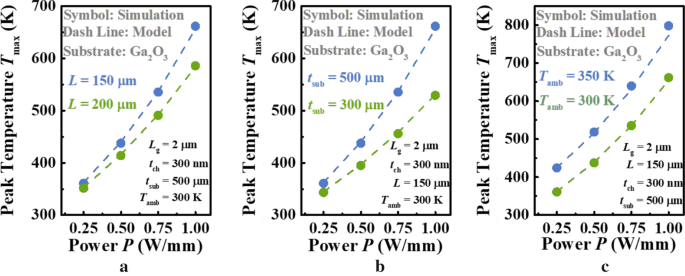
Dependencia de T_max con a la longitud del dispositivo L, b el grosor de capa de sustrato t_sub, y c temperatura ambiente T_amb a diferentes potencias P. Símbolos y líneas denotan resultados del modelo propuesto y simulación, respectivamente

Asimismo, como se muestra en la Fig. 4, se repiten comparaciones similares para MOSFETs de Ga₂O₃ sobre sustrato de alta κ, SiC. Aquí, los pasos para L y T_amb que elegimos son mayores que los de la Fig. 3, y se considera el grosor de canal t_ch variable en lugar de t_sub en este caso. De lo contrario, la diferencia entre las dos curvas de T_max respecto a P en cada figura sería indistinguible, debido a la eficiente capacidad de disipación de calor del sustrato SiC. La κ de SiC (3,7 Wcm⁻¹ K⁻¹) aplicada es un parámetro por defecto en COMSOL Multiphysics. Gracias a la alta κ de SiC, se ve claramente en todas las figuras que el aumento de T_max es aproximadamente lineal a medida que P aumenta, lo que significa que la influencia de la temperatura en R_TH del dispositivo es despreciable. Debe señalarse que nuestro modelo puede describir esta relación lineal con éxito. Sin embargo, es obvio que T_max calculado por el modelo actual es menor que el predicho por simulación, y esta diferencia es más evidente con el aumento del consumo de potencia. Para mostrar este mecanismo, se extraen T_int simulados con el aumento de potencia y se comparan con T_int calculados por la Ec. (10) como se grafica en la Fig. 5. Se encuentra que el calentamiento Joule se concentra más en el centro del dispositivo a medida que P aumenta. Hay 0,5 K y 4 K de ΔT entre el modelo y la simulación en esta ubicación cuando P = 0,25 y 1 W/mm, respectivamente. Esta es la razón por la que nuestro modelo no predice T_max con precisión. Por tanto, se necesita una hipótesis más razonable de T_int para obtener mayor precisión en el futuro. No obstante, T_max es predicho por el modelo solo < 4 K menor que el de simulación incluso bajo 1 W/mm de densidad de disipación de potencia. Es decir, aunque la hipótesis de T_int uniforme es inconsistente con la realidad, nuestro modelo puede proporcionar una estimación de T_max con suficiente precisión.

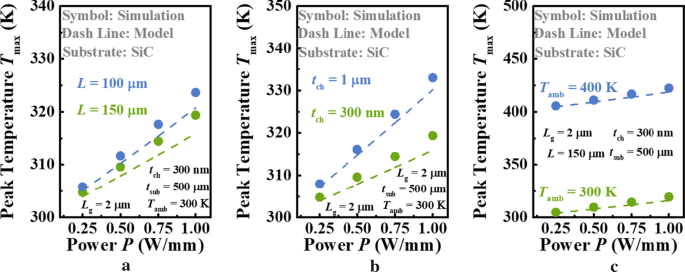
Dependencia de T_max de MOSFETs de Ga₂O₃ con sustrato SiC en a la longitud del dispositivo L, b el grosor de capa de Ga₂O₃ t_ch, y c temperatura ambiente T_amb a diferentes potencias P. Símbolos y líneas denotan resultados del modelo propuesto y simulación, respectivamente

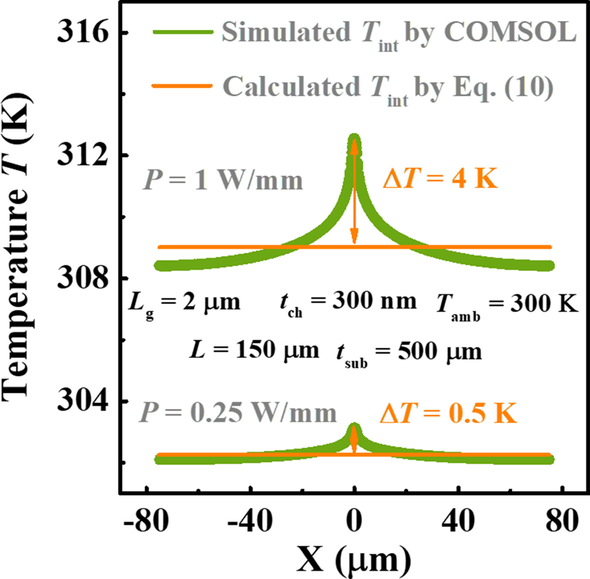
Comparación de T_int entre simulado y calculado por Ec. (10) a diferentes P

Conclusiones

Se presenta un modelo analítico preciso para estimar T_max de MOSFETs de Ga₂O₃ que involucra la dependencia de la conductividad térmica con la temperatura y la dirección. Se ha derivado una expresión simple basada en geometría del dispositivo y parámetros de material. Se ha obtenido una excelente concordancia entre el modelo y simulaciones numéricas COMSOL Multiphysics variando diferentes consumos de potencia. El modelo propuesto para T_max es de gran importancia para la gestión térmica eficaz de dispositivos de potencia, especialmente MOSFETs de Ga₂O₃.

Disponibilidad de datos y materiales

Los conjuntos de datos que apoyan las conclusiones de este artículo están incluidos dentro del artículo.

Abreviaturas

Ga₂O₃:

Óxido de galio

MOSFETs:

Transistores de efecto de campo metal-óxido-semiconductor

AlGaN:

Nitruro de aluminio y galio

GaN:

Nitruro de galio

SiC:

Carburo de silicio