Cálculo de energía eléctrica

Aprenda la fórmula del poder

Hemos visto la fórmula para determinar la potencia en un circuito eléctrico:multiplicando el voltaje en "voltios" por la corriente en "amperios" llegamos a una respuesta en "vatios". Apliquemos esto a un ejemplo de circuito:

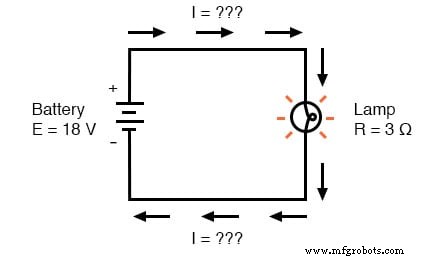
Cómo utilizar la ley de Ohm para determinar la corriente

En el circuito anterior, sabemos que tenemos un voltaje de batería de 18 voltios y una resistencia de lámpara de 3 Ω. Usando la ley de Ohm para determinar la corriente, obtenemos:

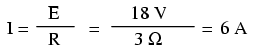
Ahora que conocemos la corriente, podemos tomar ese valor y multiplicarlo por el voltaje para determinar la potencia:

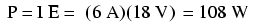
Esto nos dice que la lámpara está disipando (liberando) 108 vatios de potencia, muy probablemente en forma de luz y calor.

Aumento del voltaje de la batería

Intentemos tomar el mismo circuito y aumentar el voltaje de la batería para ver qué sucede. La intuición debería decirnos que la corriente del circuito aumentará a medida que aumenta el voltaje y la resistencia de la lámpara permanece igual. Asimismo, la potencia también aumentará:

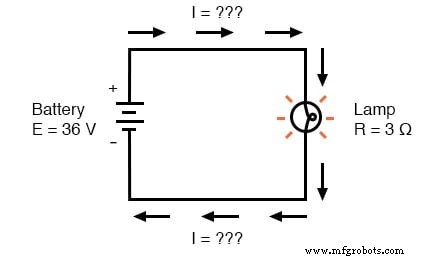
Ahora, el voltaje de la batería es de 36 voltios en lugar de 18 voltios. La lámpara sigue proporcionando 3 Ω de resistencia eléctrica al flujo de corriente. La corriente es ahora:

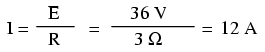
Esto es lógico:si I =E / R, y duplicamos E mientras R permanece igual, la corriente debería duplicarse. De hecho, tiene:ahora tenemos 12 amperios de corriente en lugar de 6. Ahora, ¿qué pasa con la potencia?

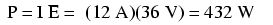
¿Qué efecto tiene el aumento del voltaje de una batería en la energía?

Observe que la potencia ha aumentado tal como podríamos haber sospechado, pero aumentó bastante más que la actual. ¿Por qué es esto? Debido a que la potencia es una función del voltaje multiplicado por la corriente, y ambos voltaje y corriente duplicados de sus valores anteriores, la potencia aumentará en un factor de 2 x 2, o 4.

Puede verificar esto dividiendo 432 vatios por 108 vatios y viendo que la relación entre ellos es de hecho 4. Usando álgebra nuevamente para manipular la fórmula, podemos tomar nuestra fórmula de potencia original y modificarla para aplicaciones donde no conocemos tanto el voltaje y corriente:si solo conocemos el voltaje (E) y la resistencia (R):

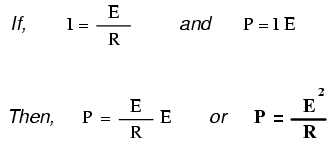
Si solo conocemos la corriente (I) y la resistencia (R):

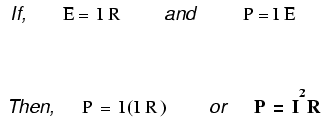
Ley de Joule vs. Ley de Ohm

Una nota histórica:fue James Prescott Joule, no Georg Simon Ohm, quien descubrió por primera vez la relación matemática entre la disipación de potencia y la corriente a través de una resistencia. Este descubrimiento, publicado en 1841, siguió la forma de la última ecuación (P =I ² R), y se conoce propiamente como Ley de Joule.

Sin embargo, estas ecuaciones de potencia se asocian tan comúnmente con las ecuaciones de la Ley de Ohm que relacionan voltaje, corriente y resistencia (E =IR; I =E / R; y R =E / I) que con frecuencia se atribuyen a Ohm.

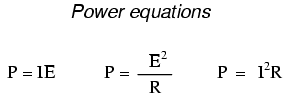
REVISAR:

• Potencia medida en vatios , simbolizado por la letra "W".
• Ley de Joule:P =I ² R; P =IE; P =E ² / R

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de energía

Pruebe nuestra Calculadora de la ley de Ohm en nuestra sección de Herramientas.