Modelado de ADC mediante polinomio de intermodulación y número efectivo de bits

En este artículo, discutimos otra metodología sobre cómo modelar ADC en simulaciones de sistemas, esta vez usando el número efectivo de bits y también ajustando nuestro ADC introduciendo un polinomio de quinto orden en la entrada ideal del cuantificador.

Hasta ahora en esta serie, hemos discutido los méritos de varias formas de modelar convertidores de datos en simulaciones de sistemas, particularmente mediante el uso de un método de modelado utilizando el número efectivo de bits o ENOB.

Ahora, continuaremos esta discusión agregando un nuevo elemento:ajustando nuestro modelo ADC directamente con un polinomio de quinto orden agregado a la entrada ideal del cuantificador.

Descripción de nuestro nuevo modelo ADC

El modelo presentado en nuestro artículo anterior no dio como resultado ninguna frecuencia espuria distinta (espuelas). Dado que las espuelas son una característica importante del desempeño de ADC, se requería un modelo mejor.

Esto se muestra en la Figura 1.

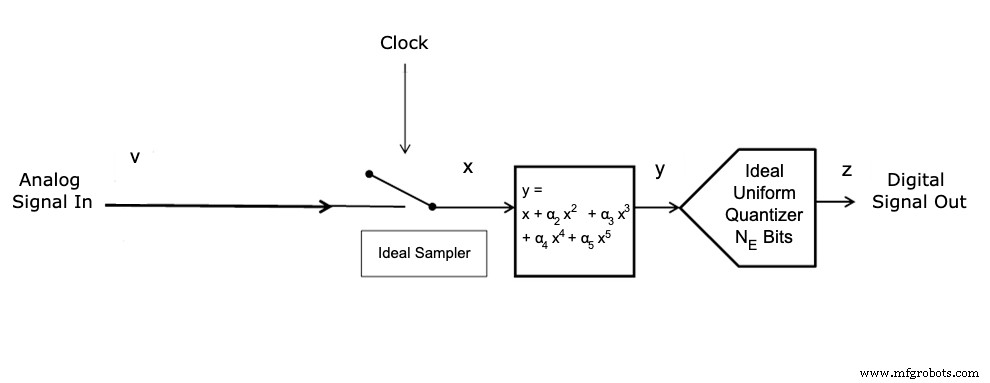
Figura 1.

Esto agrega un polinomio de quinto orden a la entrada ideal del cuantificador.

Se debe utilizar una entrada de dos tonos para determinar los parámetros α _i (f _c ) y N _E (f _c ); donde f _c es la frecuencia central entre los tonos, como se muestra en la Figura 2 (que reconocerá como la Figura 4 de nuestro primer artículo).

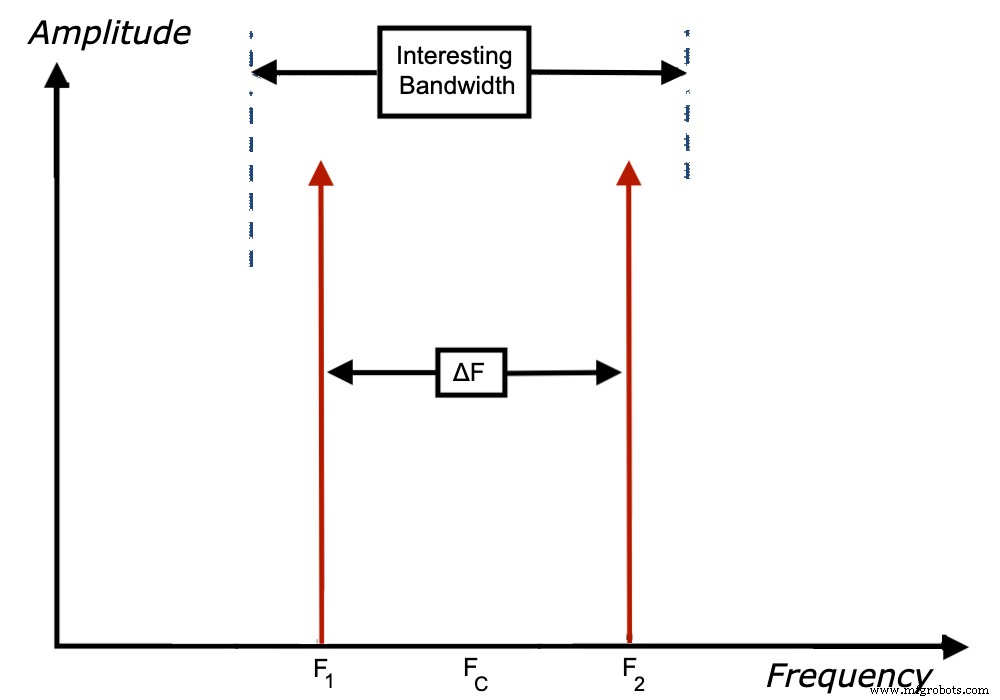
Figura 2.

Si alguno de estos parámetros también es función de Δf, la separación entre los tonos, probablemente haya una no linealidad con la memoria en el ADC, y este modelo no se aplicaría.

Como ejemplo, se utilizó la misma entrada de dos tonos que se muestra en la Figura 3 (discutida como la Figura 3 de nuestro artículo anterior), con N _E =8 bits, α ₃ =0.04, y todas las demás α _i =0. Existe el mismo ancho de banda de Nyquist (730,9 MHz) y "ancho de banda interesante" (233,7 MHz) que en nuestro artículo anterior.

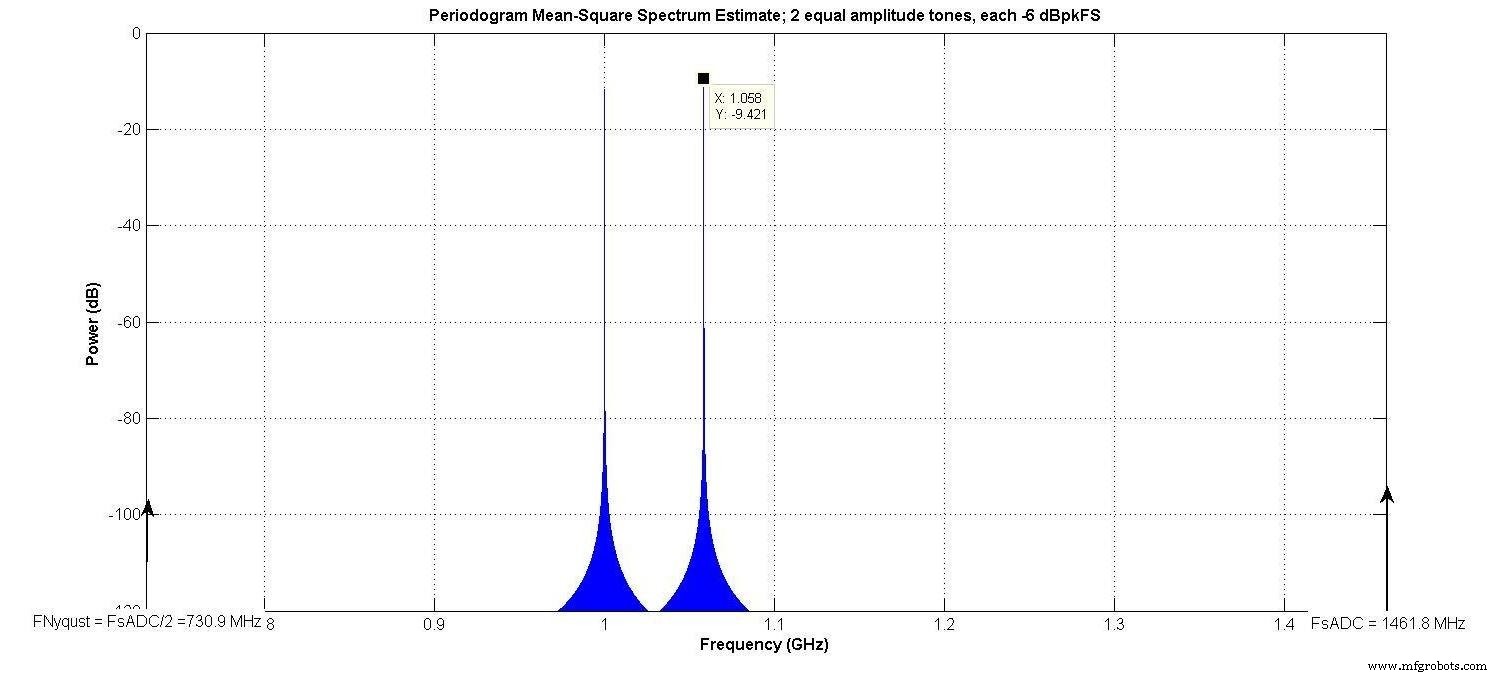
Figura 3.

La Figura 4 muestra la salida con entrada de un tono y la Figura 5 muestra la salida con entrada de dos tonos.

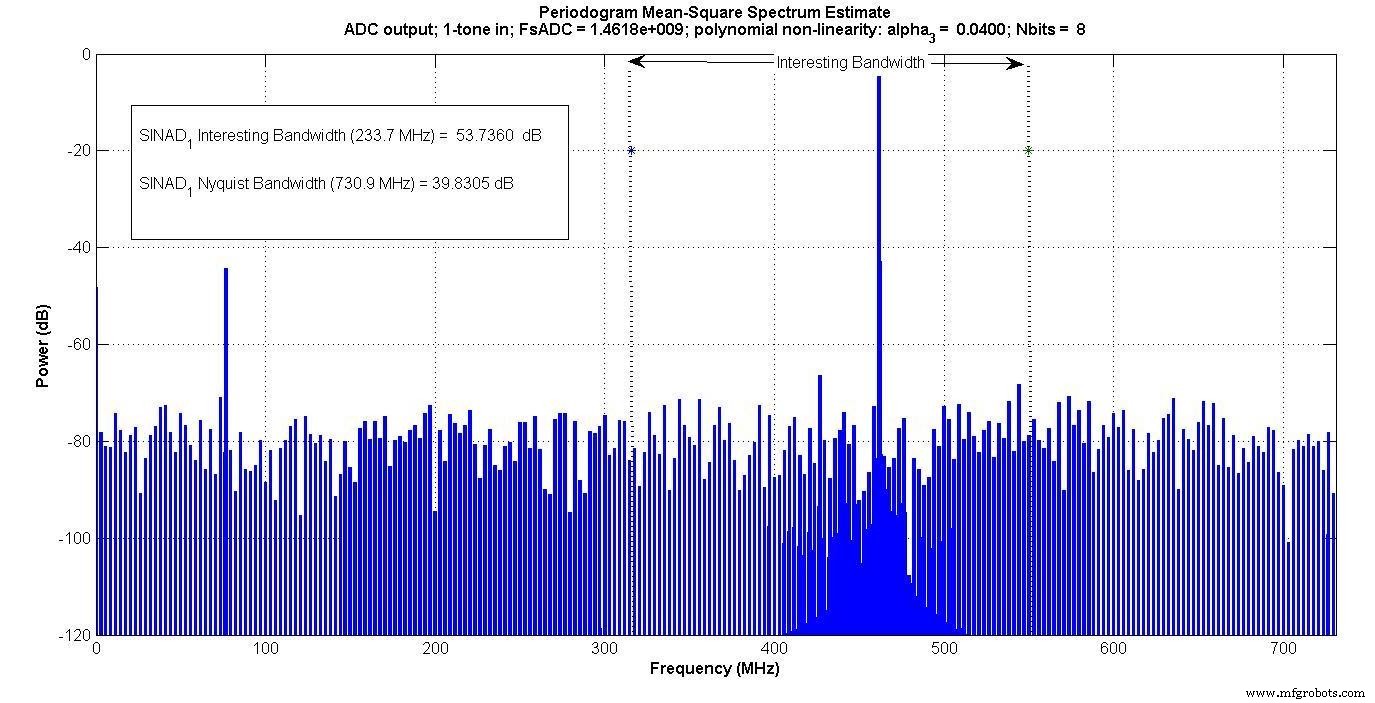
Figura 4.

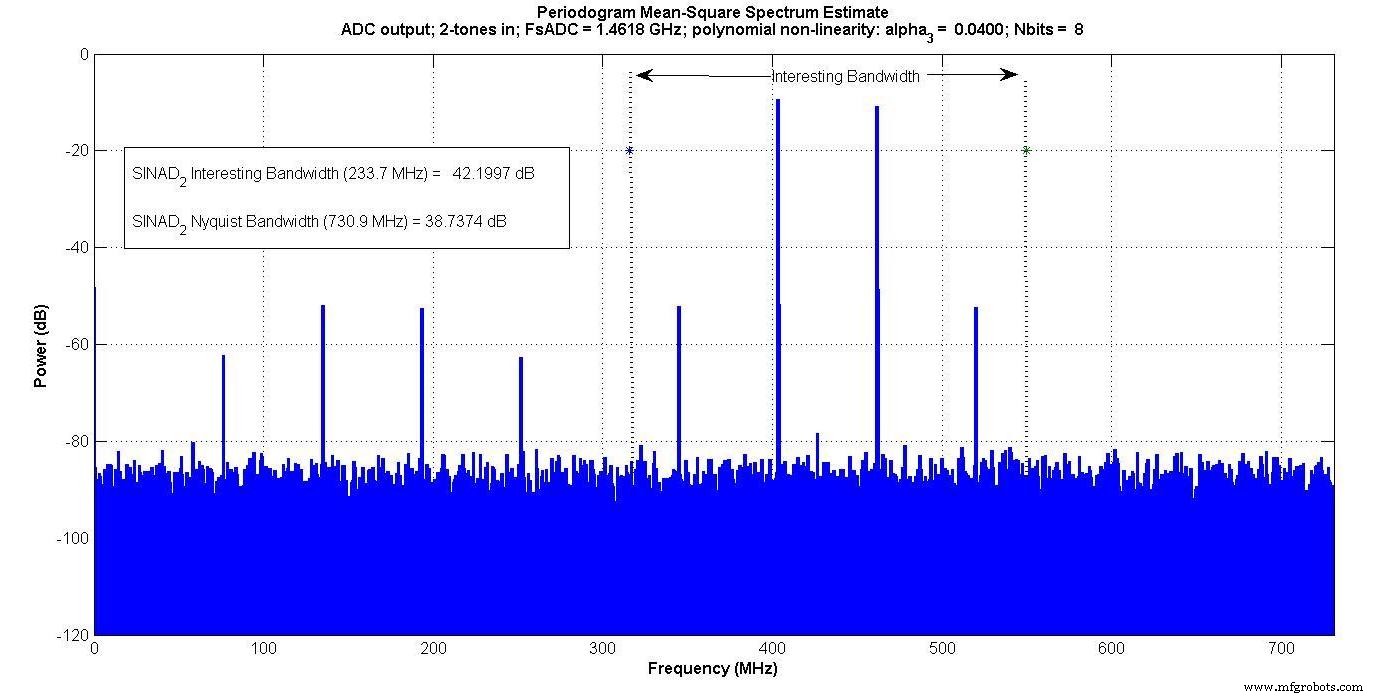
Figura 5.

Los productos de intermodulación aparecen dentro del "ancho de banda interesante" para la entrada de dos tonos, pero no para la entrada de un tono.

Si alguien solo estuviera midiendo dentro de este "ancho de banda interesante", por ejemplo, si hubiera un filtro de paso de banda digital que solo pasara esa banda, la prueba de un tono no capturaría el efecto de intermodulación, pero el de dos tonos sí lo haría.

La Figura 6 traza los distintos SINAD para 5 a 12 bits de entrada. Es evidente que la entrada de un tono, medida en el "ancho de banda interesante", no captura el efecto de intermodulación durante más de 7 bits.

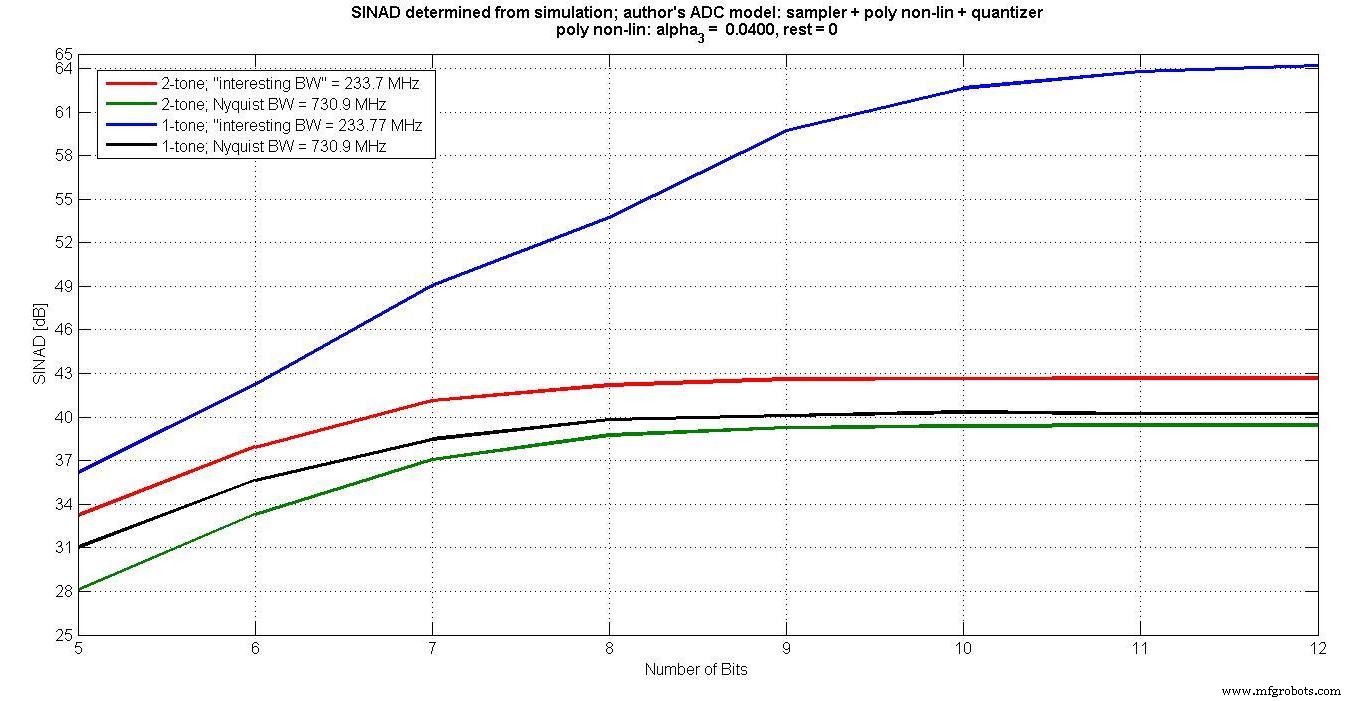
Figura 6.

Además, para más de 7 bits, dado que el ruido de cuantificación disminuye a medida que aumenta el número de bits, pero la distorsión de intermodulación permanece igual, el SINAD no mejora con más bits.

Comparación con el modelo de fabricantes

Estimado lector:Puede que ahora se esté preguntando; "¿Y qué? Estos son solo algunos modelos y sus respuestas a algunas señales. ¿Cuál es el propósito? ”

El propósito debe ser que se puedan realizar mediciones de dos tonos en un ADC y que los valores de los parámetros que se muestran en la Figura 1 se seleccionen para que se ajusten mejor a la salida del ADC medida. A menudo, esto se puede hacer ajustándolos manualmente hasta que se obtenga un buen ajuste. Luego, el modelo simplificado se puede utilizar en simulaciones de tasa de error de bits larga (BER).

Las mediciones se pueden realizar en un dispositivo real, en un buen modelo para el dispositivo o se pueden obtener de las hojas de datos de los fabricantes.

Para ser un buen modelo, debe aproximarse mucho al dispositivo real; como un modelo SPICE completo. Un modelo tan complicado tardaría demasiado en ejecutarse en una simulación BER.

Lo que estaba disponible para su autor de un fabricante era lo que llamaron un modelo "conductual", que, según afirmaron, capturaba todos los parámetros importantes de un modelo de ADC en particular. El modelo del fabricante también tuvo en cuenta la fluctuación del reloj tanto interna como externa. Esto se utilizó para evaluar el método.

Entrada de dos tonos

La Figura 7 muestra la configuración de la simulación. Se generó la entrada de dos tonos y luego se introdujo en el modelo del autor y del fabricante. Ambos se mostraron con análisis espectral.

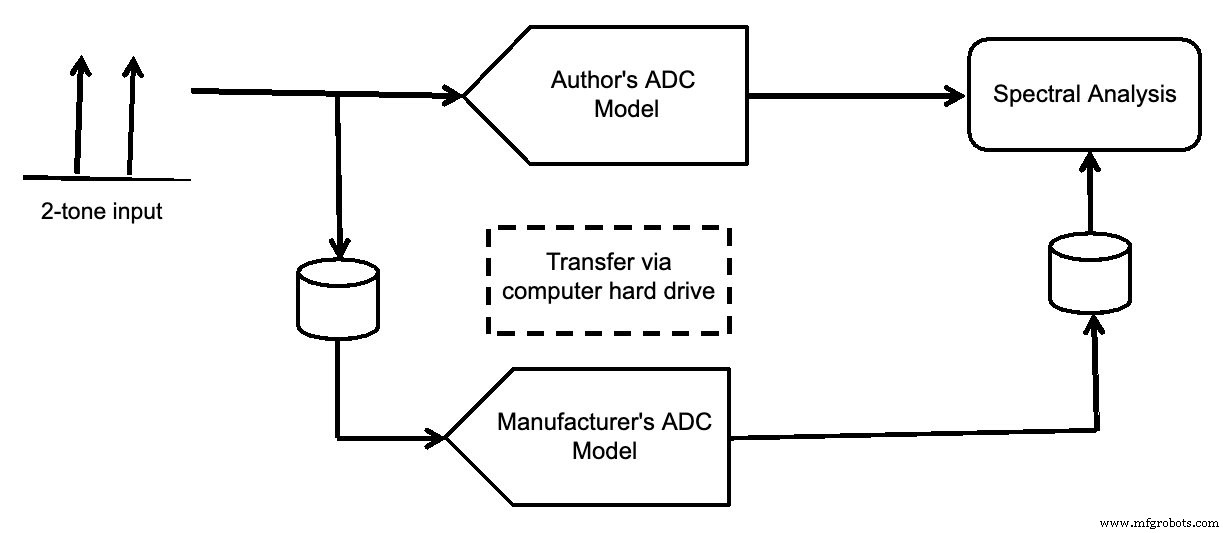
Figura 7.

La figura 8 muestra la entrada utilizada. Los dos tonos están entre 300 y 350 MHz. La frecuencia de muestreo del ADC es de aproximadamente 250 MHz, por lo que estos tonos se encuentran en la tercera zona de Nyquist.

Dado que cada uno está en -6.02 dBpeakFS, cuando agregan en fase, el voltaje será el doble, lo que resultará en 0 dBpeakFS.

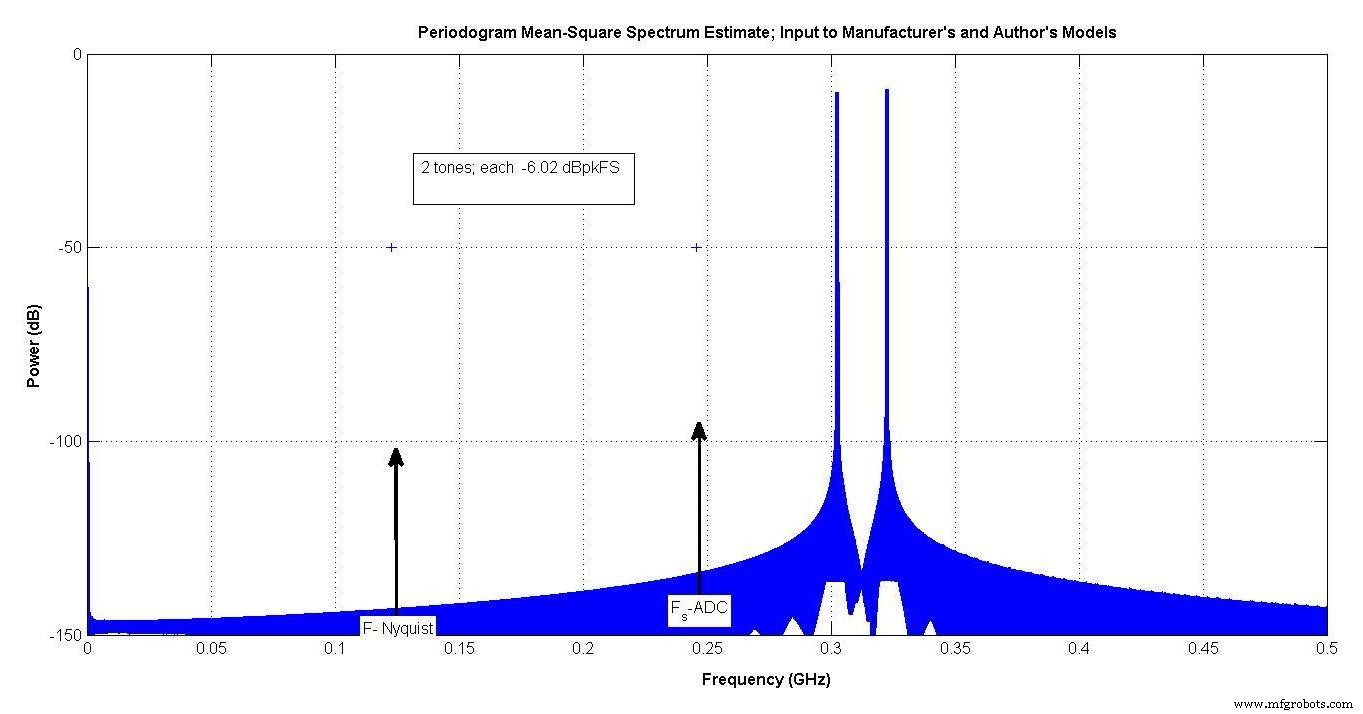
Figura 8.

La Figura 9 muestra la salida del modelo del fabricante, que tenía un SINAD de 63,74 dB en el "ancho de banda interesante" de aproximadamente 27 a 107 MHz.

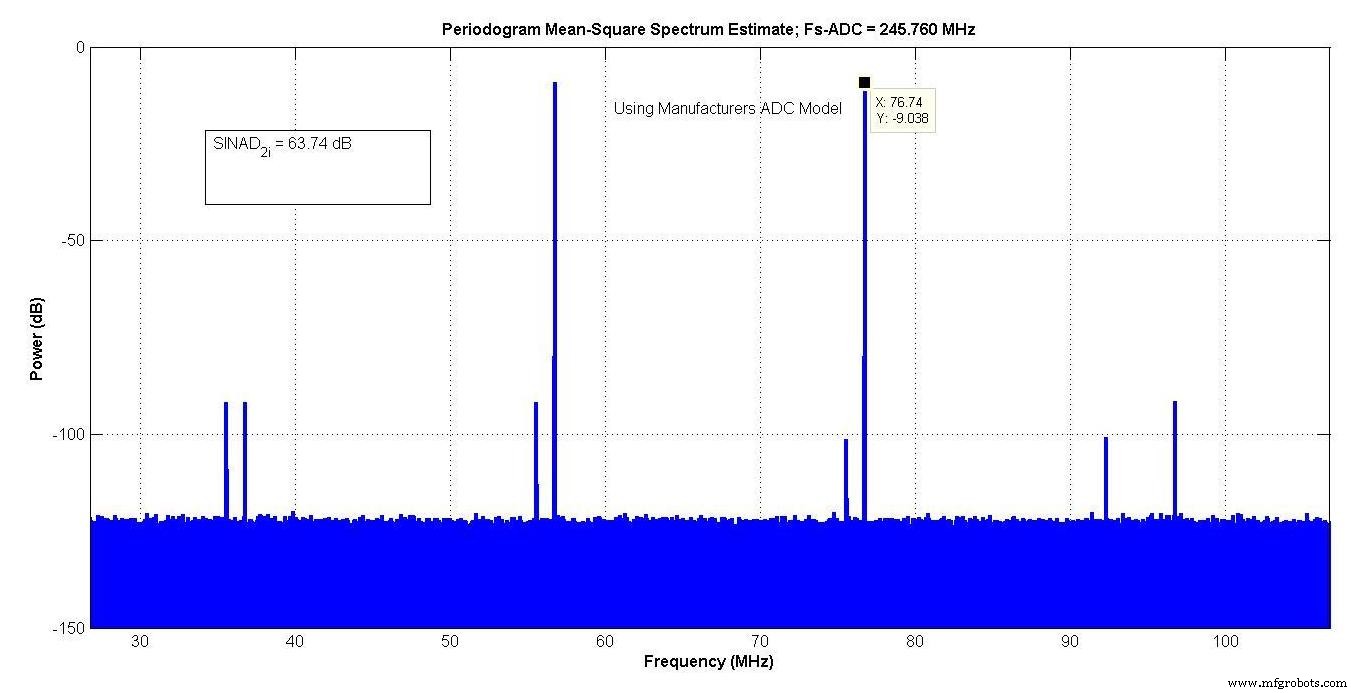
Figura 9.

La Figura 10 muestra el resultado después de ajustar los parámetros del modelo de su autor para una coincidencia.

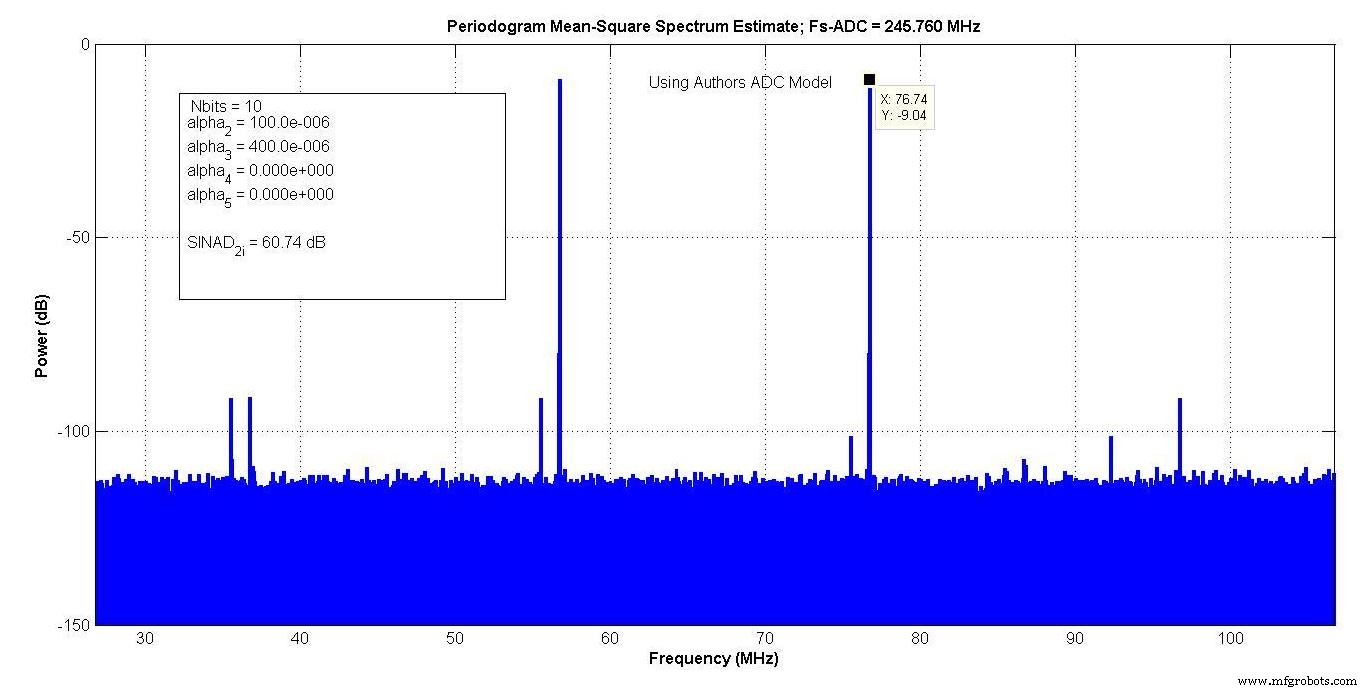
Figura 10.

Los coeficientes polinomiales dieron suficientes grados de libertad para que se pudiera hacer una coincidencia casi exacta con las espuelas. N _E de 11 bits dio un piso de ruido 3 dB por debajo del modelo del fabricante, y N _E de 10 bits le dio 3 dB por encima del modelo del fabricante.

Su autor decidió utilizar el valor pesimista de 10 bits, lo que dio un SINAD de 60,74 dB. Un modelo mejorado permitiría agregar hasta 6 dB de ruido gaussiano blanco aditivo, por lo que el valor más alto de N _E podría elegirse, y el ruido adicional se agregó para que coincida con los pisos de ruido.

Entrada de forma de onda OFDM

Los dos modelos ahora se pueden comparar con una forma de onda de comunicaciones como entrada.

Un paquete de software disponible comercialmente viene con un modelo LTE; que genera una señal OFDM. El modelo incluye un modulador, un canal de desvanecimiento Rayleigh selectivo en frecuencia, ruido gaussiano blanco aditivo y un demodulador.

Es posible insertar los modelos ADC frente al demodulador y evaluar el espectro de la salida ADC y la magnitud del vector de error de la señal OFDM, como se muestra en la Figura 11.

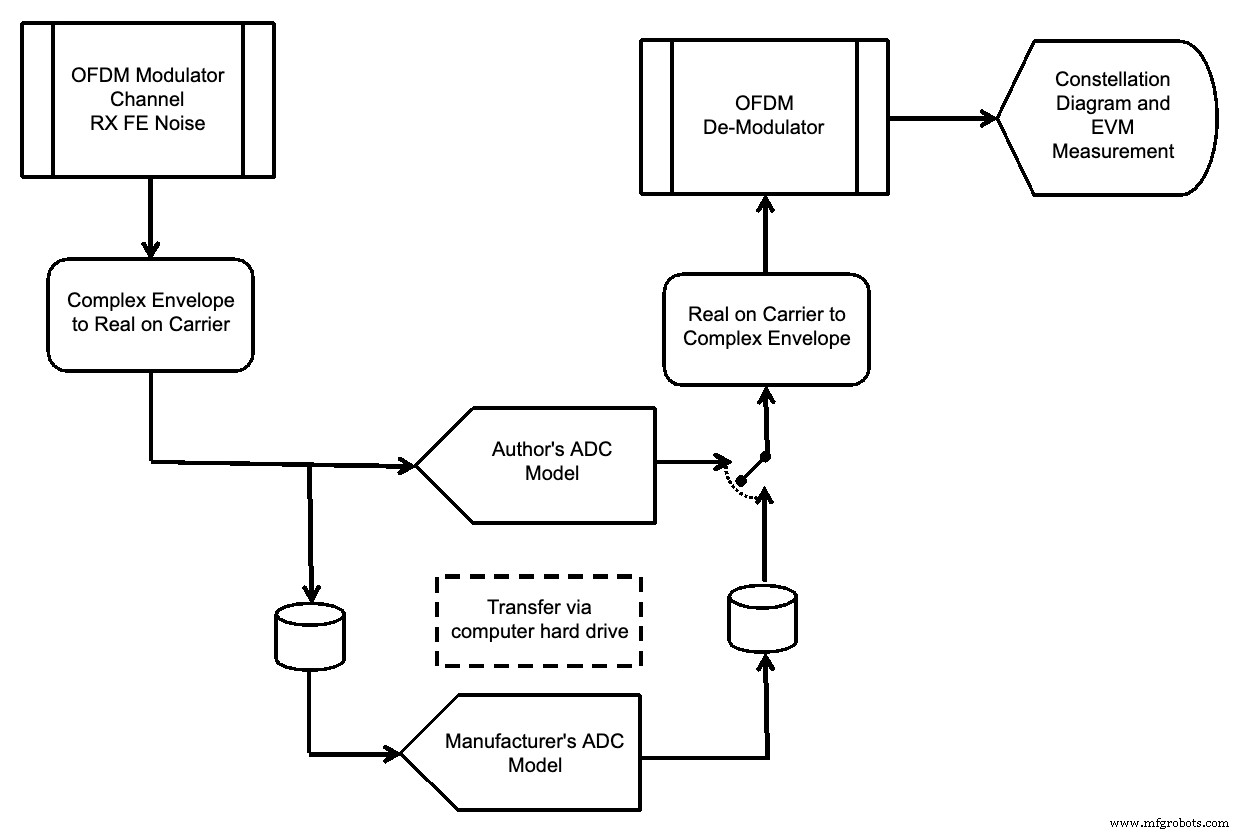
Figura 11.

Se utilizó una señal OFDM que tenía subportadoras 64-QAM. Los parámetros del modelo ADC de su autor son los mismos que los utilizados en la Figura 10.

El paquete de software disponible comercialmente utiliza una notación envolvente compleja [3] para formar sus señales. Esto permite que solo la información de modulación sea rastreada muestra a muestra por números complejos, y la frecuencia de la portadora simplemente se mantenga como una constante conocida. Por lo tanto, la cantidad de muestras necesarias para describir la forma de onda se reduce considerablemente.

Sin embargo, las entradas a los modelos ADC deben ser una señal real en una portadora explícita, para tener en cuenta la diferencia en el rendimiento del ADC en función de la frecuencia de entrada. Por lo tanto, era necesario realizar las transformaciones de "Envolvente complejo a Real en el portador" y "Real en el portador a envolvente complejo" [3].

La Figura 12 muestra la entrada de señal OFDM a ambos modelos de ADC. Está centrado en la misma frecuencia que los dos tonos que se muestran en la Figura 8.

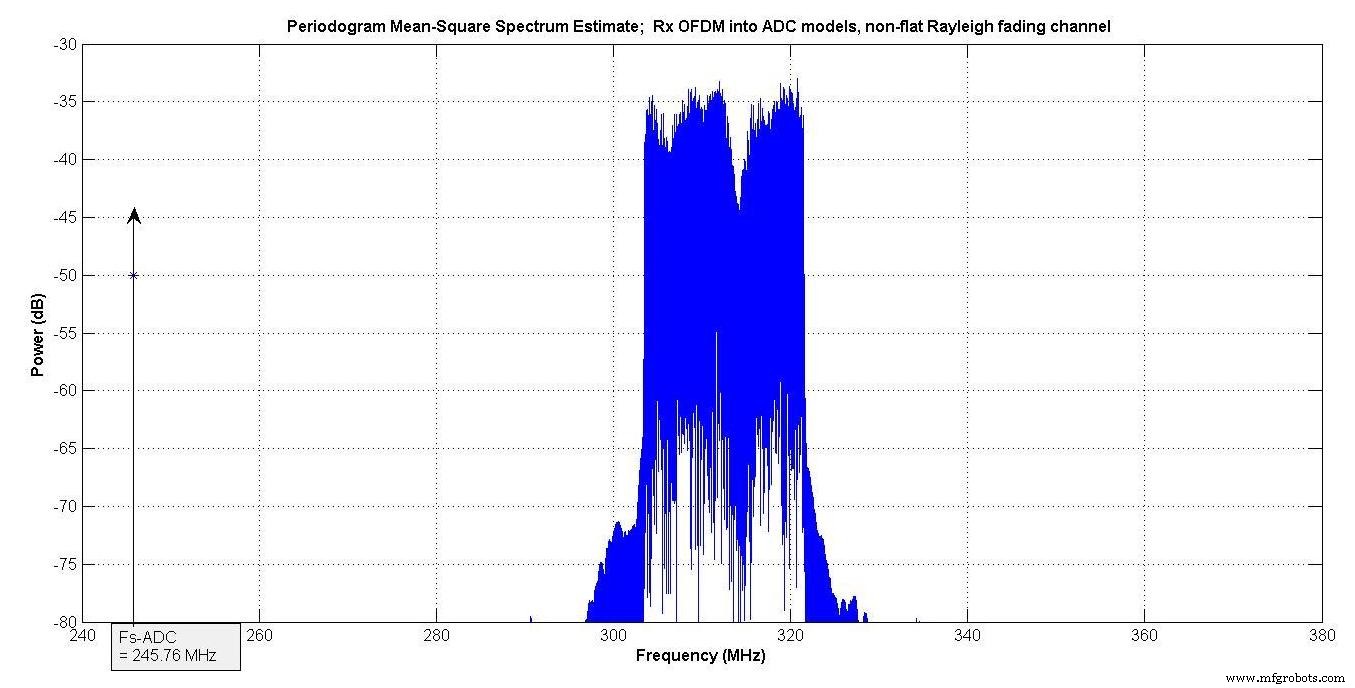
Figura 12.

El nivel dBrmsFS en ambos modelos ADC fue -7 dBrmsFS.

La Figura 13 muestra el espectro del modelo del fabricante y la Figura 14 el del modelo de su autor. Ambos muestran un recrecimiento espectral debido a la no linealidad de los ADC. Los espectros están muy cerca.

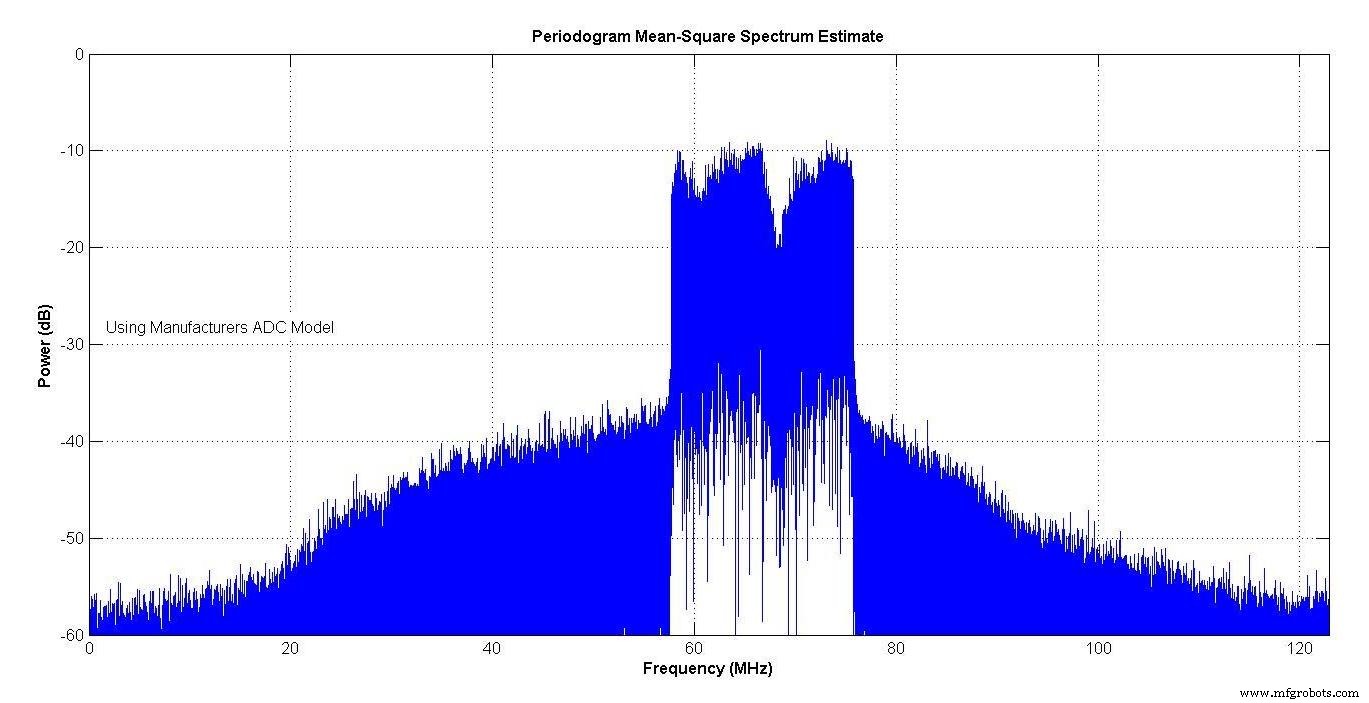
Figura 13.

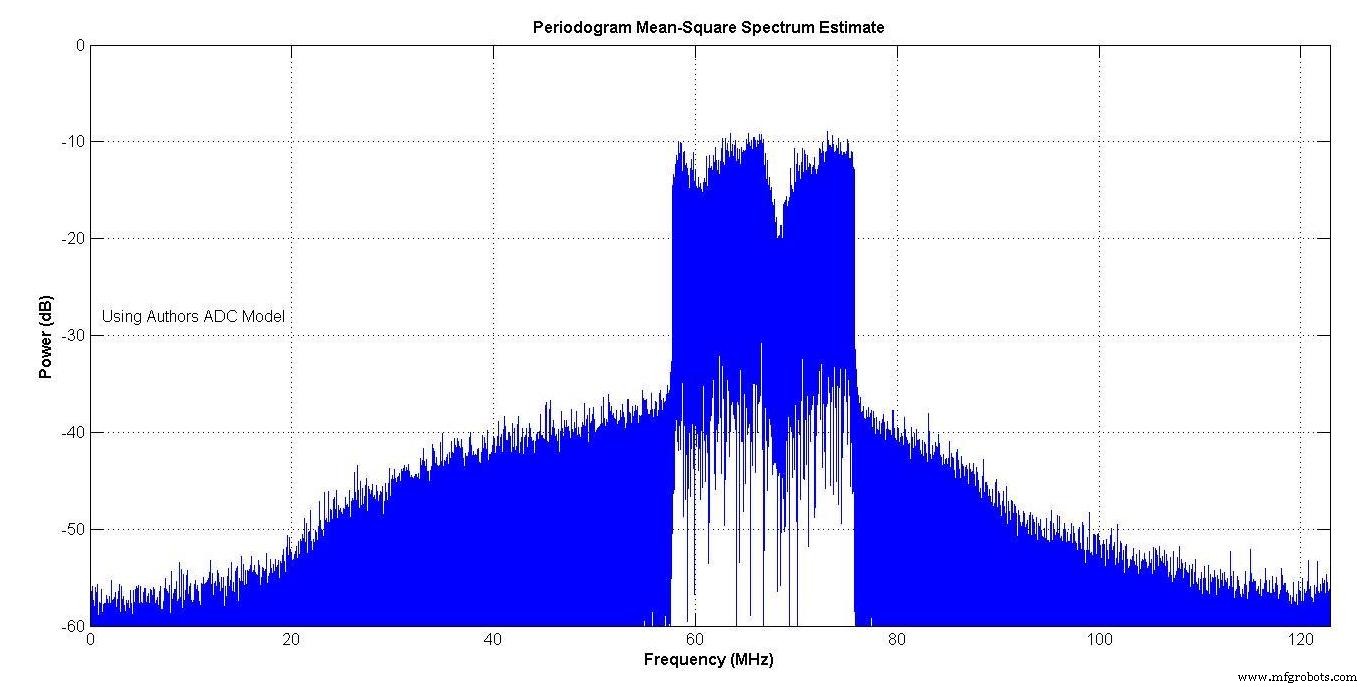
Figura 14.

La Figura 15 muestra la constelación del OFDM recibido para el modelo del fabricante y la Figura 16 lo muestra para el modelo de su autor.

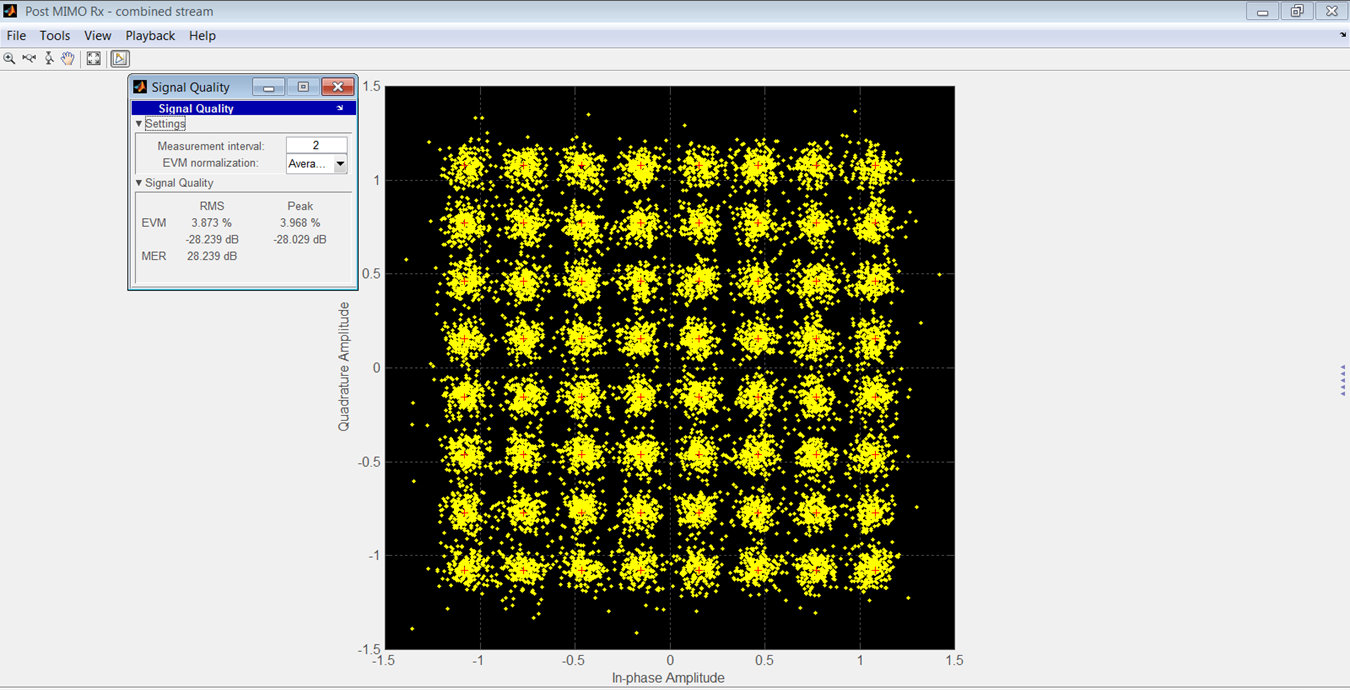
Figura 15.

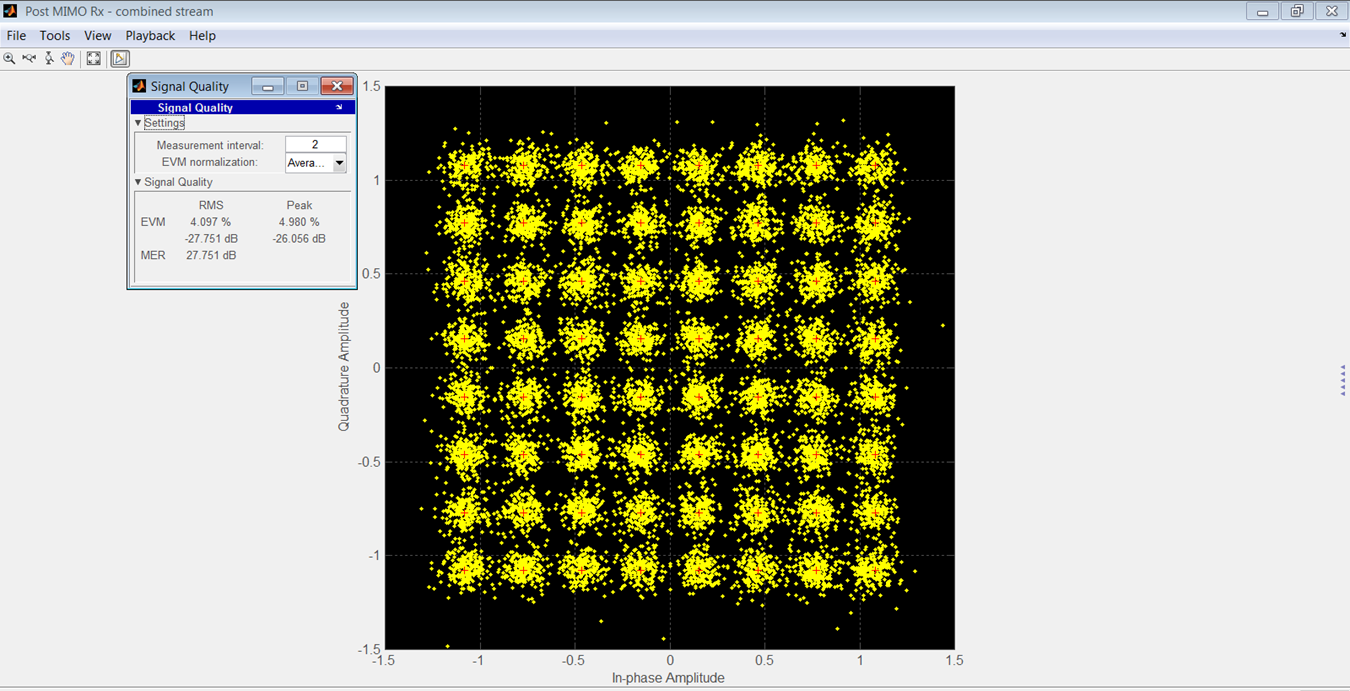
Figura 16.

En la Tabla 3 se muestra una comparación de rms y EVM pico. La SNR fue de 90 dB para estos resultados.

Tabla 3.

En un rango de -7 a -47 dBrmsFS, la diferencia rms entre los EVM de los dos modelos fue de 3,46 dB.

En general, el modelo de su autor da resultados muy similares a los del fabricante, para un conjunto de parámetros bastante simple. No había información disponible sobre el modelo del fabricante, pero puede ser similar al de su autor.

En cualquier caso, las simulaciones se ejecutaron más rápido cuando se utilizó el modelo de su autor, porque no era necesario transferir datos entre el software de simulación. Entonces, el modelo de su autor se usó en la simulación de tasa de error de bits (BER) que se muestra en la Figura 17.

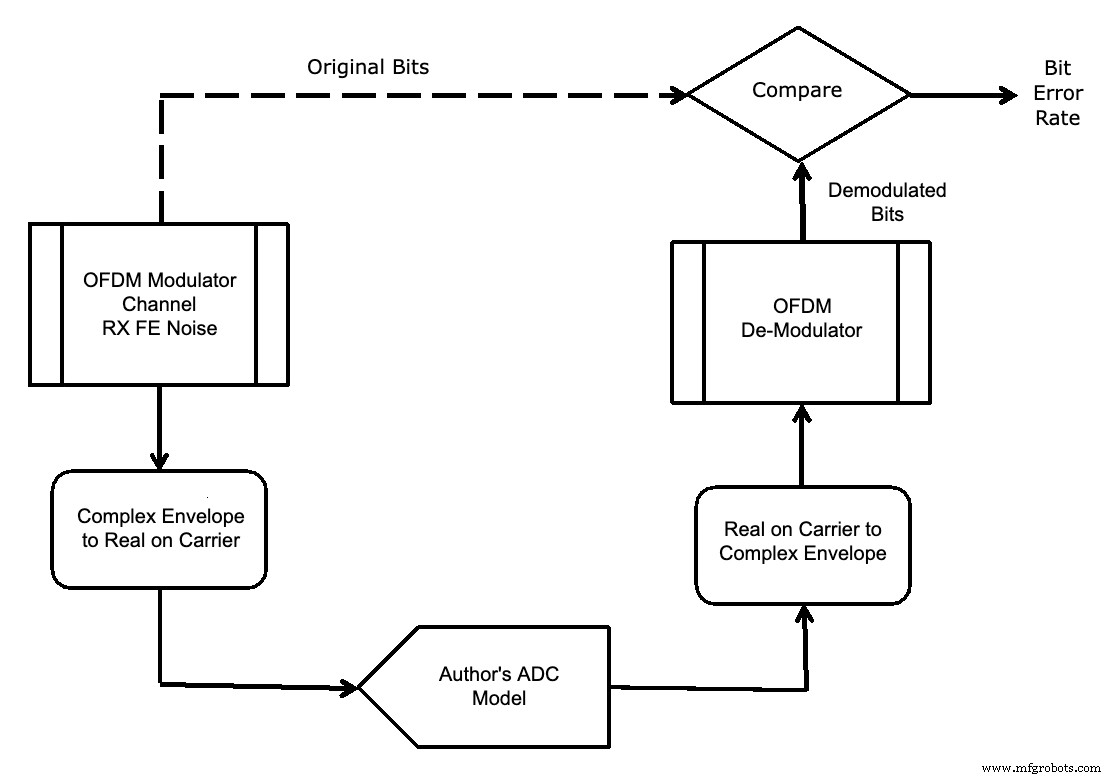
Figura 17.

Un parámetro importante al diseñar un sistema con un ADC es el nivel óptimo para colocar la señal en relación con la escala completa del ADC.

Un nivel demasiado bajo hace que la señal sea demasiado pequeña en relación con el ruido y la distorsión.

Un nivel demasiado alto da como resultado un recorte excesivo, que también distorsiona la señal. Por lo general, un nivel que permite cierto recorte es óptimo.

La BER para tres SNR diferentes y niveles de señal de -41 a -7 dBrmsFS se muestra en la Figura 18.

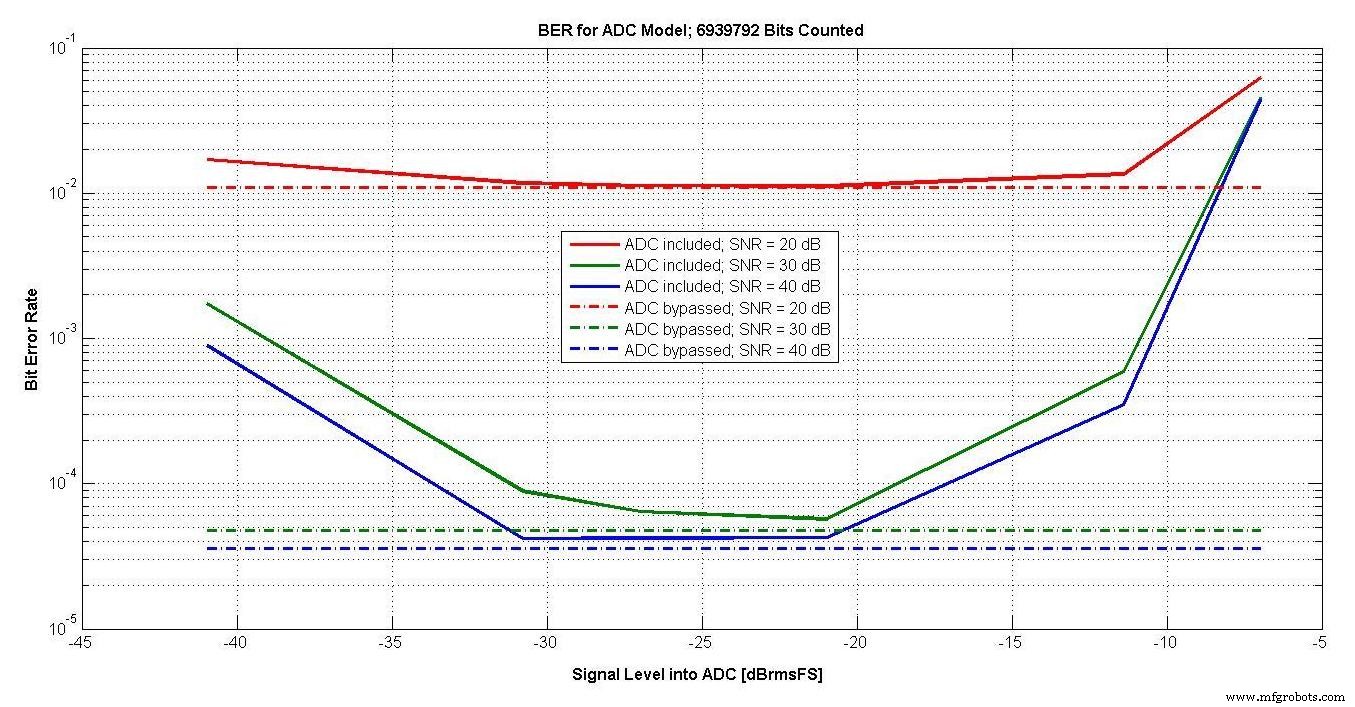
Figura 18.

También se muestra con líneas discontinuas la BER cuando se omite el modelo ADC. Con el ADC, hay aproximadamente un rango de 10 dB que es óptimo, y un control automático de ganancia debería mantener la señal en este rango.

En el próximo artículo, terminaremos esta serie concluyendo con algunas ideas sobre un mejor modelo para usar y también hablaremos un poco sobre modelos para DAC. Comparta sus pensamientos sobre esta serie en los comentarios a continuación.

¿Cuál es el espectro de potencia del ruido de cuantificación? ¿Cómo se deben modelar los convertidores de datos para las simulaciones del sistema?