Cálculo de transformadas rápidas de Fourier en la MCU LPC55S69

Este artículo investiga el motor de transformación, otra parte del PowerQuad, que permite al MCU LPC55S69 calcular una transformación rápida de Fourier (FFT).

El microcontrolador LPC55S69 de NXP contiene muchas características que lo hacen adecuado para una variedad de aplicaciones. El MCU LPC55S69 y su unidad PowerQuad incluyen componentes únicos, Biquad y Transform Engines, que se utilizan para completar varias tareas, dejando los núcleos de la CPU principal libres para otras cosas.

Un artículo anterior, Comprensión del filtrado digital con microcontroladores integrados, exploró varios métodos ampliamente utilizados para filtrar y procesar muestras de datos en el dominio del tiempo. Para eso, utilizó el motor Biquad de la unidad PowerQuad del LPC55S69.

Este artículo investiga el motor de transformación, otra parte del PowerQuad, que permite que la MCU LPC55S69 calcule una transformación rápida de Fourier (FFT).

Comprensión de las transformadas discretas de Fourier

Cuando se trata de medidas cotidianas, como longitudes y temperaturas, existe un conjunto de herramientas para determinar el tamaño y la temperatura de la cosa en particular que se está midiendo. Para las señales en el dominio del tiempo, la elección de la herramienta de medición puede no ser tan evidente. Considere el siguiente ejemplo de señal que se muestra en la Figura 1.

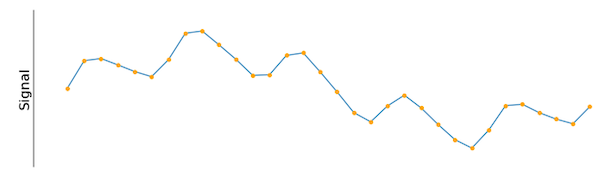
Figura 1. Una señal de entrada muestreada a un intervalo constante.

¿Cómo se puede medir, comprender y describir esta señal? Las opciones posibles podrían ser la amplitud, la frecuencia o varios valores calculados con métodos de estadística. Una forma de comenzar es comparando la señal de interés con una onda cosenoidal conocida, que se muestra en la Figura 2.

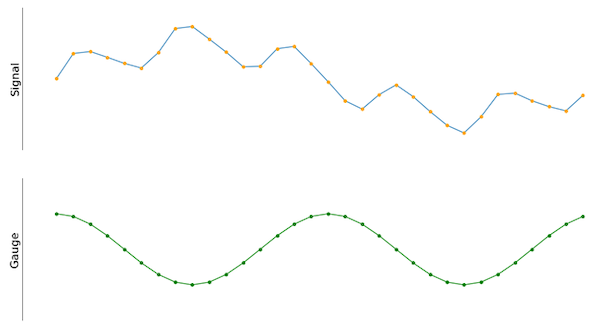
Figura 2. La señal de entrada junto a una señal de indicador de coseno. Ambos tienen la misma cantidad de muestras.

Debido a que la amplitud y la frecuencia de la onda del coseno se pueden fijar fácilmente y, por lo tanto, identificarla, es posible comparar la onda del coseno con la señal de entrada. Si se hace correctamente, el valor resultante del producto punto entre la señal de entrada y la onda del coseno cuantifica cuánto se correlaciona la señal de entrada con el medidor. Por eso, es razonable pensar en la entrada y la señal de calibre como matrices de entrada discretas de la misma longitud, y resulta fácil calcular el producto escalar.

El resultado es un escalar, y su magnitud es proporcional a qué tan bien se correlaciona la señal de entrada con la señal del medidor de coseno. La operación del producto punto se reduce a muchas operaciones de multiplicar y sumar, la misma operación que se describe en Comprensión del filtrado digital con microcontroladores integrados.

Este método da buenos resultados rápidamente. Sin embargo, hay un caso particular que no funciona al aplicar este método. Si la señal de entrada es una onda de coseno con la misma frecuencia que el medidor, pero con su fase desplazada 90 grados con respecto al medidor, la salida del método mencionado anteriormente será cero. Por inspección visual, parece que todavía existe una correlación entre el medidor y la señal de entrada, pero hay detalles que debemos tener en cuenta.

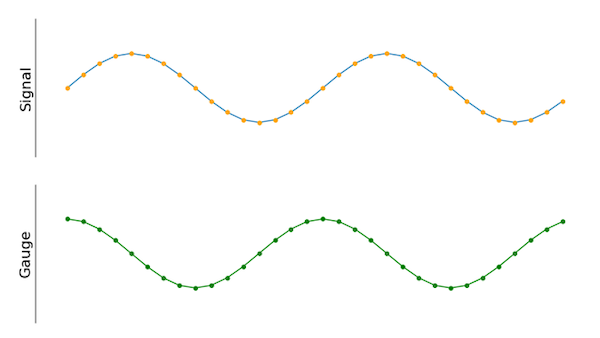
Figura 3. La nueva señal del medidor tiene un desfase de 90 grados en comparación con la anterior.

Este comportamiento podría compararse con la medición de la "longitud" de una tira fina de papel. Cuando use una regla para determinar la longitud de un lado de la tira de papel, el papel puede tener 10 pulgadas de largo y una pulgada de ancho. Ambos números son correctos, pero la regla tuvo que rotarse 90 grados para obtener ambas medidas. Ambos números son técnicamente correctos y podemos usarlos juntos para obtener un verdadero "tamaño" (largo y ancho) de nuestra hoja de papel. Para superar este problema en términos de nuestra señal de entrada, se puede usar un segundo indicador, como se ve en la Figura 4.

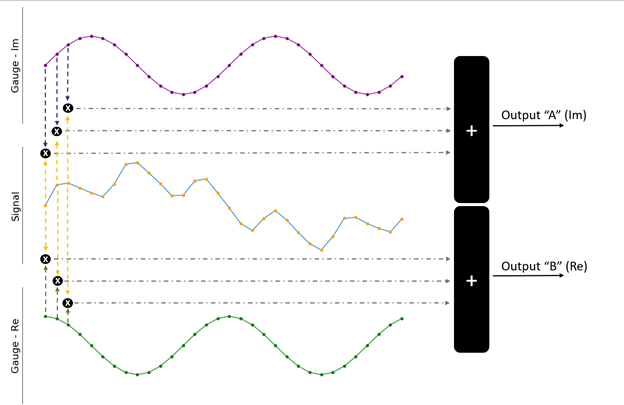
Figura 4. Ambas señales de calibre se pueden utilizar para cuantificar mejor la señal de entrada.

La única diferencia entre los dos indicadores (mostrados en violeta y verde) es el cambio de fase de 90 grados. En la analogía anterior, esto equivale a rotar la regla. El producto escalar se calcula entre la señal de entrada y cada uno de los medidores para obtener la salida final. Esto da como resultado dos valores A y B, cada uno de los cuales contiene qué tan bien se correlaciona la entrada con uno de los medidores. Por lo general, se consideran como un solo número complejo:

salida =B + i * A

El siguiente paso es comparar la señal de entrada con un rango de medidores con diferentes frecuencias (Figura 5).

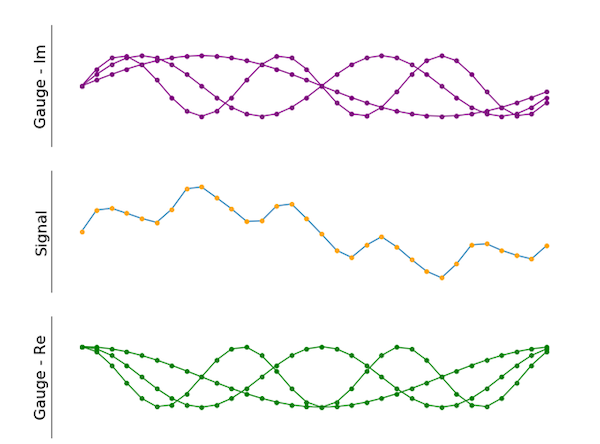
Figura 5. También se pueden aplicar varios calibres. Los verdes se desplazan 90 grados en comparación con los morados.

Como muestra la imagen, el resultado final incorpora algunos calibres diferentes. La parte imaginaria (mostrada en violeta) tiene un desfase de 90 grados en comparación con las señales verdes (parte real), al igual que en el ejemplo de dos indicadores que se muestra arriba. No hay límite para el número de calibres diferentes.

El uso de esta técnica, llamada Transformada Discreta de Fourier (DFT), produce la generación de un espectro de salidas en todas las frecuencias de interés para un problema. Es posible enunciar la técnica matemáticamente de la siguiente manera:

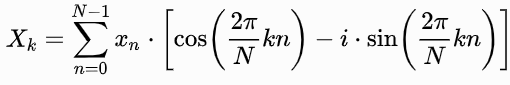
Ecuación 1. La descripción matemática de la DFT.

Donde N es el número de muestras en la señal de entrada yk es la frecuencia de los medidores de referencia (co) sinusoidales.

Limitaciones de la Transformada Rápida de Fourier (FFT)

La FFT es una forma numéricamente eficiente de calcular la DFT que requiere menos operaciones de multiplicar y sumar en comparación con el método discutido anteriormente. Sin embargo, existen algunas restricciones para la entrada:

1. La longitud de la entrada debe ser una potencia de dos.
2. No se permiten longitudes de entrada arbitrarias ni espaciado de frecuencia en la salida. Los contenedores de salida están separados por la frecuencia de muestreo de la señal de entrada dividida por el número de muestras en la entrada. Si la entrada es, por ejemplo, una señal de 256 puntos muestreada a 48 kHz, las matrices de salida corresponden a frecuencias espaciadas a 187 Hz (48.000 dividido por 256).
3. Cuando la entrada consta de números reales (por ejemplo, muestras obtenidas de un ADC), la salida es simétrica. Si la entrada, por ejemplo, consta de 64 muestras, el resultado de FFT también constará de 64 números complejos. Sin embargo, la segunda mitad de la matriz de salida contiene los conjugados complejos de la primera mitad.

Uso del motor PowerQuad FFT

Las matemáticas detrás de las operaciones DFT / FFT se pueden realizar mediante operaciones simples de multiplicar y sumar, lo cual es ideal para subcontratar las operaciones matemáticas a un coprocesador dedicado, como el PowerQuad en la MCU LPC55S69. Debido a esto, los núcleos principales de la CPU son libres para trabajar en otras tareas.

Utilizar el motor PowerQuad FFT es un proceso simple, y el SDK oficial viene con proyectos de ejemplo que demuestran las funciones de coprocesamiento. Un ejemplo en particular, llamado powerquad_transform, demuestra el proceso de cálculo de FFT.

El archivo powerquad_transform.c contiene varias funciones que prueban los diferentes modos del motor FFT. Uno de ellos es la función PQ_RFFTFixed16Example. Este ejemplo inicializa el PowerQuad para aceptar datos enteros de 16 bits. Los datos de punto flotante deben convertirse a valores de punto fijo de antemano, ya que el motor de transformación de PowerQuad solo admite números enteros.

FILTER_INPUT_LEN define el número de muestras de entrada. La matriz de salida tiene el doble de longitud porque necesita almacenar las partes real e imaginaria de los valores resultantes.

Figura 6. Esta parte del código define los datos de prueba y los resultados esperados.

La última matriz contiene datos de prueba para verificar el resultado. Observe cómo la segunda mitad de la matriz contiene los conjugados complejos como se indicó anteriormente. Además, los conjugados no son iguales (por ejemplo, el par 76, -50 y 77,49). De todos modos, una vez que se inicializaron los datos, se utiliza la siguiente estructura de datos para configurar el PowerQuad:

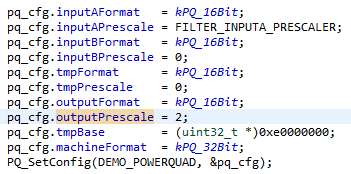
Figura 7. Esta parte del programa de ejemplo configura e inicializa la unidad PowerQuad.

Es necesario reducir la escala de la entrada para evitar que el algoritmo se desborde. Este proceso ocurre en la segunda línea de la imagen de arriba. FILTER_INPUTA_PRESCALER se establece en cinco porque hay 32 (dos elevado a cinco) muestras. El preescalado es otra característica de hardware del PowerQuad, y es probable que sea la razón de la imprecisión observada en los resultados esperados de la prueba.

Una vez que todo está configurado, la ubicación de las áreas de entrada y salida se pasa a la unidad PowerQuad, lo que ocurre en la función PQ_transformRFFT. Este método establece algunos registros de configuración e inicia el PowerQuad escribiendo en el registro de control. En este ejemplo, la CPU espera a que finalice el PowerQuad. No siempre es necesario esperar, y el PowerQuad puede realizar cálculos de forma asincrónica mientras la CPU realiza otras tareas.

Utilice PowerQuad para operaciones matemáticas

El PowerQuad es un coprocesador para operaciones matemáticas complejas disponible en varios dispositivos de la serie LPC5500 MCU. Incluye un motor especial para calcular de manera eficiente las FFT, que se puede hacer independientemente de los núcleos de la CPU principal. El SDK para la MCU LPC55S69 contiene ejemplos de cómo configurar y usar PowerQuad.

La página de la comunidad de NXP contiene amplia información, debates y artículos centrados en la MCU LPC55S69.

Los artículos de la industria son una forma de contenido que permite a los socios de la industria compartir noticias, mensajes y tecnología útiles con los lectores de All About Circuits de una manera que el contenido editorial no es adecuado. Todos los artículos de la industria están sujetos a estrictas pautas editoriales con la intención de ofrecer a los lectores noticias útiles, experiencia técnica o historias. Los puntos de vista y las opiniones expresados ​​en los artículos de la industria son los del socio y no necesariamente los de All About Circuits o sus redactores.