Decibeles

Bel se utiliza para representar la ganancia

En su forma más simple, la ganancia de un amplificador es una relación de salida sobre entrada. Como todas las proporciones, esta forma de ganancia no tiene unidades. Sin embargo, hay una unidad real destinada a representar la ganancia, y se llama bel .

Como unidad, el bel se diseñó como una forma conveniente de representar la pérdida de energía. en el cableado del sistema telefónico en lugar de ganancia en amplificadores. El nombre de la unidad se deriva de Alexander Graham Bell, el famoso inventor escocés cuyo trabajo fue fundamental en el desarrollo de sistemas telefónicos. Originalmente, el bel representaba la cantidad de pérdida de potencia de la señal debido a la resistencia en una longitud estándar de cable eléctrico. Ahora, se define en términos del logaritmo común (base 10) de una relación de potencia (potencia de salida dividida por potencia de entrada):

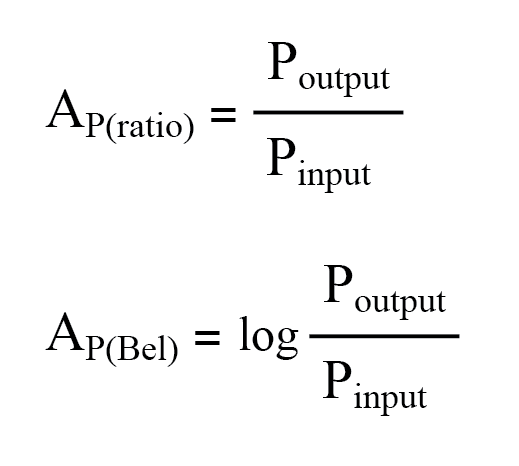
Bel no es lineal

Debido a que bel es una unidad logarítmica, no es lineal. Para darle una idea de cómo funciona esto, considere la siguiente tabla de figuras, comparando pérdidas y ganancias de energía en bels versus proporciones simples:

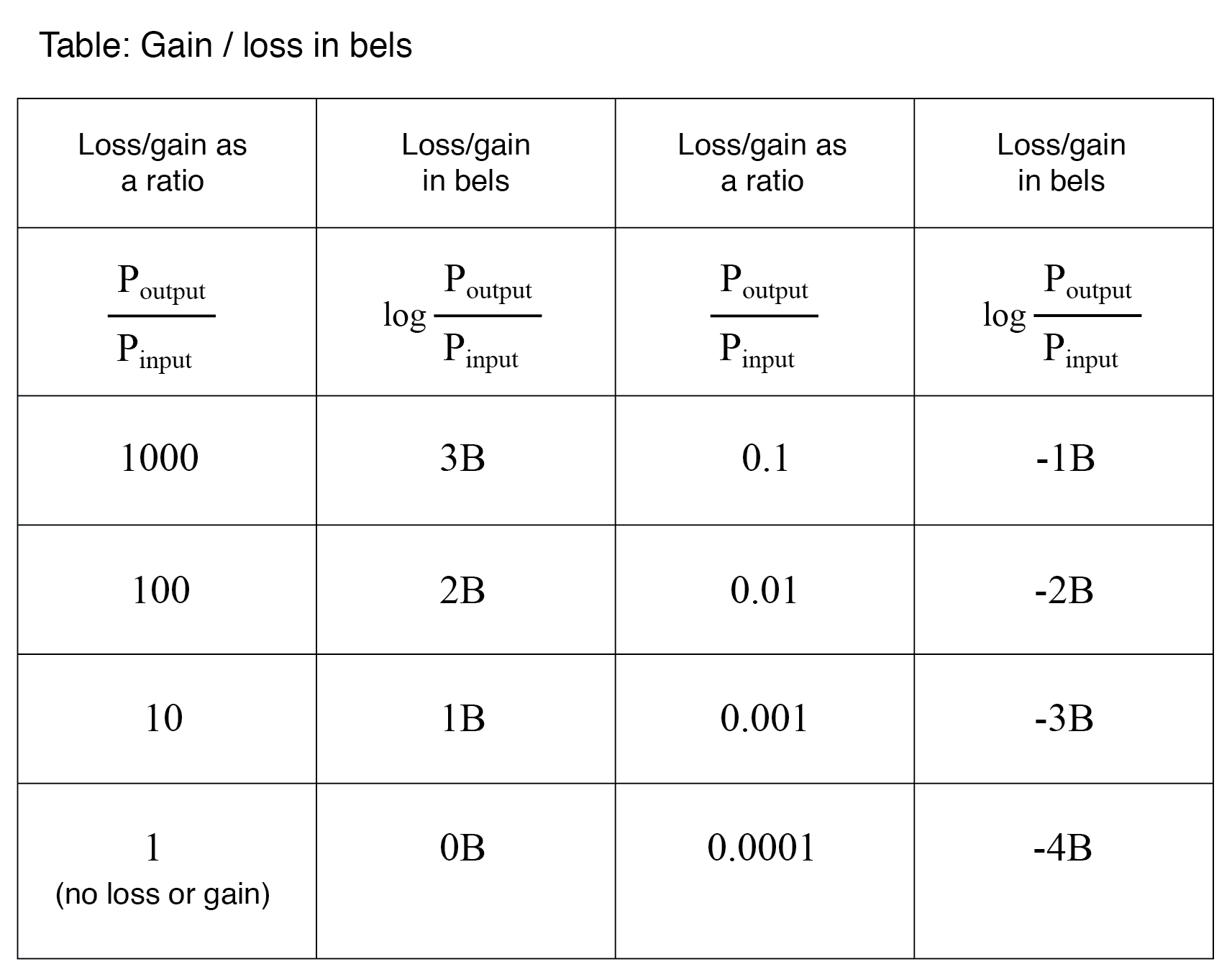
Pasar del Bel al Decibel

Más tarde se decidió que la unidad bel era demasiado grande para usarse directamente, por lo que se acostumbró aplicar el prefijo métrico deci (es decir, 1/10), por lo que es deci belios o dB. Ahora, la expresión "dB" es tan común que muchas personas no se dan cuenta de que es una combinación de "deci-" y "-bel", o que incluso existe una unidad como "bel". Para poner esto en perspectiva, aquí hay otra tabla que compara las relaciones de ganancia / pérdida de potencia con los decibeles:

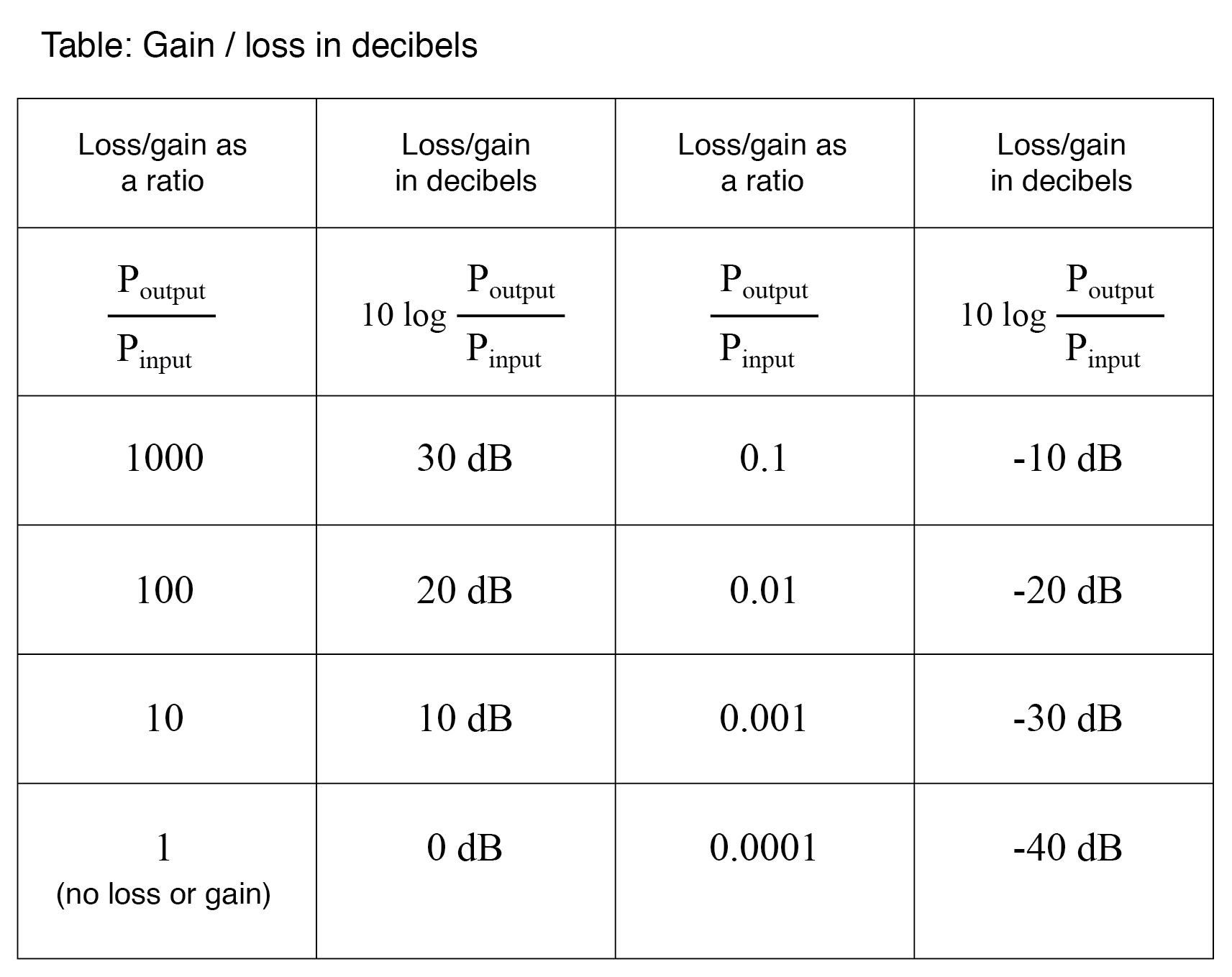
Como unidad logarítmica, este modo de expresión de ganancia de potencia cubre una amplia gama de relaciones con un intervalo mínimo de cifras. Es razonable preguntar, "¿por qué alguien sintió la necesidad de inventar un logarítmico unidad para la pérdida de potencia de la señal eléctrica en un sistema telefónico? La respuesta está relacionada con la dinámica del oído humano, cuya intensidad perceptiva es de naturaleza logarítmica.

La audición humana no es lineal

La audición humana es muy no lineal:para duplicar la intensidad percibida de un sonido, la potencia del sonido real debe multiplicarse por un factor de diez. Relacionar la pérdida de potencia de la señal telefónica en términos de la escala logarítmica “bel” tiene mucho sentido en este contexto:una pérdida de potencia de 1 bel se traduce en una pérdida de sonido percibida del 50 por ciento, o 1/2. Una ganancia de potencia de 1 bel se traduce en una duplicación de la intensidad percibida del sonido.

Otros ejemplos de escala logarítmica:escala de Richter y pH químico

Escala de Richter

Una analogía casi perfecta con la escala bel es la escala de Richter utilizada para describir la intensidad del terremoto:un terremoto de 6.0 Richter es 10 veces más poderoso que un terremoto de 5.0 Richter; un terremoto de 7.0 Richter 100 veces más poderoso que un terremoto de 5.0 Richter; un terremoto de 4.0 Richter es 1/10 más poderoso que un terremoto de 5.0 Richter, y así sucesivamente.

pH químico

La escala de medición del pH químico es igualmente logarítmica, una diferencia de 1 en la escala equivale a una diferencia de diez veces en la concentración de iones de hidrógeno de una solución química. Una ventaja de usar una escala de medición logarítmica es el enorme rango de expresión que ofrece un intervalo relativamente pequeño de valores numéricos, y es esta ventaja la que asegura el uso de números de Richter para terremotos y pH para actividad de iones de hidrógeno.

Uso de Bel para expresar las ganancias y pérdidas del sistema

Otra razón para la adopción de bel como unidad de ganancia es la simple expresión de ganancias y pérdidas del sistema. Considere el último ejemplo de sistema (figura anterior) donde se conectaron dos amplificadores en tándem para amplificar una señal. La ganancia respectiva para cada amplificador se expresó como una proporción, y la ganancia general para el sistema fue el producto (multiplicación) de esas dos proporciones:

 Ganancia general =(3) (5) =15 

Si estas cifras representaban poder ganancias, podríamos aplicar directamente la unidad de bels a la tarea de representar la ganancia de cada amplificador, y del sistema en su conjunto. (Figura siguiente)

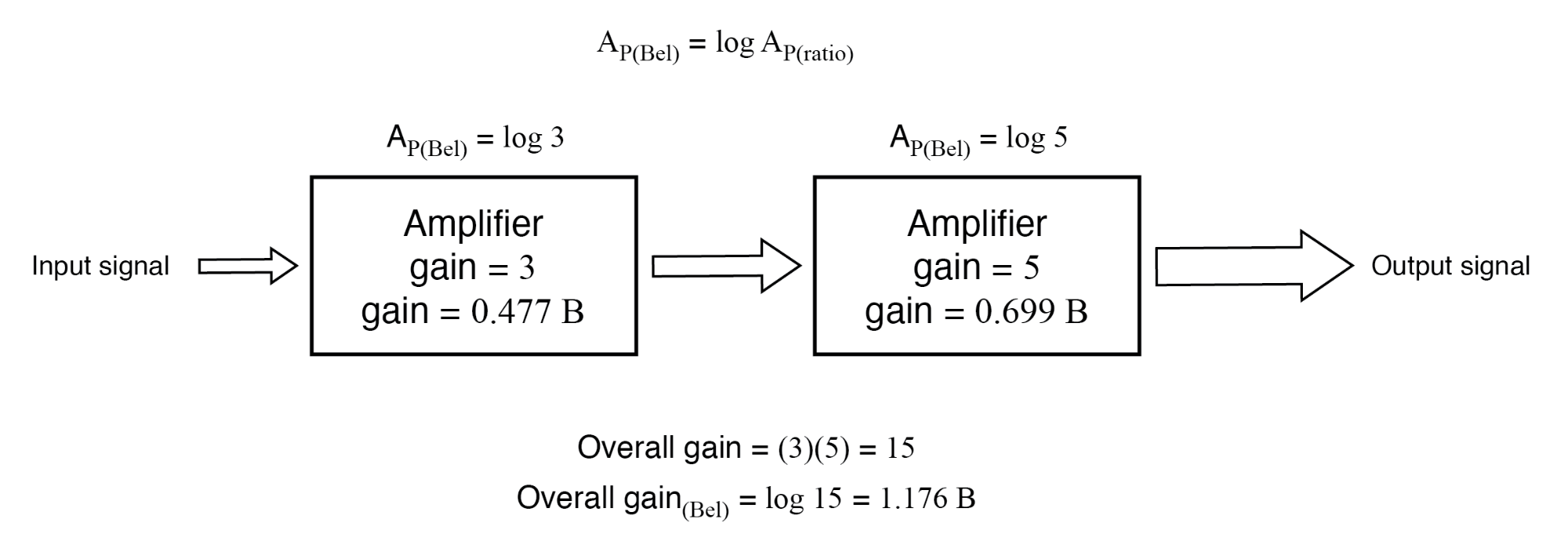
La ganancia de potencia en belios es aditiva:0,477 B + 0,699 B =1,176 B.

Una inspección minuciosa de estas cifras de ganancia en la unidad de "bel" arroja un descubrimiento:son aditivas. Las cifras de ganancia de relación son multiplicativas para amplificadores por etapas, pero las ganancias expresadas en bels suman en lugar de multiplicar para igualar la ganancia general del sistema. El primer amplificador con su ganancia de potencia de 0.477 B se suma a la ganancia de potencia del segundo amplificador de 0.699 B para hacer un sistema con una ganancia de potencia general de 1.176 B.

Ganancias usando decibelios

Al volver a calcular decibelios en lugar de belios, notamos el mismo fenómeno. (Figura siguiente)

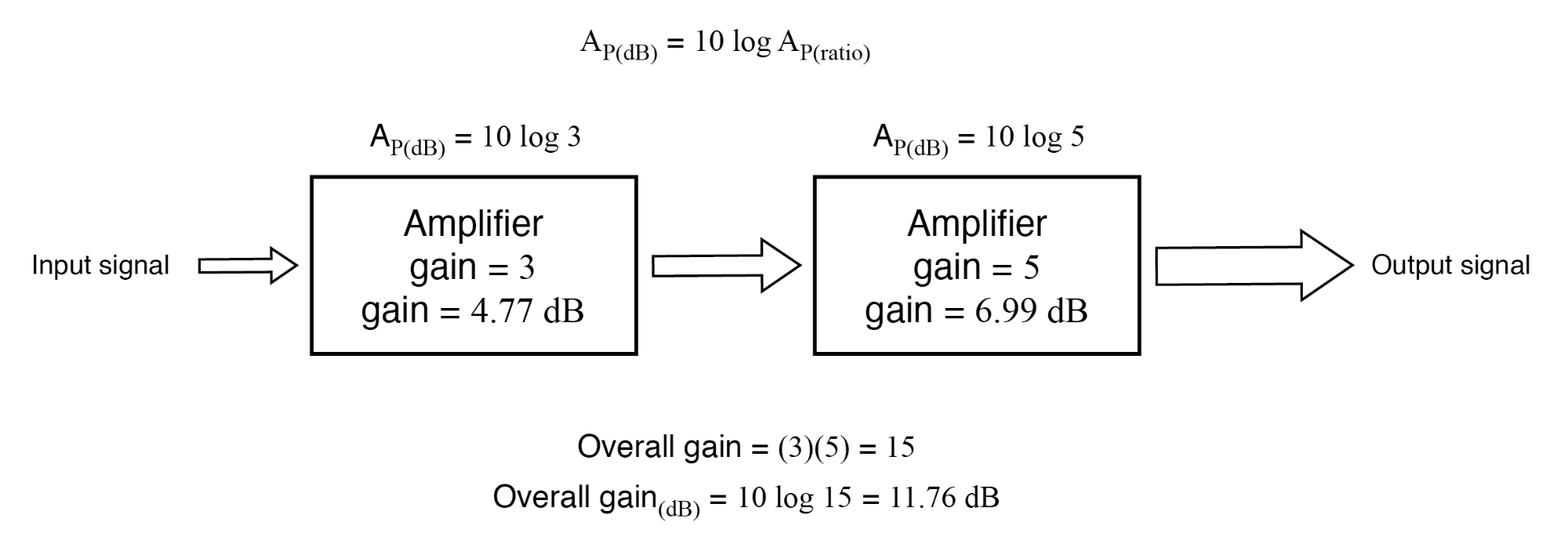
La ganancia de las etapas del amplificador en decibelios es aditiva:4,77 dB + 6,99 dB =11,76 dB.

Para aquellos que ya están familiarizados con las propiedades aritméticas de los logaritmos, esto no es ninguna sorpresa. Es una regla elemental del álgebra que el antilogaritmo de la suma de los valores del logaritmo de dos números es igual al producto de los dos números originales. En otras palabras, si tomamos dos números y determinamos el logaritmo de cada uno, luego sumamos esas dos cifras de logaritmo, luego determinamos el "antilogaritmo" de esa suma (eleva el número base del logaritmo, en este caso, 10, al potencia de esa suma), el resultado será el mismo que si simplemente hubiéramos multiplicado los dos números originales.

Esta regla algebraica forma el corazón de un dispositivo llamado regla de cálculo , una computadora analógica que podría, entre otras cosas, determinar los productos y cocientes de números mediante la suma (sumando las longitudes físicas marcadas en escalas deslizantes de madera, metal o plástico).

Dada una tabla de cifras de logaritmos, el mismo truco matemático podría usarse para realizar multiplicaciones y divisiones complejas con solo hacer sumas y restas, respectivamente. Con el advenimiento de los dispositivos de calculadora digital de mano de alta velocidad, esta elegante técnica de cálculo prácticamente desapareció del uso popular. Sin embargo, aún es importante comprender cuando se trabaja con escalas de medición que son de naturaleza logarítmica, como las escalas bel (decibelios) y Richter.

Conversión de decibeles y proporción sin unidades

Al convertir una ganancia de potencia de unidades de belios o decibelios a una relación sin unidades, se utiliza la función matemática inversa de los logaritmos comunes:potencias de 10 o el antilog .

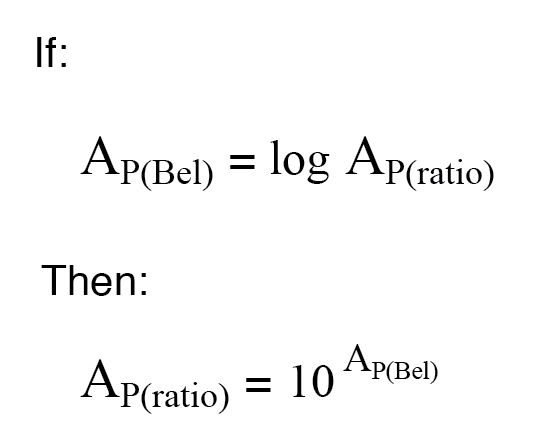
Convertir decibeles en proporciones sin unidades para la ganancia de potencia es muy similar, solo se incluye un factor de división de 10 en el término del exponente:

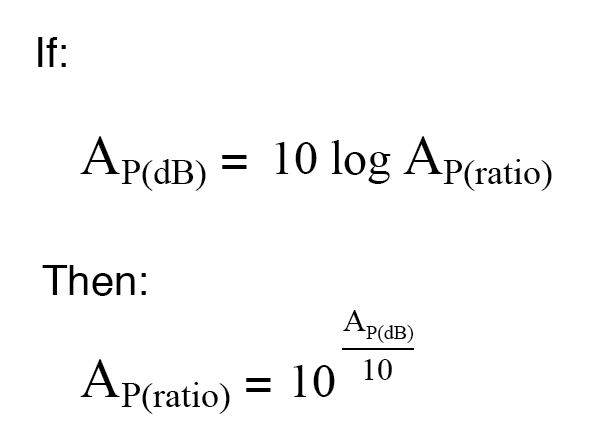
Ejemplo: La potencia de un amplificador es de 1 vatio, la potencia de salida es de 10 vatios. Encuentre la ganancia de potencia en dB.

 AP (dB) =10 * log10 (PO / PI) =10 * log10 (10/1) =10 * log10 (10) =10 * (1) =10 dB 

Ejemplo: Encuentre la relación de ganancia de potencia AP (relación) =(PO / PI) para una ganancia de potencia de 20 dB.

 AP (dB) =20 =10 * log10 (AP  relación  ) 20/10 =log10 * (AP  ratio  ) 10 ^ (20/10) =10 ^ (log10 * (AP  ratio  )) 10 ^ 2 =100 =AP (proporción) =(PO / PI) 

Conversión de la ganancia de potencia en voltaje / ganancia de corriente

Porque el bel es fundamentalmente una unidad de poder ganancia o pérdida en un sistema, las ganancias y pérdidas de voltaje o corriente no se convierten en belios o dB de la misma manera. Al usar belios o decibelios para expresar una ganancia distinta de la potencia, ya sea voltaje o corriente, debemos realizar el cálculo en términos de cuánta ganancia de potencia habría para esa cantidad de voltaje o ganancia de corriente.

Para una impedancia de carga constante, una ganancia de voltaje o corriente de 2 equivale a una ganancia de potencia de 4 (2 ² ); una ganancia de voltaje o corriente de 3 equivale a una ganancia de potencia de 9 (3 ² ). Si multiplicamos el voltaje o la corriente por un factor dado, entonces la ganancia de potencia incurrida por esa multiplicación será el cuadrado de ese factor. Esto se relaciona con las formas de la Ley de Joule donde la potencia se calculó a partir del voltaje o la corriente y la resistencia:

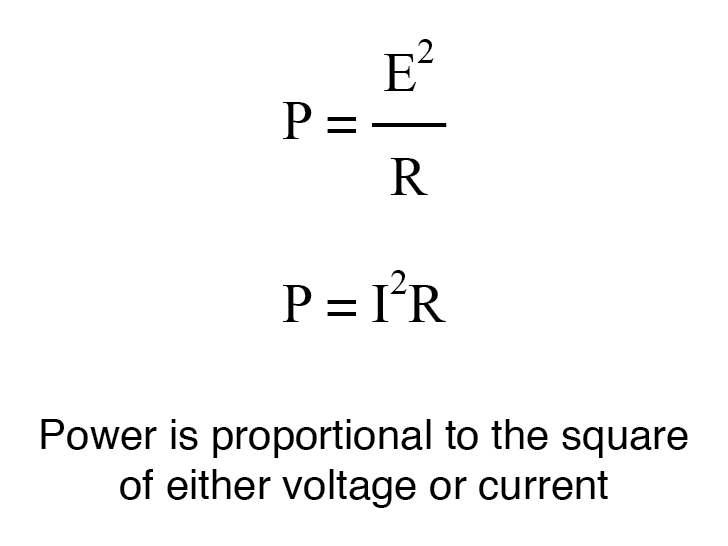
Por lo tanto, al traducir una relación de ganancia de voltaje o corriente en una ganancia respectiva en términos de la unidad bel, debemos incluir este exponente en la ecuación (es):

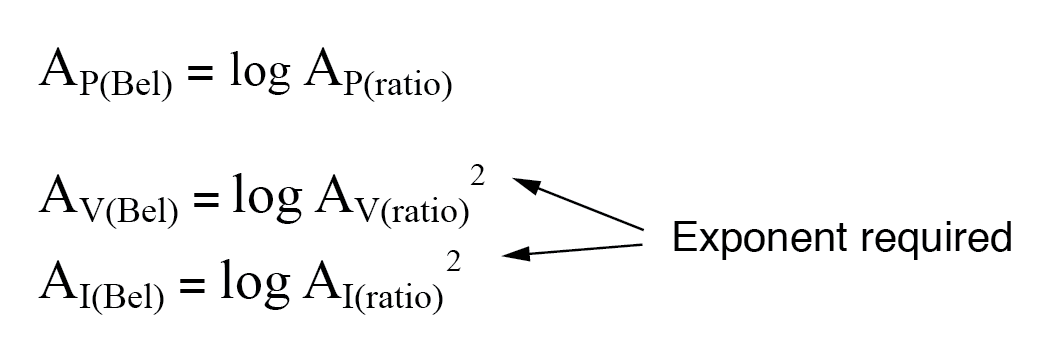
El mismo requisito de exponente se cumple cuando se expresan ganancias de voltaje o corriente en términos de decibelios:

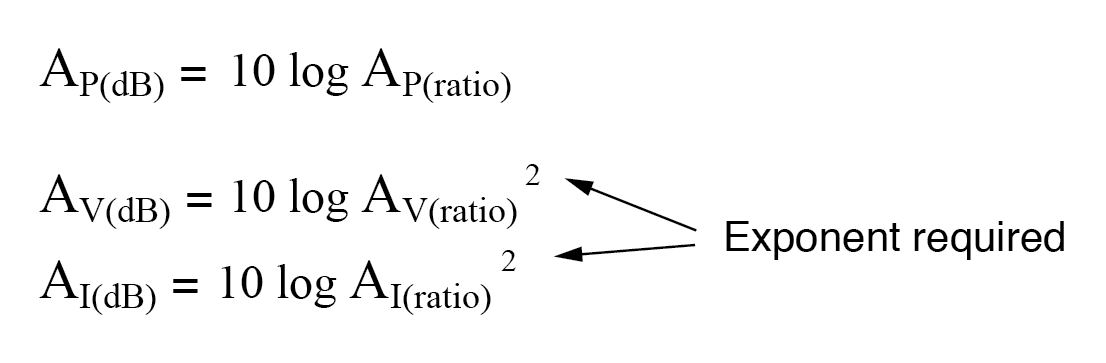
Sin embargo, gracias a otra propiedad interesante de los logaritmos, podemos simplificar estas ecuaciones para eliminar el exponente incluyendo el "2" como factor multiplicador para la función de logaritmo. En otras palabras, en lugar de tomar el logaritmo del cuadrado de la ganancia de voltaje o corriente, simplemente multiplicamos la cifra logarítmica de la ganancia de voltaje o corriente por 2 y el resultado final en bels o decibelios será el mismo:

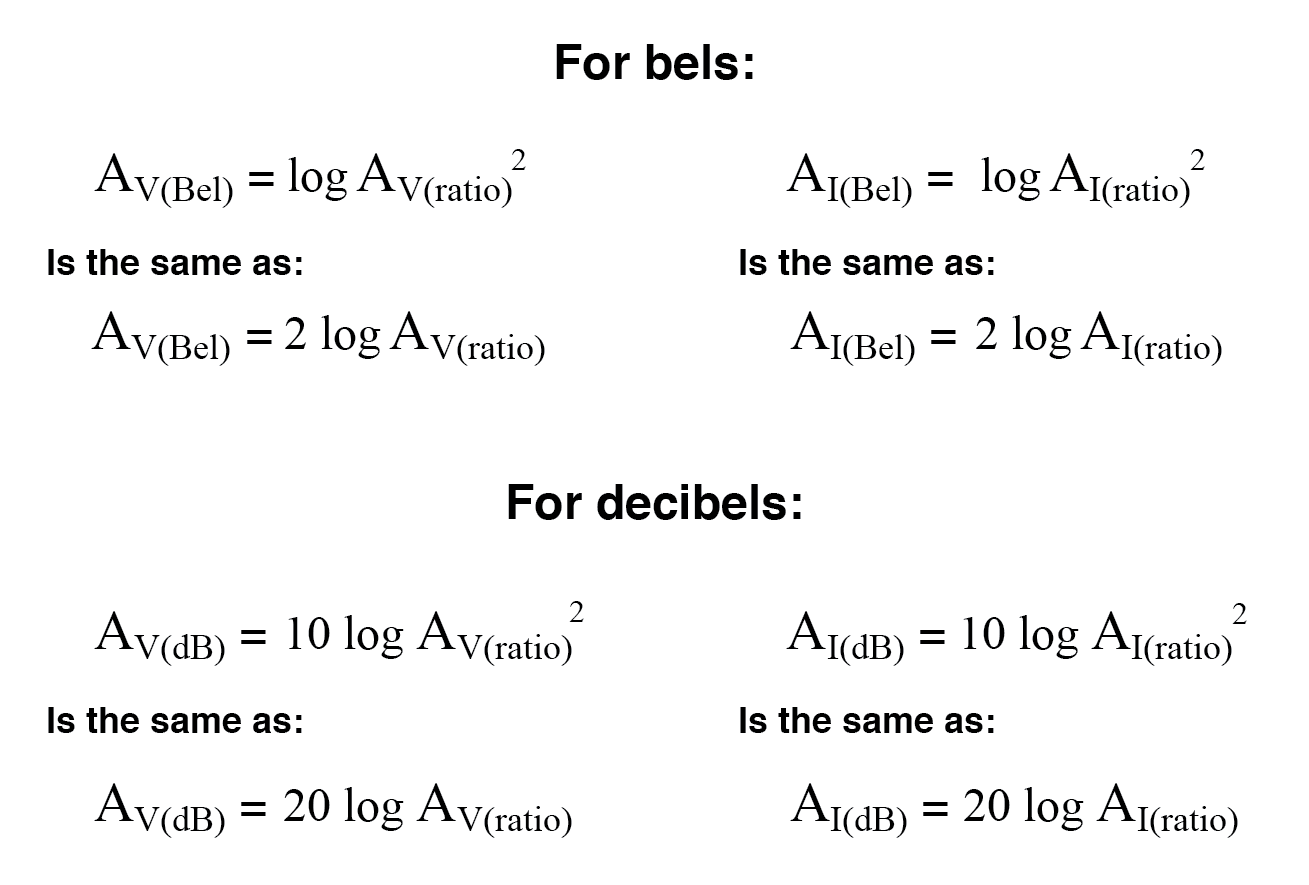
El proceso de convertir las ganancias de voltaje o corriente de bels o decibelios en relaciones sin unidades es muy similar al de las ganancias de potencia:

Estas son las ecuaciones utilizadas para convertir las ganancias de voltaje o corriente en decibelios en relaciones sin unidades:

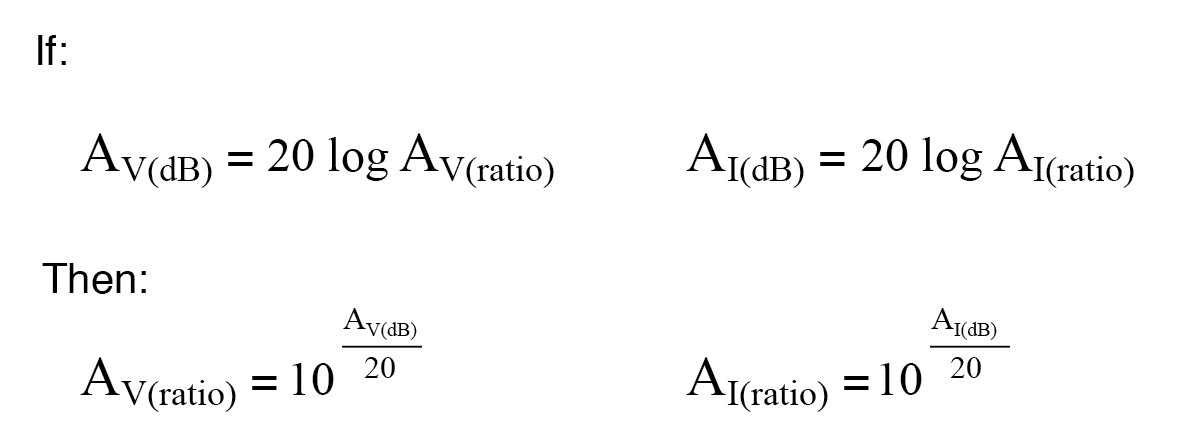
Si bien el bel es una unidad naturalmente escalada para la potencia, se ha inventado otra unidad logarítmica para expresar directamente las ganancias / pérdidas de voltaje o corriente, y se basa en el natural logaritmo en lugar del común logaritmo como bels y decibelios. Llamado el neper , su símbolo de unidad es “Np; sin embargo, se puede encontrar una "n" minúscula.

Para bien o para mal, ni el neper ni su primo atenuado, el decineper , se utiliza popularmente como unidad en aplicaciones de ingeniería estadounidenses. Ejemplo: El voltaje en un amplificador de línea de audio de 600 Ω es 10 mV, el voltaje en una carga de 600 Ω es 1 V. Encuentre la ganancia de potencia en dB.

 A (dB) =20 log10 (VO / VI) =20 log10 (1 /0.01) =20 log10 (100) =20 (2) =40 dB 

Ejemplo: Encuentre la relación de ganancia de voltaje AV (relación) =(VO / VI) para un amplificador de ganancia de 20 dB con una impedancia de entrada y salida de 50 Ω.

 AV (dB) =20 log10 AV (relación) 20 =20 log10 AV (relación) 20/20 =log10 AP (relación) 1020/20 =10log10 (AV (relación)) 10 =AV (relación) =( VO / VI) 

Una revisión del decibel

• Las ganancias y pérdidas pueden expresarse en términos de una relación sin unidades, o en la unidad de bels (B) o decibelios (dB). Un decibel es literalmente un deci -bel:una décima parte de un bel.
• El bel es fundamentalmente una unidad para expresar poder ganancia o pérdida. Para convertir una relación de potencia a belios o decibeles, utilice una de estas ecuaciones:

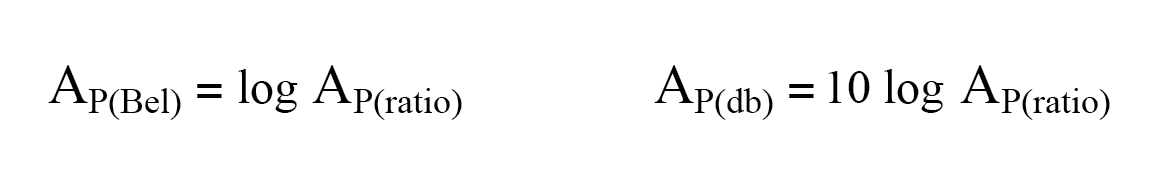
• Al usar la unidad de bel o decibelios para expresar un voltaje o actual proporción, debe emitirse en términos de un poder equivalente proporción. En la práctica, esto significa el uso de diferentes ecuaciones, con un factor de multiplicación de 2 para el valor del logaritmo correspondiente a un exponente de 2 para la relación de ganancia de voltaje o corriente:

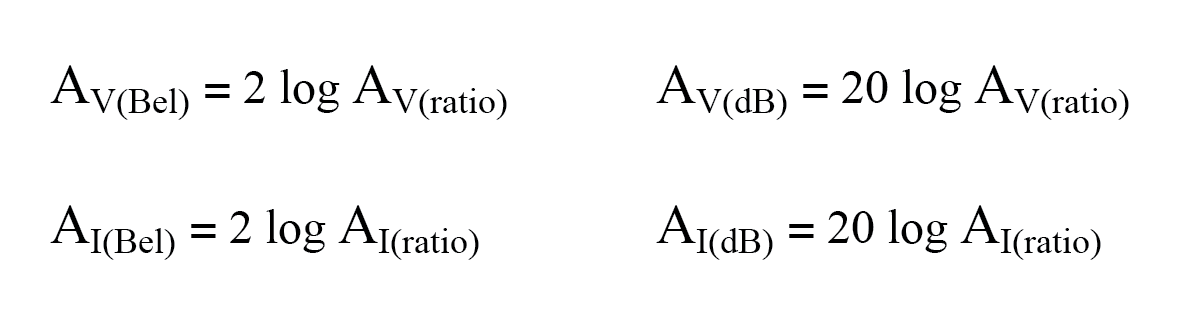
• Para convertir una ganancia de decibelios en una ganancia de relación sin unidades, use una de estas ecuaciones:

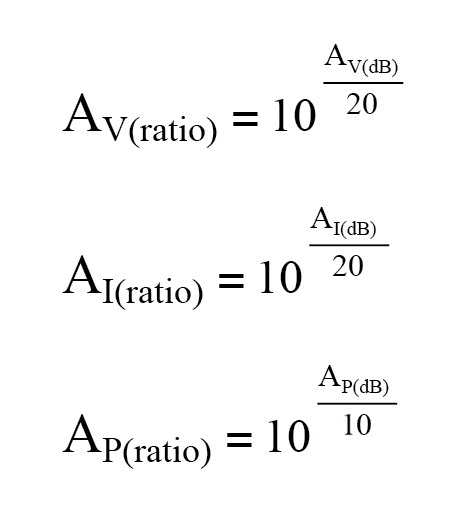
• Una ganancia (amplificación) se expresa como una cifra positiva de bel o decibelios. Una pérdida (atenuación) se expresa como una cifra negativa en bel o decibelios. La ganancia de unidad (sin ganancia o pérdida; relación =1) se expresa como cero belios o cero decibeles.
• Al calcular la ganancia general para un sistema de amplificación compuesto por múltiples etapas de amplificación, las relaciones de ganancia individuales se multiplican para encontrar la relación de ganancia general. Las cifras de bel o decibelios para cada etapa del amplificador, por otro lado, se agregan juntos para determinar la ganancia general.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de medidas de decibelios
• Hoja de trabajo de la teoría del amplificador elemental