Medición de frecuencia y fase

Una cantidad eléctrica importante sin equivalente en circuitos de CC es la frecuencia .

La medición de frecuencia es muy importante en muchas aplicaciones de corriente alterna, especialmente en sistemas de energía CA diseñados para funcionar de manera eficiente a una frecuencia y solo a una frecuencia.

Si la CA se genera mediante un alternador electromecánico, la frecuencia será directamente proporcional a la velocidad del eje de la máquina, y la frecuencia podría medirse simplemente midiendo la velocidad del eje.

Sin embargo, si es necesario medir la frecuencia a cierta distancia del alternador, serán necesarios otros medios de medición.

Método de medición de frecuencia

Uso del principio de resonancia mecánica

Un método simple pero tosco de medición de frecuencia en sistemas eléctricos utiliza el principio de resonancia mecánica. Todo objeto físico que posee la propiedad de elasticidad (elasticidad) tiene una frecuencia inherente a la que preferirá vibrar.

El diapasón es un gran ejemplo de esto:golpéalo una vez y seguirá vibrando en un tono específico para su longitud. Los diapasones más largos tienen frecuencias de resonancia más bajas:sus tonos serán más bajos en la escala musical que los diapasones más cortos.

Imagine una fila de diapasones de tamaño progresivo dispuestos uno al lado del otro. Todos están montados sobre una base común, y esa base se hace vibrar a la frecuencia del voltaje (o corriente) de CA medido por medio de un electroimán.

El diapasón que esté más cerca en frecuencia de resonancia a la frecuencia de esa vibración tenderá a temblar más (o más fuerte). Si los dientes de las horquillas fueran lo suficientemente endebles, podríamos ver el movimiento relativo de cada uno por la longitud del desenfoque que veríamos al inspeccionar cada uno desde una perspectiva de vista de extremo.

Bueno, haz una colección de "diapasones" con una tira de chapa cortada en un patrón similar a un rastrillo, y tienes la lengüeta vibratoria medidor de frecuencia:

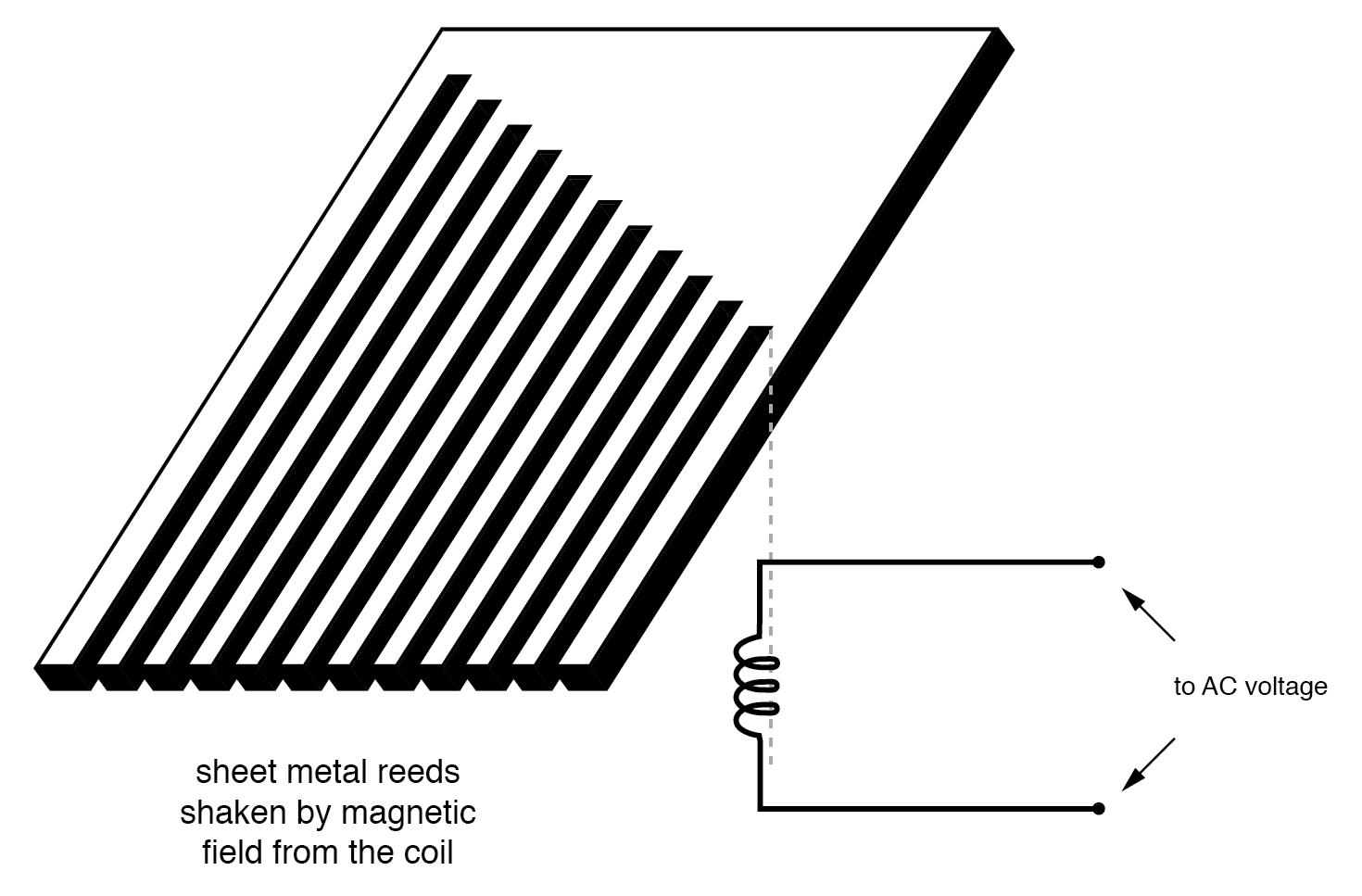
Diagrama del medidor de frecuencia de lengüeta vibratoria.

El usuario de este medidor ve los extremos de todas esas lengüetas de longitud desigual a medida que se agitan colectivamente a la frecuencia del voltaje de CA aplicado a la bobina. El más cercano en frecuencia de resonancia a la CA aplicada vibrará más, con un aspecto similar a:

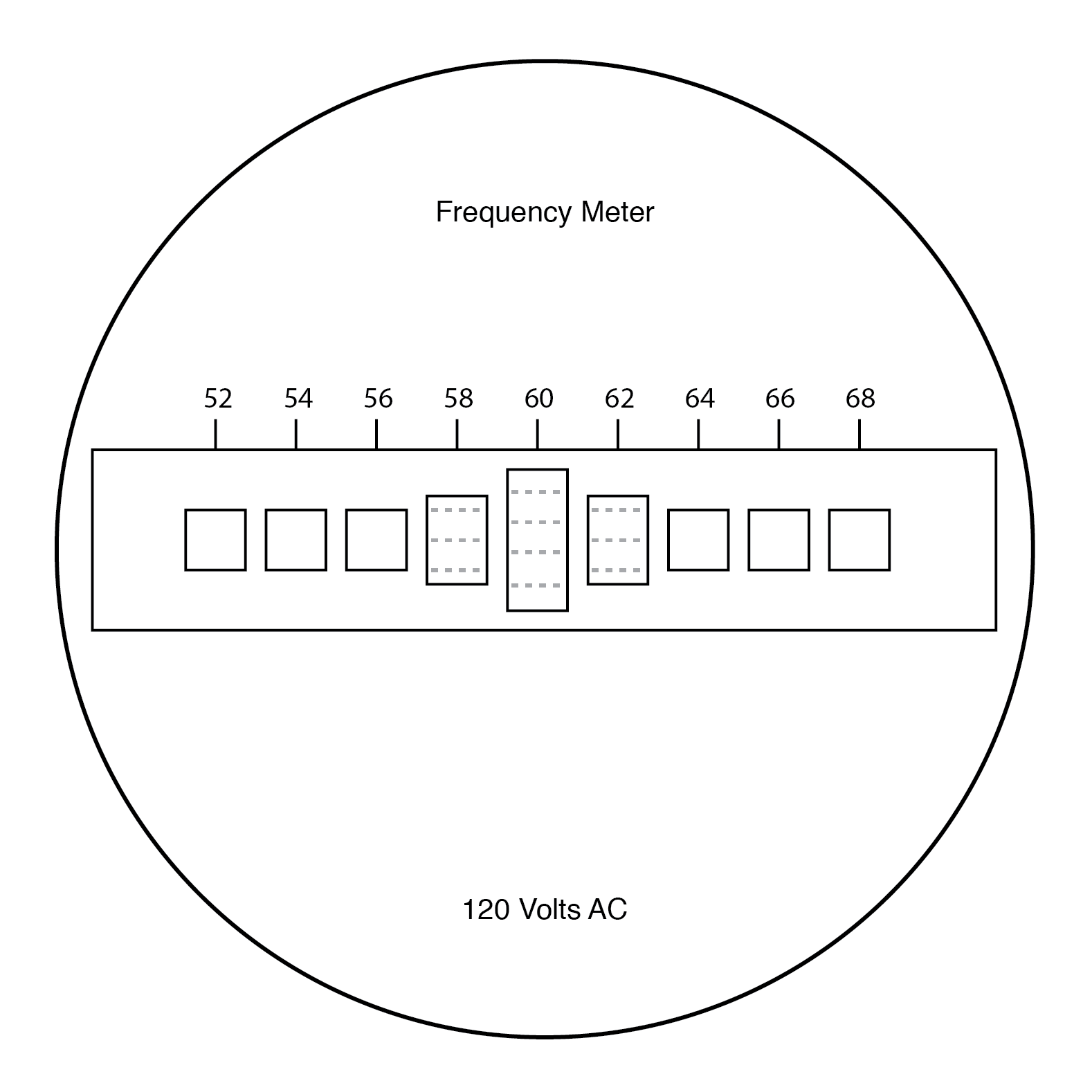
Panel frontal del medidor de frecuencia de lengüeta vibratoria.

Los medidores de lengüeta vibratoria, obviamente, no son instrumentos de precisión, pero son muy simples y, por lo tanto, fáciles de fabricar para que sean resistentes. A menudo se encuentran en pequeños grupos electrógenos accionados por motor con el fin de ajustar la velocidad del motor de modo que la frecuencia sea algo cercana a 60 (50 en Europa) Hertz.

Uso de una forma de circuito de tanque

Si bien los medidores tipo lengüeta son imprecisos, su principio operativo no lo es. En lugar de la resonancia mecánica, podemos sustituir la resonancia eléctrica y diseñar un medidor de frecuencia utilizando un inductor y un condensador en forma de circuito de tanque (inductor y condensador en paralelo). Consulte la figura siguiente.

Uno o ambos componentes se hacen ajustables y se coloca un medidor en el circuito para indicar la amplitud máxima del voltaje a través de los dos componentes.

Las perillas de ajuste están calibradas para mostrar la frecuencia de resonancia para cualquier configuración dada, y la frecuencia se lee después de que el dispositivo se ha ajustado para la indicación máxima en el medidor.

Esencialmente, este es un circuito de filtro sintonizable que se ajusta y luego se lee de una manera similar a un circuito puente (que debe equilibrarse para una condición "nula" y luego leerse).

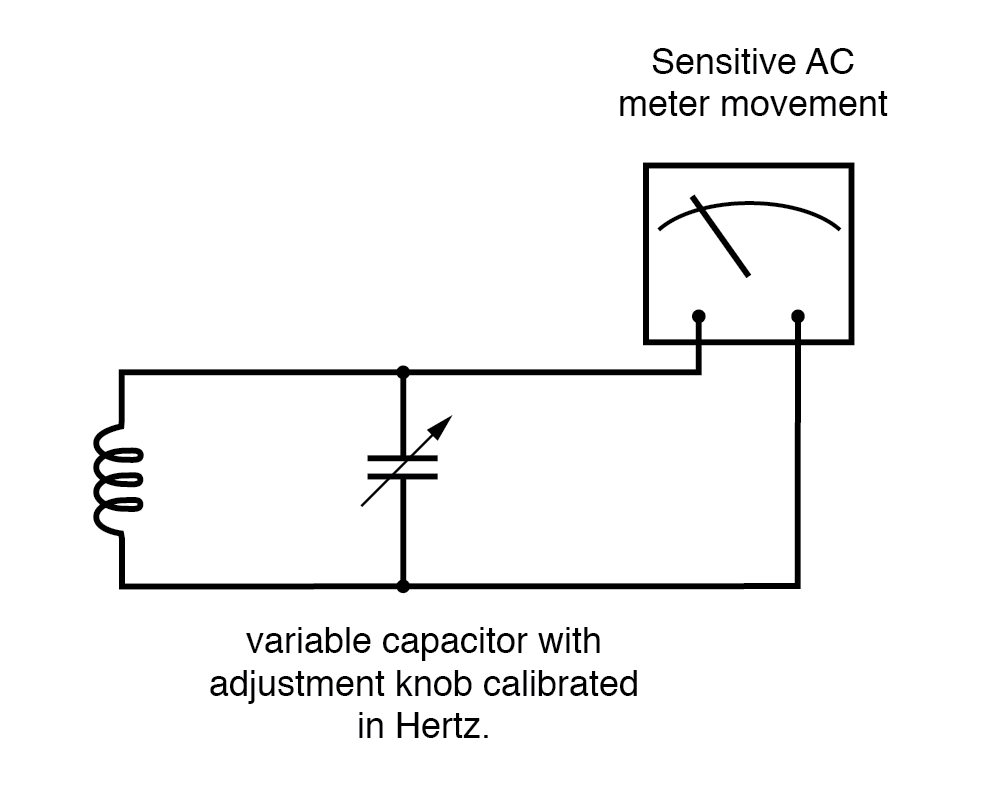
El medidor de frecuencia resonante "picos" cuando la frecuencia resonante L-C se sintoniza para probar la frecuencia.

Esta técnica es muy popular entre los radioaficionados (o al menos lo era antes de la llegada de instrumentos de frecuencia digital de bajo costo llamados contadores ). ), especialmente porque no requiere una conexión directa al circuito.

Siempre que el inductor y / o el capacitor puedan interceptar suficiente campo parásito (magnético o eléctrico, respectivamente) del circuito bajo prueba para hacer que el medidor indique, funcionará.

En frecuencia, como en otros tipos de medición eléctrica, los medios de medición más precisos suelen ser aquellos en los que se compara una cantidad desconocida con un estándar conocido. , el instrumento básico que no hace más que indicar cuando las dos cantidades son iguales.

Este es el principio básico detrás del circuito de puente de CC (Wheatstone) y es un principio metrológico sólido aplicado en todas las ciencias. Si tenemos acceso a un estándar de frecuencia preciso (una fuente de voltaje de CA que se mantiene con mucha precisión en una sola frecuencia), la medición de una frecuencia desconocida, en comparación, debería ser relativamente fácil.

Uso de cristal de cuarzo

Para ese estándar de frecuencia, volvemos nuestra atención al diapasón, o al menos a una variación más moderna llamada cristal de cuarzo .

El cuarzo es un mineral natural que posee una propiedad muy interesante llamada piezoelectricidad . Los materiales piezoeléctricos producen un voltaje en toda su longitud cuando se someten a tensión física y se deforman físicamente cuando se aplica un voltaje externo en toda su longitud.

Esta deformación es muy, muy leve en la mayoría de los casos, pero existe.

La roca de cuarzo es elástica (elástica) dentro de ese pequeño rango de flexión que produciría un voltaje externo, lo que significa que tendrá una frecuencia de resonancia mecánica propia capaz de manifestarse como una señal de voltaje eléctrico.

En otras palabras, si se golpea un chip de cuarzo, “sonará” con su propia frecuencia única determinada por la longitud del chip, y esa oscilación resonante producirá un voltaje equivalente en múltiples puntos del chip de cuarzo que se puede tocar. en mediante cables fijados a la superficie del chip.

De manera recíproca, el chip de cuarzo tenderá a vibrar más cuando es "excitado" por un voltaje de CA aplicado exactamente a la frecuencia correcta, al igual que las lengüetas de un medidor de frecuencia de lengüeta vibratoria.

Las virutas de roca de cuarzo se pueden cortar con precisión para obtener las frecuencias de resonancia deseadas, y ese chip se monta de forma segura dentro de una carcasa protectora con cables que se extienden para la conexión a un circuito eléctrico externo.

Cuando se empaqueta como tal, el dispositivo resultante simplemente se llama cristal (oa veces " xtal ”). El símbolo esquemático se muestra en la siguiente figura.

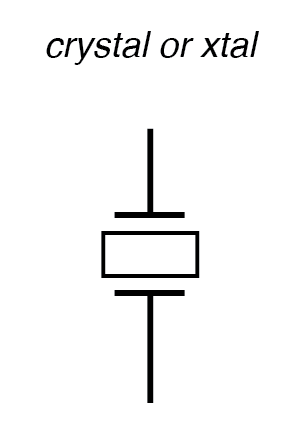
Símbolo esquemático de cristal (elemento determinante de frecuencia).

Eléctricamente, ese chip de cuarzo es equivalente a un circuito resonante LC en serie. (Figura siguiente) Las propiedades dieléctricas del cuarzo contribuyen con un elemento capacitivo adicional al circuito equivalente.

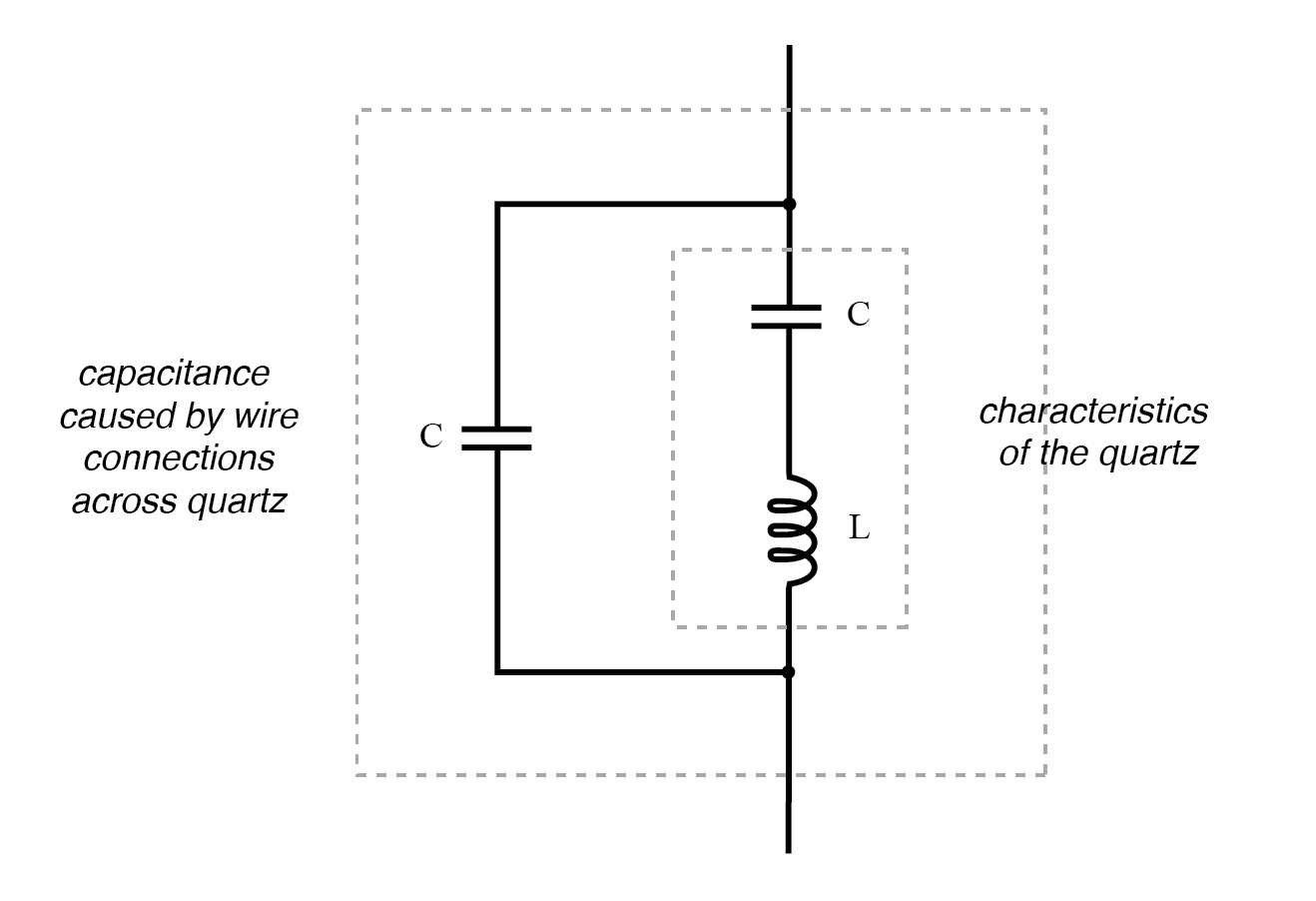
Circuito equivalente de cristal de cuarzo.

La "capacitancia" y la "inductancia" mostradas en serie son simplemente equivalentes eléctricos de las propiedades de resonancia mecánica del cuarzo:no existen como componentes discretos dentro del cristal. La capacitancia mostrada en paralelo debido a las conexiones de cables a través del cuerpo de cuarzo dieléctrico (aislante) es real y tiene un efecto en la respuesta resonante de todo el sistema.

Aquí no es necesaria una discusión completa sobre la dinámica de los cristales, pero lo que debe entenderse sobre los cristales es esta equivalencia del circuito resonante y cómo se puede explotar dentro de un circuito oscilador para lograr un voltaje de salida con una frecuencia conocida estable.

Los cristales, como elementos resonantes, suelen tener una "Q" ( calidad ) valores que los circuitos de tanque construidos a partir de inductores y condensadores, principalmente debido a la relativa ausencia de resistencia parásita, lo que hace que sus frecuencias de resonancia sean muy definidas y precisas.

Debido a que la frecuencia de resonancia depende únicamente de las propiedades físicas del cuarzo (una sustancia muy estable, mecánicamente), la variación de la frecuencia de resonancia a lo largo del tiempo con un cristal de cuarzo es muy, muy baja. Así es como el movimiento de cuarzo los relojes obtienen su alta precisión:mediante un oscilador electrónico estabilizado por la acción resonante de un cristal de cuarzo.

Sin embargo, para aplicaciones de laboratorio, se puede desear una estabilidad de frecuencia aún mayor. Para lograr esto, el cristal en cuestión puede colocarse en un ambiente con temperatura estabilizada (generalmente un horno), eliminando así los errores de frecuencia debidos a la expansión y contracción térmica del cuarzo.

Sin embargo, para lo último en un estándar de frecuencia, nada descubierto hasta ahora supera la precisión de un solo átomo resonante. Este es el principio del llamado reloj atómico , que utiliza un átomo de mercurio (o cesio) suspendido en el vacío, excitado por energía exterior para resonar en su propia frecuencia única.

La frecuencia resultante se detecta como una señal de ondas de radio y eso forma la base de los relojes más precisos conocidos por la humanidad. Los laboratorios de estándares nacionales de todo el mundo mantienen algunos de estos relojes hiperprecisos y transmiten señales de frecuencia basadas en las vibraciones de esos átomos para que los científicos y técnicos sintonicen y utilicen con fines de calibración de frecuencia.

Parte práctica

Ahora llegamos a la parte práctica:una vez que tengamos una fuente de frecuencia precisa, ¿cómo lo comparamos con una frecuencia desconocida para obtener una medición?

Una forma es utilizar un CRT como dispositivo de comparación de frecuencias. Los tubos de rayos catódicos suelen tener medios para desviar el haz de electrones tanto en el eje horizontal como en el vertical.

Si se utilizan placas de metal para desviar electrostáticamente los electrones, habrá un par de placas a la izquierda y a la derecha del haz, así como un par de placas por encima y por debajo del haz, como se muestra en la figura siguiente.

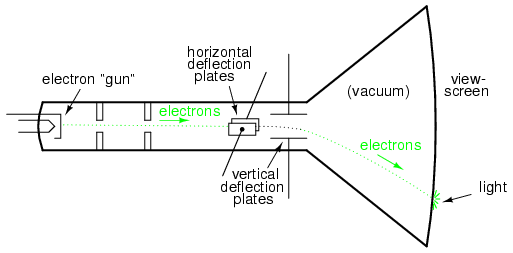
Tubo de rayos catódicos (CRT) con placas deflectoras verticales y horizontales.

Si permitimos que una señal de CA desvíe el rayo hacia arriba y hacia abajo (conecte esa fuente de voltaje de CA a las placas de deflexión "verticales") y otra señal de CA para desviar el haz de izquierda a derecha (utilizando el otro par de placas de deflexión), los patrones aparecerán. ser producido en la pantalla del CRT indicativo de la relación de estas dos frecuencias de CA.

Estos patrones se denominan figuras de Lissajous y son un medio común de medición de frecuencia comparativa en electrónica.

Si las dos frecuencias son iguales, obtendremos una figura simple en la pantalla del CRT, la forma de esa figura depende del cambio de fase entre las dos señales de CA. Aquí hay una muestra de las cifras de Lissajous para dos señales de onda sinusoidal de igual frecuencia, mostradas como aparecerían en la cara de un osciloscopio (un instrumento de medición de voltaje de CA que usa un CRT como su "movimiento").

La primera imagen es de la figura de Lissajous formada por dos voltajes de CA perfectamente en fase entre sí:

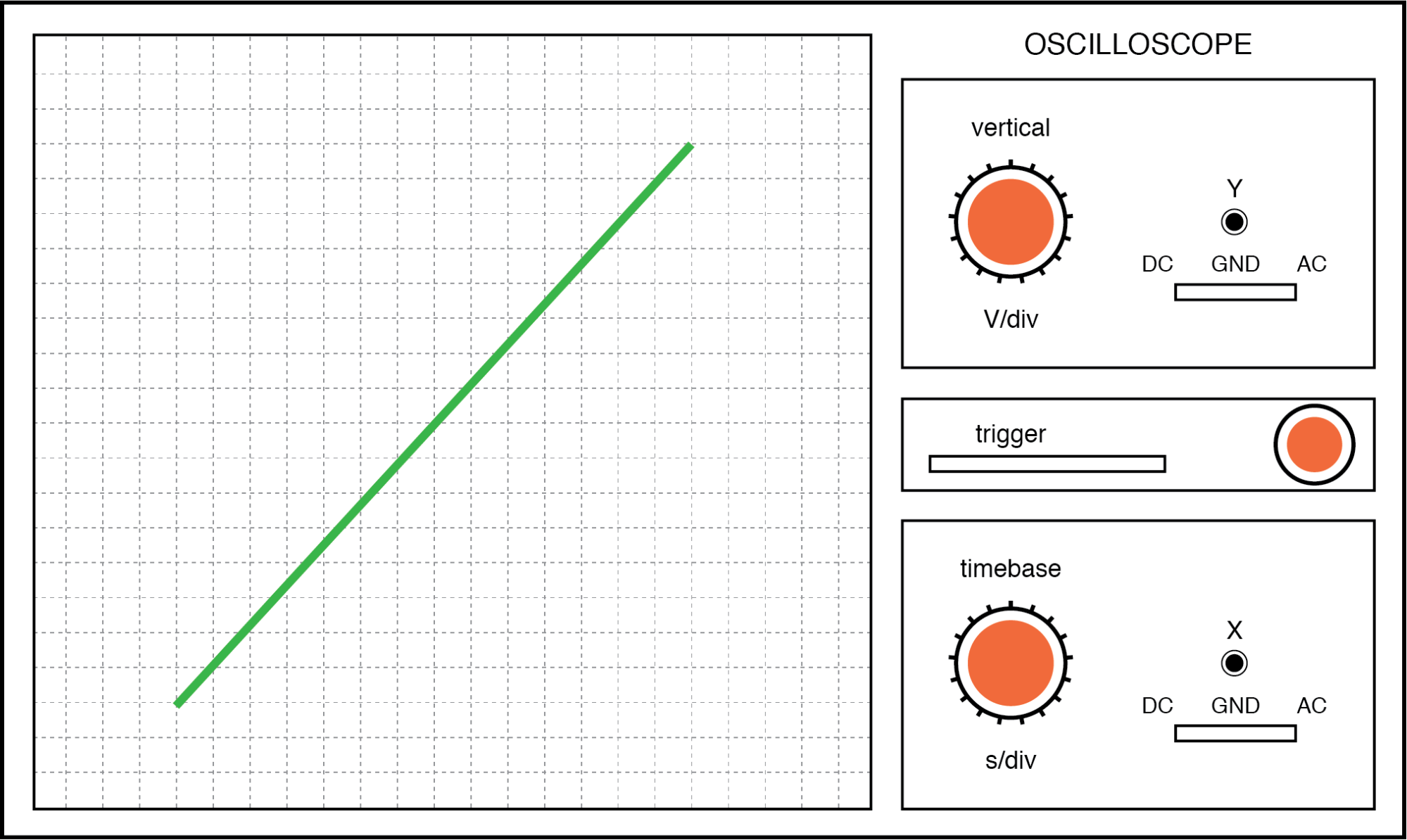
Figura de Lissajous:misma frecuencia, cambio de fase de cero grados.

Si los dos voltajes de CA no están en fase entre sí, no se formará una línea recta. Más bien, la figura de Lissajous tomará la apariencia de un óvalo, volviéndose perfectamente circular si el cambio de fase es exactamente de 90 ° entre las dos señales, y si sus amplitudes son iguales:

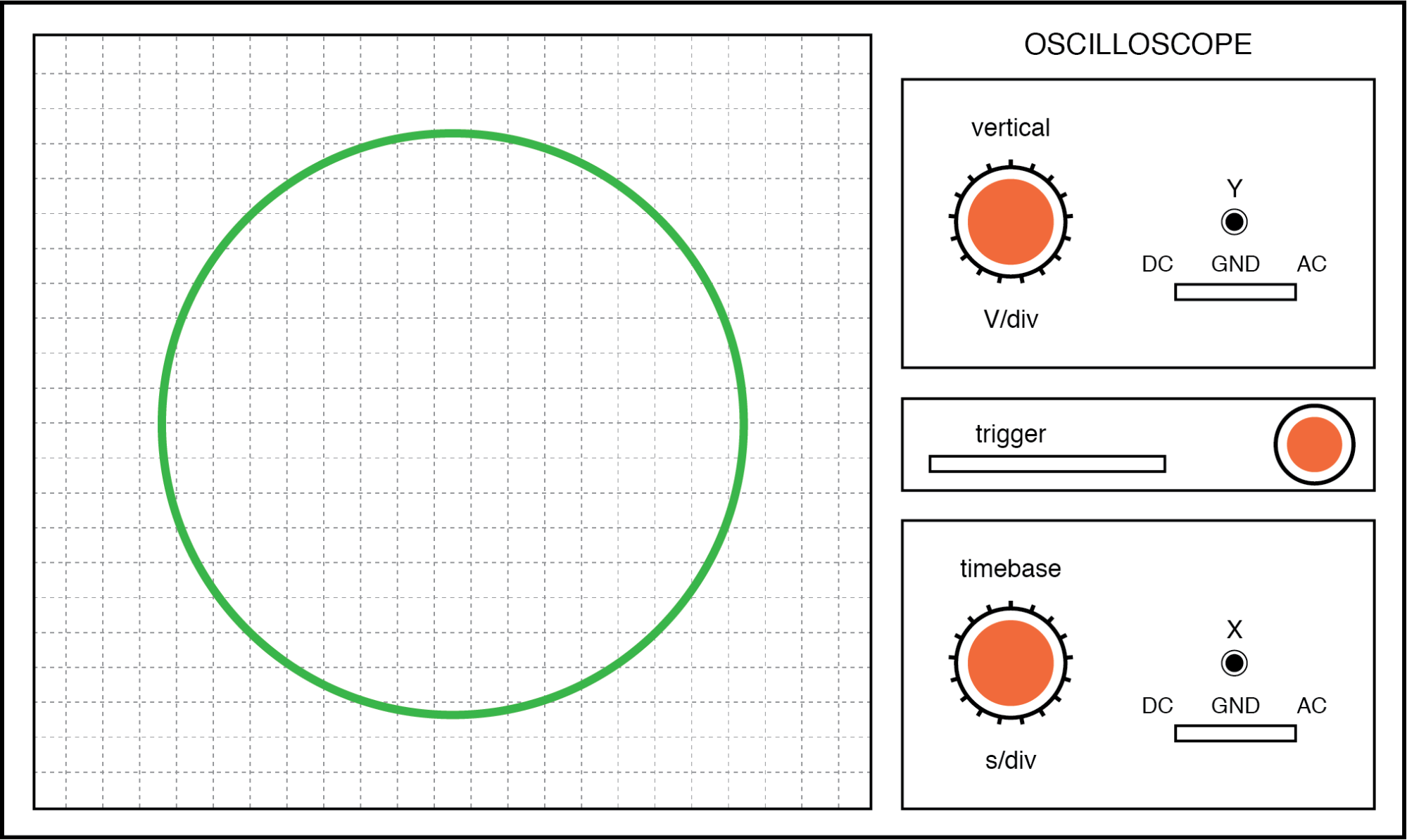
Figura de Lissajous:misma frecuencia, cambio de fase de 90 o 270 grados.

Finalmente, si las dos señales de CA se oponen directamente entre sí en fase (cambio de 180 °), terminaremos con una línea nuevamente, solo que esta vez estará orientada en la dirección opuesta:

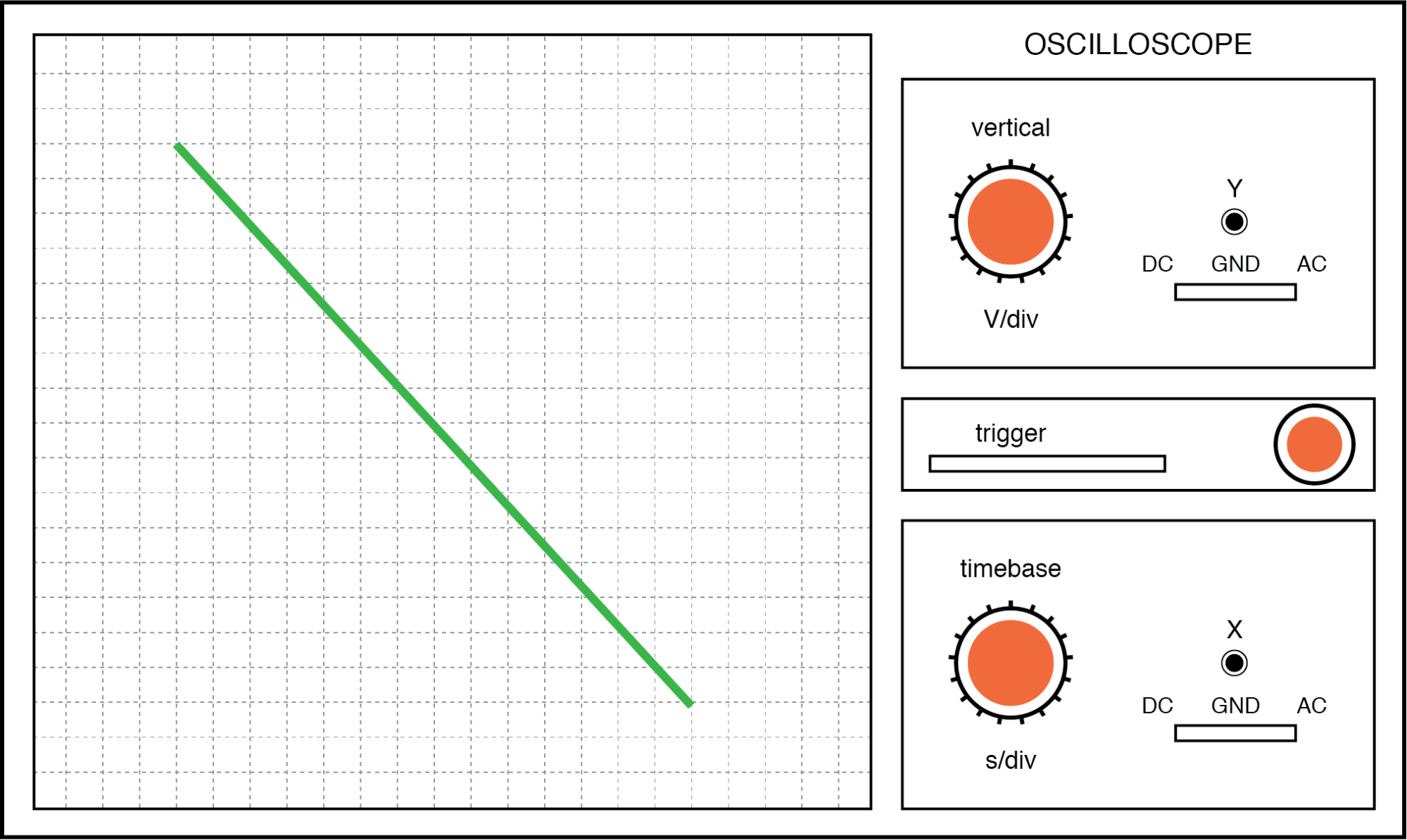
Figura de Lissajous:misma frecuencia, cambio de fase de 180 grados.

Cuando nos enfrentamos a frecuencias de señal que no son las mismas, las cifras de Lissajous se vuelven un poco más complejas. Considere los siguientes ejemplos y se les dan relaciones de frecuencia vertical / horizontal:

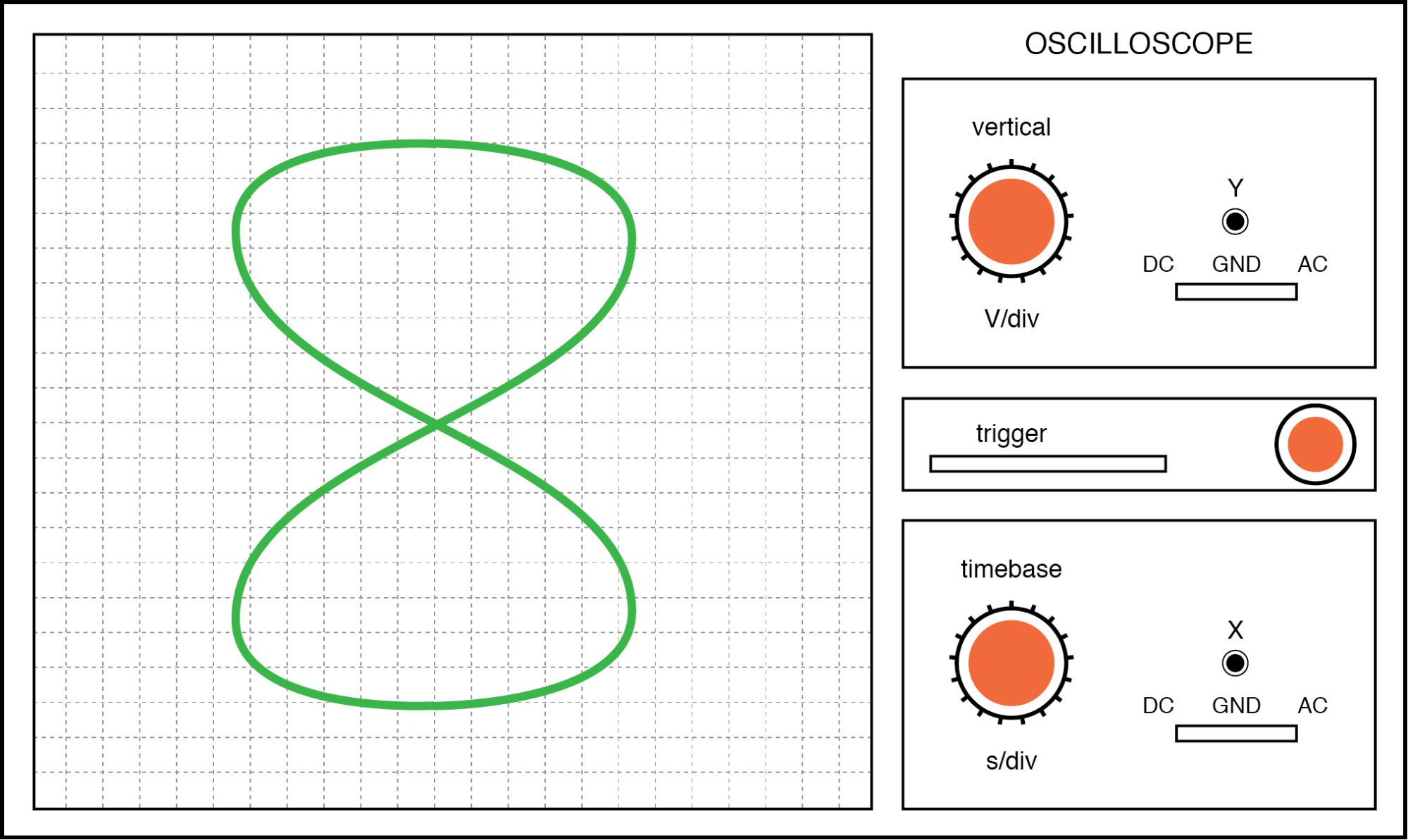
Figura de Lissajous:la frecuencia horizontal es el doble que la vertical.

Cuanto más compleja sea la relación entre las frecuencias horizontales y verticales, más compleja será la figura de Lissajous. Considere la siguiente ilustración de una relación de frecuencia de 3:1 entre horizontal y vertical:

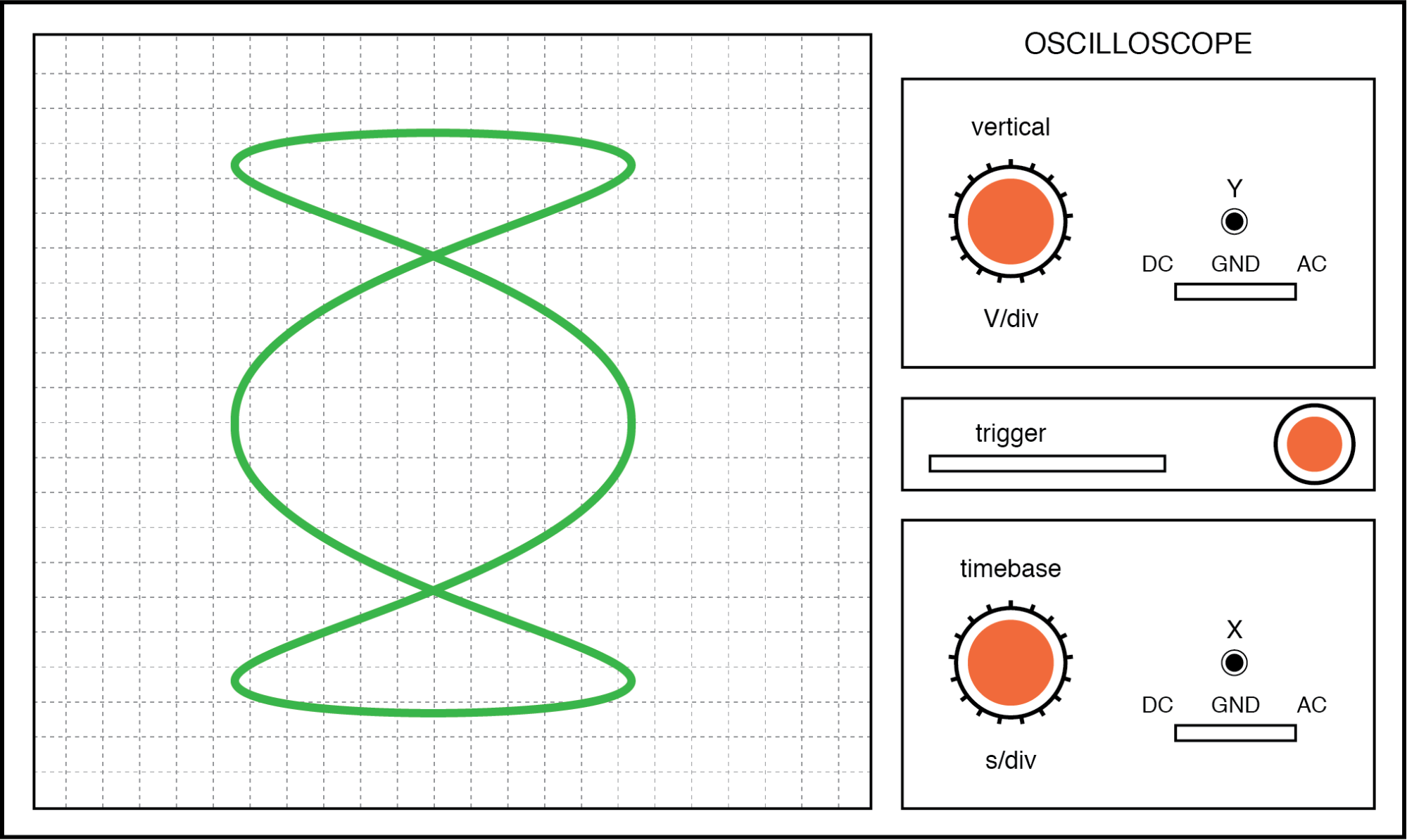
Figura de Lissajous:la frecuencia horizontal es tres veces mayor que la vertical.

. . . y una relación de frecuencia de 3:2 (horizontal =3, vertical =2) en la siguiente figura.

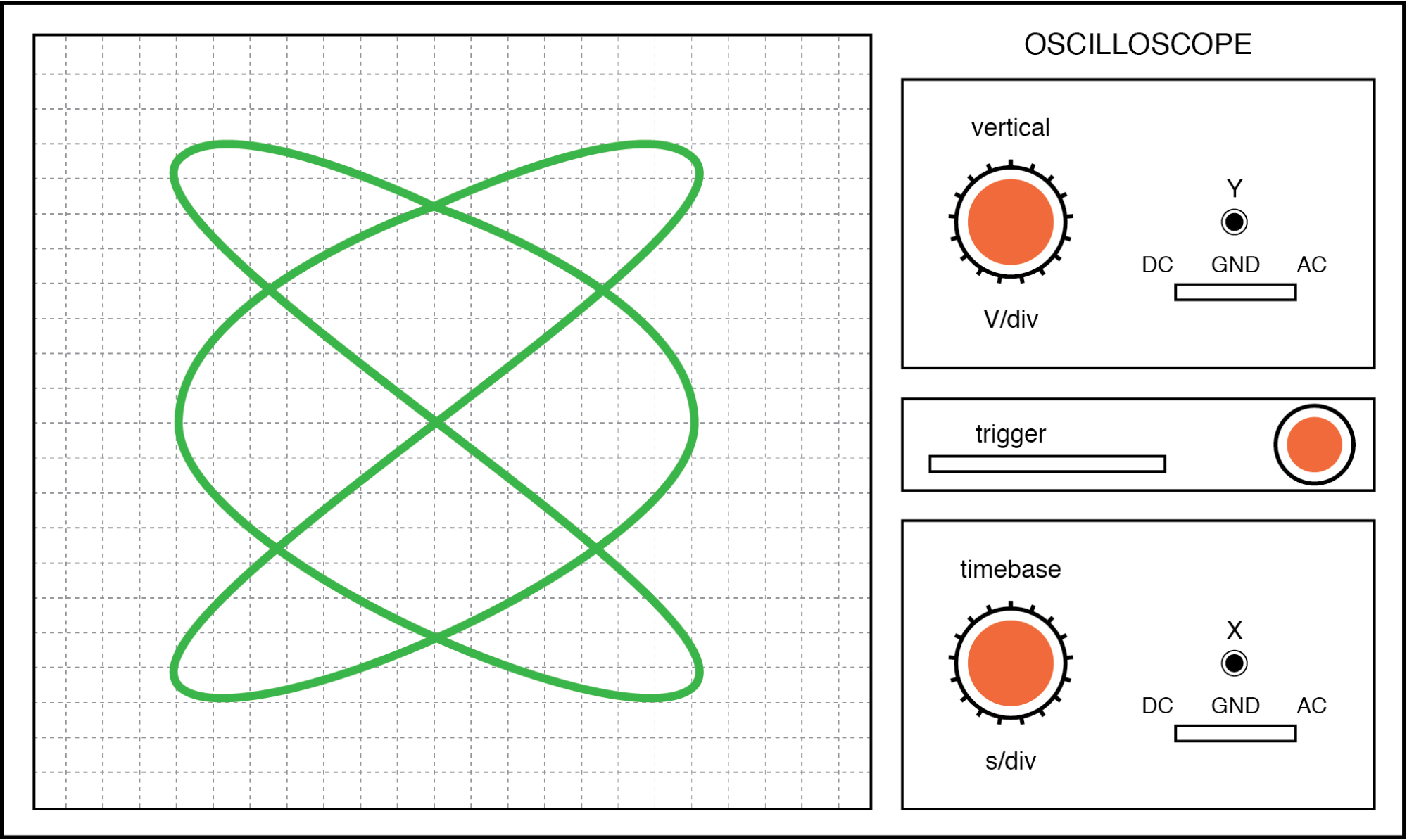
Figura de Lissajous:la relación de frecuencia horizontal / vertical es 3:2.

En los casos en que las frecuencias de las dos señales de CA no sean exactamente una relación simple entre sí (pero cercanas), la figura de Lissajous parecerá "moverse", cambiando lentamente de orientación a medida que el ángulo de fase entre las dos formas de onda se desplaza entre 0 ° y 180 °.

Si las dos frecuencias están bloqueadas en una proporción entera exacta entre sí, la figura de Lissajous se mantendrá estable en la pantalla de visualización del CRT.

La física de las figuras de Lissajous limita su utilidad como técnica de comparación de frecuencias a los casos en los que las relaciones de frecuencia son valores enteros simples (1:1, 1:2, 1:3, 2:3, 3:4, etc.).

A pesar de esta limitación, las cifras de Lissajous son un medio popular de comparación de frecuencias dondequiera que exista un estándar de frecuencia accesible (generador de señales).

REVISAR:

• Algunos medidores de frecuencia funcionan según el principio de resonancia mecánica, que indica la frecuencia mediante una oscilación relativa entre un conjunto de "lengüetas" sintonizadas de manera única que se agitan a la frecuencia medida.
• Otros medidores de frecuencia usan circuitos resonantes eléctricos (circuitos de tanque LC, generalmente) para indicar la frecuencia. Uno o ambos componentes están hechos para ser ajustables, con una perilla de ajuste calibrada con precisión, y un medidor sensible lee el voltaje o la corriente máxima en el punto de resonancia.
• La frecuencia se puede medir de manera comparativa, como es el caso cuando se usa un CRT para generar figuras de Lissajous. Las señales de frecuencia de referencia se pueden generar con un alto grado de precisión mediante circuitos osciladores que utilizan cristales de cuarzo como dispositivos resonantes. Para lograr una ultraprecisión, se pueden utilizar estándares de señal de reloj atómico (basados ​​en las frecuencias de resonancia de los átomos individuales).