Atenuadores

¿Qué son los atenuadores?

Los atenuadores son dispositivos pasivos. Es conveniente discutirlos junto con los decibelios. Los atenuadores debilitan o atenúan la salida de alto nivel de un generador de señales, por ejemplo, para proporcionar una señal de nivel más bajo para algo como la entrada de antena de un receptor de radio sensible. (figura siguiente) El atenuador podría estar integrado en el generador de señal o ser un dispositivo independiente. Podría proporcionar una cantidad de atenuación fija o ajustable. Una sección de atenuador también puede proporcionar aislamiento entre una fuente y una carga problemática.

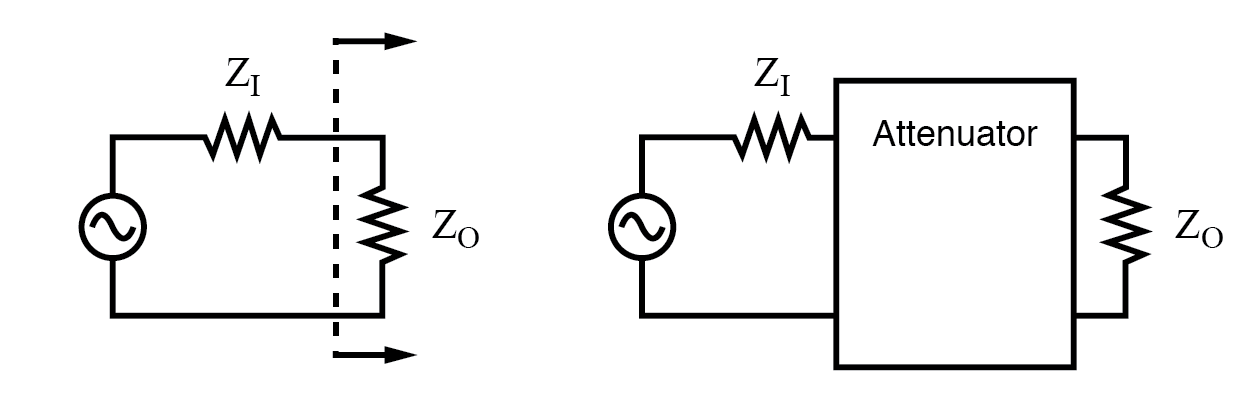
El atenuador de impedancia constante se adapta a la impedancia de la fuente ZI y la impedancia de carga ZO. Para equipos de radiofrecuencia, Z es 50 Ω.

En el caso de un atenuador independiente, debe colocarse en serie entre la fuente de señal y la carga abriendo la ruta de la señal como se muestra en la figura anterior. Además, debe coincidir con la impedancia de la fuente Z Yo y la impedancia de carga Z O , mientras proporciona una cantidad específica de atenuación. En esta sección solo consideraremos el caso especial y más común en el que las impedancias de fuente y carga son iguales. No se considera en esta sección, la fuente desigual y las impedancias de carga pueden coincidir con una sección de atenuador. Sin embargo, la formulación es más compleja.

Los atenuadores de sección T y sección Π son formas comunes.

Las configuraciones comunes son T y Π redes que se muestran en la figura anterior. Se pueden conectar en cascada múltiples secciones de atenuador cuando se necesitan señales aún más débiles, como se muestra en la siguiente figura.

Uso de decibelios para atenuadores

Las relaciones de voltaje, como se utilizan en el diseño de atenuadores, a menudo se expresan en términos de decibeles. La relación de voltaje debe derivarse de la atenuación en decibelios. Las relaciones de potencia expresadas en decibelios son aditivas. Por ejemplo, un atenuador de 10 dB seguido de un atenuador de 6 dB proporciona 16 dB de atenuación en general.

10 dB + 6 db =16 dB

Los niveles de sonido cambiantes son perceptibles aproximadamente proporcionales al logaritmo de la relación de potencia (PI / PO).

nivel de sonido =log10 (PI / PO)

Un cambio de 1 dB en el nivel de sonido es apenas perceptible para un oyente, mientras que 2 db son fácilmente perceptibles. Una atenuación de 3dB corresponde a reducir la potencia a la mitad, mientras que una ganancia de 3 db corresponde a una duplicación del nivel de potencia. Una ganancia de -3 dB es lo mismo que una atenuación de +3 dB, correspondiente a la mitad del nivel de potencia original.

El cambio de potencia en decibelios en términos de relación de potencia es:

dB =10 log10 (PI / PO)

Suponiendo que la carga RI en PI es la misma que la resistencia de carga RO en PO (RI =RO), los decibelios pueden derivarse de la relación de voltaje (VI / VO) o la relación de corriente (II / IO):

PO =VO IO =VO2 / R =IO2 R PI =VI II =VI2 / R =II2 R dB =10 log10 (PI / PO) =10 log10 (VI2 / VO2) =20 log10 (VI / VO) dB =10 log10 (PI / PO) =10 log10 (II2 / IO2) =20 log10 (II / IO)

Ecuaciones en decibelios

Las dos formas más utilizadas de la ecuación de decibelios son:

dB =10 log10 (PI / PO) o dB =20 log10 (VI / VO)

Usaremos la última forma, ya que necesitamos la relación de voltaje. Una vez más, la forma de ecuación de relación de voltaje solo es aplicable cuando las dos resistencias correspondientes son iguales. Es decir, la fuente y la resistencia de carga deben ser iguales.

Ejemplos que utilizan las ecuaciones en decibelios

Ejemplo: La potencia en un atenuador es de 10 vatios, la potencia de salida es de 1 vatio. Encuentre la atenuación en dB.

dB =10 log10 (PI / PO) =10 log10 (10/1) =10 log10 (10) =10 (1) =10 dB

Ejemplo: Encuentre la relación de atenuación de voltaje (K =(VI / VO)) para un atenuador de 10 dB.

dB =10 =20 log10 (VI / VO) 10/20 =log10 (VI / VO) 1010/20 =10log10 (VI / VO) 3.16 =(VI / VO) =​​AP (relación)

Ejemplo: La potencia en un atenuador es de 100 milivatios, la potencia de salida es de 1 milivatio. Encuentre la atenuación en dB.

dB =10 log10 (PI / PO) =10 log10 (100/1) =10 log10 (100) =10 (2) =20 dB

Ejemplo: Encuentre la relación de atenuación de voltaje (K =(VI / VO)) para un atenuador de 20 dB.

dB =20 =20 log10 (VI / VO) 1020/20 =10 log10 (VI / VO) 10 =(VI / VO) =​​K

Atenuador de sección en T

Los atenuadores T y Π deben estar conectados a una Z fuente y Z impedancia de carga. La Z - (flechas) que apuntan en dirección opuesta al atenuador en la figura siguiente indican esto. La Z - (flechas) apuntando hacia el atenuador indica que la impedancia vista mirando hacia el atenuador con una carga Z en el extremo opuesto es Z, Z =50 Ω para nuestro caso. Esta impedancia es una constante (50 Ω) con respecto a la atenuación; la impedancia no cambia cuando se cambia la atenuación.

La tabla de la figura siguiente enumera los valores de resistencia para T y Π atenuadores para que coincidan con una fuente / carga de 50 Ω, como es el requisito habitual en el trabajo de radiofrecuencia.

Los servicios de telefonía y otros trabajos de audio a menudo requieren una coincidencia de 600 Ω. Multiplica todo R valores por la relación (600/50) para corregir la coincidencia de 600 Ω. Multiplicar por 75/50 convertiría los valores de la tabla para que coincidan con una fuente y una carga de 75 Ω.

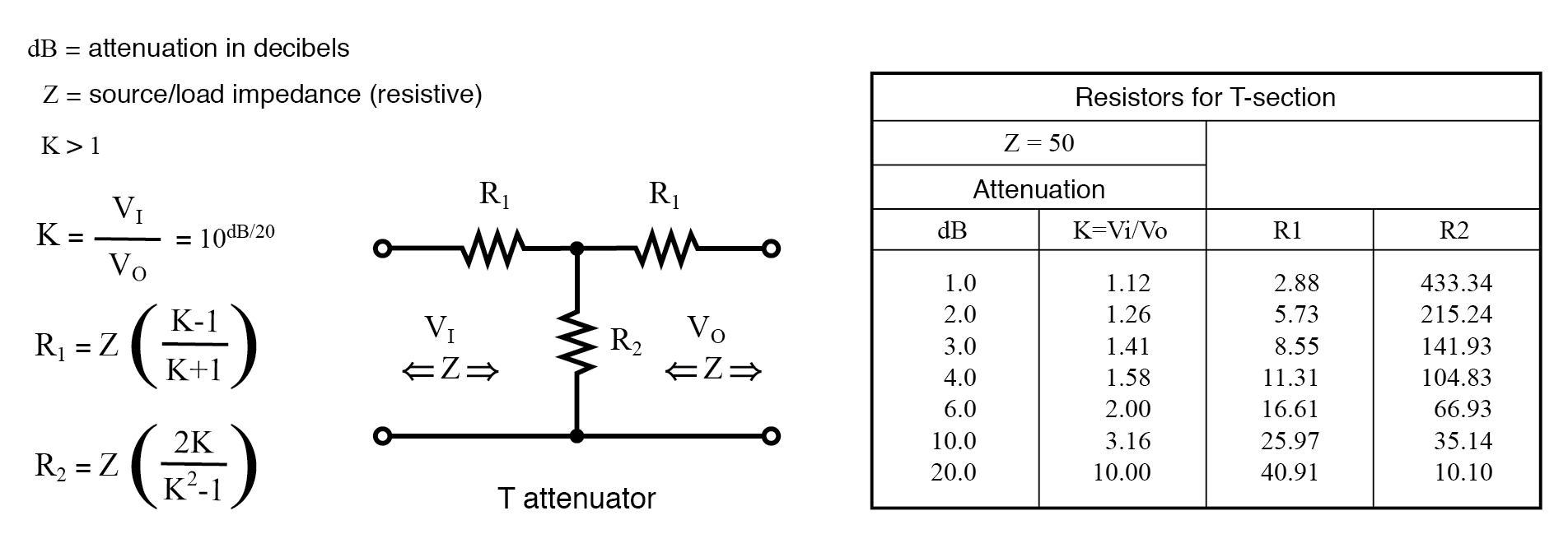
Fórmulas para resistencias de atenuación de sección en T, dado K, la relación de atenuación de voltaje y ZI =ZO =50 Ω.

La cantidad de atenuación se especifica habitualmente en dB (decibeles). Sin embargo, necesitamos la relación de voltaje (o corriente) K para encontrar los valores de resistencia a partir de ecuaciones. Ver dB / 20 término en el poder de 10 término para calcular la relación de voltaje K desde dB, arriba.

El T (y por debajo de Π ) las configuraciones se utilizan con mayor frecuencia, ya que proporcionan coincidencia bidireccional. Es decir, la entrada y salida del atenuador pueden intercambiarse de un extremo a otro y aún así coincidir con las impedancias de la fuente y la carga mientras se proporciona la misma atenuación.

Desconectando la fuente y mirando hacia la derecha en V Yo , necesitamos ver una combinación en serie en paralelo de R 1 , R 2 , R 1 y Z parece una resistencia equivalente de Z EN , lo mismo que la impedancia de fuente / carga Z:(una carga de Z está conectada a la salida).

ZIN =R1 + (R2 || (R1 + Z))

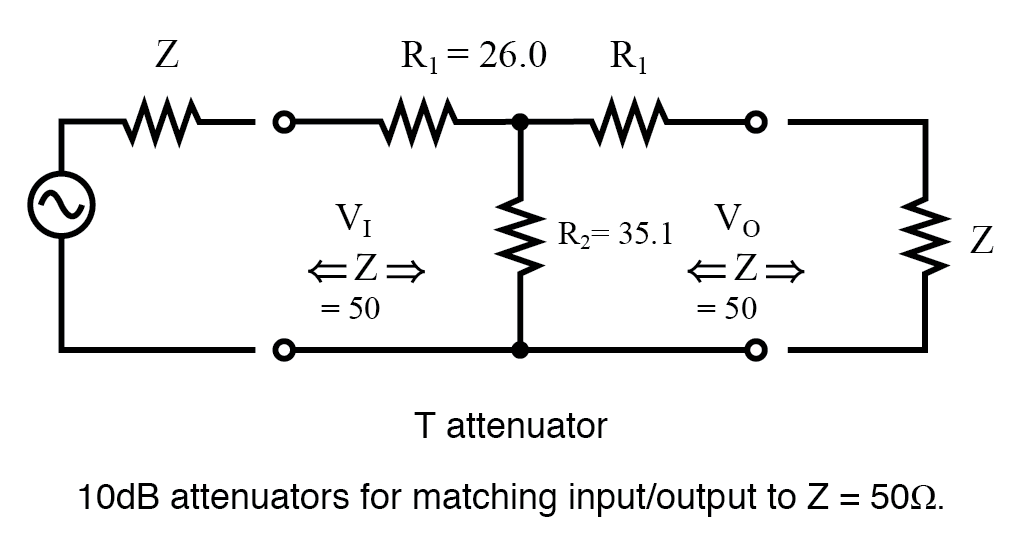
Por ejemplo, sustituya los valores de 10 dB de la tabla de atenuadores de 50 Ω por R 1 y R 2 como se muestra en la figura siguiente.

ZIN =25,97 + (35,14 || (25,97 + 50)) ZIN =25,97 + (35,14 || 75,97) ZIN =25,97 + 24,03 =50

Esto nos muestra que vemos 50 Ω mirando directamente al atenuador de ejemplo (figura siguiente) con una carga de 50 Ω.

Reemplazo del generador de fuente, desconectando la carga Z en V O , y mirando hacia la izquierda, debería darnos la misma ecuación que la anterior para la impedancia en V O , debido a la simetría. Además, las tres resistencias deben ser valores que proporcionen la atenuación requerida de entrada a salida. Esto se logra mediante las ecuaciones para R 1 y R 2 anterior según se aplica a la T -atenuador a continuación.

Atenuador de sección PI

La tabla de la figura siguiente enumera los valores de resistencia para Π atenuador que coincide con una fuente / carga de 50 Ω en algunos niveles de atenuación comunes. Las resistencias correspondientes a otros niveles de atenuación se pueden calcular a partir de las ecuaciones.

Fórmulas para resistencias de atenuación de sección Π, dado K, la relación de atenuación de voltaje y ZI =ZO =50 Ω.

Lo anterior se aplica al atenuador π a continuación.

¿Qué valores de resistencia se requerirían tanto para Π atenuadores para 10 dB de atenuación que coinciden con una fuente y carga de 50 Ω?

Ejemplo de atenuador de sección Π de 10 dB para hacer coincidir una fuente y una carga de 50 Ω.

Los 10 dB corresponde a una relación de atenuación de tensión de K =3,16 en la penúltima línea de la tabla anterior. Transfiera los valores de la resistencia en esa línea a las resistencias en el diagrama esquemático en la figura anterior.

Atenuador de sección en L

La tabla de la figura siguiente enumera los valores de resistencia para L atenuadores para que coincidan con una fuente / carga de 50 Ω. La tabla de la figura siguiente también enumera los valores de resistencia para una forma alternativa. Tenga en cuenta que los valores de la resistencia no son los mismos.

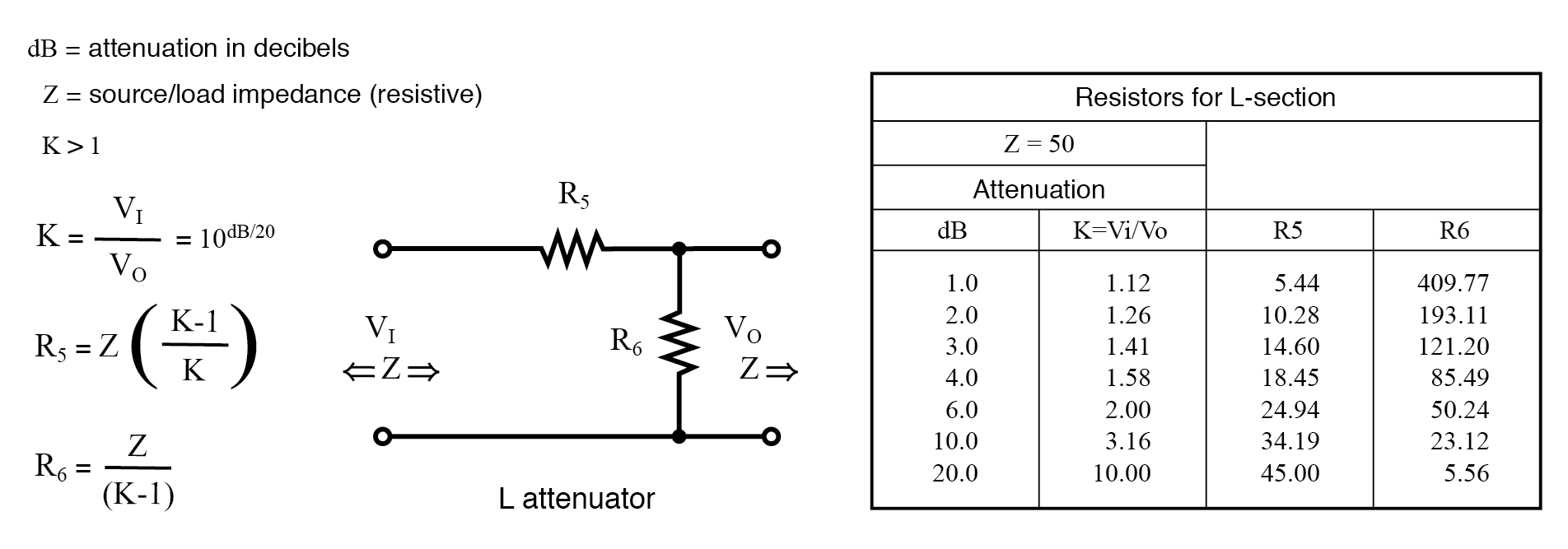
Tabla de atenuador de sección en L para fuente de 50 Ω e impedancia de carga.

Lo anterior se aplica a la L atenuador a continuación.

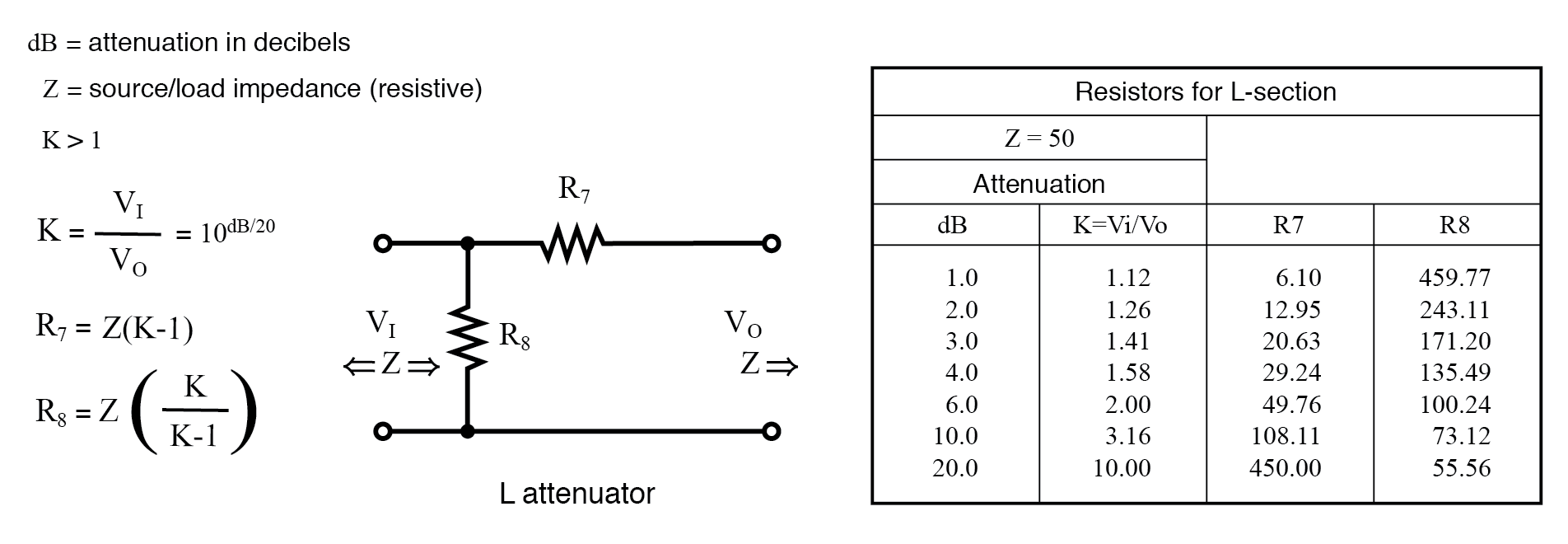
Tabla de atenuador de sección en L de forma alternativa para una fuente de 50 Ω y una impedancia de carga.

Atenuador T puente

La tabla de la figura siguiente enumera los valores de resistencia para el T puenteado atenuadores para que coincidan con una fuente y una carga de 50 Ω. El atenuador de puente en T no se utiliza a menudo. ¿Por qué no?

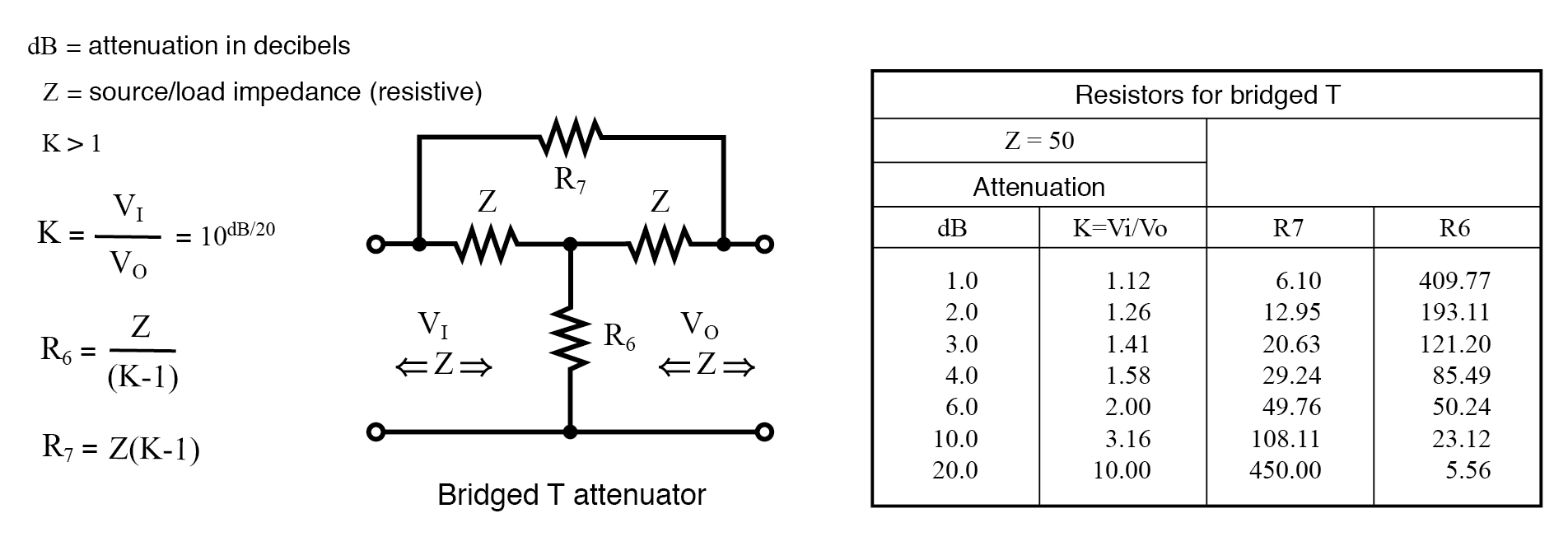
Fórmulas y tabla abreviada para la sección del atenuador en T puenteada, Z =50 Ω.

Secciones en cascada

Las secciones del atenuador se pueden conectar en cascada como se muestra en la figura siguiente para obtener más atenuación de la que puede estar disponible en una sola sección. Por ejemplo, dos atenuadores de 10 db pueden conectarse en cascada para proporcionar 20 dB de atenuación, siendo los valores de dB aditivos. La relación de atenuación de voltaje K o V Yo / V O para una sección de atenuador de 10 dB es 3,16. La relación de atenuación de voltaje para las dos secciones en cascada es el producto de las dos K so 3.16x3.16 =10 para las dos secciones en cascada.

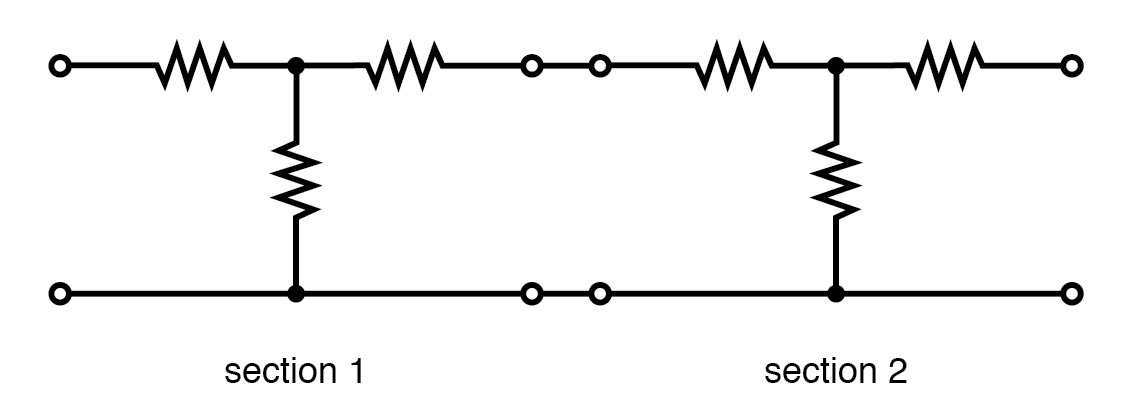
Secciones de atenuador en cascada:la atenuación en dB es aditiva.

Se puede proporcionar atenuación variable en pasos discretos mediante un atenuador conmutado. El ejemplo de la figura siguiente, que se muestra en la posición de 0 dB, es capaz de atenuar de 0 a 7 dB mediante la conmutación aditiva de ninguna, una o más secciones.

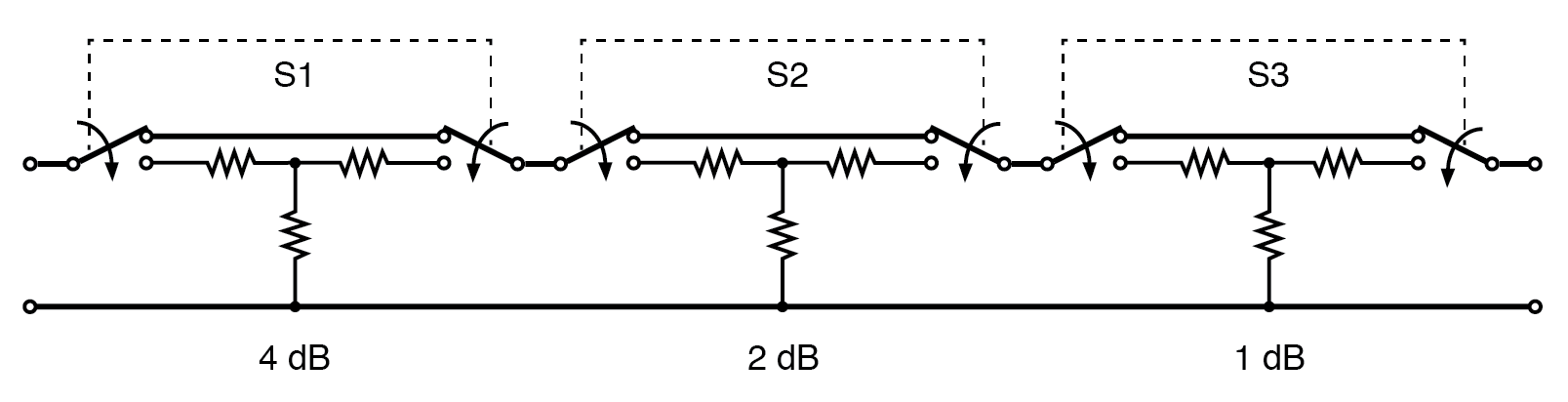
Atenuador conmutado:la atenuación es variable en pasos discretos.

El atenuador de múltiples secciones típico tiene más secciones de las que muestra la figura anterior. La adición de una sección de 3 u 8 dB por encima permite que la unidad cubra hasta 10 dB y más. Los niveles de señal más bajos se logran mediante la adición de secciones de 10 dB y 20 dB, o una sección binaria múltiple de 16 dB.

Atenuadores de RF

Para trabajos de radiofrecuencia (RF) (<1000 Mhz), las secciones individuales deben montarse en compartimentos blindados para frustrar el acoplamiento capacitivo si se quieren lograr niveles de señal más bajos en las frecuencias más altas. Las secciones individuales de los atenuadores conmutados de la sección anterior están montadas en secciones blindadas. Se pueden tomar medidas adicionales para extender el rango de frecuencia más allá de 1000 Mhz. Esto implica la construcción a partir de elementos resistivos sin plomo de forma especial.

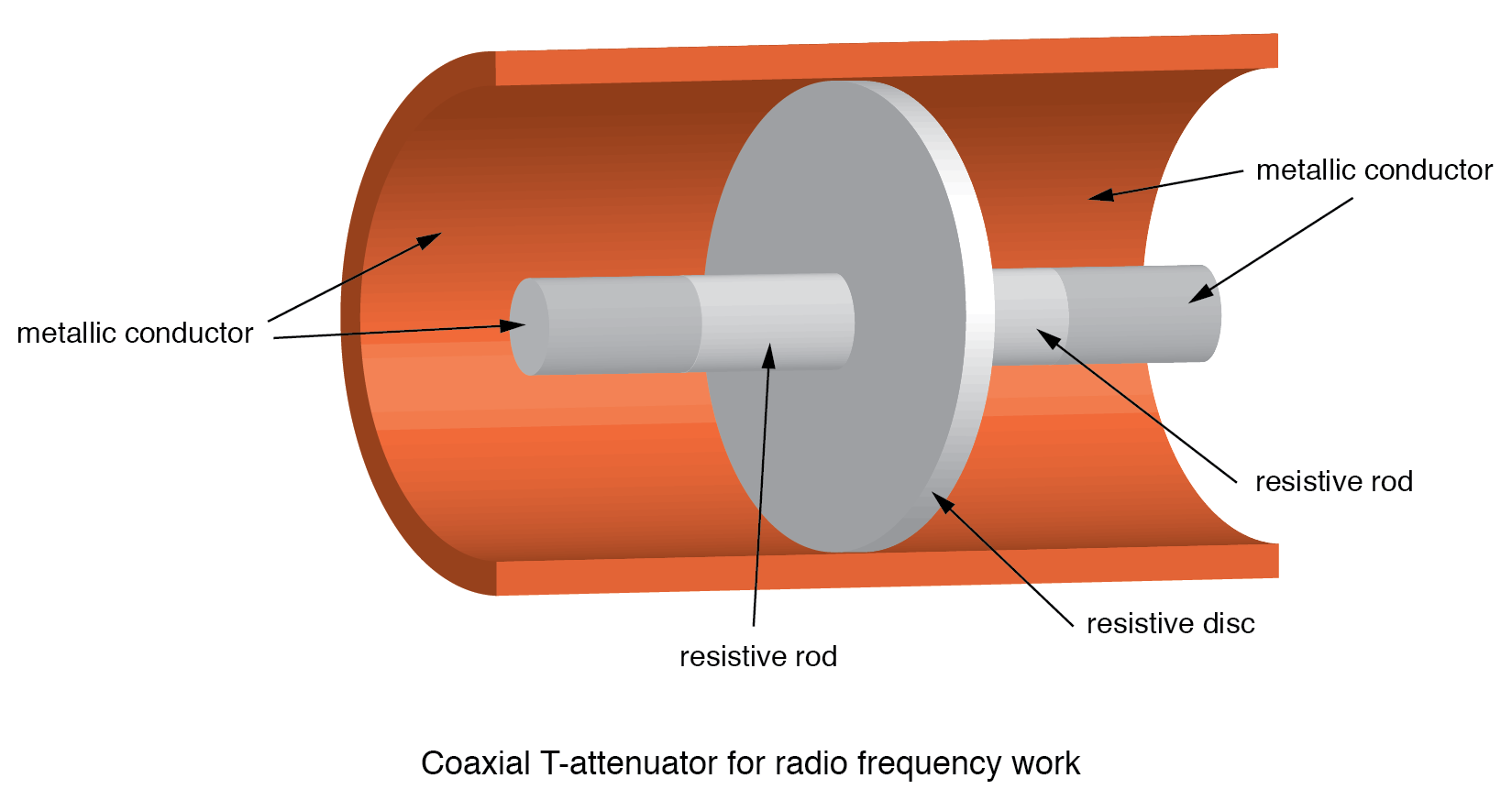
En la figura anterior se muestra un atenuador de sección en T coaxial que consta de varillas resistivas y un disco resistivo. Esta construcción se puede utilizar en unos pocos gigahercios. La versión coaxial Π tendría una varilla resistiva entre dos discos resistivos en la línea coaxial como se muestra en la siguiente figura.

Los conectores de RF, que no se muestran, están conectados a los extremos de los atenuadores T y Π anteriores. Los conectores permiten conectar en cascada atenuadores individuales, además de conectarse entre una fuente y una carga. Por ejemplo, se puede colocar un atenuador de 10 dB entre una fuente de señal problemática y una entrada costosa del analizador de espectro. Aunque no necesitemos la atenuación, el costoso equipo de prueba está protegido de la fuente atenuando cualquier sobrevoltaje.

Resumen:atenuadores

• Un atenuador reduce una señal de entrada a un nivel más bajo.
• La cantidad de atenuación se especifica en decibelios (dB). Los valores de decibelios son aditivos para las secciones del atenuador en cascada.
• dB de la relación de potencia:dB =10 log10 (PI / PO)
• dB de la relación de voltaje:dB =20 log10 (VI / VO)
• T y Π Los atenuadores de sección son las configuraciones de circuito más comunes.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de medidas de decibelios